|
Spheroid
A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has circular symmetry. If the ellipse is rotated about its major axis, the result is a ''prolate spheroid'', elongated like a rugby ball. The American football is similar but has a pointier end than a spheroid could. If the ellipse is rotated about its minor axis, the result is an ''oblate spheroid'', flattened like a lentil or a plain M&M. If the generating ellipse is a circle, the result is a sphere. Due to the combined effects of gravity and rotation, the figure of the Earth (and of all planets) is not quite a sphere, but instead is slightly flattened in the direction of its axis of rotation. For that reason, in cartography and geodesy the Earth is often approximated by an oblate spheroid, known as the reference ellipsoid, instead of a sph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spheroids
A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface (mathematics), surface obtained by Surface of revolution, rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has circular symmetry. If the ellipse is rotated about its major axis, the result is a ''prolate spheroid'', elongated like a rugby ball. The ball (gridiron football), American football is similar but has a pointier end than a spheroid could. If the ellipse is rotated about its minor axis, the result is an ''oblate spheroid'', flattened like a lentil or a plain M&M's, M&M. If the generating ellipse is a circle, the result is a sphere. Due to the combined effects of gravity and rotation of the Earth, rotation, the figure of the Earth (and of all planets) is not quite a sphere, but instead is slightly flattening, flattened in the direction of its axis of rotation. For that reason, in cartography and geod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipsoid
An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation. An ellipsoid is a quadric surface; that is, a surface that may be defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, an ellipsoid is characterized by either of the two following properties. Every planar cross section is either an ellipse, or is empty, or is reduced to a single point (this explains the name, meaning "ellipse-like"). It is bounded, which means that it may be enclosed in a sufficiently large sphere. An ellipsoid has three pairwise perpendicular axes of symmetry which intersect at a center of symmetry, called the center of the ellipsoid. The line segments that are delimited on the axes of symmetry by the ellipsoid are called the ''principal axes'', or simply axes of the ellipsoid. If the three axes have different lengths, the figure is a triaxial ellipsoid (r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
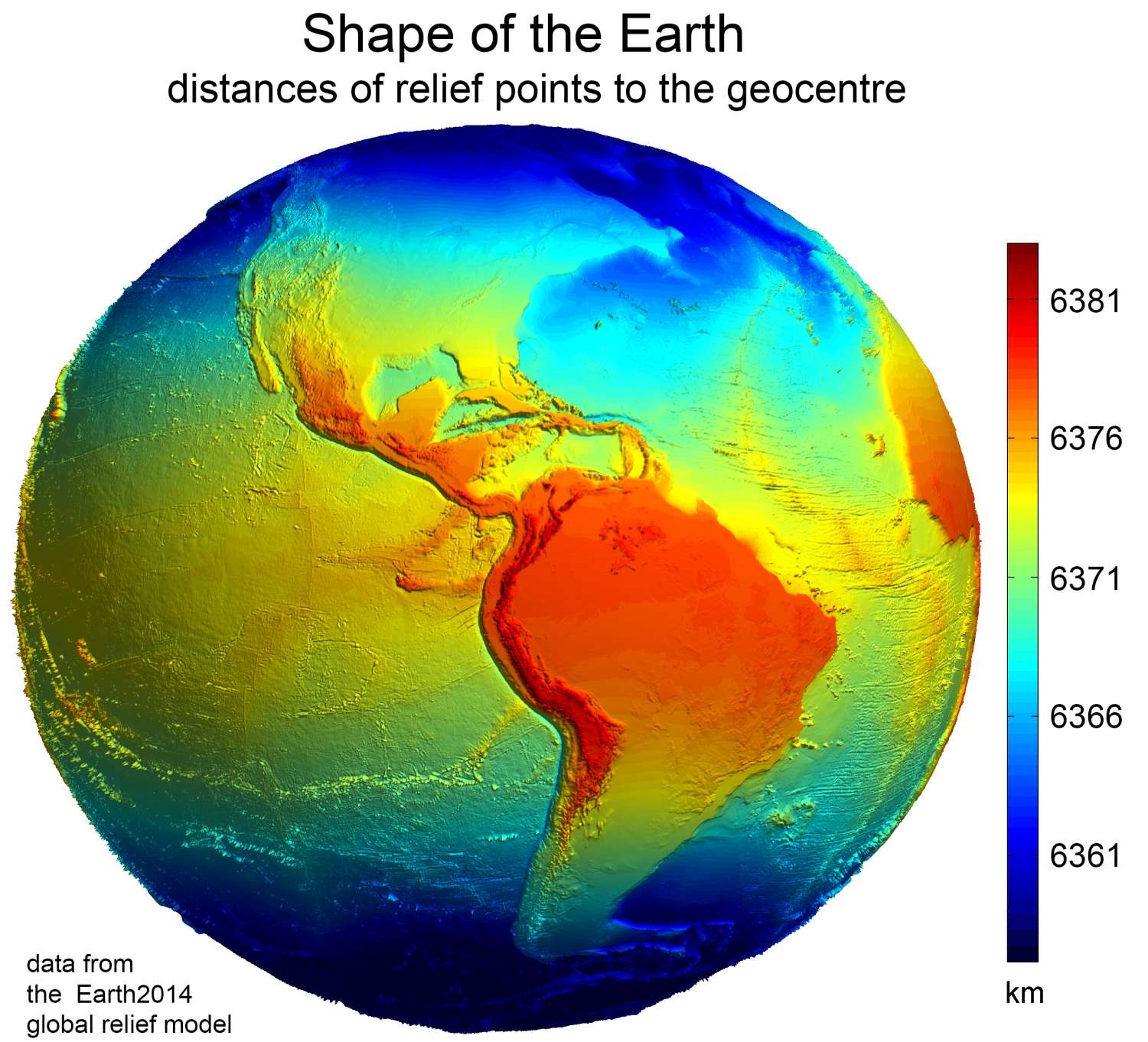Figure Of The Earth
Figure of the Earth is a Jargon, term of art in geodesy that refers to the size and shape used to model Earth. The size and shape it refers to depend on context, including the precision needed for the model. A Spherical Earth, sphere is a well-known historical approximation of the figure of the Earth that is satisfactory for many purposes. Several models with greater accuracy (including Earth ellipsoid, ellipsoid) have been developed so that Geographic coordinate system, coordinate systems can serve the precise needs of navigation, surveying, cadastre, land use, and various other concerns. Motivation Earth's Topography, topographic surface is apparent with its variety of land forms and water areas. This topographic surface is generally the concern of topographers, Hydrography, hydrographers, and Geophysics, geophysicists. While it is the surface on which Earth measurements are made, mathematically modeling it while taking the irregularities into account would be extremely compl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equator
The equator is a circle of latitude, about in circumference, that divides Earth into the Northern and Southern hemispheres. It is an imaginary line located at 0 degrees latitude, halfway between the North and South poles. The term can also be used for any other celestial body that is roughly spherical. In spatial (3D) geometry, as applied in astronomy, the equator of a rotating spheroid (such as a planet) is the parallel (circle of latitude) at which latitude is defined to be 0°. It is an imaginary line on the spheroid, equidistant from its poles, dividing it into northern and southern hemispheres. In other words, it is the intersection of the spheroid with the plane perpendicular to its axis of rotation and midway between its geographical poles. On and near the equator (on Earth), noontime sunlight appears almost directly overhead (no more than about 23° from the zenith) every day, year-round. Consequently, the equator has a rather stable daytime temperature throug ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reference Ellipsoid
An Earth ellipsoid or Earth spheroid is a mathematical figure approximating the Earth's form, used as a reference frame for computations in geodesy, astronomy, and the geosciences. Various different ellipsoids have been used as approximations. It is a spheroid (an ellipsoid of revolution) whose minor axis (shorter diameter), which connects the geographical North Pole and South Pole, is approximately aligned with the Earth's axis of rotation. The ellipsoid is defined by the ''equatorial axis'' (''a'') and the ''polar axis'' (''b''); their radial difference is slightly more than 21 km, or 0.335% of ''a'' (which is not quite 6,400 km). Many methods exist for determination of the axes of an Earth ellipsoid, ranging from meridian arcs up to modern satellite geodesy or the analysis and interconnection of continental geodetic networks. Amongst the different set of data used in national surveys are several of special importance: the Bessel ellipsoid of 1841, the international H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity (mathematics), eccentricity e, a number ranging from e = 0 (the Limiting case (mathematics), limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but only approximations for its perimeter (also known as circumference), for which integration is required to obtain an exact solution. Analytic geometry, Analytically, the equation of a standard ellipse centered at the origin with width 2a and height 2b is: : \frac+\frac = 1 . Assuming a \ge b, the foci are (\pm c, 0) for c = \sqrt. The standard parametric e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Planet
A planet is a large, rounded astronomical body that is neither a star nor its remnant. The best available theory of planet formation is the nebular hypothesis, which posits that an interstellar cloud collapses out of a nebula to create a young protostar orbited by a protoplanetary disk. Planets grow in this disk by the gradual accumulation of material driven by gravity, a process called accretion. The Solar System has at least eight planets: the terrestrial planets Mercury, Venus, Earth and Mars, and the giant planets Jupiter, Saturn, Uranus and Neptune. These planets each rotate around an axis tilted with respect to its orbital pole. All of them possess an atmosphere, although that of Mercury is tenuous, and some share such features as ice caps, seasons, volcanism, hurricanes, tectonics, and even hydrology. Apart from Venus and Mars, the Solar System planets generate magnetic fields, and all except Venus and Mercury have natural satellites. The giant planets bear plan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere
A sphere () is a Geometry, geometrical object that is a solid geometry, three-dimensional analogue to a two-dimensional circle. A sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the centre (geometry), centre of the sphere, and is the sphere's radius. The earliest known mentions of spheres appear in the work of the Greek mathematics, ancient Greek mathematicians. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubble (physics), Bubbles such as soap bubbles take a spherical shape in equilibrium. spherical Earth, The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres rolling, roll smoothly in any direction, so mos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadric
In mathematics, a quadric or quadric surface (quadric hypersurface in higher dimensions), is a generalization of conic sections (ellipses, parabolas, and hyperbolas). It is a hypersurface (of dimension ''D'') in a -dimensional space, and it is defined as the zero set of an irreducible polynomial of degree two in ''D'' + 1 variables; for example, in the case of conic sections. When the defining polynomial is not absolutely irreducible, the zero set is generally not considered a quadric, although it is often called a ''degenerate quadric'' or a ''reducible quadric''. In coordinates , the general quadric is thus defined by the algebraic equationSilvio LevQuadricsin "Geometry Formulas and Facts", excerpted from 30th Edition of ''CRC Standard Mathematical Tables and Formulas'', CRC Press, from The Geometry Center at University of Minnesota : \sum_^ x_i Q_ x_j + \sum_^ P_i x_i + R = 0 which may be compactly written in vector and matrix notation as: : x Q x^\mathrm + P x^\mathrm + ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earth's Gravity
The gravity of Earth, denoted by , is the net acceleration that is imparted to objects due to the combined effect of gravitation (from mass distribution within Earth) and the centrifugal force (from the Earth's rotation). It is a vector quantity, whose direction coincides with a plumb bob and strength or magnitude is given by the norm g=\, \mathit\, . In SI units this acceleration is expressed in metres per second squared (in symbols, m/ s2 or m·s−2) or equivalently in newtons per kilogram (N/kg or N·kg−1). Near Earth's surface, the gravity acceleration is approximately , which means that, ignoring the effects of air resistance, the speed of an object falling freely will increase by about per second every second. This quantity is sometimes referred to informally as ''little '' (in contrast, the gravitational constant is referred to as ''big ''). The precise strength of Earth's gravity varies depending on location. The nominal "average" value at Earth's surface, known ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rugby Ball
A rugby ball is an elongated ellipsoidal ball used in both codes of rugby football. Its measurements and weight are specified by World Rugby and the Rugby League International Federation, the governing bodies for both codes, rugby union and rugby league respectively. The rugby ball has an oval shape, four panels and a weight of about 400 grams. It is often confused with some balls of similar dimensions used in American, Canadian and Australian football. History William Gilbert and Richard Lindon started making footballs for the neighbouring Rugby School in 1823. The balls had an inner-tube made of a pig's bladder. Both men owned boot and shoe making businesses located close to Rugby school.The pioneers on Rugby Football History In 1870, |
Ball (gridiron Football)
In Canada and the United States, a football (also called a pigskin) is a ball, roughly in the form of a prolate spheroid, used in the context of playing gridiron football. Footballs are often made of cowhide leather, as such a material is required in professional and collegiate football. Footballs used in recreation, and in organized youth leagues, may be made of rubber, plastic or composite leather (high school football rule books still allow inexpensive all-rubber footballs, though they are less common than leather). History Early balls In the 1860s, manufactured inflatable balls were introduced through the innovations of English shoemaker Richard Lindon. These were much more regular in shape than the handmade balls of earlier times, making kicking and carrying easier. These early footballs were plum-shaped. Some teams used to have white footballs for purposes of night practice. The football changed in 1934, with a rule change that tapered the ball at the ends more and redu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
