|
Circle Of A Sphere
In spherical geometry, a spherical circle (often shortened to circle) is the locus of points on a sphere at constant spherical distance (the ''spherical radius'') from a given point on the sphere (the ''pole'' or ''spherical center''). It is a curve of constant geodesic curvature relative to the sphere, analogous to a line or circle in the Euclidean plane; the curves analogous to straight lines are called ''great circles'', and the curves analogous to planar circles are called small circles or lesser circles. If the sphere is embedded in three-dimensional Euclidean space, its circles are the intersections of the sphere with planes, and the great circles are intersections with planes passing through the center of the sphere. Fundamental concepts Intrinsic characterization A spherical circle with zero geodesic curvature is called a ''great circle'', and is a geodesic analogous to a straight line in the plane. A great circle separates the sphere into two equal '' hem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Geodesic
In geometry, a geodesic () is a curve representing in some sense the locally shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a " straight line". The noun '' geodesic'' and the adjective '' geodetic'' come from ''geodesy'', the science of measuring the size and shape of Earth, though many of the underlying principles can be applied to any ellipsoidal geometry. In the original sense, a geodesic was the shortest route between two points on the Earth's surface. For a spherical Earth, it is a segment of a great circle (see also great-circle distance). The term has since been generalized to more abstract mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph. In a Riemannian manifold or submanifold, geodesics are characterised by the property of havi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Right Circular Cylinder
A right circular cylinder is a cylinder whose generatrices are perpendicular to the bases. Thus, in a right circular cylinder, the generatrix and the height have the same measurements. It is also less often called a cylinder of revolution, because it can be obtained by rotating a rectangle of sides r and g around one of its sides. Fixing g as the side on which the revolution takes place, we obtain that the side r, perpendicular to g, will be the measure of the radius of the cylinder. In addition to the right circular cylinder, within the study of spatial geometry there is also the '' oblique circular cylinder'', characterized by not having the geratrices perpendicular to the bases. Elements of the right circular cylinder Bases: the two parallel and congruent circles of the bases; Axis: the line determined by the two points of the centers of the cylinder's bases; Height: the distance between the two planes of the cylinder's bases; Generatrices: the line segments parallel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
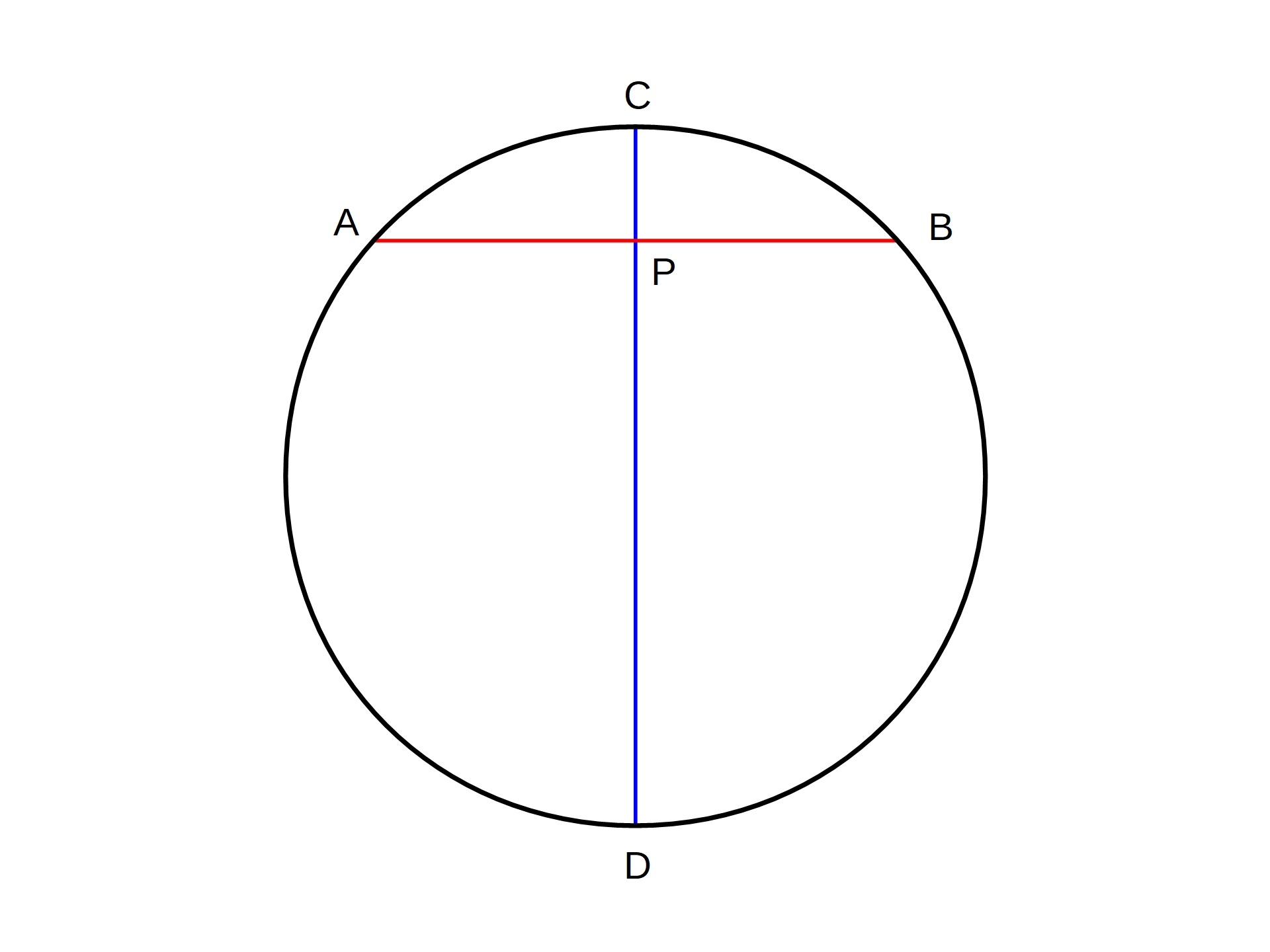
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest Chord (geometry), chord of the circle. Both definitions are also valid for the diameter of a sphere. In more modern usage, the length d of a diameter is also called the diameter. In this sense one speaks of diameter rather than diameter (which refers to the line segment itself), because all diameters of a circle or sphere have the same length, this being twice the radius r. :d = 2r \qquad\text\qquad r = \frac. The word "diameter" is derived from (), "diameter of a circle", from (), "across, through" and (), "measure". It is often abbreviated \text, \text, d, or \varnothing. Constructions With straightedge and compass, a diameter of a given circle can be constructed as the perpendicular bisector of an arbitrary chord. Drawing two diameters in this way can be used to locate the center of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Euclidean Distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is occasionally called the Pythagorean distance. These names come from the ancient Greek mathematicians Euclid and Pythagoras. In the Greek deductive geometry exemplified by Euclid's ''Elements'', distances were not represented as numbers but line segments of the same length, which were considered "equal". The notion of distance is inherent in the compass tool used to draw a circle, whose points all have the same distance from a common center point. The connection from the Pythagorean theorem to distance calculation was not made until the 18th century. The distance between two objects that are not points is usually defined to be the smallest distance among pairs of points from the two objects. Formulas are known for computing distances b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Embedding
In mathematics, an embedding (or imbedding) is one instance of some mathematical structure contained within another instance, such as a group (mathematics), group that is a subgroup. When some object X is said to be embedded in another object Y, the embedding is given by some Injective function, injective and structure-preserving map f:X\rightarrow Y. The precise meaning of "structure-preserving" depends on the kind of mathematical structure of which X and Y are instances. In the terminology of category theory, a structure-preserving map is called a morphism. The fact that a map f:X\rightarrow Y is an embedding is often indicated by the use of a "hooked arrow" (); thus: f : X \hookrightarrow Y. (On the other hand, this notation is sometimes reserved for inclusion maps.) Given X and Y, several different embeddings of X in Y may be possible. In many cases of interest there is a standard (or "canonical") embedding, like those of the natural numbers in the integers, the integers i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Isometry
In mathematics, an isometry (or congruence, or congruent transformation) is a distance-preserving transformation between metric spaces, usually assumed to be bijective. The word isometry is derived from the Ancient Greek: ἴσος ''isos'' meaning "equal", and μέτρον ''metron'' meaning "measure". If the transformation is from a metric space to itself, it is a kind of geometric transformation known as a motion. Introduction Given a metric space (loosely, a set and a scheme for assigning distances between elements of the set), an isometry is a transformation which maps elements to the same or another metric space such that the distance between the image elements in the new metric space is equal to the distance between the elements in the original metric space. In a two-dimensional or three-dimensional Euclidean space, two geometric figures are congruent if they are related by an isometry; the isometry that relates them is either a rigid motion (translation or rotati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Parallel Line
Parallel may refer to: Mathematics * Parallel (geometry), two lines in the Euclidean plane which never intersect * Parallel (operator), mathematical operation named after the composition of electrical resistance in parallel circuits Science and engineering * Parallel (latitude), an imaginary east–west line circling a globe * Parallel of declination, used in astronomy * Parallel, a geometric term of location meaning "in the same direction" * Parallel electrical circuits Computing * Parallel (software), a UNIX utility for running programs in parallel Language * Parallelism (grammar), a balance of two or more similar words, phrases, or clauses * Parallelism (rhetoric) Entertainment * ''Parallel'' (manga) * ''Parallel'' (2018 film), a Canadian science fiction thriller film * ''Parallel'' (2024 film) an American science fiction thriller film * ''Parallel'' (video), a compilation of music videos by R.E.M. * ''Parallel'' (The Black Dog album), 1995 * ''Parallel'' (F ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Concentric
In geometry, two or more objects are said to be ''concentric'' when they share the same center. Any pair of (possibly unalike) objects with well-defined centers can be concentric, including circles, spheres, regular polygons, regular polyhedra, parallelograms, cones, conic sections, and quadrics. Geometric objects are '' coaxial'' if they share the same axis (line of symmetry). Geometric objects with a well-defined axis include circles (any line through the center), spheres, cylinders, conic sections, and surfaces of revolution. Concentric objects are often part of the broad category of '' whorled patterns'', which also includes '' spirals'' (a curve which emanates from a point, moving farther away as it revolves around the point). Geometric properties In the Euclidean plane, two circles that are concentric necessarily have different radii from each other.. However, circles in three-dimensional space may be concentric, and have the same radius as each other, but nevert ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Circular Arc
A circular arc is the arc of a circle between a pair of distinct points. If the two points are not directly opposite each other, one of these arcs, the minor arc, subtends an angle at the center of the circle that is less than radians (180 degrees); and the other arc, the major arc, subtends an angle greater than radians. The arc of a circle is defined as the part or segment of the circumference of a circle. A straight line that connects the two ends of the arc is known as a '' chord'' of a circle. If the length of an arc is exactly half of the circle, it is known as a '' semicircular arc''. Length The length (more precisely, arc length) of an arc of a circle with radius ''r'' and subtending an angle ''θ'' (measured in radians) with the circle center — i.e., the central angle — is : L = \theta r. This is because :\frac=\frac. Substituting in the circumference :\frac=\frac, and, with ''α'' being the same angle measured in degrees, since ''θ'' = , the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Spherical Cap
In geometry, a spherical cap or spherical dome is a portion of a sphere or of a ball (mathematics), ball cut off by a plane (mathematics), plane. It is also a spherical segment of one base, i.e., bounded by a single plane. If the plane passes through the center (geometry), center of the sphere (forming a great circle), so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a ''Sphere#Hemisphere, hemisphere''. Volume and surface area The volume of the spherical cap and the area of the curved surface may be calculated using combinations of * The radius r of the sphere * The radius a of the base of the cap * The height h of the cap * The Spherical coordinate system, polar angle \theta between the rays from the center of the sphere to the apex of the cap (the pole) and the edge of the disk (mathematics), disk forming the base of the cap. These variables are inter-related through the formulas a = r \sin \theta, h = r ( 1 - \cos \theta ), 2hr = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |