Line–sphere Intersection

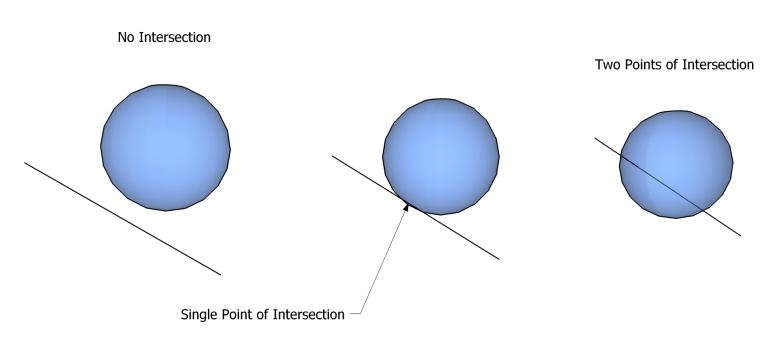
In analytic geometry, a line and a sphere can intersect in three ways:

# No intersection at all
# Intersection in exactly one point
# Intersection in two points.

Methods for distinguishing these cases, and determining the coordinates for the points in the latter cases, are useful in a number of circumstances. For example, it is a common calculation to perform during ray tracing.

Calculation using vectors in 3D

In vector notation, the equations are as follows:

Equation for a sphere
:$\left\Vert \mathbf - \mathbf \right\Vert^2=r^2$
:*$\mathbf$ : points on the sphere
:*$\mathbf$ : center point
:*$r$ : radius of the sphere

Equation for a line starting at $\mathbf$
:$\mathbf=\mathbf + d\mathbf$
:*$\mathbf$ : points on the line
:*$\mathbf$ : origin of the line
:*$d$ : distance from the origin of the line
:*$\mathbf$ : direction of line (a non-zero vector)

Searching for points that are on the line and on the sphere means combining the equations and solving for $d$, involving the dot product of vectors:

:Equations combined
::$\left\Vert \mathbf + d\mathbf - \mathbf \right\Vert^2=r^2 \Leftrightarrow (\mathbf + d\mathbf - \mathbf) \cdot (\mathbf + d\mathbf - \mathbf) = r^2$
:Expanded and rearranged:
::d^2(\mathbf\cdot\mathbf)+2d mathbf\cdot(\mathbf-\mathbf)(\mathbf-\mathbf)\cdot(\mathbf-\mathbf)-r^2=0
:The form of a quadratic formula is now observable. (This quadratic equation is an instance of Joachimsthal's equation.)
::$a d^2 + b d + c = 0$
:where
:*$a=\mathbf\cdot\mathbf=\left\Vert\mathbf\right\Vert^2$
:*b=2 mathbf\cdot(\mathbf-\mathbf)/math>
:*$c=(\mathbf-\mathbf)\cdot(\mathbf-\mathbf)-r^2=\left\Vert\mathbf-\mathbf\right\Vert^2-r^2$
:Simplified
::$d = \frac$
:Note that in the specific case where $\mathbf$ is a unit vector, and thus $\left\Vert\mathbf\right\Vert^2=1$, we can simplify this further to (writing $\hat$ instead of $\mathbf$ to indicate a unit vector):
::\nabla= hat\cdot(\mathbf-\mathbf)2-(\left\Vert\mathbf-\mathbf\right\Vert^2-r^2)
::d=- hat\cdot(\mathbf-\mathbf)\pm \sqrt

:*If $\nabla < 0$, then it is clear that no solutions exist, i.e. the line does not intersect the sphere (case 1).
:*If $\nabla = 0$, then exactly one solution exists, i.e. the line just touches the sphere in one point (case 2).
:*If $\nabla > 0$, two solutions exist, and thus the line touches the sphere in two points (case 3).

See also

*
*Analytic geometry
* Line–plane intersection
* Plane–plane intersection
* Plane–sphere intersection

References

{{DEFAULTSORT:Line-sphere intersection
Analytic geometry
Geometric algorithms
Geometric intersection
Spherical geometry