General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the
geometric
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is ca ...
theory
A theory is a rational type of abstract thinking about a phenomenon, or the results of such thinking. The process of contemplative and rational thinking is often associated with such processes as observational study or research. Theories may ...
of
gravitation published by
Albert Einstein
Albert Einstein ( ; ; 14 March 1879 – 18 April 1955) was a German-born theoretical physicist, widely acknowledged to be one of the greatest and most influential physicists of all time. Einstein is best known for developing the theor ...
in 1915 and is the current description of gravitation in
modern physics. General
relativity generalizes
special relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory regarding the relationship between space and time. In Albert Einstein's original treatment, the theory is based on two postulates:
# The law ...
and refines
Newton's law of universal gravitation
Newton's law of universal gravitation is usually stated as that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distanc ...
, providing a unified description of gravity as a geometric property of
space
Space is the boundless three-dimensional extent in which objects and events have relative position and direction. In classical physics, physical space is often conceived in three linear dimensions, although modern physicists usually con ...
and
time
Time is the continued sequence of existence and events that occurs in an apparently irreversible succession from the past, through the present, into the future. It is a component quantity of various measurements used to sequence events, t ...
or
four-dimensional
A four-dimensional space (4D) is a mathematical extension of the concept of three-dimensional or 3D space. Three-dimensional space is the simplest possible abstraction of the observation that one only needs three numbers, called ''dimensions'', ...
spacetime
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why diffe ...
. In particular, the ' is directly related to the
energy
In physics, energy (from Ancient Greek: ἐνέργεια, ''enérgeia'', “activity”) is the quantitative property that is transferred to a body or to a physical system, recognizable in the performance of work and in the form of hea ...
and
momentum
In Newtonian mechanics, momentum (more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass ...
of whatever
matter
In classical physics and general chemistry, matter is any substance that has mass and takes up space by having volume. All everyday objects that can be touched are ultimately composed of atoms, which are made up of interacting subatomic par ...
and
radiation
In physics, radiation is the emission or transmission of energy in the form of waves or particles through space or through a material medium. This includes:
* ''electromagnetic radiation'', such as radio waves, microwaves, infrared, vi ...
are present. The relation is specified by the
Einstein field equations
In the general theory of relativity, the Einstein field equations (EFE; also known as Einstein's equations) relate the geometry of spacetime to the distribution of matter within it.
The equations were published by Einstein in 1915 in the form ...
, a system of second order
partial differential equation
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function.
The function is often thought of as an "unknown" to be solved for, similarly to ...
s.
Newton's law of universal gravitation
Newton's law of universal gravitation is usually stated as that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distanc ...
, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond
Newton's law of universal gravitation
Newton's law of universal gravitation is usually stated as that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distanc ...
in
classical physics. These predictions concern the passage of time, the
geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
of space, the motion of bodies in
free fall
In Newtonian physics, free fall is any motion of a body where gravity is the only force acting upon it. In the context of general relativity, where gravitation is reduced to a space-time curvature, a body in free fall has no force acting on i ...
, and the propagation of light, and include
gravitational time dilation
Gravitational time dilation is a form of time dilation, an actual difference of elapsed time between two events as measured by observers situated at varying distances from a gravitating mass. The lower the gravitational potential (the close ...
,
gravitational lens
A gravitational lens is a distribution of matter (such as a cluster of galaxies) between a distant light source and an observer that is capable of bending the light from the source as the light travels toward the observer. This effect is known ...
ing, the
gravitational redshift
In physics and general relativity, gravitational redshift (known as Einstein shift in older literature) is the phenomenon that electromagnetic waves or photons travelling out of a gravitational well (seem to) lose energy. This loss of energy ...
of light, the
Shapiro time delay
The Shapiro time delay effect, or gravitational time delay effect, is one of the four classic solar-system tests of general relativity. Radar signals passing near a massive object take slightly longer to travel to a target and longer to return tha ...
and
singularities/
black holes
A black hole is a region of spacetime where gravity is so strong that nothing, including light or other electromagnetic waves, has enough energy to escape it. The theory of general relativity predicts that a sufficiently compact mass can defo ...
. So far, all
tests of general relativity
Tests of general relativity serve to establish observational evidence for the theory of general relativity. The first three tests, proposed by Albert Einstein in 1915, concerned the "anomalous" precession of the perihelion of Mercury (planet), Me ...
have been shown to be in agreement with the theory. The time dependent solutions of general relativity enable us to talk about the history of the universe and have provided the modern framework for
cosmology
Cosmology () is a branch of physics and metaphysics dealing with the nature of the universe. The term ''cosmology'' was first used in English in 1656 in Thomas Blount's ''Glossographia'', and in 1731 taken up in Latin by German philosophe ...
, thus leading to the discovery of the
Big Bang
The Big Bang event is a physical theory that describes how the universe expanded from an initial state of high density and temperature. Various cosmological models of the Big Bang explain the evolution of the observable universe from t ...
and
cosmic microwave background
In Big Bang cosmology the cosmic microwave background (CMB, CMBR) is electromagnetic radiation that is a remnant from an early stage of the universe, also known as "relic radiation". The CMB is faint cosmic background radiation filling all spac ...
radiation. Despite the introduction of a number of
alternative theories, general relativity continues to be the simplest theory consistent with
experimental data
Experimental data in science and engineering is data produced by a measurement, test method, experimental design or quasi-experimental design. In clinical research any data produced are the result of a clinical trial. Experimental data may be qu ...
.
Reconciliation of general relativity with the laws of
quantum physics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, q ...
remains a problem, however, as there is a lack of a self-consistent theory of
quantum gravity
Quantum gravity (QG) is a field of theoretical physics that seeks to describe gravity according to the principles of quantum mechanics; it deals with environments in which neither gravitational nor quantum effects can be ignored, such as in the v ...
. It is not yet known how gravity can be
unified with the three non-gravitational forces:
strong,
weak and
electromagnetic
In physics, electromagnetism is an interaction that occurs between particles with electric charge. It is the second-strongest of the four fundamental interactions, after the strong force, and it is the dominant force in the interactions of a ...
.
Einstein's theory has
astrophysical
Astrophysics is a science that employs the methods and principles of physics and chemistry in the study of astronomical objects and phenomena. As one of the founders of the discipline said, Astrophysics "seeks to ascertain the nature of the he ...
implications, including the prediction of
black holes
A black hole is a region of spacetime where gravity is so strong that nothing, including light or other electromagnetic waves, has enough energy to escape it. The theory of general relativity predicts that a sufficiently compact mass can defo ...
—regions of space in which space and time are distorted in such a way that nothing, not even
light
Light or visible light is electromagnetic radiation that can be perceived by the human eye. Visible light is usually defined as having wavelengths in the range of 400–700 nanometres (nm), corresponding to frequencies of 750–420 te ...
, can escape from them. Black holes are the end-state for
massive star
A star is an astronomical object comprising a luminous spheroid of plasma held together by its gravity. The nearest star to Earth is the Sun. Many other stars are visible to the naked eye at night, but their immense distances from Earth mak ...
s.
Microquasar
A microquasar, the smaller version of a quasar, is a compact region surrounding a stellar black hole with a mass several times that of its companion star. The matter being pulled from the companion star forms an accretion disk around the black h ...
s and
active galactic nuclei
An active galactic nucleus (AGN) is a compact region at the center of a galaxy that has a much-higher-than-normal luminosity over at least some portion of the electromagnetic spectrum with characteristics indicating that the luminosity is not prod ...
are believed to be
stellar black hole
A stellar black hole (or stellar-mass black hole) is a black hole formed by the gravitational collapse of a star. They have masses ranging from about 5 to several tens of solar masses. The process is observed as a hypernova explosion or as a ga ...
s and
supermassive black hole
A supermassive black hole (SMBH or sometimes SBH) is the largest type of black hole, with its mass being on the order of hundreds of thousands, or millions to billions of times the mass of the Sun (). Black holes are a class of astronomical obj ...
s. It also predicts
gravitational lensing
A gravitational lens is a distribution of matter (such as a cluster of galaxies) between a distant light source and an observer that is capable of bending the light from the source as the light travels toward the observer. This effect is known ...
, where the bending of light results in multiple images of the same distant astronomical phenomenon. Other predictions include the existence of
gravitational wave
Gravitational waves are waves of the intensity of gravity generated by the accelerated masses of an orbital binary system that propagate as waves outward from their source at the speed of light. They were first proposed by Oliver Heaviside in ...
s, which have been
observed directly by the physics collaboration
LIGO
The Laser Interferometer Gravitational-Wave Observatory (LIGO) is a large-scale physics experiment and observatory designed to detect cosmic gravitational waves and to develop gravitational-wave observations as an astronomical tool. Two large o ...
and other observatories. In addition, general relativity has provided the base of
cosmological
Cosmology () is a branch of physics and metaphysics dealing with the nature of the universe. The term ''cosmology'' was first used in English in 1656 in Thomas Blount's ''Glossographia'', and in 1731 taken up in Latin by German philosopher ...
models of an
expanding universe
The expansion of the universe is the increase in distance between any two given gravitationally unbound parts of the observable universe with time. It is an intrinsic expansion whereby the scale of space itself changes. The universe does not ...
.
In the preface to
Relativity: The Special and the General Theory, Einstein said "The present book is intended, as far as possible, to give an exact insight into the theory of Relativity to those readers who, from a general scientific and philosophical point of view, are interested in the theory, but who are not conversant with the mathematical apparatus of theoretical physics. The work presumes a standard of education corresponding to that of a university matriculation examination, and, despite the shortness of the book, a fair amount of patience and force of will on the part of the reader. The author has spared himself no pains in his endeavour to present the main ideas in the simplest and most intelligible form, and on the whole, in the sequence and connection in which they actually originated."
Widely acknowledged as a theory of extraordinary
beauty
Beauty is commonly described as a feature of objects that makes these objects pleasurable to perceive. Such objects include landscapes, sunsets, humans and works of art. Beauty, together with art and taste, is the main subject of aesthetics, o ...
, general relativity has often been described as the most beautiful of all existing physical theories.
History
Soon after publishing the
special theory of relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory regarding the relationship between space and time. In Albert Einstein's original treatment, the theory is based on two postulates:
# The laws o ...
in 1905, Einstein started thinking about how to incorporate
gravity
In physics, gravity () is a fundamental interaction which causes mutual attraction between all things with mass or energy. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the str ...
into his new relativistic framework. In 1907, beginning with a simple
thought experiment
A thought experiment is a hypothetical situation in which a hypothesis, theory, or principle is laid out for the purpose of thinking through its consequences.
History
The ancient Greek ''deiknymi'' (), or thought experiment, "was the most anci ...
involving an observer in free fall, he embarked on what would be an eight-year search for a relativistic theory of gravity. After numerous detours and false starts, his work culminated in the presentation to the
Prussian Academy of Science in November 1915 of what are now known as the Einstein field equations, which form the core of Einstein's general theory of relativity. These equations specify how the geometry of space and time is influenced by whatever matter and radiation are present. A version of
non-Euclidean geometry
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean ...
, called
Riemannian Geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a ''Riemannian metric'', i.e. with an inner product on the tangent space at each point that varies smoothly from point to po ...
, enabled Einstein to develop general relativity by providing the key mathematical framework on which he fit his physical ideas of gravity. This idea was pointed out by mathematician
Marcel Grossmann
Marcel Grossmann (April 9, 1878 – September 7, 1936) was a Swiss mathematician and a friend and classmate of Albert Einstein. Grossmann was a member of an old Swiss family from Zurich. His father managed a textile factory. He became a Profe ...
and published by Grossmann and Einstein in 1913.
The Einstein field equations are
nonlinear
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other ...
and considered difficult to solve. Einstein used approximation methods in working out initial predictions of the theory. But in 1916, the astrophysicist
Karl Schwarzschild
Karl Schwarzschild (; 9 October 1873 – 11 May 1916) was a German physicist and astronomer.
Schwarzschild provided the first exact solution to the Einstein field equations of general relativity, for the limited case of a single spherical non-r ...
found the first non-trivial exact solution to the Einstein field equations, the
Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild metric (also known as the Schwarzschild solution) is an
exact solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assump ...
. This solution laid the groundwork for the description of the final stages of gravitational collapse, and the objects known today as black holes. In the same year, the first steps towards generalizing Schwarzschild's solution to
electrically charged objects were taken, eventually resulting in the
Reissner–Nordström solution, which is now associated with
electrically charged black holes. In 1917, Einstein applied his theory to the
universe
The universe is all of space and time and their contents, including planets, stars, galaxies, and all other forms of matter and energy. The Big Bang theory is the prevailing cosmological description of the development of the universe. A ...
as a whole, initiating the field of relativistic cosmology. In line with contemporary thinking, he assumed a static universe, adding a new parameter to his original field equations—the
cosmological constant
In cosmology, the cosmological constant (usually denoted by the Greek capital letter lambda: ), alternatively called Einstein's cosmological constant,
is the constant coefficient of a term that Albert Einstein temporarily added to his field eq ...
—to match that observational presumption. By 1929, however, the work of
Hubble and others had shown that our universe is expanding. This is readily described by the expanding cosmological solutions found by
Friedmann in 1922, which do not require a cosmological constant.
Lemaître used these solutions to formulate the earliest version of the
Big Bang
The Big Bang event is a physical theory that describes how the universe expanded from an initial state of high density and temperature. Various cosmological models of the Big Bang explain the evolution of the observable universe from t ...
models, in which our universe has evolved from an extremely hot and dense earlier state. Einstein later declared the cosmological constant the biggest blunder of his life.
During that period, general relativity remained something of a curiosity among physical theories. It was clearly superior to
Newtonian gravity
Newton's law of universal gravitation is usually stated as that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distanc ...
, being consistent with special relativity and accounting for several effects unexplained by the Newtonian theory. Einstein showed in 1915 how his theory explained the
anomalous perihelion advance of the planet
Mercury without any arbitrary parameters ("
fudge factors"), and in 1919 an expedition led by
Eddington Eddington or Edington may refer to:
People
* Eddington Varmah, Liberian politician
* Eddington (surname), people with the surname
Places
Australia
* Eddington, Victoria
United Kingdom
* Eddington, Berkshire
* Eddington, Cambridge
* E ...
confirmed general relativity's prediction for the deflection of starlight by the Sun during the total
solar eclipse of 29 May 1919
A total solar eclipse occurred on Thursday, May 29, 1919. With the duration of totality at maximum eclipse of 6 minutes 50.75 seconds, it was the longest solar eclipse since May 27, 1416. A longer total solar eclipse would later occur on June 8 ...
, instantly making Einstein famous. Yet the theory remained outside the mainstream of
theoretical physics
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain and predict natural phenomena. This is in contrast to experimental physics, which uses experi ...
and astrophysics until developments between approximately 1960 and 1975, now known as the
golden age of general relativity. Physicists began to understand the concept of a black hole, and to identify
quasar
A quasar is an extremely luminous active galactic nucleus (AGN). It is pronounced , and sometimes known as a quasi-stellar object, abbreviated QSO. This emission from a galaxy nucleus is powered by a supermassive black hole with a mass rangin ...
s as one of these objects' astrophysical manifestations. Ever more precise solar system tests confirmed the theory's predictive power, and relativistic cosmology also became amenable to direct observational tests.
General relativity has acquired a reputation as a theory of extraordinary beauty.
[ "...the ''general theory of relativity''...was established by Einstein, and represents probably the most beautiful of all existing physical theories."] Subrahmanyan Chandrasekhar
Subrahmanyan Chandrasekhar (; ) (19 October 1910 – 21 August 1995) was an Indian-American theoretical physicist who spent his professional life in the United States. He shared the 1983 Nobel Prize for Physics with William A. Fowler for ".. ...
has noted that at multiple levels, general relativity exhibits what
Francis Bacon
Francis Bacon, 1st Viscount St Alban (; 22 January 1561 – 9 April 1626), also known as Lord Verulam, was an English philosopher and statesman who served as Attorney General and Lord Chancellor of England. Bacon led the advancement of both ...
has termed a "strangeness in the proportion" (''i.e''. elements that excite wonderment and surprise). It juxtaposes fundamental concepts (space and time ''versus'' matter and motion) which had previously been considered as entirely independent. Chandrasekhar also noted that Einstein's only guides in his search for an exact theory were the principle of equivalence and his sense that a proper description of gravity should be geometrical at its basis, so that there was an "element of revelation" in the manner in which Einstein arrived at his theory. Other elements of beauty associated with the general theory of relativity are its simplicity and symmetry, the manner in which it incorporates invariance and unification, and its perfect logical consistency.
From classical mechanics to general relativity
General relativity can be understood by examining its similarities with and departures from classical physics. The first step is the realization that classical mechanics and Newton's law of gravity admit a geometric description. The combination of this description with the laws of special relativity results in a heuristic derivation of general relativity.
Geometry of Newtonian gravity

At the base of
classical mechanics
Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classical ...
is the notion that a
body
Body may refer to:
In science
* Physical body, an object in physics that represents a large amount, has mass or takes up space
* Body (biology), the physical material of an organism
* Body plan, the physical features shared by a group of anima ...
's motion can be described as a combination of free (or
inertia
Inertia is the idea that an object will continue its current motion until some force causes its speed or direction to change. The term is properly understood as shorthand for "the principle of inertia" as described by Newton in his first law o ...
l) motion, and deviations from this free motion. Such deviations are caused by external forces acting on a body in accordance with Newton's second
law of motion, which states that the net
force
In physics, a force is an influence that can change the motion of an object. A force can cause an object with mass to change its velocity (e.g. moving from a state of rest), i.e., to accelerate. Force can also be described intuitively as a ...
acting on a body is equal to that body's (inertial)
mass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different element ...
multiplied by its
acceleration
In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Accelerations are vector quantities (in that they have magnitude and direction). The orientation of an object's acceleration is given by ...
. The preferred inertial motions are related to the geometry of space and time: in the standard
reference frames
In physics and astronomy, a frame of reference (or reference frame) is an abstract coordinate system whose origin, orientation, and scale are specified by a set of reference points― geometric points whose position is identified both mathem ...
of classical mechanics, objects in free motion move along straight lines at constant speed. In modern parlance, their paths are
geodesic
In geometry, a geodesic () is a curve representing in some sense the shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. ...
s, straight
world lines in curved spacetime.
Conversely, one might expect that inertial motions, once identified by observing the actual motions of bodies and making allowances for the external forces (such as
electromagnetism
In physics, electromagnetism is an interaction that occurs between particles with electric charge. It is the second-strongest of the four fundamental interactions, after the strong force, and it is the dominant force in the interactions o ...
or
friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding (motion), sliding against each other. There are several types of friction:
*Dry friction is a force that opposes the relative la ...
), can be used to define the geometry of space, as well as a time
coordinate
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is si ...
. However, there is an ambiguity once gravity comes into play. According to Newton's law of gravity, and independently verified by experiments such as that of
Eötvös and its successors (see
Eötvös experiment), there is a universality of free fall (also known as the weak
equivalence principle, or the universal equality of inertial and passive-gravitational mass): the trajectory of a
test body in free fall depends only on its position and initial speed, but not on any of its material properties. A simplified version of this is embodied in Einstein's elevator experiment, illustrated in the figure on the right: for an observer in an enclosed room, it is impossible to decide, by mapping the trajectory of bodies such as a dropped ball, whether the room is stationary in a gravitational field and the ball accelerating, or in free space aboard a rocket that is accelerating at a rate equal to that of the gravitational field versus the ball which upon release has nil acceleration.
Given the universality of free fall, there is no observable distinction between inertial motion and motion under the influence of the gravitational force. This suggests the definition of a new class of inertial motion, namely that of objects in free fall under the influence of gravity. This new class of preferred motions, too, defines a geometry of space and time—in mathematical terms, it is the geodesic motion associated with a specific
connection which depends on the
gradient
In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p is the "direction and rate of fastest increase". If the gr ...
of the
gravitational potential
In classical mechanics, the gravitational potential at a location is equal to the work ( energy transferred) per unit mass that would be needed to move an object to that location from a fixed reference location. It is analogous to the electr ...
. Space, in this construction, still has the ordinary
Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry: the ''Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms ...
. However, space''time'' as a whole is more complicated. As can be shown using simple thought experiments following the free-fall trajectories of different test particles, the result of transporting spacetime vectors that can denote a particle's velocity (time-like vectors) will vary with the particle's trajectory; mathematically speaking, the Newtonian connection is not
integrable. From this, one can deduce that spacetime is curved. The resulting
Newton–Cartan theory is a geometric formulation of Newtonian gravity using only
covariant concepts, i.e. a description which is valid in any desired coordinate system. In this geometric description,
tidal effects—the relative acceleration of bodies in free fall—are related to the derivative of the connection, showing how the modified geometry is caused by the presence of mass.
Relativistic generalization

As intriguing as geometric Newtonian gravity may be, its basis, classical mechanics, is merely a
limiting case of (special) relativistic mechanics. In the language of
symmetry: where gravity can be neglected, physics is
Lorentz invariant
In a relativistic theory of physics, a Lorentz scalar is an expression, formed from items of the theory, which evaluates to a scalar, invariant under any Lorentz transformation. A Lorentz scalar may be generated from e.g., the scalar product of ...
as in special relativity rather than
Galilei invariant as in classical mechanics. (The defining symmetry of special relativity is the
Poincaré group
The Poincaré group, named after Henri Poincaré (1906), was first defined by Hermann Minkowski (1908) as the group of Minkowski spacetime isometries. It is a ten-dimensional non-abelian Lie group that is of importance as a model in our und ...
, which includes translations, rotations, boosts and reflections.) The differences between the two become significant when dealing with speeds approaching the
speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant that is important in many areas of physics. The speed of light is exactly equal to ). According to the special theory of relativity, is the upper limit fo ...
, and with high-energy phenomena.
With Lorentz symmetry, additional structures come into play. They are defined by the set of light cones (see image). The light-cones define a causal structure: for each
event , there is a set of events that can, in principle, either influence or be influenced by via signals or interactions that do not need to travel faster than light (such as event in the image), and a set of events for which such an influence is impossible (such as event in the image). These sets are observer-independent. In conjunction with the world-lines of freely falling particles, the light-cones can be used to reconstruct the spacetime's semi-Riemannian metric, at least up to a positive scalar factor. In mathematical terms, this defines a
conformal structure or conformal geometry.
Special relativity is defined in the absence of gravity. For practical applications, it is a suitable model whenever gravity can be neglected. Bringing gravity into play, and assuming the universality of free fall motion, an analogous reasoning as in the previous section applies: there are no global
inertial frame
In classical physics and special relativity, an inertial frame of reference (also called inertial reference frame, inertial frame, inertial space, or Galilean reference frame) is a frame of reference that is not undergoing any acceleration. ...
s. Instead there are approximate inertial frames moving alongside freely falling particles. Translated into the language of spacetime: the straight
time-like lines that define a gravity-free inertial frame are deformed to lines that are curved relative to each other, suggesting that the inclusion of gravity necessitates a change in spacetime geometry.
A priori, it is not clear whether the new local frames in free fall coincide with the reference frames in which the laws of special relativity hold—that theory is based on the propagation of light, and thus on electromagnetism, which could have a different set of preferred frames. But using different assumptions about the special-relativistic frames (such as their being earth-fixed, or in free fall), one can derive different predictions for the gravitational redshift, that is, the way in which the frequency of light shifts as the light propagates through a gravitational field (cf.
below
Below may refer to:
*Earth
* Ground (disambiguation)
* Soil
* Floor
* Bottom (disambiguation)
* Less than
*Temperatures below freezing
* Hell or underworld
People with the surname
* Ernst von Below (1863–1955), German World War I general
* Fr ...
). The actual measurements show that free-falling frames are the ones in which light propagates as it does in special relativity. The generalization of this statement, namely that the laws of special relativity hold to good approximation in freely falling (and non-rotating) reference frames, is known as the
Einstein equivalence principle
In the theory of general relativity, the equivalence principle is the equivalence of Gravitational mass, gravitational and Mass#Inertial mass, inertial mass, and Albert Einstein's observation that the gravitational "force" as experienced local ...
, a crucial guiding principle for generalizing special-relativistic physics to include gravity.
The same experimental data shows that time as measured by clocks in a gravitational field—
proper time
In relativity, proper time (from Latin, meaning ''own time'') along a timelike world line is defined as the time as measured by a clock following that line. It is thus independent of coordinates, and is a Lorentz scalar. The proper time interval ...
, to give the technical term—does not follow the rules of special relativity. In the language of spacetime geometry, it is not measured by the
Minkowski metric
In mathematical physics, Minkowski space (or Minkowski spacetime) () is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inerti ...
. As in the Newtonian case, this is suggestive of a more general geometry. At small scales, all reference frames that are in free fall are equivalent, and approximately Minkowskian. Consequently, we are now dealing with a curved generalization of Minkowski space. The
metric tensor
In the mathematical field of differential geometry, a metric tensor (or simply metric) is an additional structure on a manifold (such as a surface) that allows defining distances and angles, just as the inner product on a Euclidean space allo ...
that defines the geometry—in particular, how lengths and angles are measured—is not the Minkowski metric of special relativity, it is a generalization known as a semi- or
pseudo-Riemannian metric. Furthermore, each Riemannian metric is naturally associated with one particular kind of connection, the
Levi-Civita connection
In Riemannian or pseudo Riemannian geometry (in particular the Lorentzian geometry of general relativity), the Levi-Civita connection is the unique affine connection on the tangent bundle of a manifold (i.e. affine connection) that preserves ...
, and this is, in fact, the connection that satisfies the equivalence principle and makes space locally Minkowskian (that is, in suitable
locally inertial coordinates, the metric is Minkowskian, and its first partial derivatives and the connection coefficients vanish).
Einstein's equations
Having formulated the relativistic, geometric version of the effects of gravity, the question of gravity's source remains. In Newtonian gravity, the source is mass. In special relativity, mass turns out to be part of a more general quantity called the
energy–momentum tensor Energy–momentum may refer to:
* Four-momentum
*Stress–energy tensor
*Energy–momentum relation
In physics, the energy–momentum relation, or relativistic dispersion relation, is the relativistic equation relating total energy (which is also ...
, which includes both
energy
In physics, energy (from Ancient Greek: ἐνέργεια, ''enérgeia'', “activity”) is the quantitative property that is transferred to a body or to a physical system, recognizable in the performance of work and in the form of hea ...
and momentum
densities as well as
stress:
pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country a ...
and shear. Using the equivalence principle, this tensor is readily generalized to curved spacetime. Drawing further upon the analogy with geometric Newtonian gravity, it is natural to assume that the
field equation for gravity relates this tensor and the
Ricci tensor
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, is a geometric object which is determined by a choice of Riemannian or pseudo-Riemannian metric on a manifold. It can be considered, broadly, as a measur ...
, which describes a particular class of tidal effects: the change in volume for a small cloud of test particles that are initially at rest, and then fall freely. In special relativity,
conservation of energy
In physics and chemistry, the law of conservation of energy states that the total energy of an isolated system remains constant; it is said to be ''conserved'' over time. This law, first proposed and tested by Émilie du Châtelet, means tha ...
–momentum corresponds to the statement that the energy–momentum tensor is
divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of t ...
-free. This formula, too, is readily generalized to curved spacetime by replacing partial derivatives with their curved-
manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a ...
counterparts,
covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differ ...
s studied in differential geometry. With this additional condition—the covariant divergence of the energy–momentum tensor, and hence of whatever is on the other side of the equation, is zero—the simplest set of equations are what are called Einstein's (field) equations:
On the left-hand side is the
Einstein tensor
In differential geometry, the Einstein tensor (named after Albert Einstein; also known as the trace-reversed Ricci tensor) is used to express the curvature of a pseudo-Riemannian manifold. In general relativity, it occurs in the Einstein field e ...
,
, which is symmetric and a specific divergence-free combination of the Ricci tensor
and the metric. In particular,
:
is the curvature scalar. The Ricci tensor itself is related to the more general
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor (after Bernhard Riemann and Elwin Bruno Christoffel) is the most common way used to express the curvature of Riemannian manifolds ...
as
:
On the right-hand side, ''
'' is the energy–momentum tensor. All tensors are written in
abstract index notation
Abstract index notation (also referred to as slot-naming index notation) is a mathematical notation for tensors and spinors that uses indices to indicate their types, rather than their components in a particular basis. The indices are mere placeh ...
. Matching the theory's prediction to observational results for
planet
A planet is a large, rounded astronomical body that is neither a star nor its remnant. The best available theory of planet formation is the nebular hypothesis, which posits that an interstellar cloud collapses out of a nebula to create a ...
ary
orbit
In celestial mechanics, an orbit is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such a ...
s or, equivalently, assuring that the weak-gravity, low-speed limit is Newtonian mechanics, the proportionality constant is found to be
, where
is the
gravitational constant and
the speed of light in vacuum. When there is no matter present, so that the energy–momentum tensor vanishes, the results are the vacuum Einstein equations,
:
In general relativity, the
world line
The world line (or worldline) of an object is the path that an object traces in 4- dimensional spacetime. It is an important concept in modern physics, and particularly theoretical physics.
The concept of a "world line" is distinguished from c ...
of a particle free from all external, non-gravitational force is a particular type of geodesic in curved spacetime. In other words, a freely moving or falling particle always moves along a geodesic.
The
geodesic equation is:
:
where
is a scalar parameter of motion (e.g. the
proper time
In relativity, proper time (from Latin, meaning ''own time'') along a timelike world line is defined as the time as measured by a clock following that line. It is thus independent of coordinates, and is a Lorentz scalar. The proper time interval ...
), and
are
Christoffel symbols
In mathematics and physics, the Christoffel symbols are an array of numbers describing a metric connection. The metric connection is a specialization of the affine connection to surfaces or other manifolds endowed with a metric, allowing dis ...
(sometimes called the
affine connection
In differential geometry, an affine connection is a geometric object on a smooth manifold which ''connects'' nearby tangent spaces, so it permits tangent vector fields to be differentiated as if they were functions on the manifold with values ...
coefficients or
Levi-Civita connection
In Riemannian or pseudo Riemannian geometry (in particular the Lorentzian geometry of general relativity), the Levi-Civita connection is the unique affine connection on the tangent bundle of a manifold (i.e. affine connection) that preserves ...
coefficients) which is symmetric in the two lower indices. Greek indices may take the values: 0, 1, 2, 3 and the
summation convention
In mathematics, especially the usage of linear algebra in Mathematical physics, Einstein notation (also known as the Einstein summation convention or Einstein summation notation) is a notational convention that implies summation over a set of ...
is used for repeated indices
and
. The quantity on the left-hand-side of this equation is the acceleration of a particle, and so this equation is analogous to
Newton's laws of motion
Newton's laws of motion are three basic laws of classical mechanics that describe the relationship between the motion of an object and the forces acting on it. These laws can be paraphrased as follows:
# A body remains at rest, or in moti ...
which likewise provide formulae for the acceleration of a particle. This equation of motion employs the
Einstein notation
In mathematics, especially the usage of linear algebra in Mathematical physics, Einstein notation (also known as the Einstein summation convention or Einstein summation notation) is a notational convention that implies summation over a set of ...
, meaning that repeated indices are summed (i.e. from zero to three). The Christoffel symbols are functions of the four spacetime coordinates, and so are independent of the velocity or acceleration or other characteristics of a
test particle In physical theories, a test particle, or test charge, is an idealized model of an object whose physical properties (usually mass, charge, or size) are assumed to be negligible except for the property being studied, which is considered to be insu ...
whose motion is described by the geodesic equation.
Total force in general relativity
In general relativity, the effective
gravitational potential energy
Gravitational energy or gravitational potential energy is the potential energy a massive object has in relation to another massive object due to gravity. It is the potential energy associated with the gravitational field, which is released (conv ...
of an object of mass ''m'' rotating around a massive central body ''M'' is given by
:
A conservative total
force
In physics, a force is an influence that can change the motion of an object. A force can cause an object with mass to change its velocity (e.g. moving from a state of rest), i.e., to accelerate. Force can also be described intuitively as a ...
can then be obtained as
:
where ''L'' is the
angular momentum
In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity—the total angular momentum of a closed sy ...
. The first term represents the
Newton's force of gravity, which is described by the inverse-square law. The second term represents the
centrifugal force
In Newtonian mechanics, the centrifugal force is an inertial force (also called a "fictitious" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It is directed away from an axis which is parallel ...
in the circular motion. The third term represents the relativistic effect.
Alternatives to general relativity
There are
alternatives to general relativity built upon the same premises, which include additional rules and/or constraints, leading to different field equations. Examples are
Whitehead's theory,
Brans–Dicke theory,
teleparallelism
Teleparallelism (also called teleparallel gravity), was an attempt by Albert Einstein to base a unified theory of electromagnetism and gravity on the mathematical structure of distant parallelism, also referred to as absolute or teleparallelism. ...
,
''f''(''R'') gravity and
Einstein–Cartan theory
In theoretical physics, the Einstein–Cartan theory, also known as the Einstein–Cartan–Sciama–Kibble theory, is a classical theory of gravitation similar to general relativity. The theory was first proposed by Élie Cartan in 1922. Einstein ...
.
Definition and basic applications
The derivation outlined in the previous section contains all the information needed to define general relativity, describe its key properties, and address a question of crucial importance in physics, namely how the theory can be used for model-building.
Definition and basic properties
General relativity is a
metric
Metric or metrical may refer to:
* Metric system, an internationally adopted decimal system of measurement
* An adjective indicating relation to measurement in general, or a noun describing a specific type of measurement
Mathematics
In mathem ...
theory of gravitation. At its core are
Einstein's equations
In the general theory of relativity, the Einstein field equations (EFE; also known as Einstein's equations) relate the geometry of spacetime to the distribution of matter within it.
The equations were published by Einstein in 1915 in the fo ...
, which describe the relation between the geometry of a four-dimensional
pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold, also called a semi-Riemannian manifold, is a differentiable manifold with a metric tensor that is everywhere nondegenerate. This is a generalization of a Riemannian manifold in which t ...
representing spacetime, and the
energy–momentum contained in that spacetime. Phenomena that in classical mechanics are ascribed to the action of the force of gravity (such as
free-fall
In Newtonian physics, free fall is any motion of a body where gravity is the only force acting upon it. In the context of general relativity, where gravitation is reduced to a space-time curvature, a body in free fall has no force acting on i ...
, orbital motion, and
spacecraft
A spacecraft is a vehicle or machine designed to spaceflight, fly in outer space. A type of artificial satellite, spacecraft are used for a variety of purposes, including Telecommunications, communications, Earth observation satellite, Earth ...
trajectories
A trajectory or flight path is the path that an object with mass in motion follows through space as a function of time. In classical mechanics, a trajectory is defined by Hamiltonian mechanics via canonical coordinates; hence, a complete traj ...
), correspond to inertial motion within a curved geometry of spacetime in general relativity; there is no gravitational force deflecting objects from their natural, straight paths. Instead, gravity corresponds to changes in the properties of space and time, which in turn changes the straightest-possible paths that objects will naturally follow. The curvature is, in turn, caused by the energy–momentum of matter. Paraphrasing the relativist
John Archibald Wheeler
John Archibald Wheeler (July 9, 1911April 13, 2008) was an American theoretical physicist. He was largely responsible for reviving interest in general relativity in the United States after World War II. Wheeler also worked with Niels Bohr in e ...
, spacetime tells matter how to move; matter tells spacetime how to curve.
While general relativity replaces the
scalar gravitational potential of classical physics by a symmetric
rank
Rank is the relative position, value, worth, complexity, power, importance, authority, level, etc. of a person or object within a ranking, such as:
Level or position in a hierarchical organization
* Academic rank
* Diplomatic rank
* Hierarchy
* H ...
-two
tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors may map between different objects such as vectors, scalars, and even other tens ...
, the latter reduces to the former in certain
limiting cases. For
weak gravitational fields and
slow speed relative to the speed of light, the theory's predictions converge on those of Newton's law of universal gravitation.
As it is constructed using tensors, general relativity exhibits
general covariance
In theoretical physics, general covariance, also known as diffeomorphism covariance or general invariance, consists of the invariance of the ''form'' of physical laws under arbitrary differentiable coordinate transformations. The essential idea i ...
: its laws—and further laws formulated within the general relativistic framework—take on the same form in all
coordinate systems. Furthermore, the theory does not contain any invariant geometric background structures, i.e. it is
background independent. It thus satisfies a more stringent
general principle of relativity, namely that the
laws of physics
Scientific laws or laws of science are statements, based on repeated experiments or observations, that describe or predict a range of natural phenomena. The term ''law'' has diverse usage in many cases (approximate, accurate, broad, or narrow) a ...
are the same for all observers.
Locally, as expressed in the equivalence principle, spacetime is
Minkowskian, and the laws of physics exhibit
local Lorentz invariance.
Model-building
The core concept of general-relativistic model-building is that of a
solution of Einstein's equations. Given both Einstein's equations and suitable equations for the properties of matter, such a solution consists of a specific semi-Riemannian manifold (usually defined by giving the metric in specific coordinates), and specific matter fields defined on that manifold. Matter and geometry must satisfy Einstein's equations, so in particular, the matter's energy–momentum tensor must be divergence-free. The matter must, of course, also satisfy whatever additional equations were imposed on its properties. In short, such a solution is a model universe that satisfies the laws of general relativity, and possibly additional laws governing whatever matter might be present.
Einstein's equations are nonlinear partial differential equations and, as such, difficult to solve exactly. Nevertheless, a number of
exact solutions
In mathematics, integrability is a property of certain dynamical systems. While there are several distinct formal definitions, informally speaking, an integrable system is a dynamical system with sufficiently many conserved quantities, or first i ...
are known, although only a few have direct physical applications. The best-known exact solutions, and also those most interesting from a physics point of view, are the
Schwarzschild solution
In Einstein's theory of general relativity, the Schwarzschild metric (also known as the Schwarzschild solution) is an
exact solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assumpt ...
, the
Reissner–Nordström solution and the
Kerr metric
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of ...
, each corresponding to a certain type of black hole in an otherwise empty universe, and the
Friedmann–Lemaître–Robertson–Walker and
de Sitter universe
A de Sitter universe is a cosmological solution to the Einstein field equations of general relativity, named after Willem de Sitter. It models the universe as spatially flat and neglects ordinary matter, so the dynamics of the universe are dominat ...
s, each describing an expanding cosmos. Exact solutions of great theoretical interest include the
Gödel universe (which opens up the intriguing possibility of
time travel
Time travel is the concept of movement between certain points in time, analogous to movement between different points in space by an object or a person, typically with the use of a hypothetical device known as a time machine. Time travel is a ...
in curved spacetimes), the
Taub–NUT solution (a model universe that is
homogeneous
Homogeneity and heterogeneity are concepts often used in the sciences and statistics relating to the uniformity of a substance or organism. A material or image that is homogeneous is uniform in composition or character (i.e. color, shape, siz ...
, but
anisotropic
Anisotropy () is the property of a material which allows it to change or assume different properties in different directions, as opposed to isotropy. It can be defined as a difference, when measured along different axes, in a material's phys ...
), and
anti-de Sitter space
In mathematics and physics, ''n''-dimensional anti-de Sitter space (AdS''n'') is a maximally symmetric Lorentzian manifold with constant negative scalar curvature. Anti-de Sitter space and de Sitter space are named after Willem de Sitter (18 ...
(which has recently come to prominence in the context of what is called the
Maldacena conjecture
Juan Martín Maldacena (born September 10, 1968) is an Argentine theoretical physicist and the Carl P. Feinberg Professor in the School of Natural Sciences at the Institute for Advanced Study, Princeton. He has made significant contributions to ...
).
Given the difficulty of finding exact solutions, Einstein's field equations are also solved frequently by
numerical integration
In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations ...
on a computer, or by considering small perturbations of exact solutions. In the field of
numerical relativity
Numerical relativity is one of the branches of general relativity that uses numerical methods and algorithms to solve and analyze problems. To this end, supercomputers are often employed to study black holes, gravitational waves, neutron stars and ...
, powerful computers are employed to simulate the geometry of spacetime and to solve Einstein's equations for interesting situations such as two colliding black holes. In principle, such methods may be applied to any system, given sufficient computer resources, and may address fundamental questions such as
naked singularities. Approximate solutions may also be found by
perturbation theories such as
linearized gravity
In the theory of general relativity, linearized gravity is the application of perturbation theory to the metric tensor that describes the geometry of spacetime. As a consequence, linearized gravity is an effective method for modeling the effect ...
and its generalization, the
post-Newtonian expansion
In general relativity, the post-Newtonian expansions (PN expansions) are used for finding an approximate solution of the Einstein field equations for the metric tensor. The approximations are expanded in small parameters which express orders of ...
, both of which were developed by Einstein. The latter provides a systematic approach to solving for the geometry of a spacetime that contains a distribution of matter that moves slowly compared with the speed of light. The expansion involves a series of terms; the first terms represent Newtonian gravity, whereas the later terms represent ever smaller corrections to Newton's theory due to general relativity. An extension of this expansion is the parametrized post-Newtonian (PPN) formalism, which allows quantitative comparisons between the predictions of general relativity and alternative theories.
Consequences of Einstein's theory
General relativity has a number of physical consequences. Some follow directly from the theory's axioms, whereas others have become clear only in the course of many years of research that followed Einstein's initial publication.
Gravitational time dilation and frequency shift

Assuming that the equivalence principle holds, gravity influences the passage of time. Light sent down into a
gravity well
The Hill sphere of an astronomical body is the region in which it dominates the attraction of satellites. To be retained by a planet, a moon must have an orbit that lies within the planet's Hill sphere. That moon would, in turn, have a Hill sp ...
is
blueshift
In physics, a redshift is an increase in the wavelength, and corresponding decrease in the frequency and photon energy, of electromagnetic radiation (such as light). The opposite change, a decrease in wavelength and simultaneous increase in fr ...
ed, whereas light sent in the opposite direction (i.e., climbing out of the gravity well) is
redshift
In physics, a redshift is an increase in the wavelength, and corresponding decrease in the frequency and photon energy, of electromagnetic radiation (such as light). The opposite change, a decrease in wavelength and simultaneous increase in f ...
ed; collectively, these two effects are known as the gravitational frequency shift. More generally, processes close to a massive body run more slowly when compared with processes taking place farther away; this effect is known as gravitational time dilation.
Gravitational redshift has been measured in the laboratory and using astronomical observations. Gravitational time dilation in the Earth's gravitational field has been measured numerous times using
atomic clocks
An atomic clock is a clock that measures time by monitoring the resonant frequency of atoms. It is based on atoms having different energy levels. Electron states in an atom are associated with different energy levels, and in transitions betwee ...
, while ongoing validation is provided as a side effect of the operation of the
Global Positioning System (GPS). Tests in stronger gravitational fields are provided by the observation of
binary pulsars. All results are in agreement with general relativity. However, at the current level of accuracy, these observations cannot distinguish between general relativity and other theories in which the equivalence principle is valid.
Light deflection and gravitational time delay

General relativity predicts that the path of light will follow the curvature of spacetime as it passes near a star. This effect was initially confirmed by observing the light of stars or distant quasars being deflected as it passes the
Sun
The Sun is the star at the center of the Solar System. It is a nearly perfect ball of hot plasma, heated to incandescence by nuclear fusion reactions in its core. The Sun radiates this energy mainly as light, ultraviolet, and infrared rad ...
.
This and related predictions follow from the fact that light follows what is called a light-like or
null geodesic—a generalization of the straight lines along which light travels in classical physics. Such geodesics are the generalization of the
invariance
Invariant and invariance may refer to:
Computer science
* Invariant (computer science), an expression whose value doesn't change during program execution
** Loop invariant, a property of a program loop that is true before (and after) each iterat ...
of lightspeed in special relativity. As one examines suitable model spacetimes (either the exterior Schwarzschild solution or, for more than a single mass, the post-Newtonian expansion), several effects of gravity on light propagation emerge. Although the bending of light can also be derived by extending the universality of free fall to light, the angle of deflection resulting from such calculations is only half the value given by general relativity.
Closely related to light deflection is the gravitational time delay (or Shapiro delay), the phenomenon that light signals take longer to move through a gravitational field than they would in the absence of that field. There have been numerous successful tests of this prediction. In the
parameterized post-Newtonian formalism (PPN), measurements of both the deflection of light and the gravitational time delay determine a parameter called γ, which encodes the influence of gravity on the geometry of space.
Gravitational waves

Predicted in 1916 by Albert Einstein, there are gravitational waves: ripples in the metric of spacetime that propagate at the speed of light. These are one of several analogies between weak-field gravity and electromagnetism in that, they are analogous to
electromagnetic wave
In physics, electromagnetic radiation (EMR) consists of waves of the electromagnetic (EM) field, which propagate through space and carry momentum and electromagnetic radiant energy. It includes radio waves, microwaves, infrared, (visible ...
s. On 11 February 2016, the Advanced LIGO team announced that they had
directly detected gravitational waves from a
pair
Pair or PAIR or Pairing may refer to:
Government and politics
* Pair (parliamentary convention), matching of members unable to attend, so as not to change the voting margin
* ''Pair'', a member of the Prussian House of Lords
* ''Pair'', the Frenc ...
of black holes
merging
Merge, merging, or merger may refer to:
Concepts
* Merge (traffic), the reduction of the number of lanes on a road
* Merge (linguistics), a basic syntactic operation in generative syntax in the Minimalist Program
* Merger (politics), the co ...
.
The simplest type of such a wave can be visualized by its action on a ring of freely floating particles. A sine wave propagating through such a ring towards the reader distorts the ring in a characteristic, rhythmic fashion (animated image to the right). Since Einstein's equations are
non-linear
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other ...
, arbitrarily strong gravitational waves do not obey
linear superposition
The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So tha ...
, making their description difficult. However, linear approximations of gravitational waves are sufficiently accurate to describe the exceedingly weak waves that are expected to arrive here on Earth from far-off cosmic events, which typically result in relative distances increasing and decreasing by
or less. Data analysis methods routinely make use of the fact that these linearized waves can be
Fourier decomposed.
Some exact solutions describe gravitational waves without any approximation, e.g., a wave train traveling through empty space or
Gowdy universes, varieties of an expanding cosmos filled with gravitational waves. But for gravitational waves produced in astrophysically relevant situations, such as the merger of two black holes, numerical methods are presently the only way to construct appropriate models.
Orbital effects and the relativity of direction
General relativity differs from classical mechanics in a number of predictions concerning orbiting bodies. It predicts an overall rotation (
precession
Precession is a change in the orientation of the rotational axis of a rotating body. In an appropriate reference frame it can be defined as a change in the first Euler angle, whereas the third Euler angle defines the rotation itself. In o ...
) of planetary orbits, as well as orbital decay caused by the emission of gravitational waves and effects related to the relativity of direction.
Precession of apsides

In general relativity, the
apsides
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary body. For example, the apsides of the Earth are called the aphelion and perihelion.
General description
There are two apsides in any ell ...
of any orbit (the point of the orbiting body's closest approach to the system's
center of mass) will
precess; the orbit is not an
ellipse, but akin to an ellipse that rotates on its focus, resulting in a
rose curve-like shape (see image). Einstein first derived this result by using an approximate metric representing the Newtonian limit and treating the orbiting body as a
test particle In physical theories, a test particle, or test charge, is an idealized model of an object whose physical properties (usually mass, charge, or size) are assumed to be negligible except for the property being studied, which is considered to be insu ...
. For him, the fact that his theory gave a straightforward explanation of Mercury's anomalous perihelion shift, discovered earlier by
Urbain Le Verrier
Urbain Jean Joseph Le Verrier FRS (FOR) HFRSE (; 11 March 1811 – 23 September 1877) was a French astronomer and mathematician who specialized in celestial mechanics and is best known for predicting the existence and position of Neptune using ...
in 1859, was important evidence that he had at last identified the correct form of the gravitational field equations.
The effect can also be derived by using either the exact Schwarzschild metric (describing spacetime around a spherical mass) or the much more general
post-Newtonian formalism. It is due to the influence of gravity on the geometry of space and to the contribution of
self-energy
In quantum field theory, the energy that a particle has as a result of changes that it causes in its environment defines self-energy \Sigma, and represents the contribution to the particle's energy, or effective mass, due to interactions between ...
to a body's gravity (encoded in the
nonlinearity
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other ...
of Einstein's equations). Relativistic precession has been observed for all planets that allow for accurate precession measurements (Mercury, Venus, and Earth), as well as in binary pulsar systems, where it is larger by five
orders of magnitude
An order of magnitude is an approximation of the logarithm of a value relative to some contextually understood reference value, usually 10, interpreted as the base of the logarithm and the representative of values of magnitude one. Logarithmic di ...
.
In general relativity the perihelion shift
, expressed in radians per revolution, is approximately given by
:
where:
*
is the
semi-major axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the lo ...
*
is the
orbital period
The orbital period (also revolution period) is the amount of time a given astronomical object takes to complete one orbit around another object. In astronomy, it usually applies to planets or asteroids orbiting the Sun, moons orbiting planets ...
*
is the speed of light in vacuum
*
is the
orbital eccentricity
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values b ...
Orbital decay

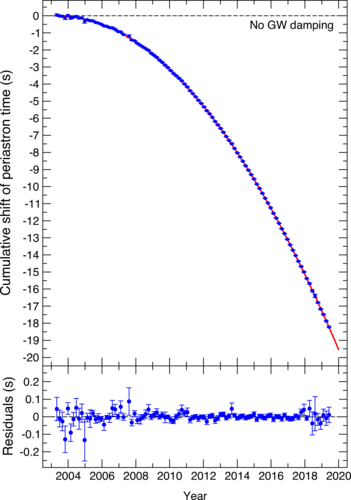
According to general relativity, a
binary system will emit gravitational waves, thereby losing energy. Due to this loss, the distance between the two orbiting bodies decreases, and so does their orbital period. Within the
Solar System
The Solar System Capitalization of the name varies. The International Astronomical Union, the authoritative body regarding astronomical nomenclature, specifies capitalizing the names of all individual astronomical objects but uses mixed "Solar ...
or for ordinary
double star
In observational astronomy, a double star or visual double is a pair of stars that appear close to each other as viewed from Earth, especially with the aid of optical telescopes.
This occurs because the pair either forms a binary star (i.e. a ...
s, the effect is too small to be observable. This is not the case for a close binary pulsar, a system of two orbiting
neutron star
A neutron star is the collapsed core of a massive supergiant star, which had a total mass of between 10 and 25 solar masses, possibly more if the star was especially metal-rich. Except for black holes and some hypothetical objects (e.g. w ...
s, one of which is a
pulsar
A pulsar (from ''pulsating radio source'') is a highly magnetized rotating neutron star that emits beams of electromagnetic radiation out of its magnetic poles. This radiation can be observed only when a beam of emission is pointing toward E ...
: from the pulsar, observers on Earth receive a regular series of radio pulses that can serve as a highly accurate clock, which allows precise measurements of the orbital period. Because neutron stars are immensely compact, significant amounts of energy are emitted in the form of gravitational radiation.
The first observation of a decrease in orbital period due to the emission of gravitational waves was made by
Hulse and
Taylor
Taylor, Taylors or Taylor's may refer to:
People
* Taylor (surname)
** List of people with surname Taylor
* Taylor (given name), including Tayla and Taylah
* Taylor sept, a branch of Scottish clan Cameron
* Justice Taylor (disambiguation)
...
, using the binary pulsar
PSR1913+16 they had discovered in 1974. This was the first detection of gravitational waves, albeit indirect, for which they were awarded the 1993
Nobel Prize
The Nobel Prizes ( ; sv, Nobelpriset ; no, Nobelprisen ) are five separate prizes that, according to Alfred Nobel's will of 1895, are awarded to "those who, during the preceding year, have conferred the greatest benefit to humankind." Alfre ...
in physics. Since then, several other binary pulsars have been found, in particular the double pulsar
PSR J0737−3039, where both stars are pulsars and which was last reported to also be in agreement with general relativity in 2021 after 16 years of observations.
Geodetic precession and frame-dragging
Several relativistic effects are directly related to the relativity of direction. One is
geodetic precession: the axis direction of a
gyroscope in free fall in curved spacetime will change when compared, for instance, with the direction of light received from distant stars—even though such a gyroscope represents the way of keeping a direction as stable as possible ("
parallel transport
In geometry, parallel transport (or parallel translation) is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection (a covariant derivative or connection on the tangent b ...
"). For the Moon–Earth system, this effect has been measured with the help of
lunar laser ranging. More recently, it has been measured for test masses aboard the satellite
Gravity Probe B to a precision of better than 0.3%.
Near a rotating mass, there are gravitomagnetic or
frame-dragging
Frame-dragging is an effect on spacetime, predicted by Albert Einstein's general theory of relativity, that is due to non-static stationary distributions of mass–energy. A stationary field is one that is in a steady state, but the masses c ...
effects. A distant observer will determine that objects close to the mass get "dragged around". This is most extreme for
rotating black holes where, for any object entering a zone known as the
ergosphere, rotation is inevitable. Such effects can again be tested through their influence on the orientation of gyroscopes in free fall. Somewhat controversial tests have been performed using the
LAGEOS
LAGEOS, Laser Geodynamics Satellite or Laser Geometric Environmental Observation Survey, are a series of two scientific research satellites designed to provide an orbiting laser ranging benchmark for geodynamical studies of the Earth. Each satel ...
satellites, confirming the relativistic prediction. Also the
Mars Global Surveyor
''Mars Global Surveyor'' (MGS) was an American robotic space probe developed by NASA's Jet Propulsion Laboratory and launched November 1996. MGS was a global mapping mission that examined the entire planet, from the ionosphere down through t ...
probe around Mars has been used.
Interpretations
Neo-Lorentzian Interpretation
Examples of prominent physicists who support neo-Lorentzian explanations of general relativity are
Franco Selleri
Franco Selleri (Bologna, Italy, 9 October 1936 – 20 November 2013) was an Italian theoretical physicist and professor at the Università degli Studi di Bari Aldo Moro. He received his Doctorate / Ph.D. cum laude at the Università di Bologna i ...
and
Antony Valentini.
Astrophysical applications
Gravitational lensing

The deflection of light by gravity is responsible for a new class of astronomical phenomena. If a massive object is situated between the astronomer and a distant target object with appropriate mass and relative distances, the astronomer will see multiple distorted images of the target. Such effects are known as gravitational lensing. Depending on the configuration, scale, and mass distribution, there can be two or more images, a bright ring known as an
Einstein ring
An Einstein ring, also known as an Einstein–Chwolson ring or Chwolson ring (named for Orest Chwolson), is created when light from a galaxy or star passes by a massive object en route to the Earth. Due to gravitational lensing, the light is dive ...
, or partial rings called arcs.
The
earliest example was discovered in 1979; since then, more than a hundred gravitational lenses have been observed. Even if the multiple images are too close to each other to be resolved, the effect can still be measured, e.g., as an overall brightening of the target object; a number of such "
microlensing
Gravitational microlensing is an astronomical phenomenon due to the gravitational lens effect. It can be used to detect objects that range from the mass of a planet to the mass of a star, regardless of the light they emit. Typically, astronomers ...
events" have been observed.
Gravitational lensing has developed into a tool of
observational astronomy
Observational astronomy is a division of astronomy that is concerned with recording data about the observable universe, in contrast with theoretical astronomy, which is mainly concerned with calculating the measurable implications of physical ...
. It is used to detect the presence and distribution of
dark matter
Dark matter is a hypothetical form of matter thought to account for approximately 85% of the matter in the universe. Dark matter is called "dark" because it does not appear to interact with the electromagnetic field, which means it does not ab ...
, provide a "natural telescope" for observing distant galaxies, and to obtain an independent estimate of the
Hubble constant
Hubble's law, also known as the Hubble–Lemaître law, is the observation in physical cosmology that galaxies are moving away from Earth at speeds proportional to their distance. In other words, the farther they are, the faster they are moving ...
. Statistical evaluations of lensing data provide valuable insight into the structural evolution of
galaxies
A galaxy is a system of stars, stellar remnants, interstellar gas, dust, dark matter, bound together by gravity. The word is derived from the Greek ' (), literally 'milky', a reference to the Milky Way galaxy that contains the Solar System. ...
.
Gravitational-wave astronomy

Observations of binary pulsars provide strong indirect evidence for the existence of gravitational waves (see
Orbital decay
Orbital decay is a gradual decrease of the distance between two orbiting bodies at their closest approach (the periapsis) over many orbital periods. These orbiting bodies can be a planet and its satellite, a star and any object orbiting it, or ...
, above). Detection of these waves is a major goal of current relativity-related research. Several land-based
gravitational wave detector
A gravitational-wave detector (used in a gravitational-wave observatory) is any device designed to measure tiny distortions of spacetime called gravitational waves. Since the 1960s, various kinds of gravitational-wave detectors have been buil ...
s are currently in operation, most notably the
interferometric detectors GEO 600,
LIGO
The Laser Interferometer Gravitational-Wave Observatory (LIGO) is a large-scale physics experiment and observatory designed to detect cosmic gravitational waves and to develop gravitational-wave observations as an astronomical tool. Two large o ...
(two detectors),
TAMA 300 and
VIRGO
Virgo may refer to:
* Virgo (astrology), the sixth astrological sign of the zodiac
* Virgo (constellation), a constellation
* Virgo Cluster, a cluster of galaxies in the constellation Virgo
* Virgo Stellar Stream, remains of a dwarf galaxy
*Virgo ...
. Various
pulsar timing arrays are using
millisecond pulsar
A millisecond pulsar (MSP) is a pulsar with a rotational period less than about 10 milliseconds. Millisecond pulsars have been detected in radio, X-ray, and gamma ray portions of the electromagnetic spectrum. The leading theory for the origin of ...
s to detect gravitational waves in the 10
−9 to 10
−6 hertz
The hertz (symbol: Hz) is the unit of frequency in the International System of Units (SI), equivalent to one event (or cycle) per second. The hertz is an SI derived unit whose expression in terms of SI base units is s−1, meaning that one her ...
frequency range, which originate from binary supermassive blackholes. A European space-based detector,
eLISA / NGO, is currently under development, with a precursor mission (
LISA Pathfinder) having launched in December 2015.
Observations of gravitational waves promise to complement observations in the
electromagnetic spectrum
The electromagnetic spectrum is the range of frequencies (the spectrum) of electromagnetic radiation and their respective wavelengths and photon energies.
The electromagnetic spectrum covers electromagnetic waves with frequencies ranging from ...
. They are expected to yield information about black holes and other dense objects such as neutron stars and white dwarfs, about certain kinds of
supernova implosions, and about processes in the very early universe, including the signature of certain types of hypothetical
cosmic string
Cosmic strings are hypothetical 1-dimensional topological defects which may have formed during a symmetry-breaking phase transition in the early universe when the topology of the vacuum manifold associated to this symmetry breaking was not simp ...
. In February 2016, the Advanced LIGO team announced that they had detected gravitational waves from a black hole merger.
Black holes and other compact objects

Whenever the ratio of an object's mass to its radius becomes sufficiently large, general relativity predicts the formation of a black hole, a region of space from which nothing, not even light, can escape. In the currently accepted models of
stellar evolution
Stellar evolution is the process by which a star changes over the course of time. Depending on the mass of the star, its lifetime can range from a few million years for the most massive to trillions of years for the least massive, which is con ...
, neutron stars of around 1.4
solar mass
The solar mass () is a standard unit of mass in astronomy, equal to approximately . It is often used to indicate the masses of other stars, as well as stellar clusters, nebulae, galaxies and black holes. It is approximately equal to the mass o ...
es, and stellar black holes with a few to a few dozen solar masses, are thought to be the final state for the evolution of massive stars. Usually a galaxy has one supermassive black hole with a few million to a few
billion
Billion is a word for a large number, and it has two distinct definitions:
*1,000,000,000, i.e. one thousand million, or (ten to the ninth power), as defined on the short scale. This is its only current meaning in English.
* 1,000,000,000,000, ...
solar masses in its center, and its presence is thought to have played an important role in the formation of the galaxy and larger cosmic structures.
Astronomically, the most important property of compact objects is that they provide a supremely efficient mechanism for converting gravitational energy into electromagnetic radiation.
Accretion, the falling of dust or gaseous matter onto stellar or supermassive black holes, is thought to be responsible for some spectacularly luminous astronomical objects, notably diverse kinds of active galactic nuclei on galactic scales and stellar-size objects such as microquasars. In particular, accretion can lead to
relativistic jet
An astrophysical jet is an astronomical phenomenon where outflows of ionised matter are emitted as an extended beam along the axis of rotation. When this greatly accelerated matter in the beam approaches the speed of light, astrophysical jets bec ...
s, focused beams of highly energetic particles that are being flung into space at almost light speed.
General relativity plays a central role in modelling all these phenomena, and observations provide strong evidence for the existence of black holes with the properties predicted by the theory.
Black holes are also sought-after targets in the search for gravitational waves (cf.
Gravitational waves
Gravitational waves are waves of the intensity of gravity generated by the accelerated masses of an orbital binary system that propagate as waves outward from their source at the speed of light. They were first proposed by Oliver Heaviside in 1 ...
, above). Merging
black hole binaries should lead to some of the strongest gravitational wave signals reaching detectors here on Earth, and the phase directly before the merger ("chirp") could be used as a "
standard candle
The cosmic distance ladder (also known as the extragalactic distance scale) is the succession of methods by which astronomers determine the distances to celestial objects. A ''direct'' distance measurement of an astronomical object is possible o ...
" to deduce the distance to the merger events–and hence serve as a probe of cosmic expansion at large distances. The gravitational waves produced as a stellar black hole plunges into a supermassive one should provide direct information about the supermassive black hole's geometry.
Cosmology

The current models of cosmology are based on
Einstein's field equations, which include the cosmological constant
since it has important influence on the large-scale dynamics of the cosmos,
:
where ''
'' is the spacetime metric.
Isotropic and homogeneous solutions of these enhanced equations, the
Friedmann–Lemaître–Robertson–Walker solutions, allow physicists to model a universe that has evolved over the past 14
billion
Billion is a word for a large number, and it has two distinct definitions:
*1,000,000,000, i.e. one thousand million, or (ten to the ninth power), as defined on the short scale. This is its only current meaning in English.
* 1,000,000,000,000, ...
years from a hot, early Big Bang phase. Once a small number of parameters (for example the universe's mean matter density) have been fixed by astronomical observation, further observational data can be used to put the models to the test. Predictions, all successful, include the initial abundance of chemical elements formed in a period of
primordial nucleosynthesis
In physical cosmology, Big Bang nucleosynthesis (abbreviated BBN, also known as primordial nucleosynthesis) is the production of nuclei other than those of the lightest isotope of hydrogen (hydrogen-1, 1H, having a single proton as a nucleus) d ...
, the large-scale structure of the universe, and the existence and properties of a "
thermal
A thermal column (or thermal) is a rising mass of buoyant air, a convective current in the atmosphere, that transfers heat energy vertically. Thermals are created by the uneven heating of Earth's surface from solar radiation, and are an example ...
echo" from the early cosmos, the
cosmic background radiation
Cosmic background radiation is electromagnetic radiation from the Big Bang. The origin of this radiation depends on the region of the spectrum that is observed. One component is the cosmic microwave background. This component is redshifted ph ...
.
Astronomical observations of the cosmological expansion rate allow the total amount of matter in the universe to be estimated, although the nature of that matter remains mysterious in part. About 90% of all matter appears to be dark matter, which has mass (or, equivalently, gravitational influence), but does not interact electromagnetically and, hence, cannot be observed directly. There is no generally accepted description of this new kind of matter, within the framework of known
particle physics
Particle physics or high energy physics is the study of fundamental particles and forces that constitute matter and radiation. The fundamental particles in the universe are classified in the Standard Model as fermions (matter particles) and ...
or otherwise. Observational evidence from redshift surveys of distant supernovae and measurements of the cosmic background radiation also show that the evolution of our universe is significantly influenced by a cosmological constant resulting in an acceleration of cosmic expansion or, equivalently, by a form of energy with an unusual
equation of state
In physics, chemistry, and thermodynamics, an equation of state is a thermodynamic equation relating state variables, which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature, or intern ...
, known as
dark energy
In physical cosmology and astronomy, dark energy is an unknown form of energy that affects the universe on the largest scales. The first observational evidence for its existence came from measurements of supernovas, which showed that the unive ...
, the nature of which remains unclear.
An
inflationary phase, an additional phase of strongly accelerated expansion at cosmic times of around 10
−33 seconds, was hypothesized in 1980 to account for several puzzling observations that were unexplained by classical cosmological models, such as the nearly perfect homogeneity of the cosmic background radiation. Recent measurements of the cosmic background radiation have resulted in the first evidence for this scenario. However, there is a bewildering variety of possible inflationary scenarios, which cannot be restricted by current observations. An even larger question is the physics of the earliest universe, prior to the inflationary phase and close to where the classical models predict the big bang
singularity. An authoritative answer would require a complete theory of quantum gravity, which has not yet been developed (cf. the section on
quantum gravity
Quantum gravity (QG) is a field of theoretical physics that seeks to describe gravity according to the principles of quantum mechanics; it deals with environments in which neither gravitational nor quantum effects can be ignored, such as in the v ...
, below).
Exotic solutions: time travel, warp drives
Kurt Gödel
Kurt Friedrich Gödel ( , ; April 28, 1906 – January 14, 1978) was a logician, mathematician, and philosopher. Considered along with Aristotle and Gottlob Frege to be one of the most significant logicians in history, Gödel had an imm ...
showed that solutions to Einstein's equations exist that contain
closed timelike curve
In mathematical physics, a closed timelike curve (CTC) is a world line in a Lorentzian manifold, of a material particle in spacetime, that is "closed", returning to its starting point. This possibility was first discovered by Willem Jacob van St ...
s (CTCs), which allow for loops in time. The solutions require extreme physical conditions unlikely ever to occur in practice, and it remains an open question whether further laws of physics will eliminate them completely. Since then, other—similarly impractical—GR solutions containing CTCs have been found, such as the
Tipler cylinder and
traversable wormholes.
Stephen Hawking introduced
chronology protection conjecture
The chronology protection conjecture is a hypothesis first proposed by Stephen Hawking that laws of physics beyond those of standard general relativity prevent time travel on all but microscopic scales - even when the latter theory states that it ...
, which is an assumption beyond those of standard general relativity to prevent
time travel
Time travel is the concept of movement between certain points in time, analogous to movement between different points in space by an object or a person, typically with the use of a hypothetical device known as a time machine. Time travel is a ...
.
Some
exact solutions in general relativity
In general relativity, an exact solution is a solution of the Einstein field equations whose derivation does not invoke simplifying assumptions, though the starting point for that derivation may be an idealized case like a perfectly spherical sh ...
such as
Alcubierre drive
The Alcubierre drive () is a speculative warp drive idea according to which a spacecraft could achieve apparent faster-than-light travel by contracting space in front of it and expanding space behind it, under the assumption that a configurable ...
present examples of
warp drive
A warp drive or a drive enabling space warp is a fictional superluminal spacecraft propulsion system in many science fiction works, most notably ''Star Trek'', and a subject of ongoing physics research. The general concept of "warp drive" was i ...
but these solutions requires exotic matter distribution, and generally suffers from semiclassical instability.
Advanced concepts
Asymptotic symmetries
The spacetime symmetry group for
special relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory regarding the relationship between space and time. In Albert Einstein's original treatment, the theory is based on two postulates:
# The law ...
is the
Poincaré group
The Poincaré group, named after Henri Poincaré (1906), was first defined by Hermann Minkowski (1908) as the group of Minkowski spacetime isometries. It is a ten-dimensional non-abelian Lie group that is of importance as a model in our und ...
, which is a ten-dimensional group of three Lorentz boosts, three rotations, and four spacetime translations. It is logical to ask what symmetries if any might apply in General Relativity. A tractable case might be to consider the symmetries of spacetime as seen by observers located far away from all sources of the gravitational field. The naive expectation for asymptotically flat spacetime symmetries might be simply to extend and reproduce the symmetries of flat spacetime of special relativity, ''viz.'', the Poincaré group.
In 1962
Hermann Bondi
Sir Hermann Bondi (1 November 1919 – 10 September 2005) was an Austrian- British mathematician and cosmologist.
He is best known for developing the steady state model of the universe with Fred Hoyle and Thomas Gold as an alternative to th ...
, M. G. van der Burg, A. W. Metzner
and
Rainer K. Sachs addressed this
asymptotic symmetry problem in order to investigate the flow of energy at infinity due to propagating
gravitational wave
Gravitational waves are waves of the intensity of gravity generated by the accelerated masses of an orbital binary system that propagate as waves outward from their source at the speed of light. They were first proposed by Oliver Heaviside in ...
s. Their first step was to decide on some physically sensible boundary conditions to place on the gravitational field at light-like infinity to characterize what it means to say a metric is asymptotically flat, making no ''a priori'' assumptions about the nature of the asymptotic symmetry group—not even the assumption that such a group exists. Then after designing what they considered to be the most sensible boundary conditions, they investigated the nature of the resulting asymptotic symmetry transformations that leave invariant the form of the boundary conditions appropriate for asymptotically flat gravitational fields. What they found was that the asymptotic symmetry transformations actually do form a group and the structure of this group does not depend on the particular gravitational field that happens to be present. This means that, as expected, one can separate the kinematics of spacetime from the dynamics of the gravitational field at least at spatial infinity. The puzzling surprise in 1962 was their discovery of a rich infinite-dimensional group (the so-called BMS group) as the asymptotic symmetry group, instead of the finite-dimensional Poincaré group, which is a subgroup of the BMS group. Not only are the Lorentz transformations asymptotic symmetry transformations, there are also additional transformations that are not Lorentz transformations but are asymptotic symmetry transformations. In fact, they found an additional infinity of transformation generators known as ''supertranslations''. This implies the conclusion that General Relativity (GR) does ''not'' reduce to special relativity in the case of weak fields at long distances. It turns out that the BMS symmetry, suitably modified, could be seen as a restatement of the universal soft graviton theorem in
quantum field theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines classical field theory, special relativity, and quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles a ...
(QFT), which relates universal infrared (soft) QFT with GR asymptotic spacetime symmetries.
Causal structure and global geometry

In general relativity, no material body can catch up with or overtake a light pulse. No influence from an event ''A'' can reach any other location ''X'' before light sent out at ''A'' to ''X''. In consequence, an exploration of all light worldlines (
null geodesics) yields key information about the spacetime's causal structure. This structure can be displayed using
Penrose–Carter diagrams in which infinitely large regions of space and infinite time intervals are shrunk ("
compactified") so as to fit onto a finite map, while light still travels along diagonals as in standard
spacetime diagram
A spacetime diagram is a graphical illustration of the properties of space and time in the special theory of relativity. Spacetime diagrams allow a qualitative understanding of the corresponding phenomena like time dilation and length contract ...
s.
Aware of the importance of causal structure,
Roger Penrose
Sir Roger Penrose (born 8 August 1931) is an English mathematician, mathematical physicist, philosopher of science and Nobel Laureate in Physics. He is Emeritus Rouse Ball Professor of Mathematics in the University of Oxford, an emeritus f ...
and others developed what is known as
global geometry
Spacetime topology is the topological structure of spacetime, a topic studied primarily in general relativity. This physical theory models gravitation as the curvature of a four dimensional Lorentzian manifold (a spacetime) and the concepts of t ...
. In global geometry, the object of study is not one particular solution (or family of solutions) to Einstein's equations. Rather, relations that hold true for all geodesics, such as the
Raychaudhuri equation, and additional non-specific assumptions about the nature of matter (usually in the form of
energy conditions
In relativistic classical field theories of gravitation, particularly general relativity, an energy condition is a generalization of the statement "the energy density of a region of space cannot be negative" in a relativistically-phrased mathe ...
) are used to derive general results.
Horizons
Using global geometry, some spacetimes can be shown to contain boundaries called
horizons, which demarcate one region from the rest of spacetime. The best-known examples are black holes: if mass is compressed into a sufficiently compact region of space (as specified in the
hoop conjecture, the relevant length scale is the
Schwarzschild radius
The Schwarzschild radius or the gravitational radius is a physical parameter in the Schwarzschild solution to Einstein's field equations that corresponds to the radius defining the event horizon of a Schwarzschild black hole. It is a characteris ...
), no light from inside can escape to the outside. Since no object can overtake a light pulse, all interior matter is imprisoned as well. Passage from the exterior to the interior is still possible, showing that the boundary, the black hole's ''horizon'', is not a physical barrier.

Early studies of black holes relied on explicit solutions of Einstein's equations, notably the spherically symmetric Schwarzschild solution (used to describe a
static black hole) and the axisymmetric
Kerr solution (used to describe a rotating,
stationary black hole, and introducing interesting features such as the ergosphere). Using global geometry, later studies have revealed more general properties of black holes. With time they become rather simple objects characterized by eleven parameters specifying: electric charge, mass–energy,
linear momentum
In Newtonian mechanics, momentum (more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass an ...
,
angular momentum
In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity—the total angular momentum of a closed sy ...
, and location at a specified time. This is stated by the
black hole uniqueness theorem
The no-hair theorem states that all stationary black hole solutions of the Einstein–Maxwell equations of gravitation and electromagnetism in general relativity can be completely characterized by only three independent ''externally'' observabl ...
: "black holes have no hair", that is, no distinguishing marks like the hairstyles of humans. Irrespective of the complexity of a gravitating object collapsing to form a black hole, the object that results (having emitted gravitational waves) is very simple.
Even more remarkably, there is a general set of laws known as
black hole mechanics, which is analogous to the
laws of thermodynamics
The laws of thermodynamics are a set of scientific laws which define a group of physical quantities, such as temperature, energy, and entropy, that characterize thermodynamic systems in thermodynamic equilibrium. The laws also use various pa ...
. For instance, by the second law of black hole mechanics, the area of the event horizon of a general black hole will never decrease with time, analogous to the
entropy
Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodyna ...
of a thermodynamic system. This limits the energy that can be extracted by classical means from a rotating black hole (e.g. by the
Penrose process
The Penrose process (also called Penrose mechanism) is theorised by Sir Roger Penrose as a means whereby energy can be extracted from a rotating black hole. The process takes advantage of the ergosphere --- a region of spacetime around the black ...
). There is strong evidence that the laws of black hole mechanics are, in fact, a subset of the laws of thermodynamics, and that the black hole area is proportional to its entropy. This leads to a modification of the original laws of black hole mechanics: for instance, as the second law of black hole mechanics becomes part of the second law of thermodynamics, it is possible for black hole area to decrease—as long as other processes ensure that, overall, entropy increases. As thermodynamical objects with non-zero temperature, black holes should emit
thermal radiation
Thermal radiation is electromagnetic radiation generated by the thermal motion of particles in matter. Thermal radiation is generated when heat from the movement of charges in the material (electrons and protons in common forms of matter) is ...
. Semi-classical calculations indicate that indeed they do, with the surface gravity playing the role of temperature in
Planck's law
In physics, Planck's law describes the spectral density of electromagnetic radiation emitted by a black body in thermal equilibrium at a given temperature , when there is no net flow of matter or energy between the body and its environment.
A ...
. This radiation is known as
Hawking radiation
Hawking radiation is theoretical black body radiation that is theorized to be released outside a black hole's event horizon because of relativistic quantum effects. It is named after the physicist Stephen Hawking, who developed a theoretical ar ...
(cf. the
quantum theory section, below).
There are other types of horizons. In an expanding universe, an observer may find that some regions of the past cannot be observed ("
particle horizon The particle horizon (also called the cosmological horizon, the comoving horizon (in Dodelson's text), or the cosmic light horizon) is the maximum distance from which light from particles could have traveled to the observer in the age of the univers ...
"), and some regions of the future cannot be influenced (event horizon). Even in flat Minkowski space, when described by an accelerated observer (
Rindler space), there will be horizons associated with a semi-classical radiation known as
Unruh radiation
The Unruh effect (also known as the Fulling–Davies–Unruh effect) is a kinematic prediction of quantum field theory that an accelerating observer will observe a thermal bath, like blackbody radiation, whereas an inertial observer would observe ...
.
Singularities
Another general feature of general relativity is the appearance of spacetime boundaries known as singularities. Spacetime can be explored by following up on timelike and lightlike geodesics—all possible ways that light and particles in free fall can travel. But some solutions of Einstein's equations have "ragged edges"—regions known as
spacetime singularities, where the paths of light and falling particles come to an abrupt end, and geometry becomes ill-defined. In the more interesting cases, these are "curvature singularities", where geometrical quantities characterizing spacetime curvature, such as the
Ricci scalar, take on infinite values. Well-known examples of spacetimes with future singularities—where worldlines end—are the Schwarzschild solution, which describes a singularity inside an eternal static black hole, or the Kerr solution with its ring-shaped singularity inside an eternal rotating black hole. The Friedmann–Lemaître–Robertson–Walker solutions and other spacetimes describing universes have past singularities on which worldlines begin, namely Big Bang singularities, and some have future singularities (
Big Crunch
The Big Crunch is a hypothetical scenario for the ultimate fate of the universe, in which the expansion of the universe eventually reverses and the universe recollapses, ultimately causing the cosmic scale factor to reach zero, an event potent ...
) as well.
Given that these examples are all highly symmetric—and thus simplified—it is tempting to conclude that the occurrence of singularities is an artifact of idealization. The famous
singularity theorems
Singularity or singular point may refer to:
Science, technology, and mathematics Mathematics
* Mathematical singularity, a point at which a given mathematical object is not defined or not "well-behaved", for example infinite or not differentiab ...
, proved using the methods of global geometry, say otherwise: singularities are a generic feature of general relativity, and unavoidable once the collapse of an object with realistic matter properties has proceeded beyond a certain stage and also at the beginning of a wide class of expanding universes. However, the theorems say little about the properties of singularities, and much of current research is devoted to characterizing these entities' generic structure (hypothesized e.g. by the
BKL conjecture). The
cosmic censorship hypothesis The weak and the strong cosmic censorship hypotheses are two mathematical conjectures about the structure of gravitational singularities arising in general relativity.
Singularities that arise in the solutions of Einstein's equations are typically ...
states that all realistic future singularities (no perfect symmetries, matter with realistic properties) are safely hidden away behind a horizon, and thus invisible to all distant observers. While no formal proof yet exists, numerical simulations offer supporting evidence of its validity.
Evolution equations
Each solution of Einstein's equation encompasses the whole history of a universe—it is not just some snapshot of how things are, but a whole, possibly matter-filled, spacetime. It describes the state of matter and geometry everywhere and at every moment in that particular universe. Due to its general covariance, Einstein's theory is not sufficient by itself to determine the
time evolution
Time evolution is the change of state brought about by the passage of time, applicable to systems with internal state (also called ''stateful systems''). In this formulation, ''time'' is not required to be a continuous parameter, but may be disc ...
of the metric tensor. It must be combined with a
coordinate condition, which is analogous to
gauge fixing
In the physics of gauge theory, gauge theories, gauge fixing (also called choosing a gauge) denotes a mathematical procedure for coping with redundant Degrees of freedom (physics and chemistry), degrees of freedom in field (physics), field variab ...
in other field theories.
To understand Einstein's equations as partial differential equations, it is helpful to formulate them in a way that describes the evolution of the universe over time. This is done in "3+1" formulations, where spacetime is split into three space dimensions and one time dimension. The best-known example is the
ADM formalism
The ADM formalism (named for its authors Richard Arnowitt, Stanley Deser and Charles W. Misner) is a Hamiltonian formulation of general relativity that plays an important role in canonical quantum gravity and numerical relativity. It was fir ...
. These decompositions show that the spacetime evolution equations of general relativity are well-behaved: solutions always
exist
eXist-db (or eXist for short) is an open source software project for NoSQL databases built on XML technology. It is classified as both a NoSQL document-oriented database system and a native XML database (and it provides support for XML, JSON, HT ...
, and are uniquely defined, once suitable initial conditions have been specified. Such formulations of Einstein's field equations are the basis of numerical relativity.
Global and quasi-local quantities
The notion of evolution equations is intimately tied in with another aspect of general relativistic physics. In Einstein's theory, it turns out to be impossible to find a general definition for a seemingly simple property such as a system's total mass (or energy). The main reason is that the gravitational field—like any physical field—must be ascribed a certain energy, but that it proves to be fundamentally impossible to localize that energy.
Nevertheless, there are possibilities to define a system's total mass, either using a hypothetical "infinitely distant observer" (
ADM mass) or suitable symmetries (
Komar mass). If one excludes from the system's total mass the energy being carried away to infinity by gravitational waves, the result is the
Bondi mass at null infinity. Just as in
classical physics, it can be shown that these masses are positive. Corresponding global definitions exist for momentum and angular momentum. There have also been a number of attempts to define ''quasi-local'' quantities, such as the mass of an isolated system formulated using only quantities defined within a finite region of space containing that system. The hope is to obtain a quantity useful for general statements about
isolated system
In physical science, an isolated system is either of the following:
# a physical system so far removed from other systems that it does not interact with them.
# a thermodynamic system enclosed by rigid immovable walls through which neither m ...
s, such as a more precise formulation of the hoop conjecture.
Relationship with quantum theory
If general relativity were considered to be one of the two pillars of modern physics, then quantum theory, the basis of understanding matter from elementary particles to
solid-state physics
Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the l ...
, would be the other. However, how to reconcile quantum theory with general relativity is still an open question.
Quantum field theory in curved spacetime
Ordinary
quantum field theories, which form the basis of modern elementary particle physics, are defined in flat Minkowski space, which is an excellent approximation when it comes to describing the behavior of microscopic particles in weak gravitational fields like those found on Earth. In order to describe situations in which gravity is strong enough to influence (quantum) matter, yet not strong enough to require quantization itself, physicists have formulated quantum field theories in curved spacetime. These theories rely on general relativity to describe a curved background spacetime, and define a generalized quantum field theory to describe the behavior of quantum matter within that spacetime. Using this formalism, it can be shown that black holes emit a blackbody spectrum of particles known as
Hawking radiation
Hawking radiation is theoretical black body radiation that is theorized to be released outside a black hole's event horizon because of relativistic quantum effects. It is named after the physicist Stephen Hawking, who developed a theoretical ar ...
leading to the possibility that they
evaporate
Evaporation is a type of vaporization that occurs on the surface of a liquid as it changes into the gas phase. High concentration of the evaporating substance in the surrounding gas significantly slows down evaporation, such as when humid ...
over time. As briefly mentioned
above, this radiation plays an important role for the thermodynamics of black holes.
Quantum gravity
The demand for consistency between a quantum description of matter and a geometric description of spacetime, as well as the appearance of singularities (where curvature length scales become microscopic), indicate the need for a full theory of quantum gravity: for an adequate description of the interior of black holes, and of the very early universe, a theory is required in which gravity and the associated geometry of spacetime are described in the language of quantum physics. Despite major efforts, no complete and consistent theory of quantum gravity is currently known, even though a number of promising candidates exist.

Attempts to generalize ordinary quantum field theories, used in elementary particle physics to describe fundamental interactions, so as to include gravity have led to serious problems. Some have argued that at low energies, this approach proves successful, in that it results in an acceptable
effective (quantum) field theory of gravity. At very high energies, however, the perturbative results are badly divergent and lead to models devoid of predictive power ("perturbative
non-renormalizability").

One attempt to overcome these limitations is
string theory, a quantum theory not of
point particle
A point particle (ideal particle or point-like particle, often spelled pointlike particle) is an idealization of particles heavily used in physics. Its defining feature is that it lacks spatial extension; being dimensionless, it does not take u ...
s, but of minute one-dimensional extended objects. The theory promises to be a
unified description of all particles and interactions, including gravity; the price to pay is unusual features such as six
extra dimensions
In physics, extra dimensions are proposed additional space or time dimensions beyond the (3 + 1) typical of observed spacetime, such as the first attempts based on the Kaluza–Klein theory. Among theories proposing extra dimensions are: ...
of space in addition to the usual three. In what is called the
second superstring revolution
The history of string theory spans several decades of intense research including two superstring revolutions. Through the combined efforts of many researchers, string theory has developed into a broad and varied subject with connections to quantu ...
, it was conjectured that both string theory and a unification of general relativity and
supersymmetry
In a supersymmetric theory the equations for force and the equations for matter are identical. In theoretical and mathematical physics, any theory with this property has the principle of supersymmetry (SUSY). Dozens of supersymmetric theories e ...
known as
supergravity
In theoretical physics, supergravity (supergravity theory; SUGRA for short) is a modern field theory that combines the principles of supersymmetry and general relativity; this is in contrast to non-gravitational supersymmetric theories such as ...
form part of a hypothesized eleven-dimensional model known as
M-theory
M-theory is a theory in physics that unifies all consistent versions of superstring theory. Edward Witten first conjectured the existence of such a theory at a string theory conference at the University of Southern California in 1995. Witte ...
, which would constitute a uniquely defined and consistent theory of quantum gravity.
Another approach starts with the
canonical quantization
In physics, canonical quantization is a procedure for quantizing a classical theory, while attempting to preserve the formal structure, such as symmetries, of the classical theory, to the greatest extent possible.
Historically, this was not quit ...
procedures of quantum theory. Using the initial-value-formulation of general relativity (cf.
evolution equations above), the result is the
Wheeler–deWitt equation
The Wheeler–DeWitt equation for theoretical physics and applied mathematics, is a field equation attributed to John Archibald Wheeler and Bryce DeWitt. The equation attempts to mathematically combine the ideas of quantum mechanics and general ...
(an analogue of the
Schrödinger equation
The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of th ...
) which, regrettably, turns out to be ill-defined without a proper ultraviolet (lattice) cutoff. However, with the introduction of what are now known as
Ashtekar variables, this leads to a promising model known as
loop quantum gravity
Loop quantum gravity (LQG) is a theory of quantum gravity, which aims to merge quantum mechanics and general relativity, incorporating matter of the Standard Model into the framework established for the pure quantum gravity case. It is an attem ...
. Space is represented by a web-like structure called a
spin network
In physics, a spin network is a type of diagram which can be used to represent states and interactions between particles and fields in quantum mechanics. From a mathematical perspective, the diagrams are a concise way to represent multiline ...
, evolving over time in discrete steps.
Depending on which features of general relativity and quantum theory are accepted unchanged, and on what level changes are introduced, there are numerous other attempts to arrive at a viable theory of quantum gravity, some examples being the lattice theory of gravity based on the Feynman
Path Integral approach and
Regge calculus In general relativity, Regge calculus is a formalism for producing simplicial approximations of spacetimes that are solutions to the Einstein field equation. The calculus was introduced by the Italian theoretician Tullio Regge in 1961. Available ...
,
,
causal sets, twistor models or the path integral based models of
quantum cosmology
Quantum cosmology is the attempt in theoretical physics to develop a quantum theory of the universe. This approach attempts to answer open questions of classical physical cosmology, particularly those related to the first phases of the universe. ...
.
All candidate theories still have major formal and conceptual problems to overcome. They also face the common problem that, as yet, there is no way to put quantum gravity predictions to experimental tests (and thus to decide between the candidates where their predictions vary), although there is hope for this to change as future data from cosmological observations and particle physics experiments becomes available.
Current status

General relativity has emerged as a highly successful model of gravitation and cosmology, which has so far passed many unambiguous observational and experimental tests. However, there are strong indications that the theory is incomplete. The problem of quantum gravity and the question of the reality of spacetime singularities remain open. Observational data that is taken as evidence for dark energy and dark matter could indicate the need for new physics. Even taken as is, general relativity is rich with possibilities for further exploration. Mathematical relativists seek to understand the nature of singularities and the fundamental properties of Einstein's equations, while numerical relativists run increasingly powerful computer simulations (such as those describing merging black holes). In February 2016, it was announced that the existence of gravitational waves was directly detected by the Advanced LIGO team on 14 September 2015.
A century after its introduction, general relativity remains a highly active area of research.
[See, e.g., the '']Living Reviews in Relativity
''Living Reviews in Relativity'' is a peer-reviewed open-access scientific journal publishing reviews on relativity in the areas of physics and astrophysics. It was founded by Bernard Schutz and published at the Max Planck Institute for Gravi ...
'' journal.
See also
*
Alcubierre drive
The Alcubierre drive () is a speculative warp drive idea according to which a spacecraft could achieve apparent faster-than-light travel by contracting space in front of it and expanding space behind it, under the assumption that a configurable ...
(warp drive)
*
Alternatives to general relativity
*
Center of mass (relativistic)
*
Contributors to general relativity
*
Derivations of the Lorentz transformations
*
Ehrenfest paradox
The Ehrenfest paradox concerns the rotation of a "rigid" disc in the theory of relativity.
In its original 1909 formulation as presented by Paul Ehrenfest in relation to the concept of Born rigidity within special relativity, it discusses an ide ...
*
Einstein–Hilbert action
The Einstein–Hilbert action (also referred to as Hilbert action) in general relativity is the action that yields the Einstein field equations through the stationary-action principle. With the metric signature, the gravitational part of the act ...
*
Einstein's thought experiments
*
General relativity priority dispute
*
Introduction to the mathematics of general relativity
*
Nordström's theory of gravitation
In theoretical physics, Nordström's theory of gravitation was a predecessor of general relativity. Strictly speaking, there were actually ''two'' distinct theories proposed by the Finnish theoretical physicist Gunnar Nordström, in 1912 and 19 ...
*
Ricci calculus
In mathematics, Ricci calculus constitutes the rules of index notation and manipulation for tensors and tensor fields on a differentiable manifold, with or without a metric tensor or connection. It is also the modern name for what used to b ...
*
Tests of general relativity
Tests of general relativity serve to establish observational evidence for the theory of general relativity. The first three tests, proposed by Albert Einstein in 1915, concerned the "anomalous" precession of the perihelion of Mercury (planet), Me ...
*
Timeline of gravitational physics and relativity
The following is a timeline of gravitational physics and general relativity.
Before 1500
* 3rd century BC - Aristarchus of Samos proposes heliocentric model, measures the distance to the Moon and its size
1500s
* 1543 – Nicolaus Copernicus p ...
*
Two-body problem in general relativity
The two-body problem in general relativity is the determination of the motion and gravitational field of two bodies as described by the field equations of general relativity. Solving the Kepler problem is essential to calculate the bending of l ...
*
Weak Gravity Conjecture
References
Bibliography
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
* ; original paper in Russian:
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
* See als
English translation at Einstein Papers Project
* See als
English translation at Einstein Papers Project* See als
English translation at Einstein Papers Project*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
Further reading
Popular books
*
*
*
*
*
*
*
Beginning undergraduate textbooks
*
*
Advanced undergraduate textbooks
*
*
*
*
*
*
*
*
*
*
Graduate textbooks
*
*
*
*
*
*
*
Wald, Robert (1984). ''General Relativity''. University of Chicago Press.
ISBN
The International Standard Book Number (ISBN) is a numeric commercial book identifier that is intended to be unique. Publishers purchase ISBNs from an affiliate of the International ISBN Agency.
An ISBN is assigned to each separate edition an ...
978-0226870335.
Specialists' books
*
*
Journal articles
* See als
English translation at Einstein Papers Project*
*
*
*
*
External links
Einstein Online – Articles on a variety of aspects of relativistic physics for a general audience; hosted by the
Max Planck Institute for Gravitational Physics
The Max Planck Institute for Gravitational Physics (Albert Einstein Institute) is a Max Planck Institute whose research is aimed at investigating Einstein's theory of relativity and beyond: Mathematics, quantum gravity, astrophysical relativity, ...
GEO600 home page the official website of the GEO600 project.
LIGO Laboratory
nbsp;– produced by the numerical relativity group at the NCSA, with an elementary introduction to general relativity
* (lecture by Leonard Susskind
Leonard Susskind (; born June 16, 1940)his 60th birthday was celebrated with a special symposium at Stanford University.in Geoffrey West's introduction, he gives Suskind's current age as 74 and says his birthday was recent. is an American physicis ...
recorded 22 September 2008 at Stanford University).
Series of lectures on General Relativity
given in 2006 at the Institut Henri Poincaré (introductory/advanced).
General Relativity Tutorials
by John Baez
John Carlos Baez (; born June 12, 1961) is an American mathematical physicist and a professor of mathematics at the University of California, Riverside (UCR) in Riverside, California. He has worked on spin foams in loop quantum gravity, appl ...
.
*
*
*
*
The Feynman Lectures on Physics Vol. II Ch. 42: Curved Space
{{Featured article
Concepts in astronomy
Albert Einstein
1915 in science
Articles containing video clips
 Assuming that the equivalence principle holds, gravity influences the passage of time. Light sent down into a
Assuming that the equivalence principle holds, gravity influences the passage of time. Light sent down into a  General relativity predicts that the path of light will follow the curvature of spacetime as it passes near a star. This effect was initially confirmed by observing the light of stars or distant quasars being deflected as it passes the
General relativity predicts that the path of light will follow the curvature of spacetime as it passes near a star. This effect was initially confirmed by observing the light of stars or distant quasars being deflected as it passes the  Predicted in 1916 by Albert Einstein, there are gravitational waves: ripples in the metric of spacetime that propagate at the speed of light. These are one of several analogies between weak-field gravity and electromagnetism in that, they are analogous to
Predicted in 1916 by Albert Einstein, there are gravitational waves: ripples in the metric of spacetime that propagate at the speed of light. These are one of several analogies between weak-field gravity and electromagnetism in that, they are analogous to  According to general relativity, a binary system will emit gravitational waves, thereby losing energy. Due to this loss, the distance between the two orbiting bodies decreases, and so does their orbital period. Within the
According to general relativity, a binary system will emit gravitational waves, thereby losing energy. Due to this loss, the distance between the two orbiting bodies decreases, and so does their orbital period. Within the  The deflection of light by gravity is responsible for a new class of astronomical phenomena. If a massive object is situated between the astronomer and a distant target object with appropriate mass and relative distances, the astronomer will see multiple distorted images of the target. Such effects are known as gravitational lensing. Depending on the configuration, scale, and mass distribution, there can be two or more images, a bright ring known as an
The deflection of light by gravity is responsible for a new class of astronomical phenomena. If a massive object is situated between the astronomer and a distant target object with appropriate mass and relative distances, the astronomer will see multiple distorted images of the target. Such effects are known as gravitational lensing. Depending on the configuration, scale, and mass distribution, there can be two or more images, a bright ring known as an  Observations of binary pulsars provide strong indirect evidence for the existence of gravitational waves (see
Observations of binary pulsars provide strong indirect evidence for the existence of gravitational waves (see  Whenever the ratio of an object's mass to its radius becomes sufficiently large, general relativity predicts the formation of a black hole, a region of space from which nothing, not even light, can escape. In the currently accepted models of
Whenever the ratio of an object's mass to its radius becomes sufficiently large, general relativity predicts the formation of a black hole, a region of space from which nothing, not even light, can escape. In the currently accepted models of  The current models of cosmology are based on Einstein's field equations, which include the cosmological constant since it has important influence on the large-scale dynamics of the cosmos,
:
where '''' is the spacetime metric. Isotropic and homogeneous solutions of these enhanced equations, the Friedmann–Lemaître–Robertson–Walker solutions, allow physicists to model a universe that has evolved over the past 14
The current models of cosmology are based on Einstein's field equations, which include the cosmological constant since it has important influence on the large-scale dynamics of the cosmos,
:
where '''' is the spacetime metric. Isotropic and homogeneous solutions of these enhanced equations, the Friedmann–Lemaître–Robertson–Walker solutions, allow physicists to model a universe that has evolved over the past 14  Attempts to generalize ordinary quantum field theories, used in elementary particle physics to describe fundamental interactions, so as to include gravity have led to serious problems. Some have argued that at low energies, this approach proves successful, in that it results in an acceptable effective (quantum) field theory of gravity. At very high energies, however, the perturbative results are badly divergent and lead to models devoid of predictive power ("perturbative non-renormalizability").
Attempts to generalize ordinary quantum field theories, used in elementary particle physics to describe fundamental interactions, so as to include gravity have led to serious problems. Some have argued that at low energies, this approach proves successful, in that it results in an acceptable effective (quantum) field theory of gravity. At very high energies, however, the perturbative results are badly divergent and lead to models devoid of predictive power ("perturbative non-renormalizability").