|
Charged Black Hole
A charged black hole is a black hole that possesses electric charge. Since the electromagnetic repulsion in compressing an electrically charged mass is dramatically greater than the gravitational attraction (by about 40 orders of magnitude), it is not expected that black holes with a significant electric charge will be formed in nature. Categories The two types of charged black holes are Reissner–Nordström black holes (without spin) and Kerr–Newman black holes (with spin). A black hole can be completely characterized by three ( and only three) quantities: * ''M'' – mass * ''J'' – angular momentum * ''Q'' – electric charge Charged black holes are two of four possible types of black holes that have been found by solving Einstein's theory of gravitation, general relativity. The mathematical solutions for the shape of space and the electric and magnetic fields near a black hole are named after the persons who first worked them out. The solutions increase in complexity de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Black Hole
A black hole is a region of spacetime where gravity is so strong that nothing, including light or other electromagnetic waves, has enough energy to escape it. The theory of general relativity predicts that a sufficiently compact mass can deform spacetime to form a black hole. The boundary of no escape is called the event horizon. Although it has a great effect on the fate and circumstances of an object crossing it, it has no locally detectable features according to general relativity. In many ways, a black hole acts like an ideal black body, as it reflects no light. Moreover, quantum field theory in curved spacetime predicts that event horizons emit Hawking radiation, with the same spectrum as a black body of a temperature inversely proportional to its mass. This temperature is of the order of billionths of a kelvin for stellar black holes, making it essentially impossible to observe directly. Objects whose gravitational fields are too strong for light to escape were fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
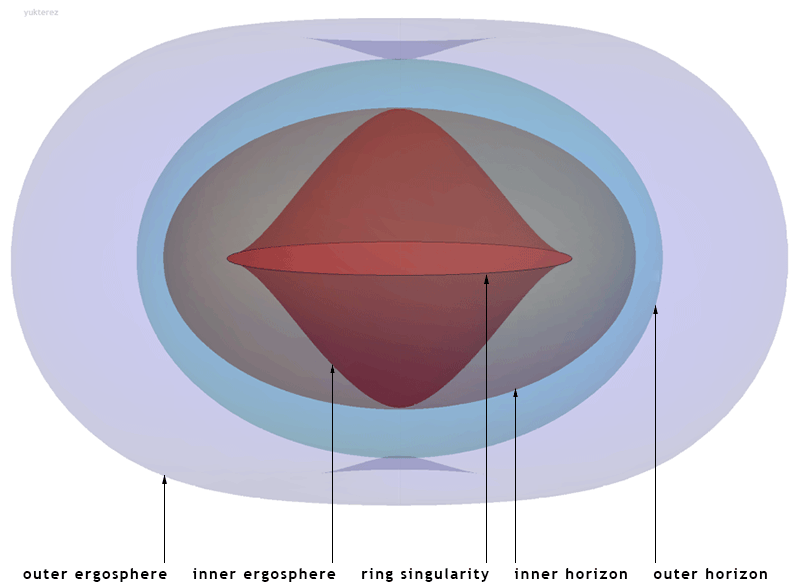
Kerr Black Hole
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find. Overview The Kerr metric is a generalization to a rotating body of the Schwarzschild metric, discovered by Karl Schwarzschild in 1915, which described the geometry of spacetime around an uncharged, spherically symmetric, and non-rotating body. The corresponding solution for a ''charged'', spherical, non-rotating body, the Reissner–Nordström metric, was discovered soon afterwards (1916–1918). However, the exact solution for an uncharged, ''rotating'' black hole, the Kerr metric, remained unsolved until 1963, when it was discovered by Roy Kerr.Melia, Fulvio (2009). "Cracking the Einstein code: relativity and the birth of b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schwarzschild Metric
In Einstein's theory of general relativity, the Schwarzschild metric (also known as the Schwarzschild solution) is an exact solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assumption that the electric charge of the mass, angular momentum of the mass, and universal cosmological constant are all zero. The solution is a useful approximation for describing slowly rotating astronomical objects such as many stars and planets, including Earth and the Sun. It was found by Karl Schwarzschild in 1916, and around the same time independently by Johannes Droste, who published his more complete and modern-looking discussion four months after Schwarzschild. According to Birkhoff's theorem, the Schwarzschild metric is the most general spherically symmetric vacuum solution of the Einstein field equations. A Schwarzschild black hole or static black hole is a black hole that has neither electric charge nor angular momentum. A Sch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Karl Schwarzschild
Karl Schwarzschild (; 9 October 1873 – 11 May 1916) was a German physicist and astronomer. Schwarzschild provided the first exact solution to the Einstein field equations of general relativity, for the limited case of a single spherical non-rotating mass, which he accomplished in 1915, the same year that Einstein first introduced general relativity. The Schwarzschild solution, which makes use of Schwarzschild coordinates and the Schwarzschild metric, leads to a derivation of the Schwarzschild radius, which is the size of the event horizon of a non-rotating black hole. Schwarzschild accomplished this while serving in the German army during World War I. He died the following year from the autoimmune disease pemphigus, which he developed while at the Russian front. Various forms of the disease particularly affect people of Ashkenazi Jewish origin. Asteroid 837 Schwarzschilda is named in his honour, as is the large crater ''Schwarzschild'', on the far side of the Moon. L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gunnar Nordström
Gunnar Nordström (12 March 1881 – 24 December 1923) was a Finland, Finnish theoretical physicist best remembered for Nordström's theory of gravitation, his theory of gravitation, which was an early competitor of general relativity. Nordström is often designated by modern writers as ''The Einstein of Finland'' due to his novel work in similar fields with similar methods to Einstein.Raimo Keskinen (1981): Gunnar Nordström 1881B1923. Arkhimedes 2/1981, s. 71B84. In Finnish, excerpt http://www.tieteessatapahtuu.fi/797/KESKINEN.pdf Education and career Nordström graduated high-school from ''Brobergska skolan'' in central Helsinki 1899. At first he went on to study mechanical engineering, graduating in 1903 from the Helsinki University of Technology, Polytechnic institute in Helsinki, later renamed Helsinki University of Technology and today a part of the Aalto University. During his studies he developed an interest for more theoretical subjects, proceeding after graduation to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hans Reissner
Hans Jacob Reissner, also known as Jacob Johannes Reissner (18 January 1874, Berlin – 2 October 1967, Mt. Angel, Oregon), was a German aeronautical engineer whose avocation was mathematical physics. During World War I he was awarded the Iron Cross second class (for civilians) for his pioneering work on aircraft design. Biography Reissner was born into a wealthy Berlin family that benefited from an inheritance from his great-uncle on his mother's side. As a young engineering graduate, he spent a year in the U.S. working as a draftsman. After this year, he broadened his academic interests to include physics. As a young academic, he published mathematical papers on engineering problems. Before the first World War, Reissner designed the first successful all-metal aircraft, the Reissner Canard (or Ente) with both skin and structure made of metal. This was constructed with assistance from Hugo Junkers who had previously shown little interest in aviation. Both were professors a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravitational Field
In physics, a gravitational field is a model used to explain the influences that a massive body extends into the space around itself, producing a force on another massive body. Thus, a gravitational field is used to explain gravitational phenomena, and is measured in newtons per kilogram (N/kg). Equivalently, it is measured in meters per second squared (m/s2). In its original concept, gravity was a force between point masses. Following Isaac Newton, Pierre-Simon Laplace attempted to model gravity as some kind of radiation field or fluid, and since the 19th century, explanations for gravity have usually been taught in terms of a field model, rather than a point attraction. In a field model, rather than two particles attracting each other, the particles distort spacetime via their mass, and this distortion is what is perceived and measured as a "force". In such a model one states that matter moves in certain ways in response to the curvature of spacetime, and that th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstein's Field Equation
In the general theory of relativity, the Einstein field equations (EFE; also known as Einstein's equations) relate the geometry of spacetime to the distribution of matter within it. The equations were published by Einstein in 1915 in the form of a tensor equation which related the local ' (expressed by the Einstein tensor) with the local energy, momentum and stress within that spacetime (expressed by the stress–energy tensor). Analogously to the way that electromagnetic fields are related to the distribution of charges and currents via Maxwell's equations, the EFE relate the spacetime geometry to the distribution of mass–energy, momentum and stress, that is, they determine the metric tensor of spacetime for a given arrangement of stress–energy–momentum in the spacetime. The relationship between the metric tensor and the Einstein tensor allows the EFE to be written as a set of nonlinear partial differential equations when used in this way. The solutions of the EFE ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schwarzschild Black Hole
In Einstein's theory of general relativity, the Schwarzschild metric (also known as the Schwarzschild solution) is an exact solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assumption that the electric charge of the mass, angular momentum of the mass, and universal cosmological constant are all zero. The solution is a useful approximation for describing slowly rotating astronomical objects such as many stars and planets, including Earth and the Sun. It was found by Karl Schwarzschild in 1916, and around the same time independently by Johannes Droste, who published his more complete and modern-looking discussion four months after Schwarzschild. According to Birkhoff's theorem, the Schwarzschild metric is the most general spherically symmetric vacuum solution of the Einstein field equations. A Schwarzschild black hole or static black hole is a black hole that has neither electric charge nor angular momentum. A Schwa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Charge
Electric charge is the physical property of matter that causes charged matter to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative'' (commonly carried by protons and electrons respectively). Like charges repel each other and unlike charges attract each other. An object with an absence of net charge is referred to as neutral. Early knowledge of how charged substances interact is now called classical electrodynamics, and is still accurate for problems that do not require consideration of quantum effects. Electric charge is a conserved property; the net charge of an isolated system, the amount of positive charge minus the amount of negative charge, cannot change. Electric charge is carried by subatomic particles. In ordinary matter, negative charge is carried by electrons, and positive charge is carried by the protons in the nuclei of atoms. If there are more electrons than protons in a piece of matter, it will have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time or four-dimensional spacetime. In particular, the ' is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of second order partial differential equations. Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Momentum
In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity—the total angular momentum of a closed system remains constant. Angular momentum has both a direction and a magnitude, and both are conserved. Bicycles and motorcycles, frisbees, rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it. The three-dimensional angular momentum for a point particle is classically represented as a pseudovector , the cross product of the particle's position vector (relative to some origin) and its momentum vector; the latter is in Newtonian mechanics. Unlike linear momentum, angular mome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |