Schläfli-Hess Polytope on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 The Schläfli–Hess 4-polytopes are the complete set of 10 regular self-intersecting star polychora ( four-dimensional polytopes).Coxeter, ''Star polytopes and the Schläfli function f{α,β,γ)'' p. 122 2. ''The Schläfli-Hess polytopes'' They are named in honor of their discoverers:
The Schläfli–Hess 4-polytopes are the complete set of 10 regular self-intersecting star polychora ( four-dimensional polytopes).Coxeter, ''Star polytopes and the Schläfli function f{α,β,γ)'' p. 122 2. ''The Schläfli-Hess polytopes'' They are named in honor of their discoverers:
Conway (abbrev.) ! Orthogonal
projection ! Schläfli
{p, q} ! F
{p} ! E
{r} ! V
{q, r} ! Dens. ! χ , - align=center BGCOLOR="#e0e0ff" ,
polyicosahedron (pI) , , {3,5,5/2}
, {3,5,5/2}
, 120
{3,5}
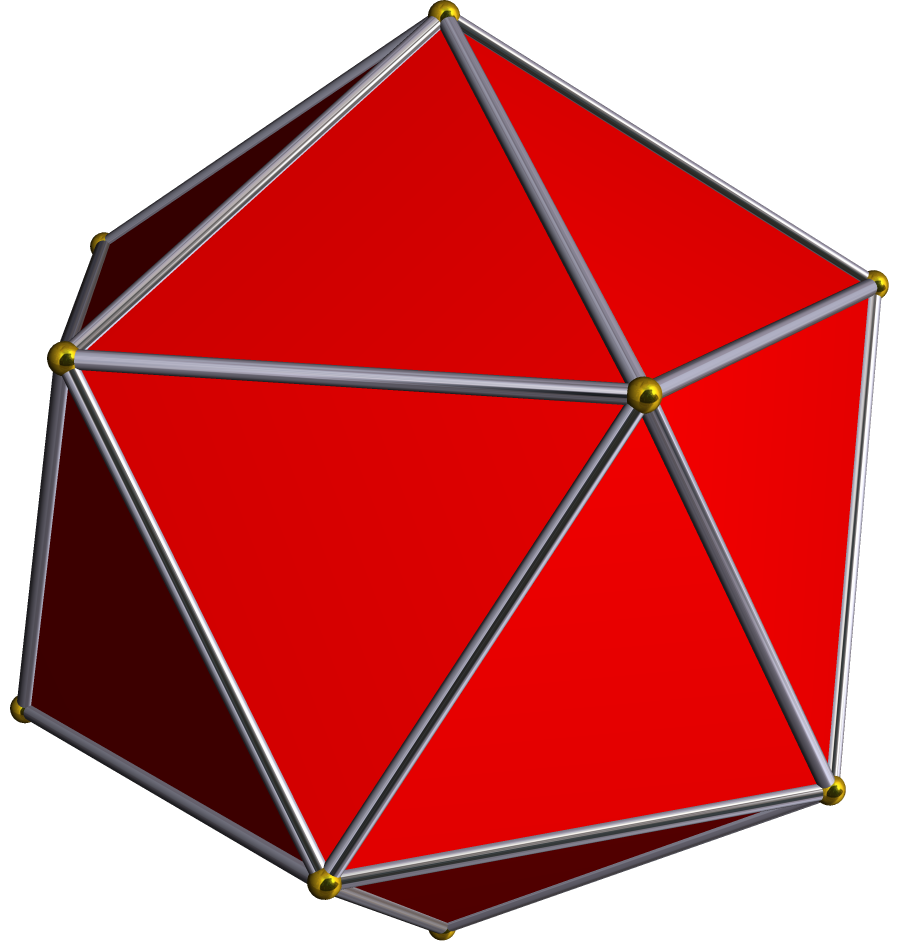 , 1200
, 1200
{3}
 , 720
, 720
{5/2}
 , 120
, 120
{5,5/2}
 , 4
, 480
, - align=center BGCOLOR="#ffe0e0"
,
, 4
, 480
, - align=center BGCOLOR="#ffe0e0"
,
stellated polydodecahedron (spD) , , {5/2,5,3}
, {5/2,5,3}
, 120
{5/2,5}
 , 720
, 720
{5/2}
 , 1200
, 1200
{3}
 , 120
, 120
{5,3}
 , 4
, −480
, - align=center BGCOLOR="#e0ffe0"
,
, 4
, −480
, - align=center BGCOLOR="#e0ffe0"
,
great polydodecahedron (gpD) , , {5,5/2,5}
, {5,5/2,5}
, 120
{5,5/2}
 , 720
, 720
{5}
 , 720
, 720
{5}
 , 120
, 120
{5/2,5}
 , 6
, 0
, - align=center BGCOLOR="#e0e0ff"
,
, 6
, 0
, - align=center BGCOLOR="#e0e0ff"
,
grand polydodecahedron (apD) , , {5,3,5/2}
, {5,3,5/2}
, 120
{5,3}
 , 720
, 720
{5}
 , 720
, 720
{5/2}
 , 120
, 120
{3,5/2}
 , 20
, 0
, - align=center BGCOLOR="#ffe0e0"
,
, 20
, 0
, - align=center BGCOLOR="#ffe0e0"
,
great stellated polydodecahedron (gspD) , , {5/2,3,5}
, {5/2,3,5}
, 120
{5/2,3}
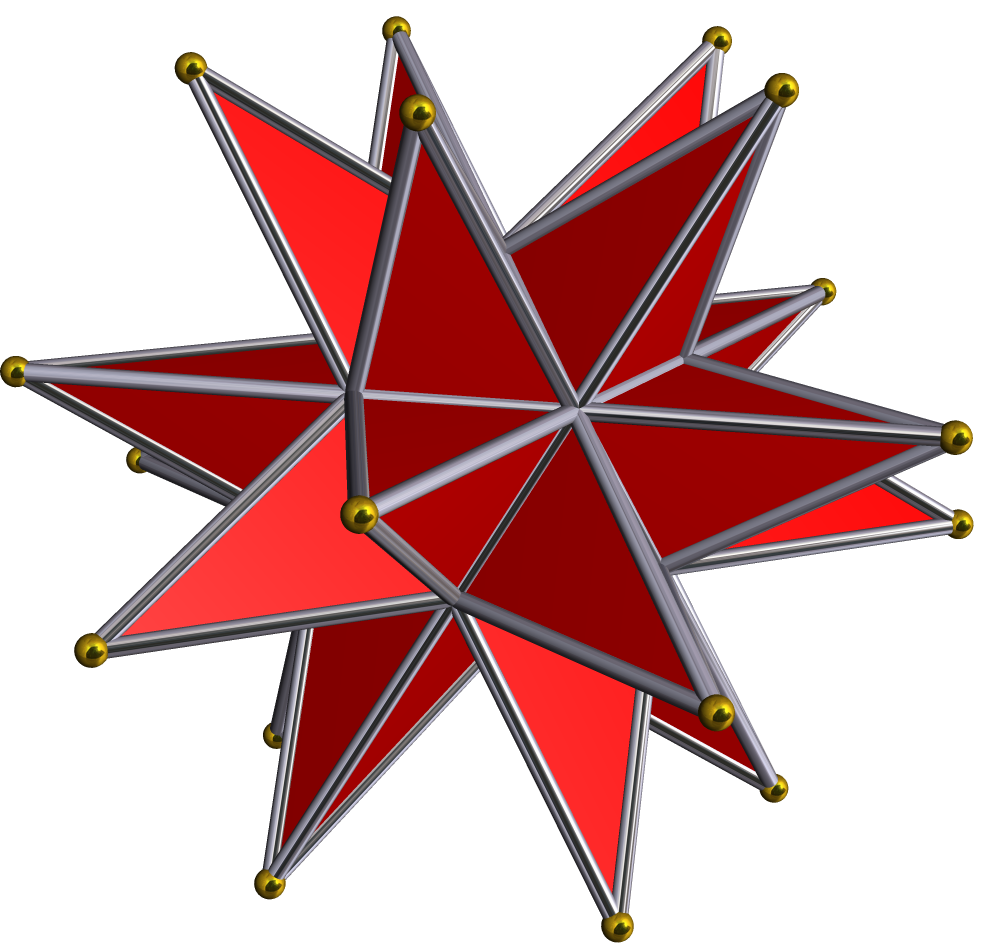 , 720
, 720
{5/2}
 , 720
, 720
{5}
 , 120
, 120
{3,5}
 , 20
, 0
, - align=center BGCOLOR="#e0ffe0"
,
, 20
, 0
, - align=center BGCOLOR="#e0ffe0"
,
grand stellated polydodecahedron (aspD) , , {5/2,5,5/2}
, {5/2,5,5/2}
, 120
{5/2,5}
 , 720
, 720
{5/2}
 , 720
, 720
{5/2}
 , 120
, 120
{5,5/2}
 , 66
, 0
, - align=center BGCOLOR="#e0e0ff"
,
, 66
, 0
, - align=center BGCOLOR="#e0e0ff"
,
great grand polydodecahedron (gapD) , , {5,5/2,3}
, {5,5/2,3}
, 120
{5,5/2}
 , 720
, 720
{5}
 , 1200
, 1200
{3}
 , 120
, 120
{5/2,3}
 , 76
, −480
, - align=center BGCOLOR="#ffe0e0"
,
, 76
, −480
, - align=center BGCOLOR="#ffe0e0"
,
great polyicosahedron (gpI) , , {3,5/2,5}
, {3,5/2,5}
, 120
{3,5/2}
 , 1200
, 1200
{3}
 , 720
, 720
{5}
 , 120
, 120
{5/2,5}
 , 76
, 480
, - align=center BGCOLOR="#e0e0ff"
,
, 76
, 480
, - align=center BGCOLOR="#e0e0ff"
,
grand polytetrahedron (apT) , , {3,3,5/2}
, {3,3,5/2}
, 600
{3,3}
 , 1200
, 1200
{3}
 , 720
, 720
{5/2}
 , 120
, 120
{3,5/2}
 , 191
, 0
, - align=center BGCOLOR="#ffe0e0"
,
, 191
, 0
, - align=center BGCOLOR="#ffe0e0"
,
great grand stellated polydodecahedron (gaspD) , , {5/2,3,3}
, {5/2,3,3}
, 120
{5/2,3}
 , 720
, 720
{5/2}
 , 1200
, 1200
{3}
 , 600
, 600
{3,3}
 , 191
, 0
, 191
, 0
Jonathan Bowers, 16 regular 4-polytopesRegular 4D Polytope Foldouts
A collection of stereographic projections of 4-polytopes.
A Catalog of Uniform PolytopesDimensions
2 hour film about the fourth dimension (contains stereographic projections of all regular 4-polytopes)
Reguläre Polytope
{{DEFAULTSORT:Regular 4-polytope 4-polytopes
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, a regular 4-polytope is a regular four-dimensional polytope. They are the four-dimensional analogues of the regular polyhedra
A regular polyhedron is a polyhedron whose symmetry group acts transitively on its flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different equival ...
in three dimensions and the regular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either convex p ...
s in two dimensions.
There are six convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytope ...
and ten star
A star is an astronomical object comprising a luminous spheroid of plasma (physics), plasma held together by its gravity. The List of nearest stars and brown dwarfs, nearest star to Earth is the Sun. Many other stars are visible to the naked ...
regular 4-polytopes, giving a total of sixteen.
History
The convex regular 4-polytopes were first described by the Swissmathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems.
Mathematicians are concerned with numbers, data, quantity, structure, space, models, and change.
History
On ...
Ludwig Schläfli
Ludwig Schläfli (15 January 1814 – 20 March 1895) was a Swiss mathematician, specialising in geometry and complex analysis (at the time called function theory) who was one of the key figures in developing the notion of higher-dimensional space ...
in the mid-19th century. He discovered that there are precisely six such figures.
Schläfli also found four of the regular star 4-polytopes: the grand 120-cell
In geometry, the grand 120-cell or grand polydodecahedron is a regular star 4-polytope with Schläfli symbol . It is one of 10 regular Schläfli-Hess polytopes.
It is one of four ''regular star 4-polytopes'' discovered by Ludwig Schläfli. It is n ...
, great stellated 120-cell
In geometry, the great stellated 120-cell or great stellated polydodecahedron is a regular star 4-polytope with Schläfli symbol . It is one of 10 regular Schläfli-Hess polytopes.
It is one of four ''regular star 4-polytopes'' discovered by Lud ...
, grand 600-cell
In geometry, the grand 600-cell or grand polytetrahedron is a regular star 4-polytope with Schläfli symbol . It is one of 10 regular Schläfli-Hess polytopes. It is the only one with 600 cells.
It is one of four ''regular star 4-polytopes'' disc ...
, and great grand stellated 120-cell
In geometry, the great grand stellated 120-cell or great grand stellated polydodecahedron is a regular star 4-polytope with Schläfli symbol , one of 10 regular Schläfli-Hess 4-polytopes. It is unique among the 10 for having 600 vertices, and ha ...
. He skipped the remaining six because he would not allow forms that failed the Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space ...
on cells or vertex figures (for zero-hole tori: ''F'' − ''E'' + ''V'' 2). That excludes cells and vertex figures such as the great dodecahedron
In geometry, the great dodecahedron is a Kepler–Poinsot polyhedron, with Schläfli symbol and Coxeter–Dynkin diagram of . It is one of four nonconvex regular polyhedra. It is composed of 12 pentagonal faces (six pairs of parallel pentagon ...
and small stellated dodecahedron
In geometry, the small stellated dodecahedron is a Kepler-Poinsot polyhedron, named by Arthur Cayley, and with Schläfli symbol . It is one of four nonconvex regular polyhedra. It is composed of 12 pentagrammic faces, with five pentagrams meeti ...
.
Edmund Hess
Edmund Hess (17 February 1843 – 24 December 1903) was a German mathematician who discovered several regular polytopes.
See also
* Schläfli–Hess polychoron
* Hess polytope
References
* ''Regular Polytopes
In mathematics, a regu ...
(1843–1903) published the complete list in his 1883 German book ''Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder''.
Construction
The existence of a regular 4-polytope is constrained by the existence of the regular polyhedra which form its cells and adihedral angle
A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the uni ...
constraint
:
to ensure that the cells meet to form a closed 3-surface.
The six convex and ten star polytopes described are the only solutions to these constraints.
There are four nonconvex Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
s that have valid cells and vertex figures , and pass the dihedral test, but fail to produce finite figures: , , , .
Regular convex 4-polytopes
The regular convex 4-polytopes are the four-dimensional analogues of thePlatonic solid
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all edges c ...
s in three dimensions and the convex regular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either convex p ...
s in two dimensions.
Five of the six are clearly analogues of the five corresponding Platonic solids. The sixth, the 24-cell
In geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, oct ...
, has no regular analogue in three dimensions. However, there exists a pair of irregular solids, the cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it ...
and its dual the rhombic dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron.
Properties
The rhombic dodecahedro ...
, which are partial analogues to the 24-cell (in complementary ways). Together they can be seen as the three-dimensional analogue of the 24-cell.
Each convex regular 4-polytope is bounded by a set of 3-dimensional ''cells
Cell most often refers to:
* Cell (biology), the functional basic unit of life
Cell may also refer to:
Locations
* Monastic cell, a small room, hut, or cave in which a religious recluse lives, alternatively the small precursor of a monastery w ...
'' which are all Platonic solids of the same type and size. These are fitted together along their respective faces (face-to-face) in a regular fashion.
Properties
Like their 3-dimensional analogues, the convex regular 4-polytopes can be naturally ordered by size as a measure of 4-dimensional content (hypervolume) for the same radius. Each greater polytope in the sequence is ''rounder'' than its predecessor, enclosing more content within the same radius. The 4-simplex (5-cell) is the limit smallest case, and the 120-cell is the largest. Complexity (as measured by comparing configuration matrices or simply the number of vertices) follows the same ordering. The following table lists some properties of the six convex regular 4-polytopes. The symmetry groups of these 4-polytopes are allCoxeter group
In mathematics, a Coxeter group, named after H. S. M. Coxeter, is an abstract group that admits a formal description in terms of reflections (or kaleidoscopic mirrors). Indeed, the finite Coxeter groups are precisely the finite Euclidean refl ...
s and given in the notation described in that article. The number following the name of the group is the order
Order, ORDER or Orders may refer to:
* Categorization, the process in which ideas and objects are recognized, differentiated, and understood
* Heterarchy, a system of organization wherein the elements have the potential to be ranked a number of d ...
of the group.
John Conway
John Horton Conway (26 December 1937 – 11 April 2020) was an English mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He also made contributions to many branches o ...
advocated the names simplex, orthoplex, tesseract, octaplex or polyoctahedron (pO), tetraplex or polytetrahedron (pT), and dodecaplex or polydodecahedron (pD).
Norman Johnson advocated the names n-cell, or pentachoron, hexadecachoron, tesseract or octachoron, icositetrachoron, hexacosichoron, and hecatonicosachoron (or dodecacontachoron), coining the term ''polychoron'' being a 4D analogy to the 3D polyhedron, and 2D polygon, expressed from the Greek
Greek may refer to:
Greece
Anything of, from, or related to Greece, a country in Southern Europe:
*Greeks, an ethnic group.
*Greek language, a branch of the Indo-European language family.
**Proto-Greek language, the assumed last common ancestor ...
roots ''poly'' ("many") and ''choros'' ("room" or "space").
The Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space ...
for all 4-polytopes is zero, we have the 4-dimensional analogue of Euler's polyhedral formula:
:
where ''N''''k'' denotes the number of ''k''-faces in the polytope (a vertex is a 0-face, an edge is a 1-face, etc.).
The topology of any given 4-polytope is defined by its Betti number
In algebraic topology, the Betti numbers are used to distinguish topological spaces based on the connectivity of ''n''-dimensional simplicial complexes. For the most reasonable finite-dimensional spaces (such as compact manifolds, finite simplicia ...
s and torsion coefficient
A torsion spring is a spring that works by twisting its end along its axis; that is, a flexible elastic object that stores mechanical energy when it is twisted. When it is twisted, it exerts a torque in the opposite direction, proportional ...
s.
As configurations
A regular 4-polytope can be completely described as a configuration matrix containing counts of its component elements. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers (upper left to lower right) say how many of each element occur in the whole 4-polytope. The non-diagonal numbers say how many of the column's element occur in or at the row's element. For example, there are 2 vertices ''in'' each edge (each edge ''has'' 2 vertices), and 2 cells meet ''at'' each face (each face ''belongs to'' 2 cells), in any regular 4-polytope. Notice that the configuration for the dual polytope can be obtained by rotating the matrix by 180 degrees.Visualization
The following table shows some 2-dimensional projections of these 4-polytopes. Various other visualizations can be found in the external links below. The Coxeter-Dynkin diagram graphs are also given below theSchläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
.
Regular star (Schläfli–Hess) 4-polytopes
 The Schläfli–Hess 4-polytopes are the complete set of 10 regular self-intersecting star polychora ( four-dimensional polytopes).Coxeter, ''Star polytopes and the Schläfli function f{α,β,γ)'' p. 122 2. ''The Schläfli-Hess polytopes'' They are named in honor of their discoverers:
The Schläfli–Hess 4-polytopes are the complete set of 10 regular self-intersecting star polychora ( four-dimensional polytopes).Coxeter, ''Star polytopes and the Schläfli function f{α,β,γ)'' p. 122 2. ''The Schläfli-Hess polytopes'' They are named in honor of their discoverers: Ludwig Schläfli
Ludwig Schläfli (15 January 1814 – 20 March 1895) was a Swiss mathematician, specialising in geometry and complex analysis (at the time called function theory) who was one of the key figures in developing the notion of higher-dimensional space ...
and Edmund Hess
Edmund Hess (17 February 1843 – 24 December 1903) was a German mathematician who discovered several regular polytopes.
See also
* Schläfli–Hess polychoron
* Hess polytope
References
* ''Regular Polytopes
In mathematics, a regu ...
. Each is represented by a Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
{''p'',''q'',''r''} in which one of the numbers is . They are thus analogous to the regular nonconvex Kepler–Poinsot polyhedra, which are in turn analogous to the pentagram.
Names
Their names given here were given byJohn Conway
John Horton Conway (26 December 1937 – 11 April 2020) was an English mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He also made contributions to many branches o ...
, extending Cayley's names for the Kepler–Poinsot polyhedra: along with ''stellated'' and ''great'', he adds a ''grand'' modifier. Conway offered these operational definitions:
#stellation
In geometry, stellation is the process of extending a polygon in two dimensions, polyhedron in three dimensions, or, in general, a polytope in ''n'' dimensions to form a new figure. Starting with an original figure, the process extends specific el ...
– replaces edges by longer edges in same lines. (Example: a pentagon
In geometry, a pentagon (from the Greek πέντε ''pente'' meaning ''five'' and γωνία ''gonia'' meaning ''angle'') is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
A pentagon may be simpl ...
stellates into a pentagram
A pentagram (sometimes known as a pentalpha, pentangle, or star pentagon) is a regular five-pointed star polygon, formed from the diagonal line segments of a convex (or simple, or non-self-intersecting) regular pentagon. Drawing a circle aroun ...
)
#greatening – replaces the faces by large ones in same planes. (Example: an icosahedron
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes and . The plural can be either "icosahedra" () or "icosahedrons".
There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrica ...
greatens into a great icosahedron
In geometry, the great icosahedron is one of four Kepler–Poinsot polyhedra (nonconvex regular polyhedra), with Schläfli symbol and Coxeter-Dynkin diagram of . It is composed of 20 intersecting triangular faces, having five triangles meeti ...
)
#aggrandizement – replaces the cells by large ones in same 3-spaces. (Example: a 600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also known as the C600, hexacosichoron and hexacosihedroid. It is also called a tetraplex (abbreviated from " ...
aggrandizes into a grand 600-cell
In geometry, the grand 600-cell or grand polytetrahedron is a regular star 4-polytope with Schläfli symbol . It is one of 10 regular Schläfli-Hess polytopes. It is the only one with 600 cells.
It is one of four ''regular star 4-polytopes'' disc ...
)
John Conway names the 10 forms from 3 regular celled 4-polytopes: pT=polytetrahedron {3,3,5} (a tetrahedral 600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also known as the C600, hexacosichoron and hexacosihedroid. It is also called a tetraplex (abbreviated from " ...
), pI=polyicoshedron {3,5,} (an icosahedral 120-cell
In geometry, the icosahedral 120-cell, polyicosahedron, faceting, faceted 600-cell or icosaplex is a regular star 4-polytope with Schläfli symbol . It is one of 10 regular Schläfli-Hess polytopes.
It is constructed by 5 icosahedron, icosahedra a ...
), and pD=polydodecahedron {5,3,3} (a dodecahedral 120-cell
In geometry, the 120-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called a C120, dodecaplex (short for "dodecahedral complex"), hyperdodecahedron, polydodecahedron, heca ...
), with prefix modifiers: ''g'', ''a'', and ''s'' for great, (ag)grand, and stellated. The final stellation, the ''great grand stellated polydodecahedron'' contains them all as ''gaspD''.
Symmetry
All ten polychora have ,3,5( H4)hexacosichoric symmetry
In geometry, a point group in four dimensions is an isometry group in four dimensions that leaves the origin fixed, or correspondingly, an isometry group of a 3-sphere.
History on four-dimensional groups
* 1889 Édouard Goursat, ''Sur les subs ...
. They are generated from 6 related Goursat tetrahedra
In geometry, a Goursat tetrahedron is a tetrahedron, tetrahedral fundamental domain of a Wythoff construction. Each tetrahedral face represents a reflection hyperplane on 3-dimensional surfaces: the 3-sphere, Euclidean 3-space, and hyperbolic 3-spa ...
rational-order symmetry groups: ,5,5/2 ,5/2,5 ,3,5/2 /2,5,5/2 ,5/2,3 and ,3,5/2
Each group has 2 regular star-polychora, except for two groups which are self-dual, having only one. So there are 4 dual-pairs and 2 self-dual forms among the ten regular star polychora.
Properties
Note: * There are 2 uniquevertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes.
For example, a ''square vertex arrangement'' is understood to mean four points in a plane, equ ...
s, matching those of the 120-cell
In geometry, the 120-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called a C120, dodecaplex (short for "dodecahedral complex"), hyperdodecahedron, polydodecahedron, heca ...
and 600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also known as the C600, hexacosichoron and hexacosihedroid. It is also called a tetraplex (abbreviated from " ...
.
* There are 4 unique edge arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes.
For example, a ''square vertex arrangement'' is understood to mean four points in a plane, equ ...
s, which are shown as ''wireframes'' orthographic projections
Orthographic projection (also orthogonal projection and analemma) is a means of representing three-dimensional objects in two dimensions. Orthographic projection is a form of parallel projection in which all the projection lines are orthogonal t ...
.
* There are 7 unique face arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes.
For example, a ''square vertex arrangement'' is understood to mean four points in a plane, equ ...
s, shown as ''solids'' (face-colored) orthographic projections.
The cells (polyhedra), their faces (polygons), the ''polygonal edge figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Definitions
Take some corner or vertex of a polyhedron. Mark a point somewhere along each connected edge. Draw lines ...
s'' and ''polyhedral vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connect ...
s'' are identified by their Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
s.
{, class="wikitable sortable"
! NameConway (abbrev.) ! Orthogonal
projection ! Schläfli
Coxeter
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century.
Biography
Coxeter was born in Kensington to ...
! C{p, q} ! F
{p} ! E
{r} ! V
{q, r} ! Dens. ! χ , - align=center BGCOLOR="#e0e0ff" ,
Icosahedral 120-cell
In geometry, the icosahedral 120-cell, polyicosahedron, faceting, faceted 600-cell or icosaplex is a regular star 4-polytope with Schläfli symbol . It is one of 10 regular Schläfli-Hess polytopes.
It is constructed by 5 icosahedron, icosahedra a ...
polyicosahedron (pI) ,
 , {3,5,5/2}
, {3,5,5/2}, 120
{3,5}
 , 1200
, 1200{3}
{5/2}
{5,5/2}
 , 4
, 480
, - align=center BGCOLOR="#ffe0e0"
,
, 4
, 480
, - align=center BGCOLOR="#ffe0e0"
, Small stellated 120-cell
In geometry, the small stellated 120-cell or stellated polydodecahedron is a regular star 4-polytope with Schläfli symbol . It is one of 10 regular Schläfli-Hess polytopes.
Related polytopes
It has the same edge arrangement as the great gr ...
stellated polydodecahedron (spD) ,
 , {5/2,5,3}
, {5/2,5,3}, 120
{5/2,5}
 , 720
, 720{5/2}
{3}
{5,3}
 , 4
, −480
, - align=center BGCOLOR="#e0ffe0"
,
, 4
, −480
, - align=center BGCOLOR="#e0ffe0"
, Great 120-cell
In geometry, the great 120-cell or great polydodecahedron is a regular star 4-polytope with Schläfli symbol . It is one of 10 regular Schläfli-Hess polytopes. It is one of the two such polytopes that is self-dual.
Related polytopes
It has ...
great polydodecahedron (gpD) ,
 , {5,5/2,5}
, {5,5/2,5}, 120
{5,5/2}
 , 720
, 720{5}
{5}
{5/2,5}
 , 6
, 0
, - align=center BGCOLOR="#e0e0ff"
,
, 6
, 0
, - align=center BGCOLOR="#e0e0ff"
, Grand 120-cell
In geometry, the grand 120-cell or grand polydodecahedron is a regular star 4-polytope with Schläfli symbol . It is one of 10 regular Schläfli-Hess polytopes.
It is one of four ''regular star 4-polytopes'' discovered by Ludwig Schläfli. It is n ...
grand polydodecahedron (apD) ,
 , {5,3,5/2}
, {5,3,5/2}, 120
{5,3}
 , 720
, 720{5}
{5/2}
{3,5/2}
 , 20
, 0
, - align=center BGCOLOR="#ffe0e0"
,
, 20
, 0
, - align=center BGCOLOR="#ffe0e0"
, Great stellated 120-cell
In geometry, the great stellated 120-cell or great stellated polydodecahedron is a regular star 4-polytope with Schläfli symbol . It is one of 10 regular Schläfli-Hess polytopes.
It is one of four ''regular star 4-polytopes'' discovered by Lud ...
great stellated polydodecahedron (gspD) ,
 , {5/2,3,5}
, {5/2,3,5}, 120
{5/2,3}
 , 720
, 720{5/2}
{5}
{3,5}
 , 20
, 0
, - align=center BGCOLOR="#e0ffe0"
,
, 20
, 0
, - align=center BGCOLOR="#e0ffe0"
, Grand stellated 120-cell
In geometry, the grand stellated 120-cell or grand stellated polydodecahedron is a regular star 4-polytope with Schläfli symbol . It is one of 10 regular Schläfli-Hess polytopes.
It is also one of two such polytopes that is self-dual.
Related ...
grand stellated polydodecahedron (aspD) ,
 , {5/2,5,5/2}
, {5/2,5,5/2}, 120
{5/2,5}
 , 720
, 720{5/2}
{5/2}
{5,5/2}
 , 66
, 0
, - align=center BGCOLOR="#e0e0ff"
,
, 66
, 0
, - align=center BGCOLOR="#e0e0ff"
, Great grand 120-cell
In geometry, the great grand 120-cell or great grand polydodecahedron is a regular star 4-polytope with Schläfli symbol . It is one of 10 regular Schläfli-Hess polytopes.
Related polytopes
It has the same edge arrangement as the small stella ...
great grand polydodecahedron (gapD) ,
 , {5,5/2,3}
, {5,5/2,3}, 120
{5,5/2}
 , 720
, 720{5}
{3}
{5/2,3}
 , 76
, −480
, - align=center BGCOLOR="#ffe0e0"
,
, 76
, −480
, - align=center BGCOLOR="#ffe0e0"
, Great icosahedral 120-cell
In geometry, the great icosahedral 120-cell, great polyicosahedron or great faceting, faceted 600-cell is a regular star 4-polytope with Schläfli symbol . It is one of 10 regular Schläfli-Hess polytopes.
Related polytopes
It has the same edge ...
great polyicosahedron (gpI) ,
 , {3,5/2,5}
, {3,5/2,5}, 120
{3,5/2}
 , 1200
, 1200{3}
{5}
{5/2,5}
 , 76
, 480
, - align=center BGCOLOR="#e0e0ff"
,
, 76
, 480
, - align=center BGCOLOR="#e0e0ff"
, Grand 600-cell
In geometry, the grand 600-cell or grand polytetrahedron is a regular star 4-polytope with Schläfli symbol . It is one of 10 regular Schläfli-Hess polytopes. It is the only one with 600 cells.
It is one of four ''regular star 4-polytopes'' disc ...
grand polytetrahedron (apT) ,
 , {3,3,5/2}
, {3,3,5/2}, 600
{3,3}
 , 1200
, 1200{3}
{5/2}
{3,5/2}
 , 191
, 0
, - align=center BGCOLOR="#ffe0e0"
,
, 191
, 0
, - align=center BGCOLOR="#ffe0e0"
, Great grand stellated 120-cell
In geometry, the great grand stellated 120-cell or great grand stellated polydodecahedron is a regular star 4-polytope with Schläfli symbol , one of 10 regular Schläfli-Hess 4-polytopes. It is unique among the 10 for having 600 vertices, and ha ...
great grand stellated polydodecahedron (gaspD) ,
 , {5/2,3,3}
, {5/2,3,3}, 120
{5/2,3}
 , 720
, 720{5/2}
{3}
{3,3}
 , 191
, 0
, 191
, 0
See also
*Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. All its elements or -faces (for all , where is the dimension of the polytope) — cells, f ...
* List of regular polytopes
This article lists the regular polytopes and regular polytope compounds in Euclidean geometry, Euclidean, spherical geometry, spherical and hyperbolic geometry, hyperbolic spaces.
The Schläfli symbol describes every regular tessellation of an ' ...
* Infinite regular 4-polytopes:
** One regular Euclidean honeycomb: {4,3,4}
** Four compact regular hyperbolic honeycombs: {3,5,3}, {4,3,5}, {5,3,4}, {5,3,5}
** Eleven paracompact regular hyperbolic honeycombs: {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5}, and {6,3,6}.
* Abstract regular 4-polytopes:
** 11-cell
In mathematics, the 11-cell (or hendecachoron) is a self-dual abstract regular 4-polytope ( four-dimensional polytope). Its 11 cells are hemi-icosahedral. It has 11 vertices, 55 edges and 55 faces. It has Schläfli symbol , with 3 hemi-icosahedr ...
{3,5,3}
** 57-cell
In mathematics, the 57-cell (pentacontakaiheptachoron) is a self-dual abstract regular 4-polytope ( four-dimensional polytope). Its 57 cells are hemi-dodecahedra. It also has 57 vertices, 171 edges and 171 two-dimensional faces.
The symmetry or ...
{5,3,5}
*Uniform 4-polytope
In geometry, a uniform 4-polytope (or uniform polychoron) is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.
There are 47 non-prismatic convex uniform 4-polytopes. There ...
uniform
A uniform is a variety of clothing worn by members of an organization while participating in that organization's activity. Modern uniforms are most often worn by armed forces and paramilitary organizations such as police, emergency services, se ...
4-polytope families constructed from these 6 regular forms.
*Platonic solid
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all edges c ...
* Kepler-Poinsot polyhedra — regular star polyhedron
In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.
There are two general kinds of star polyhedron:
*Polyhedra which self-intersect in a repetitive way.
*Concave p ...
* Star polygon
In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, certain notable ones can arise through truncation operations ...
— regular star polygons
* 4-polytope
In geometry, a 4-polytope (sometimes also called a polychoron, polycell, or polyhedroid) is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), an ...
* 5-polytope
In geometry, a five-dimensional polytope (or 5-polytope) is a polytope in five-dimensional space, bounded by (4-polytope) facets, pairs of which share a polyhedral cell.
Definition
A 5-polytope is a closed five-dimensional figure with vertices ...
* 6-polytope
In six-dimensional geometry, a six-dimensional polytope or 6-polytope is a polytope, bounded by 5-polytope facets.
Definition
A 6-polytope is a closed six-dimensional figure with vertices, edges, faces, cells (3-faces), 4-faces, and 5-faces. A ...
References
Citations
Bibliography
* * * * * * * ** (Paper 10) * *External links
*Jonathan Bowers, 16 regular 4-polytopes
A collection of stereographic projections of 4-polytopes.
A Catalog of Uniform Polytopes
2 hour film about the fourth dimension (contains stereographic projections of all regular 4-polytopes)
Reguläre Polytope
{{DEFAULTSORT:Regular 4-polytope 4-polytopes