|
Great Dodecahedron
In geometry, the great dodecahedron is a Kepler–Poinsot polyhedron, with Schläfli symbol and Coxeter–Dynkin diagram of . It is one of four nonconvex regular polyhedra. It is composed of 12 pentagonal faces (six pairs of parallel pentagons), intersecting each other making a pentagrammic path, with five pentagons meeting at each vertex. The discovery of the great dodecahedron is sometimes credited to Louis Poinsot in 1810, though there is a drawing of something very similar to a great dodecahedron in the 1568 book '' Perspectiva Corporum Regularium'' by Wenzel Jamnitzer. The great dodecahedron can be constructed analogously to the pentagram, its two-dimensional analogue, via the extension of the -pentagonal polytope faces of the core -polytope (pentagons for the great dodecahedron, and line segments for the pentagram) until the figure again closes. Images Related polyhedra It shares the same edge arrangement as the convex regular icosahedron; the compound with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Dodecahedron
In geometry, the great dodecahedron is a Kepler–Poinsot polyhedron, with Schläfli symbol and Coxeter–Dynkin diagram of . It is one of four nonconvex regular polyhedra. It is composed of 12 pentagonal faces (six pairs of parallel pentagons), intersecting each other making a pentagrammic path, with five pentagons meeting at each vertex. The discovery of the great dodecahedron is sometimes credited to Louis Poinsot in 1810, though there is a drawing of something very similar to a great dodecahedron in the 1568 book '' Perspectiva Corporum Regularium'' by Wenzel Jamnitzer. The great dodecahedron can be constructed analogously to the pentagram, its two-dimensional analogue, via the extension of the -pentagonal polytope faces of the core -polytope (pentagons for the great dodecahedron, and line segments for the pentagram) until the figure again closes. Images Related polyhedra It shares the same edge arrangement as the convex regular icosahedron; the compound with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Tiling
In geometry, a spherical polyhedron or spherical tiling is a tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons. Much of the theory of symmetrical polyhedra is most conveniently derived in this way. The most familiar spherical polyhedron is the soccer ball, thought of as a spherical truncated icosahedron. The next most popular spherical polyhedron is the beach ball, thought of as a hosohedron. Some "improper" polyhedra, such as hosohedra and their duals, dihedra, exist as spherical polyhedra, but their flat-faced analogs are degenerate. The example hexagonal beach ball, is a hosohedron, and is its dual dihedron. History The first known man-made polyhedra are spherical polyhedra carved in stone. Many have been found in Scotland, and appear to date from the neolithic period (the New Stone Age). During the 10th Century, the Islamic scholar Abū al-Wafā' Būzjānī (Abu'l Wafa) wrote the first ser ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dodecahedron
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120. Some dodecahedra have the same combinatorial structure as the regular dodecahedron (in terms of the graph formed by its vertices and edges), but their pentagonal faces are not regular: The pyritohedron, a common crystal form in pyrite, has pyritohedral symmetry, while the tetartoid has tetrahedral symmetry. The rhombic dodecahedron can be seen as a limiting case of the pyritohedron, and it has octahedral symmetry. The elongated dodecahedron and trapezo-rhombic dodecahedron variations, along with the rhombic dodecahedra, are space-filling. There ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Excavated Dodecahedron
In geometry, the excavated dodecahedron is a star polyhedron that looks like a dodecahedron with concave pentagonal pyramids in place of its faces. Its exterior surface represents the Ef1g1 stellation of the icosahedron. It appears in Magnus Wenninger's book ''Polyhedron Models'' as model 28, the ''third stellation of icosahedron''. Description All 20 vertices and 30 of its 60 edges belong to its dodecahedral hull. The 30 other internal edges are longer and belong to a great stellated dodecahedron. (Each contains one of the 30 edges of the icosahedral core.) There are 20 faces corresponding to the 20 vertices. Each face is a self-intersecting hexagon with alternating long and short edges and 60° angles. The equilateral triangles touching a short edge are part of the face. (The smaller one between the long edges is a face of the icosahedral core.) Faceting of the dodecahedron It has the same external form as a certain facetting of the dodecahedron having 20 self-inter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triakis Icosahedron
In geometry, the triakis icosahedron (or kisicosahedronConway, Symmetries of things, p.284) is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated dodecahedron. Cartesian coordinates Let \phi be the golden ratio. The 12 points given by (0, \pm 1, \pm \phi) and cyclic permutations of these coordinates are the vertices of a regular icosahedron. Its dual regular dodecahedron, whose edges intersect those of the icosahedron at right angles, has as vertices the points (\pm 1, \pm 1, \pm 1) together with the points (\pm\phi, \pm 1/\phi, 0) and cyclic permutations of these coordinates. Multiplying all coordinates of this dodecahedron by a factor of (7\phi-1)/11\approx 0.938\,748\,901\,93 gives a slightly smaller dodecahedron. The 20 vertices of this dodecahedron, together with the vertices of the icosahedron, are the vertices of a triakis icosahedron centered at the origin. The length of its long edges equals 2. Its faces are isosceles triangles with one obtuse angl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Complex Icosidodecahedron
In geometry, the small complex icosidodecahedron is a degenerate uniform star polyhedron. Its edges are doubled, making it degenerate. The star has 32 faces (20 triangles and 12 pentagons), 60 (doubled) edges and 12 vertices and 4 sharing faces. The faces in it are considered as two overlapping edges as topological polyhedron. A small complex icosidodecahedron can be constructed from a number of different vertex figures. A very similar figure emerges as a geometrical truncation of the great stellated dodecahedron, where the pentagram faces become doubly-wound pentagons ( --> ), making the internal pentagonal planes, and the three meeting at each vertex become triangles, making the external triangular planes. As a compound The small complex icosidodecahedron can be seen as a compound of the icosahedron and the great dodecahedron where all vertices are precise and edges coincide. The small complex icosidodecahedron resembles an icosahedron, because the great dodecahedron is c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edge Arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes. For example, a ''square vertex arrangement'' is understood to mean four points in a plane, equal distance and angles from a center point. Two polytopes share the same ''vertex arrangement'' if they share the same 0-skeleton. A group of polytopes that shares a vertex arrangement is called an ''army''. Vertex arrangement The same set of vertices can be connected by edges in different ways. For example, the ''pentagon'' and ''pentagram'' have the same ''vertex arrangement'', while the second connects alternate vertices. A ''vertex arrangement'' is often described by the convex hull polytope which contains it. For example, the regular ''pentagram'' can be said to have a (regular) ''pentagonal vertex arrangement''. Infinite tilings can also share common ''vertex arrangements''. For example, this triangular lattice of points ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small Stellated Dodecahedron Truncations
Small may refer to: Science and technology * SMALL, an ALGOL-like programming language * Small (anatomy), the lumbar region of the back * ''Small'' (journal), a nano-science publication * <small>, an HTML element that defines smaller text Arts and entertainment Fictional characters * Small, in the British children's show Big & Small Other uses * Small, of little size * Small (surname) * "Small", a song from the album '' The Cosmos Rocks'' by Queen + Paul Rodgers See also * Smal (other) * List of people known as the Small The Small is an epithet applied to: *Bolko II the Small (c. 1312–1368), Duke of Świdnica, of Jawor and Lwówek, of Lusatia, over half of Brzeg and Oława, of Siewierz, and over half of Głogów and Ścinawa *Dionysius Exiguus (c. 470–c. 5 ... * Smalls (other) {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Wenninger Polyhedron Models
This is an indexed list of the uniform and stellated polyhedra from the book ''Polyhedron Models'', by Magnus Wenninger. The book was written as a guide book to building polyhedra as physical models. It includes templates of face elements for construction and helpful hints in building, and also brief descriptions on the theory behind these shapes. It contains the 75 nonprismatic Uniform polyhedron, uniform polyhedra, as well as 44 Stellation, stellated forms of the convex regular and quasiregular polyhedra. Models listed here can be cited as "Wenninger Model Number ''N''", or ''W''''N'' for brevity. The polyhedra are grouped in 5 tables: Regular (1–5), Semiregular (6–18), regular star polyhedra (20–22,41), Stellations and compounds (19–66), and uniform star polyhedra (67–119). ''The four regular star polyhedra are listed twice because they belong to both the uniform polyhedra and stellation groupings.'' Platonic solids (regular convex polyhedra) W1 to W5 Archimedean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stellation
In geometry, stellation is the process of extending a polygon in two dimensions, polyhedron in three dimensions, or, in general, a polytope in ''n'' dimensions to form a new figure. Starting with an original figure, the process extends specific elements such as its edges or face planes, usually in a symmetrical way, until they meet each other again to form the closed boundary of a new figure. The new figure is a stellation of the original. The word ''stellation'' comes from the Latin ''stellātus'', "starred", which in turn comes from Latin ''stella'', "star". Stellation is the reciprocal or dual process to ''faceting''. Kepler's definition In 1619 Kepler defined stellation for polygons and polyhedra as the process of extending edges or faces until they meet to form a new polygon or polyhedron. He stellated the regular dodecahedron to obtain two regular star polyhedra, the small stellated dodecahedron and great stellated dodecahedron. He also stellated the regular octahedron to o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second Stellation Of Dodecahedron Facets
The second (symbol: s) is the unit of time in the International System of Units (SI), historically defined as of a day – this factor derived from the division of the day first into 24 hours, then to 60 minutes and finally to 60 seconds each (24 × 60 × 60 = 86400). The current and formal definition in the International System of Units ( SI) is more precise:The second ..is defined by taking the fixed numerical value of the caesium frequency, Δ''ν''Cs, the unperturbed ground-state hyperfine transition frequency of the caesium 133 atom, to be when expressed in the unit Hz, which is equal to s−1. This current definition was adopted in 1967 when it became feasible to define the second based on fundamental properties of nature with caesium clocks. Because the speed of Earth's rotation varies and is slowing ever so slightly, a leap second is added at irregular intervals to civil time to keep clocks in sync with Earth's rotation. Uses Analog clocks and watches often ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
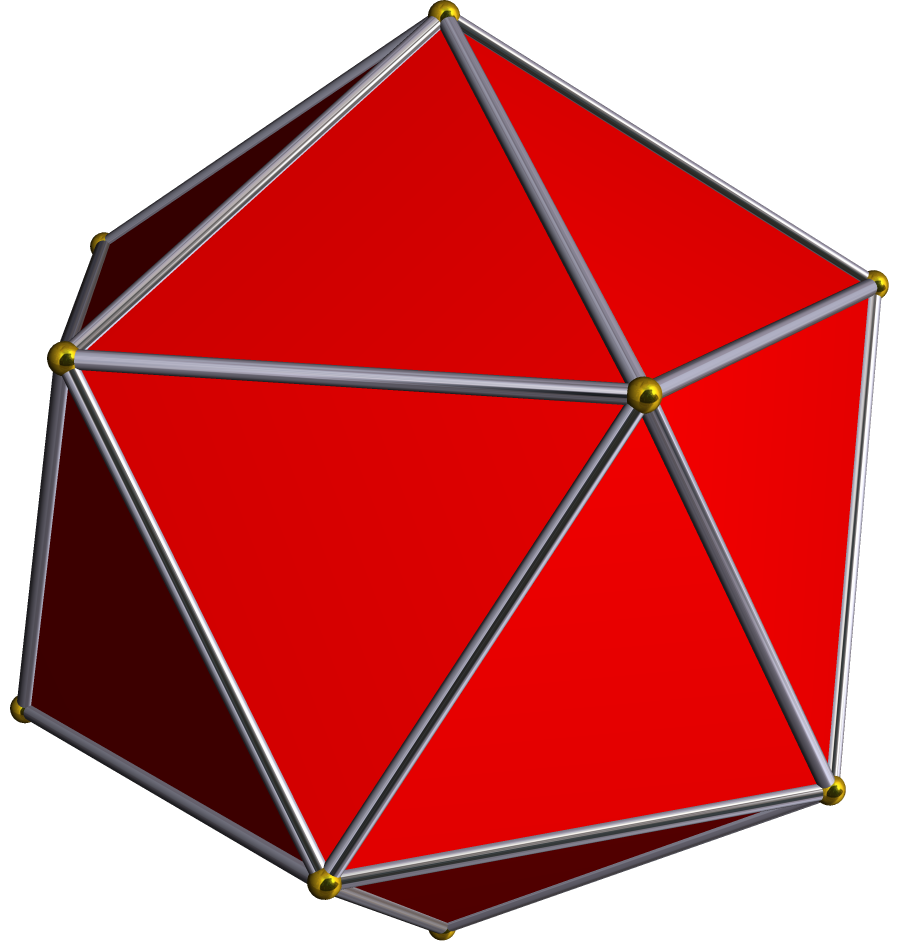
Icosahedron
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes and . The plural can be either "icosahedra" () or "icosahedrons". There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrical than others. The best known is the (convex, non- stellated) regular icosahedron—one of the Platonic solids—whose faces are 20 equilateral triangles. Regular icosahedra There are two objects, one convex and one nonconvex, that can both be called regular icosahedra. Each has 30 edges and 20 equilateral triangle faces with five meeting at each of its twelve vertices. Both have icosahedral symmetry. The term "regular icosahedron" generally refers to the convex variety, while the nonconvex form is called a ''great icosahedron''. Convex regular icosahedron The convex regular icosahedron is usually referred to simply as the ''regular icosahedron'', one of the five regular Platonic solids, and is represented by its Schläfli symbol , con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |