Icosahedron on:
[Wikipedia]
[Google]
[Amazon]

 In
In
 The convex regular icosahedron is usually referred to simply as the ''regular icosahedron'', one of the five regular
The convex regular icosahedron is usually referred to simply as the ''regular icosahedron'', one of the five regular
 The
The
 The coordinates of the 12 vertices can be defined by the vectors defined by all the possible cyclic permutations and sign-flips of coordinates of the form (2, 1, 0). These
The coordinates of the 12 vertices can be defined by the vectors defined by all the possible cyclic permutations and sign-flips of coordinates of the form (2, 1, 0). These
 In Jessen's icosahedron, sometimes called ''Jessen's orthogonal icosahedron'', the 12 isosceles faces are arranged differently so that the figure is non-convex and has
In Jessen's icosahedron, sometimes called ''Jessen's orthogonal icosahedron'', the 12 isosceles faces are arranged differently so that the figure is non-convex and has
 A regular icosahedron is topologically identical to a
A regular icosahedron is topologically identical to a
Icosahedron
on Mathworld.
 In
In geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, an icosahedron ( or ) is a polyhedron
In geometry, a polyhedron (plural polyhedra or polyhedrons; ) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.
A convex polyhedron is the convex hull of finitely many points, not all on ...
with 20 faces. The name comes and . The plural can be either "icosahedra" () or "icosahedrons".
There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrical than others. The best known is the (convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytop ...
, non- stellated) regular icosahedron
In geometry, a regular icosahedron ( or ) is a convex polyhedron with 20 faces, 30 edges and 12 vertices. It is one of the five Platonic solids, and the one with the most faces.
It has five equilateral triangular faces meeting at each vertex. It ...
—one of the Platonic solid
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all e ...
s—whose faces are 20 equilateral triangle
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each oth ...
s.
Regular icosahedra
There are two objects, one convex and one nonconvex, that can both be called regular icosahedra. Each has 30 edges and 20equilateral triangle
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each oth ...
faces with five meeting at each of its twelve vertices. Both have icosahedral symmetry
In mathematics, and especially in geometry, an object has icosahedral symmetry if it has the same symmetries as a regular icosahedron. Examples of other polyhedra with icosahedral symmetry include the regular dodecahedron (the dual of the ...
. The term "regular icosahedron" generally refers to the convex variety, while the nonconvex form is called a ''great icosahedron''.
Convex regular icosahedron
 The convex regular icosahedron is usually referred to simply as the ''regular icosahedron'', one of the five regular
The convex regular icosahedron is usually referred to simply as the ''regular icosahedron'', one of the five regular Platonic solid
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all e ...
s, and is represented by its Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
, containing 20 triangular faces, with 5 faces meeting around each vertex.
Its dual polyhedron
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. ...
is the regular dodecahedron
A regular dodecahedron or pentagonal dodecahedron is a dodecahedron that is regular, which is composed of 12 regular pentagonal faces, three meeting at each vertex. It is one of the five Platonic solids. It has 12 faces, 20 vertices, 30 edges ...
having three regular pentagonal faces around each vertex.
Great icosahedron
 The
The great icosahedron
In geometry, the great icosahedron is one of four Kepler–Poinsot polyhedra (nonconvex regular polyhedra), with Schläfli symbol and Coxeter-Dynkin diagram of . It is composed of 20 intersecting triangular faces, having five triangles meeti ...
is one of the four regular star Kepler-Poinsot polyhedra. Its Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
is . Like the convex form, it also has 20 equilateral triangle faces, but its vertex figure is a pentagram
A pentagram (sometimes known as a pentalpha, pentangle, or star pentagon) is a regular five-pointed star polygon, formed from the diagonal line segments of a convex (or simple, or non-self-intersecting) regular pentagon. Drawing a circle aroun ...
rather than a pentagon, leading to geometrically intersecting faces. The intersections of the triangles do not represent new edges.
Its dual polyhedron
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. ...
is the great stellated dodecahedron
In geometry, the great stellated dodecahedron is a Kepler-Poinsot polyhedron, with Schläfli symbol . It is one of four nonconvex regular polyhedra.
It is composed of 12 intersecting pentagrammic faces, with three pentagrams meeting at each ve ...
, having three regular star pentagonal faces around each vertex.
Stellated icosahedra
Stellation
In geometry, stellation is the process of extending a polygon in two dimensions, polyhedron in three dimensions, or, in general, a polytope in ''n'' dimensions to form a new figure. Starting with an original figure, the process extends specific el ...
is the process of extending the faces or edges of a polyhedron until they meet to form a new polyhedron. It is done symmetrically so that the resulting figure retains the overall symmetry of the parent figure.
In their book ''The Fifty-Nine Icosahedra
''The Fifty-Nine Icosahedra'' is a book written and illustrated by Harold Scott MacDonald Coxeter, H. S. M. Coxeter, Patrick du Val, P. Du Val, H. T. Flather and J. F. Petrie. It enumerates certain stellations of the regular convex or Platonic re ...
'', Coxeter et al. enumerated 58 such stellations of the regular icosahedron.
Of these, many have a single face in each of the 20 face planes and so are also icosahedra. The great icosahedron is among them.
Other stellations have more than one face in each plane or form compounds of simpler polyhedra. These are not strictly icosahedra, although they are often referred to as such.
Pyritohedral symmetry
A ''regular icosahedron'' can be distorted or marked up as a lowerpyritohedral
image:tetrahedron.jpg, 150px, A regular tetrahedron, an example of a solid with full tetrahedral symmetry
A regular tetrahedron has 12 rotational (or orientation-preserving) symmetries, and a symmetry order of 24 including transformations that c ...
symmetry, and is called a snub octahedron, snub tetratetrahedron, snub tetrahedron, and pseudo-icosahedron. This can be seen as an alternated truncated octahedron
In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagon, hexagons and 6 Squa ...
. If all the triangles are equilateral
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each othe ...
, the symmetry can also be distinguished by colouring the 8 and 12 triangle sets differently.
Pyritohedral symmetry
150px, A regular tetrahedron, an example of a solid with full tetrahedral symmetry
A regular tetrahedron has 12 rotational (or orientation-preserving) symmetries, and a symmetry order of 24 including transformations that combine a reflection a ...
has the symbol (3*2), +,4 with order 24. Tetrahedral symmetry
150px, A regular tetrahedron, an example of a solid with full tetrahedral symmetry
A regular tetrahedron has 12 rotational (or orientation-preserving) symmetries, and a symmetry order of 24 including transformations that combine a reflection a ...
has the symbol (332), ,3sup>+, with order 12. These lower symmetries allow geometric distortions from 20 equilateral triangular faces, instead having 8 equilateral triangles and 12 congruent isosceles triangle
In geometry, an isosceles triangle () is a triangle that has two sides of equal length. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at least'' two sides of equal length, the latter versio ...
s.
These symmetries offer Coxeter diagram
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century.
Biography
Coxeter was born in Kensington to ...
s: and respectively, each representing the lower symmetry to the regular icosahedron
In geometry, a regular icosahedron ( or ) is a convex polyhedron with 20 faces, 30 edges and 12 vertices. It is one of the five Platonic solids, and the one with the most faces.
It has five equilateral triangular faces meeting at each vertex. It ...
, (*532), ,3icosahedral symmetry
In mathematics, and especially in geometry, an object has icosahedral symmetry if it has the same symmetries as a regular icosahedron. Examples of other polyhedra with icosahedral symmetry include the regular dodecahedron (the dual of the ...
of order 120.
Cartesian coordinates
 The coordinates of the 12 vertices can be defined by the vectors defined by all the possible cyclic permutations and sign-flips of coordinates of the form (2, 1, 0). These
The coordinates of the 12 vertices can be defined by the vectors defined by all the possible cyclic permutations and sign-flips of coordinates of the form (2, 1, 0). These coordinates
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is sig ...
represent the truncated octahedron
In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagon, hexagons and 6 Squa ...
with alternated vertices deleted.
This construction is called a ''snub tetrahedron'' in its regular icosahedron form, generated by the same operations carried out starting with the vector (''ϕ'', 1, 0), where ''ϕ'' is the golden ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities a and b with a > b > 0,
where the Greek letter phi ( ...
.
Jessen's icosahedron
right
Rights are law, legal, social, or ethics, ethical principles of Liberty, freedom or entitlement; that is, rights are the fundamental normative rules about what is allowed of people or owed to people according to some legal system, social convent ...
dihedral angle
A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the uni ...
s.
It is scissors congruent to a cube, meaning that it can be sliced into smaller polyhedral pieces that can be rearranged to form a solid cube.
Cuboctahedron
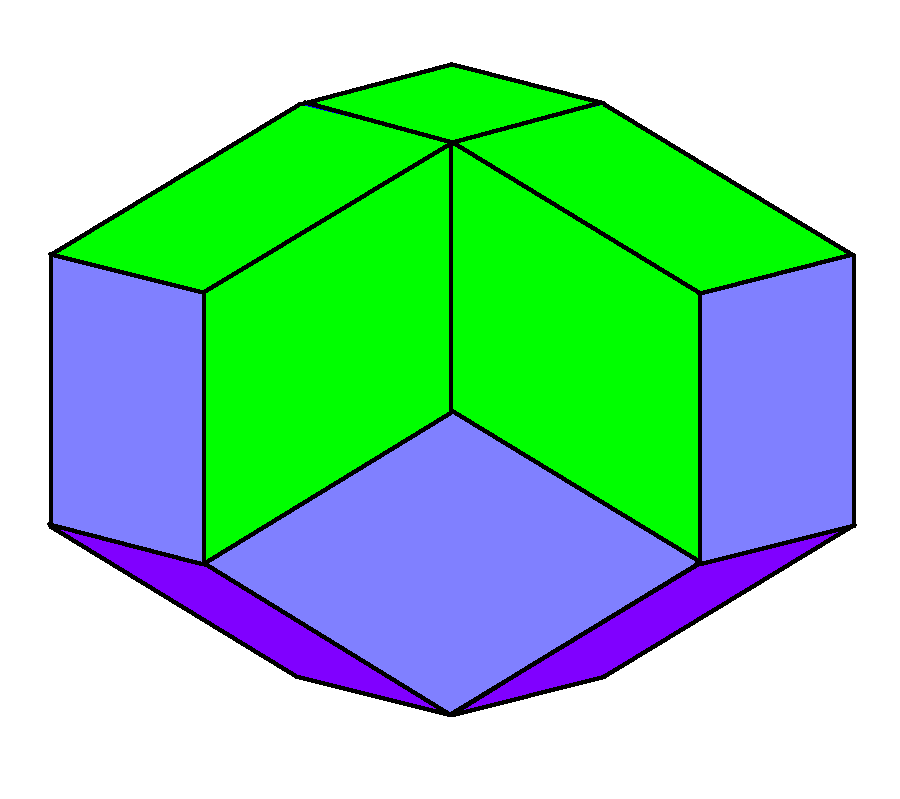
 A regular icosahedron is topologically identical to a
A regular icosahedron is topologically identical to a cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such, it ...
with its 6 square faces bisected on diagonals with pyritohedral symmetry. The icosahedra with pyritohedral symmetry constitute an infinite family of polyhedra which include the cuboctahedron, regular icosahedron, Jessen's icosahedron, and double cover octahedron. Cyclical kinematic transformations among the members of this family exist.
Other icosahedra

Rhombic icosahedron
Therhombic icosahedron
The rhombic icosahedron is a polyhedron shaped like an oblate sphere. Its 20 faces are congruent golden rhombi; 3, 4, or 5 faces meet at each vertex. It has 5 faces (green on top figure) meeting at each of its 2 poles; these 2 vertices lie on it ...
is a zonohedron
In geometry, a zonohedron is a convex polyhedron that is centrally symmetric, every face of which is a polygon that is centrally symmetric (a zonogon). Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in ...
made up of 20 congruent rhombs. It can be derived from the rhombic triacontahedron
In geometry, the rhombic triacontahedron, sometimes simply called the triacontahedron as it is the most common thirty-faced polyhedron, is a convex polyhedron with 30 rhombic faces. It has 60 edges and 32 vertices of two types. It is a Cata ...
by removing 10 middle faces. Even though all the faces are congruent, the rhombic icosahedron is not face-transitive
In geometry, a tessellation of dimension (a plane tiling) or higher, or a polytope of dimension (a polyhedron) or higher, is isohedral or face-transitive if all its faces are the same. More specifically, all faces must be not merely congruent ...
.
Pyramid and prism symmetries
Common icosahedra with pyramid and prism symmetries include: *19-sidedpyramid
A pyramid (from el, πυραμίς ') is a structure whose outer surfaces are triangular and converge to a single step at the top, making the shape roughly a pyramid in the geometric sense. The base of a pyramid can be trilateral, quadrilat ...
(plus 1 base = 20).
*18-sided prism
Prism usually refers to:
* Prism (optics), a transparent optical component with flat surfaces that refract light
* Prism (geometry), a kind of polyhedron
Prism may also refer to:
Science and mathematics
* Prism (geology), a type of sedimentary ...
(plus 2 ends = 20).
*9-sided antiprism
In geometry, an antiprism or is a polyhedron composed of two parallel direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway notation .
Antiprisms are a subclass o ...
(2 sets of 9 sides + 2 ends = 20).
*10-sided bipyramid (2 sets of 10 sides = 20).
*10-sided trapezohedron
In geometry, an trapezohedron, -trapezohedron, -antidipyramid, -antibipyramid, or -deltohedron is the dual polyhedron of an antiprism. The faces of an are congruent and symmetrically staggered; they are called ''twisted kites''. With a hi ...
(2 sets of 10 sides = 20).
Johnson solids
SeveralJohnson solid
In geometry, a Johnson solid is a strictly convex polyhedron each face of which is a regular polygon. There is no requirement that isohedral, each face must be the same polygon, or that the same polygons join around each Vertex (geometry), ver ...
s are icosahedra:on Mathworld.
See also
*600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also known as the C600, hexacosichoron and hexacosihedroid. It is also called a tetraplex (abbreviated from " ...
* Icosoku IcoSoku is a puzzle invented in 2009 by Andrea Mainini and sold by Recent Toys International, which is based in the Netherlands. It won several awards in 2010.
The puzzle frame is a blue plastic icosahedron, and the pieces are 20 white equilat ...
References
{{Authority control Geodesic polyhedra Individual graphs