|
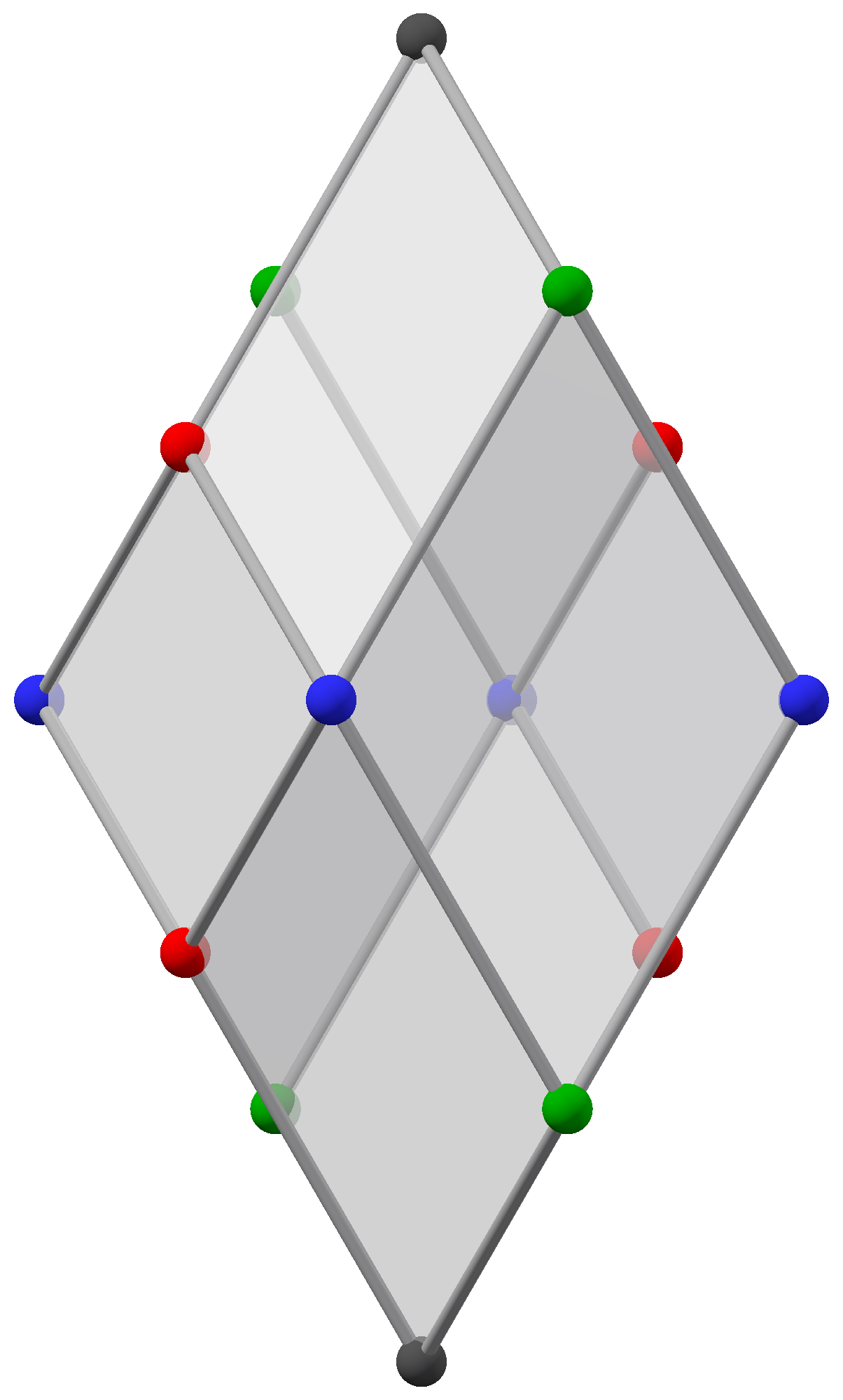
Rhombic Icosahedron
The rhombic icosahedron is a polyhedron shaped like an oblate sphere. Its 20 faces are congruent golden rhombi; 3, 4, or 5 faces meet at each vertex. It has 5 faces (green on top figure) meeting at each of its 2 poles; these 2 vertices lie on its axis of 5-fold symmetry, which is perpendicular to 5 axes of 2-fold symmetry through the midpoints of opposite equatorial edges (example on top figure: most left-hand and most right-hand mid-edges). Its other 10 faces follow its equator, 5 above and 5 below it; each of these 10 rhombi has 2 of its 4 sides lying on this zig-zag skew decagon equator. The rhombic icosahedron has 22 vertices. It has D5d, +,10 (2*5) symmetry group, of order 20; thus it has a center of symmetry (since 5 is odd). Even though all its faces are congruent, the rhombic icosahedron is not face-transitive, since one can distinguish whether a particular face is near the equator or near a pole by examining the types of vertices surrounding this face. Zonohedron T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Icosahedron
The rhombic icosahedron is a polyhedron shaped like an oblate sphere. Its 20 faces are congruent golden rhombi; 3, 4, or 5 faces meet at each vertex. It has 5 faces (green on top figure) meeting at each of its 2 poles; these 2 vertices lie on its axis of 5-fold symmetry, which is perpendicular to 5 axes of 2-fold symmetry through the midpoints of opposite equatorial edges (example on top figure: most left-hand and most right-hand mid-edges). Its other 10 faces follow its equator, 5 above and 5 below it; each of these 10 rhombi has 2 of its 4 sides lying on this zig-zag skew decagon equator. The rhombic icosahedron has 22 vertices. It has D5d, +,10 (2*5) symmetry group, of order 20; thus it has a center of symmetry (since 5 is odd). Even though all its faces are congruent, the rhombic icosahedron is not face-transitive, since one can distinguish whether a particular face is near the equator or near a pole by examining the types of vertices surrounding this face. Zonohedron T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dihedral Symmetry In Three Dimensions
In geometry, dihedral symmetry in three dimensions is one of three infinite sequences of point groups in three dimensions which have a symmetry group that as an abstract group is a dihedral group Dih''n'' (for ''n'' ≥ 2). Types There are 3 types of dihedral symmetry in three dimensions, each shown below in 3 notations: Schönflies notation, Coxeter notation, and orbifold notation. ;Chiral: *''Dn'', 'n'',2sup>+, (22''n'') of order 2''n'' – dihedral symmetry or para-n-gonal group (abstract group: ''Dihn''). ;Achiral: *''Dnh'', 'n'',2 (*22''n'') of order 4''n'' – prismatic symmetry or full ortho-n-gonal group (abstract group: ''Dihn'' × ''Z''2). *''Dnd'' (or ''Dnv''), ''n'',2+ (2*''n'') of order 4''n'' – antiprismatic symmetry or full gyro-n-gonal group (abstract group: ''Dih''2''n''). For a given ''n'', all three have ''n''-fold rotational symmetry about one axis (rotation by an angle of 360°/''n'' does not change the object), and 2-fold rotational symmetr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Dodecahedron T1 H3
Dual or Duals may refer to: Paired/two things * Dual (mathematics), a notion of paired concepts that mirror one another ** Dual (category theory), a formalization of mathematical duality *** see more cases in :Duality theories * Dual (grammatical number), a grammatical category used in some languages * Dual county, a Gaelic games county which in both Gaelic football and hurling * Dual diagnosis, a psychiatric diagnosis of co-occurrence of substance abuse and a mental problem * Dual fertilization, simultaneous application of a P-type and N-type fertilizer * Dual impedance, electrical circuits that are the dual of each other * Dual SIM cellphone supporting use of two SIMs * Aerochute International Dual a two-seat Australian powered parachute design Acronyms and other uses * Dual (brand), a manufacturer of Hifi equipment * DUAL (cognitive architecture), an artificial intelligence design model * DUAL algorithm, or diffusing update algorithm, used to update Internet protocol routing ta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Triacontahedron Middle Colored
Rhombic may refer to: *Rhombus, a quadrilateral whose four sides all have the same length (often called a diamond) *Rhombic antenna, a broadband directional antenna most commonly used on shortwave frequencies * polyhedra formed from rhombuses, such as the rhombic dodecahedron or the rhombic triacontahedron or the rhombic dodecahedral honeycomb or the rhombic icosahedron or the rhombic hexecontahedron or the rhombic enneacontahedron or the trapezo-rhombic dodecahedron * other things that exhibit the shape of a rhombus, such as rhombic tiling, Rhombic Chess, rhombic drive, Rhombic Skaapsteker, rhombic egg eater, rhombic night adder ''Causus rhombeatus'', commonly known as the rhombic night adder, is a viper species endemic to subsaharan Africa. No subspecies are currently recognized. Like all other vipers, it is venomous. Description With an average total length (body + ta ..., forest rhombic night adder {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
6-cube
In geometry, a 6-cube is a six-dimensional hypercube with 64 vertices, 192 edges, 240 square faces, 160 cubic cells, 60 tesseract 4-faces, and 12 5-cube 5-faces. It has Schläfli symbol , being composed of 3 5-cubes around each 4-face. It can be called a hexeract, a portmanteau of tesseract (the ''4-cube'') with ''hex'' for six (dimensions) in Greek. It can also be called a regular dodeca-6-tope or dodecapeton, being a 6-dimensional polytope constructed from 12 regular facets. Related polytopes It is a part of an infinite family of polytopes, called hypercubes. The dual of a 6-cube can be called a 6-orthoplex, and is a part of the infinite family of cross-polytopes. Applying an '' alternation'' operation, deleting alternating vertices of the 6-cube, creates another uniform polytope, called a 6-demicube, (part of an infinite family called demihypercubes), which has 12 5-demicube and 32 5-simplex facets. As a configuration This configuration matrix represents the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Triacontahedron
In geometry, the rhombic triacontahedron, sometimes simply called the triacontahedron as it is the most common thirty-faced polyhedron, is a convex polyhedron with 30 rhombic faces. It has 60 edges and 32 vertices of two types. It is a Catalan solid, and the dual polyhedron of the icosidodecahedron. It is a zonohedron. The ratio of the long diagonal to the short diagonal of each face is exactly equal to the golden ratio, , so that the acute angles on each face measure or approximately 63.43°. A rhombus so obtained is called a ''golden rhombus''. Being the dual of an Archimedean solid, the rhombic triacontahedron is ''face-transitive'', meaning the symmetry group of the solid acts transitively on the set of faces. This means that for any two faces, and , there is a rotation or reflection of the solid that leaves it occupying the same region of space while moving face to face . The rhombic triacontahedron is somewhat special in being one of the nine edge-transitive c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
4-cube
In geometry, a tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells. The tesseract is one of the six convex regular 4-polytopes. The tesseract is also called an 8-cell, C8, (regular) octachoron, octahedroid, cubic prism, and tetracube. It is the four-dimensional hypercube, or 4-cube as a member of the dimensional family of hypercubes or measure polytopes. Coxeter labels it the \gamma_4 polytope. The term ''hypercube'' without a dimension reference is frequently treated as a synonym for this specific polytope. The ''Oxford English Dictionary'' traces the word ''tesseract'' to Charles Howard Hinton's 1888 book ''A New Era of Thought''. The term derives from the Greek ( 'four') and from ( 'ray'), referring to the four edges from each vertex to other vertices. Hinton originally spelled ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bilinski Dodecahedron
In geometry, the Bilinski dodecahedron is a Convex set, convex polyhedron with twelve Congruence (geometry), congruent golden rhombus faces. It has the same topology but a different geometry than the face-transitive rhombic dodecahedron. It is a parallelohedron. History This shape appears in a book by John Lodge Cowley, labeled as the dodecarhombus. It is named after Stanko Bilinski, who rediscovered it in . Bilinski himself called it the rhombic dodecahedron of the second kind.. Bilinski's discovery corrected a -year-old omission in Evgraf Fedorov's classification of convex polyhedra with congruent Rhombus, rhombic faces. Definition and properties Definition The Bilinski dodecahedron is formed by gluing together twelve Congruence (geometry), congruent Golden rhombus, golden rhombi. These are Rhombus, rhombi whose diagonals are in the golden ratio: :\varphi = \approx 1.618~034 . The graph of the resulting polyhedron is Graph isomorphism, isomorphic to the graph of the rhombic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Antiprism
In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces. Hence, it is a non-regular dodecahedron. Geometry If the faces of the pentagonal antiprism are all regular, it is a semiregular polyhedron. It can also be considered as a parabidiminished icosahedron, a shape formed by removing two pentagonal pyramids from a regular icosahedron leaving two nonadjacent pentagonal faces; a related shape, the metabidiminished icosahedron (one of the Johnson solids), is likewise form from the icosahedron by removing two pyramids, but its pentagonal faces are adjacent to each other. The two pentagonal faces of either shape can be augmented with pyramids to form the icosahedron. Relation to polytopes The pentagonal antiprism occurs as a constituent element in some higher-dimensional p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
5-cube
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces. It is represented by Schläfli symbol or , constructed as 3 tesseracts, , around each cubic ridge. It can be called a penteract, a portmanteau of the Greek word , for 'five' (dimensions), and the word ''tesseract'' (the 4-cube). It can also be called a regular deca-5-tope or decateron, being a 5-dimensional polytope constructed from 10 regular facets. Related polytopes It is a part of an infinite hypercube family. The dual of a 5-cube is the 5-orthoplex, of the infinite family of orthoplexes. Applying an '' alternation'' operation, deleting alternating vertices of the 5-cube, creates another uniform 5-polytope, called a 5-demicube, which is also part of an infinite family called the demihypercubes. The 5-cube can be seen as an ''order-3 tesseractic honeycomb'' on a 4-sphere. It is related to the Euclidea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rhombic Icosahedron 5-color-paralleledges
Rhombic may refer to: *Rhombus, a quadrilateral whose four sides all have the same length (often called a diamond) *Rhombic antenna, a broadband directional antenna most commonly used on shortwave frequencies * polyhedra formed from rhombuses, such as the rhombic dodecahedron or the rhombic triacontahedron or the rhombic dodecahedral honeycomb or the rhombic icosahedron or the rhombic hexecontahedron or the rhombic enneacontahedron or the trapezo-rhombic dodecahedron * other things that exhibit the shape of a rhombus, such as rhombic tiling, Rhombic Chess, rhombic drive, Rhombic Skaapsteker, rhombic egg eater, rhombic night adder ''Causus rhombeatus'', commonly known as the rhombic night adder, is a viper species endemic to subsaharan Africa. No subspecies are currently recognized. Like all other vipers, it is venomous. Description With an average total length (body + ta ..., forest rhombic night adder {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallelohedron
In geometry, a parallelohedron is a polyhedron that can be translated without rotations in 3-dimensional Euclidean space to fill space with a honeycomb in which all copies of the polyhedron meet face-to-face. There are five types of parallelohedron, first identified by Evgraf Fedorov in 1885 in his studies of crystallographic systems: the cube, hexagonal prism, rhombic dodecahedron, elongated dodecahedron, and truncated octahedron. Classification Every parallelohedron is a zonohedron, constructed as the Minkowski sum of between three and six line segments. Each of these line segments can have any positive real number as its length, and each edge of a parallelohedron is parallel to one of these generating segments, with the same length. If the length of a segments of a parallelohedron generated from four or more segments is reduced to zero, the result is that the polyhedron degenerates to a simpler form, a parallelohedron formed from one fewer segment. As a zonohedron, these shapes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |