 |
Bilinski Dodecahedron
In geometry, the Bilinski dodecahedron is a convex polyhedron with twelve congruent golden rhombus faces. It has the same topology but a different geometry than the face-transitive rhombic dodecahedron. It is a parallelohedron. History This shape appears in a book by John Lodge Cowley, labeled as the dodecarhombus. It is named after Stanko Bilinski, who rediscovered it in . Bilinski himself called it the rhombic dodecahedron of the second kind.. Bilinski's discovery corrected a -year-old omission in Evgraf Fedorov's classification of convex polyhedra with congruent rhombic faces. Definition and properties Definition The Bilinski dodecahedron is formed by gluing together twelve congruent golden rhombi. These are rhombi whose diagonals are in the golden ratio: :\varphi = \approx 1.618~034 . The graph of the resulting polyhedron is isomorphic to the graph of the rhombic dodecahedron, but the faces are oriented differently: one pair of opposite rhombi has their long an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
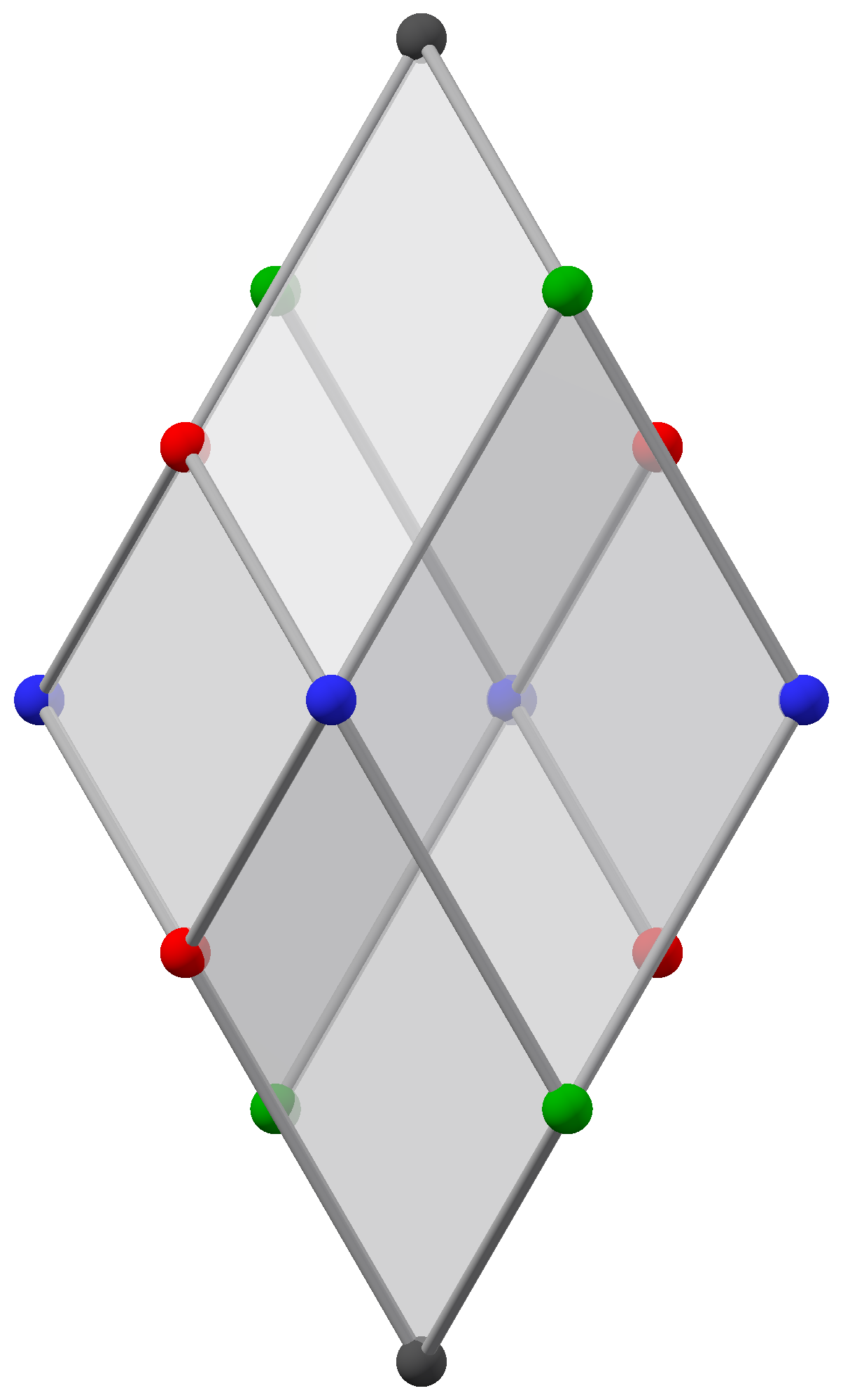
Bilinski Dodecahedron (gray)
In geometry, the Bilinski dodecahedron is a convex polyhedron with twelve congruent golden rhombus faces. It has the same topology but a different geometry than the face-transitive rhombic dodecahedron. It is a parallelohedron. History This shape appears in a 1752 book by John Lodge Cowley, labeled as the dodecarhombus. It is named after Stanko Bilinski, who rediscovered it in 1960. Bilinski himself called it the rhombic dodecahedron of the second kind.. Bilinski's discovery corrected a 75-year-old omission in Evgraf Fedorov's classification of convex polyhedra with congruent rhombic faces. Definition and properties Definition The Bilinski dodecahedron is formed by gluing together twelve congruent golden rhombi. These are rhombi whose diagonals are in the golden ratio: :\varphi = \approx 1.618~034 . The graph of the resulting polyhedron is isomorphic to the graph of the rhombic dodecahedron, but the faces are oriented differently: one pair of opposite rhombi has their ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Rhombic Dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 congruent rhombic faces. It has 24 edges, and 14 vertices of 2 types. It is a Catalan solid, and the dual polyhedron of the cuboctahedron. Properties The rhombic dodecahedron is a zonohedron. Its polyhedral dual is the cuboctahedron. The long face-diagonal length is exactly times the short face-diagonal length; thus, the acute angles on each face measure arccos(), or approximately 70.53°. Being the dual of an Archimedean polyhedron, the rhombic dodecahedron is face-transitive, meaning the symmetry group of the solid acts transitively on its set of faces. In elementary terms, this means that for any two faces A and B, there is a rotation or reflection of the solid that leaves it occupying the same region of space while moving face A to face B. The rhombic dodecahedron can be viewed as the convex hull of the union of the vertices of a cube and an octahedron. The 6 vertices where 4 rhombi meet corres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Golden Rhombus
In geometry, a golden rhombus is a rhombus whose diagonals are in the golden ratio: : = \varphi = \approx 1.618~034 Equivalently, it is the Varignon parallelogram formed from the edge midpoints of a golden rectangle. Rhombi with this shape form the faces of several notable polyhedra. The golden rhombus should be distinguished from the two rhombi of the Penrose tiling, which are both related in other ways to the golden ratio but have different shapes than the golden rhombus. Angles (See the characterizations and the basic properties of the general rhombus for angle properties.) The internal supplementary angles of the golden rhombus are:. See in particular table 1, p. 188. *Acute angle: \alpha=2\arctan ; :by using the arctangent addition formula (see inverse trigonometric functions): :\alpha=\arctan=\arctan=\arctan2\approx63.43495^\circ. : *Obtuse angle: \beta=2\arctan\varphi=\pi-\arctan2\approx116.56505^\circ, :which is also the dihedral angle of the dodecahedron. :Note: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Stanko Bilinski
Stanko Bilinski (22 April 1909 in Našice – 6 April 1998 in Zagreb) was a Croatian mathematician and academician. He was a professor at the University of Zagreb and a fellow of the Croatian Academy of Sciences and Arts. In 1960, he discovered a rhombic dodecahedron of the second kind, the Bilinski dodecahedron. Like the standard rhombic dodecahedron, this convex polyhedron has 12 congruent rhombus In plane Euclidean geometry, a rhombus (plural rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. Th ... sides, but they are differently shaped and arranged. Bilinski's discovery corrected a 75-year-old omission in Evgraf Fedorov's classification of convex polyhedra with congruent rhombic faces.. References Further reading * * 1909 births 1998 deaths Croatian mathematicians Academic staff of the University of Zagreb Members o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Dihedral Symmetry In Three Dimensions
In geometry, dihedral symmetry in three dimensions is one of three infinite sequences of point groups in three dimensions which have a symmetry group that as an abstract group is a dihedral group Dih''n'' (for ''n'' ≥ 2). Types There are 3 types of dihedral symmetry in three dimensions, each shown below in 3 notations: Schönflies notation, Coxeter notation, and orbifold notation. ;Chiral: *''Dn'', 'n'',2sup>+, (22''n'') of order 2''n'' – dihedral symmetry or para-n-gonal group (abstract group: ''Dihn''). ;Achiral: *''Dnh'', 'n'',2 (*22''n'') of order 4''n'' – prismatic symmetry or full ortho-n-gonal group (abstract group: ''Dihn'' × ''Z''2). *''Dnd'' (or ''Dnv''), ''n'',2+ (2*''n'') of order 4''n'' – antiprismatic symmetry or full gyro-n-gonal group (abstract group: ''Dih''2''n''). For a given ''n'', all three have ''n''-fold rotational symmetry about one axis (rotation by an angle of 360°/''n'' does not change the object), and 2-fold rotational symme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Rectangular Cuboid
In geometry, a cuboid is a hexahedron, a six-faced solid. Its faces are quadrilaterals. Cuboid means "like a cube", in the sense that by adjusting the length of the edges or the angles between edges and faces a cuboid can be transformed into a cube. In mathematical language a cuboid is a convex polyhedron, whose polyhedral graph is the same as that of a cube. Special cases are a cube, with 6 squares as faces, a rectangular prism, rectangular cuboid or rectangular box, with 6 rectangles as faces, for both, cube and rectangular prism, adjacent faces meet in a right angle. General cuboids By Euler's formula the numbers of faces ''F'', of vertices ''V'', and of edges ''E'' of any convex polyhedron are related by the formula ''F'' + ''V'' = ''E'' + 2. In the case of a cuboid this gives 6 + 8 = 12 + 2; that is, like a cube, a cuboid has 6 faces, 8 vertices, and 12 edges. Along with the rectangular cuboids, any parallelepip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Graph Isomorphism
In graph theory, an isomorphism of graphs ''G'' and ''H'' is a bijection between the vertex sets of ''G'' and ''H'' : f \colon V(G) \to V(H) such that any two vertices ''u'' and ''v'' of ''G'' are adjacent in ''G'' if and only if f(u) and f(v) are adjacent in ''H''. This kind of bijection is commonly described as "edge-preserving bijection", in accordance with the general notion of isomorphism being a structure-preserving bijection. If an isomorphism exists between two graphs, then the graphs are called isomorphic and denoted as G\simeq H. In the case when the bijection is a mapping of a graph onto itself, i.e., when ''G'' and ''H'' are one and the same graph, the bijection is called an automorphism of ''G''. If a graph is finite, we can prove it to be bijective by showing it is one-one/onto; no need to show both. Graph isomorphism is an equivalence relation on graphs and as such it partitions the class of all graphs into equivalence classes. A set of graphs isomorphic to eac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Golden Ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities a and b with a > b > 0, where the Greek letter phi ( or \phi) denotes the golden ratio. The constant \varphi satisfies the quadratic equation \varphi^2 = \varphi + 1 and is an irrational number with a value of The golden ratio was called the extreme and mean ratio by Euclid, and the divine proportion by Luca Pacioli, and also goes by several other names. Mathematicians have studied the golden ratio's properties since antiquity. It is the ratio of a regular pentagon's diagonal to its side and thus appears in the construction of the dodecahedron and icosahedron. A golden rectangle—that is, a rectangle with an aspect ratio of \varphi—may be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has been used to analyze the proportions of natural o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Rhombus
In plane Euclidean geometry, a rhombus (plural rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the diamonds suit in playing cards which resembles the projection of an octahedral diamond, or a lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle (which some authors call a calisson after the French sweet – also see Polyiamond), and the latter sometimes refers specifically to a rhombus with a 45° angle. Every rhombus is simple (non-self-intersecting), and is a special case of a parallelogram and a kite. A rhombus with right angles is a square. Etymology The word "rhombus" comes from grc, ῥόμβος, rhombos, meaning something that spins, which derives from the verb , romanized: , meaning "to turn round and round." The word was used both by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Evgraf Fedorov
Evgraf Stepanovich Fedorov (russian: Евгра́ф Степа́нович Фёдоров, – 21 May 1919) was a Russian mathematician, crystallographer and mineralogist. Fedorov was born in the Russian city of Orenburg. His father was a topographical engineer. The family later moved to Saint Petersburg. From the age of fifteen, he was deeply interested in the theory of polytopes, which later became his main research interest. He was a distinguished graduate of the Gorny Institute, which he joined at the age of 26. He was elected the first Director of the Institute in 1905. He contributed to the identification of conditions under which a group of Euclidean motions must have a translational subgroup whose vectors span the Euclidean space. He undertook investigations into crystal structure as early as 1881. His best-known result is his 1891 derivation of the 230 symmetry space groups which now serve as the mathematical basis of structural analysis. He also proved that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Cambridge University Press
Cambridge University Press is the university press of the University of Cambridge. Granted letters patent by Henry VIII of England, King Henry VIII in 1534, it is the oldest university press in the world. It is also the King's Printer. Cambridge University Press is a department of the University of Cambridge and is both an academic and educational publisher. It became part of Cambridge University Press & Assessment, following a merger with Cambridge Assessment in 2021. With a global sales presence, publishing hubs, and offices in more than 40 Country, countries, it publishes over 50,000 titles by authors from over 100 countries. Its publishing includes more than 380 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also publishes Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Spo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |