|
11-cell
In mathematics, the 11-cell is a self-dual abstract regular 4-polytope ( four-dimensional polytope). Its 11 cells are hemi-icosahedral. It has 11 vertices, 55 edges and 55 faces. It has Schläfli type , with 3 hemi-icosahedra (Schläfli type ) around each edge. It has symmetry order 660, computed as the product of the number of cells (11) and the symmetry of each cell (60). The symmetry structure is the abstract group projective special linear group of the 2-dimensional vector space over the finite field with 11 elements L2(11). It was discovered in 1976 by Branko Grünbaum Branko Grünbaum (; 2 October 1929 – 14 September 2018) was a Croatian-born mathematician of Jewish descent [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abstract Polytope
In mathematics, an abstract polytope is an algebraic partially ordered set which captures the dyadic property of a traditional polytope without specifying purely geometric properties such as points and lines. A geometric polytope is said to be a ''realization'' of an abstract polytope in some real N-dimensional space, typically Euclidean space, Euclidean. This abstract definition allows more general combinatorics, combinatorial structures than traditional definitions of a polytope, thus allowing new objects that have no counterpart in traditional theory. Introductory concepts Traditional versus abstract polytopes In Euclidean geometry, two shapes that are not Similar (geometry), similar can nonetheless share a common structure. For example, a square and a trapezoid both comprise an alternating chain of four vertex (geometry), vertices and four sides, which makes them quadrilaterals. They are said to be isomorphic or “structure preserving”. This common structure may ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
57-cell
In mathematics, the 57-cell (pentacontaheptachoron) is a self-dual abstract regular 4-polytope ( four-dimensional polytope). Its 57 cells are hemi-dodecahedra. It also has 57 vertices, 171 edges and 171 two-dimensional faces. The symmetry order is 3420, from the product of the number of cells (57) and the symmetry of each cell (60). The symmetry abstract structure is the projective special linear group of the 2-dimensional vector space over the finite field of 19 elements, L2(19). It has Schläfli type with 5 hemi-dodecahedral cells around each edge. It was discovered by . Perkel graph The vertices and edges form the Perkel graph, the unique distance-regular graph with intersection array , discovered by . See also * 11-cell – abstract regular polytope with hemi-icosahedral cells. * 120-cell In geometry, the 120-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called a C120, dodecaplex ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
4-polytope
In geometry, a 4-polytope (sometimes also called a polychoron, polycell, or polyhedroid) is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: Vertex (geometry), vertices, Edge (geometry), edges, Face (geometry), faces (polygons), and Cell (mathematics), cells (Polyhedron, polyhedra). Each face is shared by exactly two cells. The 4-polytopes were discovered by the Swiss mathematician Ludwig Schläfli before 1853. The two-dimensional analogue of a 4-polytope is a polygon, and the three-dimensional analogue is a polyhedron. Topologically 4-polytopes are closely related to the Convex uniform honeycomb, uniform honeycombs, such as the cubic honeycomb, which tessellate 3-space; similarly the 3D cube is related to the infinite 2D square tiling. Convex 4-polytopes can be ''cut and unfolded'' as polyhedral net, nets in 3-space. Definition A 4-polytope is a closed Four-dimensional space, four-dimensional figure. It compr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
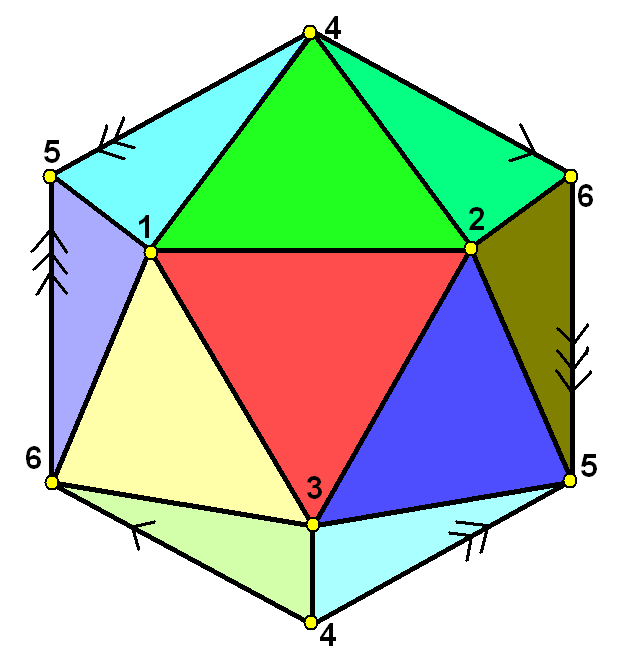
Hemi-icosahedron Coloured
In geometry, a hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 10 triangles), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts. Geometry It has 10 triangular faces, 15 edges, and 6 vertices. It is also related to the nonconvex uniform polyhedron, the tetrahemihexahedron, which could be topologically identical to the hemi-icosahedron if each of the 3 square faces were divided into two triangles. Graphs It can be represented symmetrically on faces, and vertices as Schlegel diagrams: The complete graph K6 It has the same vertices and edges as the 5-dimensional 5-simplex which has a complete graph of edges, but only contains half of the (20) faces. From the point of view of graph theory this is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hemi-icosahedron
In geometry, a hemi-icosahedron is an abstract polytope, abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 10 triangles), which can be visualized by constructing the projective plane as a wikt:hemisphere, hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts. Geometry It has 10 triangular faces, 15 edges, and 6 vertices. It is also related to the nonconvex uniform polyhedron, the tetrahemihexahedron, which could be topologically identical to the hemi-icosahedron if each of the 3 square faces were divided into two triangles. Graphs It can be represented symmetrically on faces, and vertices as Schlegel diagrams: The complete graph K6 It has the same vertices and edges as the 5-dimensional 5-simplex which has a complete graph of edges, but only contains half of the (20) faces. From the po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Icosahedral Honeycomb
In geometry, the icosahedral honeycomb is one of four compact, List of regular polytopes and compounds, regular, space-filling tessellations (or honeycomb (geometry), honeycombs) in Hyperbolic space, hyperbolic 3-space. With Schläfli symbol there are three regular icosahedron, icosahedra around each Edge (geometry), edge, and 12 icosahedra around each Vertex (geometry), vertex, in a regular regular dodecahedron, dodecahedral vertex figure. It is analogous to the 24-cell and the 5-cell. Description The dihedral angle of a regular icosahedron is around 138.2°, so it is impossible to fit three icosahedra around an edge in Euclidean 3-space. However, in hyperbolic space, properly scaled icosahedra can have dihedral angles of exactly 120 degrees, so three of those can fit around an edge. Related regular honeycombs There are four regular compact honeycombs in 3D hyperbolic space: Related regular polytopes and honeycombs It is a member of a sequence of regular polychora and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
5-simplex
In five-dimensional geometry, a 5-simplex is a self-dual regular 5-polytope. It has six vertices, 15 edges, 20 triangle faces, 15 tetrahedral cells, and 6 5-cell facets. It has a dihedral angle of cos−1(), or approximately 78.46°. The 5-simplex is a solution to the problem: ''Make 20 equilateral triangles using 15 matchsticks, where each side of every triangle is exactly one matchstick.'' Alternate names It can also be called a hexateron, or hexa-5-tope, as a 6- facetted polytope in 5-dimensions. The name ''hexateron'' is derived from ''hexa-'' for having six facets and '' teron'' (with ''ter-'' being a corruption of ''tetra-'') for having four-dimensional facets. By Jonathan Bowers, a hexateron is given the acronym hix. As a configuration This configuration matrix represents the 5-simplex. The rows and columns correspond to vertices, edges, faces, cells and 4-faces. The diagonal numbers say how many of each element occur in the whole 5-simplex. The nondiagonal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
10-simplex
In geometry, a 10-simplex is a self-dual regular 10-polytope. It has 11 vertices, 55 edges, 165 triangle faces, 330 tetrahedral cells, 462 5-cell 4-faces, 462 5-simplex 5-faces, 330 6-simplex 6-faces, 165 7-simplex 7-faces, 55 8-simplex 8-faces, and 11 9-simplex 9-faces. Its dihedral angle is cos−1(1/10), or approximately 84.26°. It can also be called a hendecaxennon, or hendeca-10-tope, as an 11- facetted polytope in 10-dimensions. Acronym: ux The name ''hendecaxennon'' is derived from ''hendeca'' for 11 facets in Greek and -xenn (variation of ennea for nine), having 9-dimensional facets, and ''-on''. Coordinates The Cartesian coordinate In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...s of the vertices of an origin-centered regular 10-simplex having edge length ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Subspace
In geometry, a flat is an affine subspace, i.e. a subset of an affine space that is itself an affine space. Particularly, in the case the parent space is Euclidean, a flat is a Euclidean subspace which inherits the notion of distance from its parent space. In an -dimensional space, there are -flats of every dimension from 0 to ; flats one dimension lower than the parent space, -flats, are called ''hyperplanes''. The flats in a plane (two-dimensional space) are points, lines, and the plane itself; the flats in three-dimensional space are points, lines, planes, and the space itself. The definition of flat excludes non-straight curves and non-planar surfaces, which are subspaces having different notions of distance: arc length and geodesic length, respectively. Flats occur in linear algebra, as geometric realizations of solution sets of systems of linear equations. A flat is a manifold and an algebraic variety, and is sometimes called a ''linear manifold'' or ''linear va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
10-simplex T0
1 (one, unit, unity) is a number, numeral, and glyph. It is the first and smallest positive integer of the infinite sequence of natural numbers. This fundamental property has led to its unique uses in other fields, ranging from science to sports, where it commonly denotes the first, leading, or top thing in a group. 1 is the unit of counting or measurement, a determiner for singular nouns, and a gender-neutral pronoun. Historically, the representation of 1 evolved from ancient Sumerian and Babylonian symbols to the modern Arabic numeral. In mathematics, 1 is the multiplicative identity, meaning that any number multiplied by 1 equals the same number. 1 is by convention not considered a prime number. In digital technology, 1 represents the "on" state in binary code, the foundation of computing. Philosophically, 1 symbolizes the ultimate reality or source of existence in various traditions. In mathematics The number 1 is the first natural number after 0. Each natural number, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |