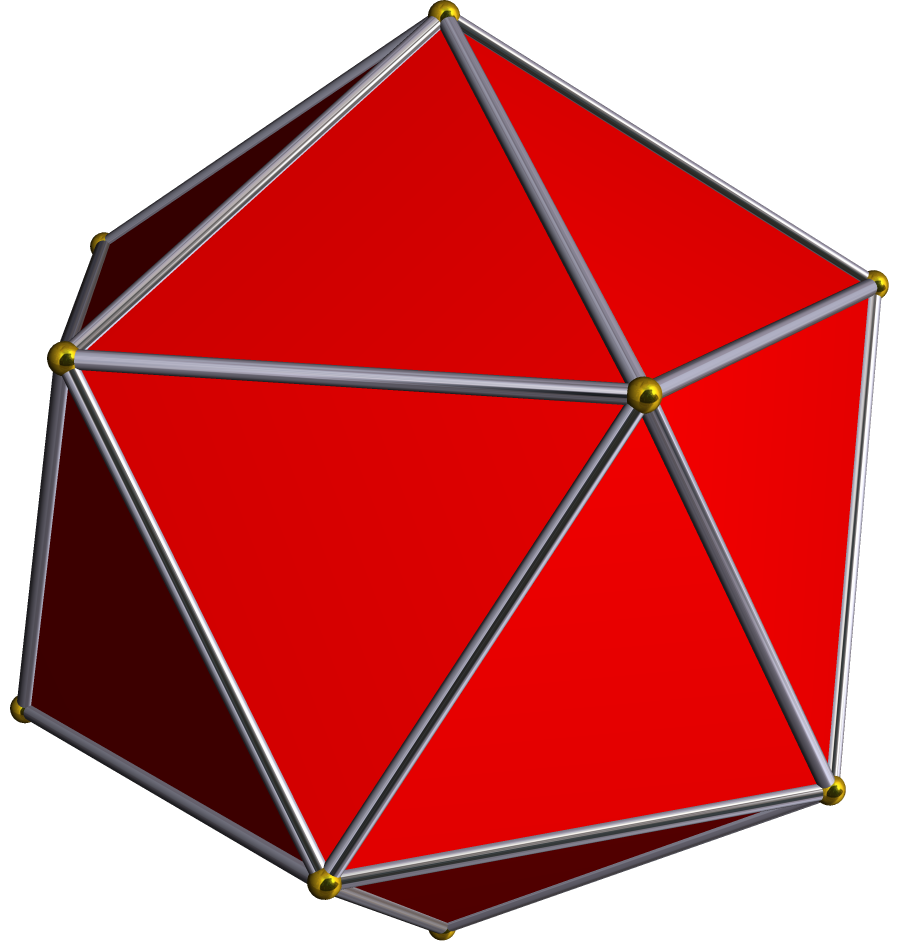
|
Great Stellated Dodecahedron
In geometry, the great stellated dodecahedron is a Kepler-Poinsot polyhedron, with Schläfli symbol . It is one of four nonconvex regular polyhedra. It is composed of 12 intersecting pentagrammic faces, with three pentagrams meeting at each vertex. It shares its vertex arrangement, although not its vertex figure or vertex configuration, with the regular dodecahedron, as well as being a stellation of a (smaller) dodecahedron. It is the only dodecahedral stellation with this property, apart from the dodecahedron itself. Its dual, the great icosahedron, is related in a similar fashion to the icosahedron. Shaving the triangular pyramids off results in an icosahedron. If the pentagrammic faces are broken into triangles, it is topologically related to the triakis icosahedron, with the same face connectivity, but much taller isosceles triangle faces. If the triangles are instead made to invert themselves and excavate the central icosahedron, the result is a great dodecahedron. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Stellated Dodecahedron
In geometry, the great stellated dodecahedron is a Kepler-Poinsot polyhedron, with Schläfli symbol . It is one of four nonconvex regular polyhedra. It is composed of 12 intersecting pentagrammic faces, with three pentagrams meeting at each vertex. It shares its vertex arrangement, although not its vertex figure or vertex configuration, with the regular dodecahedron, as well as being a stellation of a (smaller) dodecahedron. It is the only dodecahedral stellation with this property, apart from the dodecahedron itself. Its dual, the great icosahedron, is related in a similar fashion to the icosahedron. Shaving the triangular pyramids off results in an icosahedron. If the pentagrammic faces are broken into triangles, it is topologically related to the triakis icosahedron, with the same face connectivity, but much taller isosceles triangle faces. If the triangles are instead made to invert themselves and excavate the central icosahedron, the result is a great dodecahedron. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Polytope
In geometry, a pentagonal polytope is a regular polytope in ''n'' dimensions constructed from the H''n'' Coxeter group. The family was named by H. S. M. Coxeter, because the two-dimensional pentagonal polytope is a pentagon. It can be named by its Schläfli symbol as (dodecahedral) or (icosahedral). Family members The family starts as 1-polytopes and ends with ''n'' = 5 as infinite tessellations of 4-dimensional hyperbolic space. There are two types of pentagonal polytopes; they may be termed the ''dodecahedral'' and ''icosahedral'' types, by their three-dimensional members. The two types are duals of each other. Dodecahedral The complete family of dodecahedral pentagonal polytopes are: # Line segment, # Pentagon, # Dodecahedron, (12 pentagonal faces) # 120-cell, (120 dodecahedral cells) # Order-3 120-cell honeycomb, (tessellates hyperbolic 4-space (∞ 120-cell facets) The facets of each dodecahedral pentagonal polytope are the dodecahedral pentagonal polytopes o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncated Great Stellated Dodecahedron
In geometry, the small complex icosidodecahedron is a degenerate uniform star polyhedron. Its edges are doubled, making it degenerate. The star has 32 faces (20 triangles and 12 pentagons), 60 (doubled) edges and 12 vertices and 4 sharing faces. The faces in it are considered as two overlapping edges as topological polyhedron. A small complex icosidodecahedron can be constructed from a number of different vertex figures. A very similar figure emerges as a geometrical truncation of the great stellated dodecahedron, where the pentagram faces become doubly-wound pentagons ( --> ), making the internal pentagonal planes, and the three meeting at each vertex become triangles, making the external triangular planes. As a compound The small complex icosidodecahedron can be seen as a compound of the icosahedron and the great dodecahedron where all vertices are precise and edges coincide. The small complex icosidodecahedron resembles an icosahedron, because the great dodecahedron is c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex. The term originates from Kepler's names for the Archimedean solids. Uniform truncation In general any polyhedron (or polytope) can also be truncated with a degree of freedom as to how deep the cut is, as shown in Conway polyhedron notation truncation operation. A special kind of truncation, usually implied, is a uniform truncation, a truncation operator applied to a regular polyhedron (or regular polytope) which creates a resulting uniform polyhedron (uniform polytope) with equal edge lengths. There are no degrees of freedom, and it represents a fixed geometric, just like the regular polyhedra. In general all single ringed uniform polytopes have a uniform truncation. For example, the icosidodecahedron, represented as Schläfli symbols r or \begin 5 \\ 3 \end, and Coxeter-Dynkin diagram or has a uniform truncation, the truncated icosidodeca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Icosidodecahedron
In geometry, the great icosidodecahedron is a nonconvex uniform polyhedron, indexed as U54. It has 32 faces (20 triangles and 12 pentagrams), 60 edges, and 30 vertices. It is given a Schläfli symbol r. It is the rectification of the great stellated dodecahedron and the great icosahedron. It was discovered independently by , and . Related polyhedra The name is constructed analogously as how a cube-octahedron creates a cuboctahedron, and how a dodecahedron-icosahedron creates a (small) icosidodecahedron. It shares the same vertex arrangement with the icosidodecahedron, its convex hull. Unlike the great icosahedron and great dodecahedron, the great icosidodecahedron is not a stellation of the icosidodecahedron, but a faceting of it instead. It also shares its edge arrangement with the great icosihemidodecahedron (having the triangular faces in common), and with the great dodecahemidodecahedron (having the pentagrammic faces in common). This polyhedron can be considered a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Stellated Dodecahedron Truncations
Great may refer to: Descriptions or measurements * Great, a relative measurement in physical space, see Size * Greatness, being divine, majestic, superior, majestic, or transcendent People * List of people known as "the Great" *Artel Great (born 1981), American actor Other uses * ''Great'' (1975 film), a British animated short about Isambard Kingdom Brunel * ''Great'' (2013 film), a German short film * Great (supermarket), a supermarket in Hong Kong * GReAT, Graph Rewriting and Transformation, a Model Transformation Language * Gang Resistance Education and Training Gang Resistance Education And Training, abbreviated G.R.E.A.T., provides a school-based, police officer instructed program that includes classroom instruction and various learning activities. Their intention is to teach the students to avoid gan ..., or GREAT, a school-based and police officer-instructed program * Global Research and Analysis Team (GReAT), a cybersecurity team at Kaspersky Lab *'' Great!'', a 20 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Net Of A Great Stellated Dodecahedron
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Wenninger Polyhedron Models
This is an indexed list of the uniform and stellated polyhedra from the book ''Polyhedron Models'', by Magnus Wenninger. The book was written as a guide book to building polyhedra as physical models. It includes templates of face elements for construction and helpful hints in building, and also brief descriptions on the theory behind these shapes. It contains the 75 nonprismatic Uniform polyhedron, uniform polyhedra, as well as 44 Stellation, stellated forms of the convex regular and quasiregular polyhedra. Models listed here can be cited as "Wenninger Model Number ''N''", or ''W''''N'' for brevity. The polyhedra are grouped in 5 tables: Regular (1–5), Semiregular (6–18), regular star polyhedra (20–22,41), Stellations and compounds (19–66), and uniform star polyhedra (67–119). ''The four regular star polyhedra are listed twice because they belong to both the uniform polyhedra and stellation groupings.'' Platonic solids (regular convex polyhedra) W1 to W5 Archimedean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Third Stellation Of Dodecahedron Facets
Third or 3rd may refer to: Numbers * 3rd, the ordinal form of the cardinal number 3 * , a fraction of one third * 1⁄60 of a ''second'', or 1⁄3600 of a ''minute'' Places * 3rd Street (other) * Third Avenue (other) * Highway 3 Music Music theory * Interval number of three in a musical interval **major third, a third spanning four semitones **minor third, a third encompassing three half steps, or semitones ** neutral third, wider than a minor third but narrower than a major third **augmented third, an interval of five semitones **diminished third, produced by narrowing a minor third by a chromatic semitone * Third (chord), chord member a third above the root *Degree (music), three away from tonic **mediant, third degree of the diatonic scale **submediant, sixth degree of the diatonic scale – three steps below the tonic ** chromatic mediant, chromatic relationship by thirds *Ladder of thirds, similar to the circle of fifths Albums *''Third/Sister Lovers' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Great Stellated Dodecahedron Net
Great may refer to: Descriptions or measurements * Great, a relative measurement in physical space, see Size * Greatness, being divine, majestic, superior, majestic, or transcendent People * List of people known as "the Great" *Artel Great (born 1981), American actor Other uses * ''Great'' (1975 film), a British animated short about Isambard Kingdom Brunel * ''Great'' (2013 film), a German short film * Great (supermarket), a supermarket in Hong Kong * GReAT, Graph Rewriting and Transformation, a Model Transformation Language * Gang Resistance Education and Training Gang Resistance Education And Training, abbreviated G.R.E.A.T., provides a school-based, police officer instructed program that includes classroom instruction and various learning activities. Their intention is to teach the students to avoid gan ..., or GREAT, a school-based and police officer-instructed program * Global Research and Analysis Team (GReAT), a cybersecurity team at Kaspersky Lab *'' Great!'', a 20 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Net (polyhedron)
In geometry, a net of a polyhedron is an arrangement of non-overlapping edge-joined polygons in the plane which can be folded (along edges) to become the faces of the polyhedron. Polyhedral nets are a useful aid to the study of polyhedra and solid geometry in general, as they allow for physical models of polyhedra to be constructed from material such as thin cardboard. An early instance of polyhedral nets appears in the works of Albrecht Dürer, whose 1525 book ''A Course in the Art of Measurement with Compass and Ruler'' (''Unterweysung der Messung mit dem Zyrkel und Rychtscheyd '') included nets for the Platonic solids and several of the Archimedean solids. These constructions were first called nets in 1543 by Augustin Hirschvogel. Existence and uniqueness Many different nets can exist for a given polyhedron, depending on the choices of which edges are joined and which are separated. The edges that are cut from a convex polyhedron to form a net must form a spanning tree of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Tiling
In geometry, a spherical polyhedron or spherical tiling is a tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons. Much of the theory of symmetrical polyhedra is most conveniently derived in this way. The most familiar spherical polyhedron is the soccer ball, thought of as a spherical truncated icosahedron. The next most popular spherical polyhedron is the beach ball, thought of as a hosohedron. Some "improper" polyhedra, such as hosohedra and their duals, dihedra, exist as spherical polyhedra, but their flat-faced analogs are degenerate. The example hexagonal beach ball, is a hosohedron, and is its dual dihedron. History The first known man-made polyhedra are spherical polyhedra carved in stone. Many have been found in Scotland, and appear to date from the neolithic period (the New Stone Age). During the 10th Century, the Islamic scholar Abū al-Wafā' Būzjānī (Abu'l Wafa) wrote the first s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
