Resonant Frequency Amplitude on:
[Wikipedia]
[Google]
[Amazon]
 Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic
 A familiar example is a playground
A familiar example is a playground
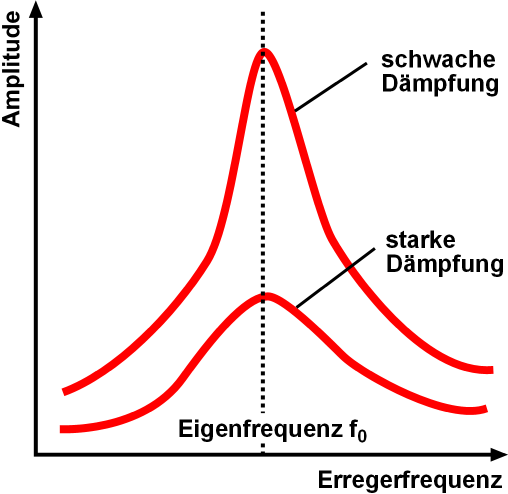
 Resonance occurs when, at certain driving frequencies, the steady-state amplitude of ''x''(''t'') is large compared to its amplitude at other driving frequencies. For the mass on a spring, resonance corresponds physically to the mass's oscillations having large displacements from the spring's equilibrium position at certain driving frequencies. Looking at the amplitude of ''x''(''t'') as a function of the driving frequency ''ω'', the amplitude is maximal at the driving frequency
''ω''''r'' is the resonant frequency for this system. Again, note that the resonant frequency does not equal the undamped angular frequency ''ω''0 of the oscillator. They are proportional, and if the damping ratio goes to zero they are the same, but for non-zero damping they are not the same frequency. As shown in the figure, resonance may also occur at other frequencies near the resonant frequency, including ''ω''0, but the maximum response is at the resonant frequency.
Also note that ''ω''''r'' is only real and non-zero if , so this system can only resonate when the harmonic oscillator is significantly underdamped. For systems with a very small damping ratio and a driving frequency near the resonant frequency, the steady state oscillations can become very large.
Resonance occurs when, at certain driving frequencies, the steady-state amplitude of ''x''(''t'') is large compared to its amplitude at other driving frequencies. For the mass on a spring, resonance corresponds physically to the mass's oscillations having large displacements from the spring's equilibrium position at certain driving frequencies. Looking at the amplitude of ''x''(''t'') as a function of the driving frequency ''ω'', the amplitude is maximal at the driving frequency
''ω''''r'' is the resonant frequency for this system. Again, note that the resonant frequency does not equal the undamped angular frequency ''ω''0 of the oscillator. They are proportional, and if the damping ratio goes to zero they are the same, but for non-zero damping they are not the same frequency. As shown in the figure, resonance may also occur at other frequencies near the resonant frequency, including ''ω''0, but the maximum response is at the resonant frequency.
Also note that ''ω''''r'' is only real and non-zero if , so this system can only resonate when the harmonic oscillator is significantly underdamped. For systems with a very small damping ratio and a driving frequency near the resonant frequency, the steady state oscillations can become very large.
 Consider a
Consider a
 A sinusoidal input voltage at frequency ''ω'' results in an output voltage at the same frequency that has been scaled by ''G''(''ω'') and has a phase shift ''Φ''(''ω''). The gain and phase can be plotted versus frequency on a Bode plot. For the RLC circuit's capacitor voltage, the gain of the transfer function ''H''(''iω'') is
Note the similarity between the gain here and the amplitude in Equation (). Once again, the gain is maximized at the resonant frequency
Here, the resonance corresponds physically to having a relatively large amplitude for the steady state oscillations of the voltage across the capacitor compared to its amplitude at other driving frequencies.
A sinusoidal input voltage at frequency ''ω'' results in an output voltage at the same frequency that has been scaled by ''G''(''ω'') and has a phase shift ''Φ''(''ω''). The gain and phase can be plotted versus frequency on a Bode plot. For the RLC circuit's capacitor voltage, the gain of the transfer function ''H''(''iω'') is
Note the similarity between the gain here and the amplitude in Equation (). Once again, the gain is maximized at the resonant frequency
Here, the resonance corresponds physically to having a relatively large amplitude for the steady state oscillations of the voltage across the capacitor compared to its amplitude at other driving frequencies.
 A physical system can have as many natural frequencies as it has
A physical system can have as many natural frequencies as it has
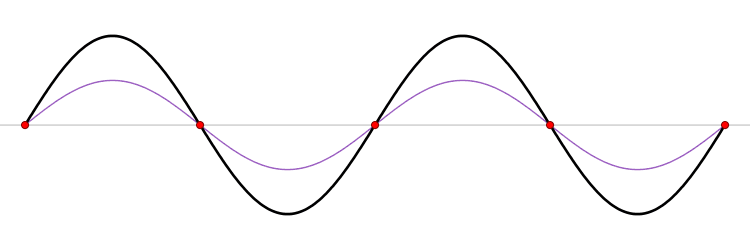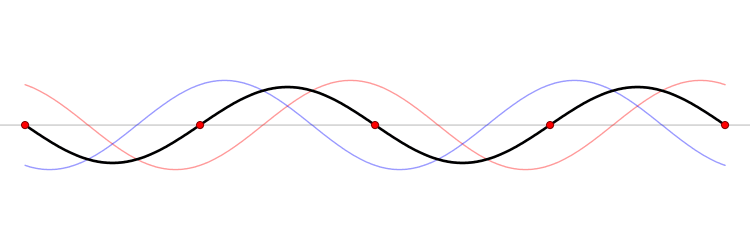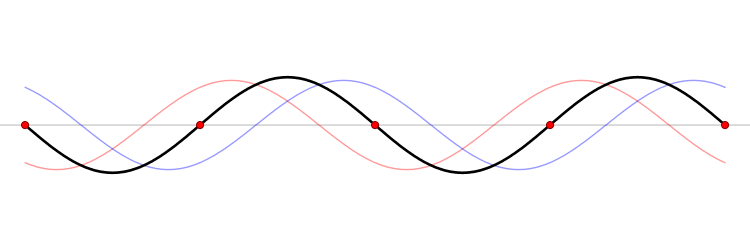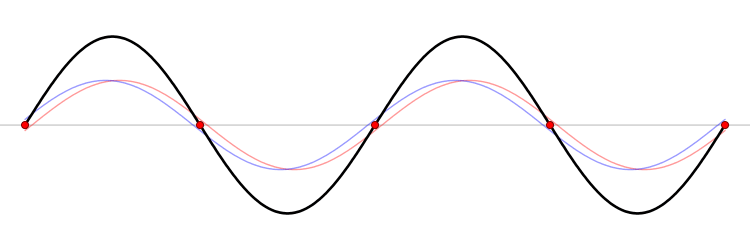 When a string of fixed length is driven at a particular frequency, a wave propagates along the string at the same frequency. The waves reflect off the ends of the string, and eventually a steady state is reached with waves traveling in both directions. The waveform is the superposition of the waves.
At certain frequencies, the steady state waveform does not appear to travel along the string. At fixed positions called
When a string of fixed length is driven at a particular frequency, a wave propagates along the string at the same frequency. The waves reflect off the ends of the string, and eventually a steady state is reached with waves traveling in both directions. The waveform is the superposition of the waves.
At certain frequencies, the steady state waveform does not appear to travel along the string. At fixed positions called
 Mechanical resonance is the tendency of a
Mechanical resonance is the tendency of a
 Nuclear magnetic resonance (NMR) is the name given to a physical resonance phenomenon involving the observation of specific quantum mechanical
Nuclear magnetic resonance (NMR) is the name given to a physical resonance phenomenon involving the observation of specific quantum mechanical
 The ''Q'' factor or ''quality factor'' is a dimensionless parameter that describes how under-damped an
The ''Q'' factor or ''quality factor'' is a dimensionless parameter that describes how under-damped an
 The exact response of a resonance, especially for frequencies far from the resonant frequency, depends on the details of the physical system, and is usually not exactly symmetric about the resonant frequency, as illustrated for the simple harmonic oscillator above.
For a lightly damped linear oscillator with a resonance frequency ''Ω'', the ''intensity'' of oscillations ''I'' when the system is driven with a driving frequency ''ω'' is typically approximated by a formula that is symmetric about the resonance frequency:
Where the susceptibility links the amplitude of the oscillator to the driving force in frequency space:
The intensity is defined as the square of the amplitude of the oscillations. This is a Lorentzian function, or Cauchy distribution, and this response is found in many physical situations involving resonant systems. is a parameter dependent on the damping of the oscillator, and is known as the ''linewidth'' of the resonance. Heavily damped oscillators tend to have broad linewidths, and respond to a wider range of driving frequencies around the resonant frequency. The linewidth is inversely proportional to the ''Q'' factor, which is a measure of the sharpness of the resonance.
In radio engineering and
The exact response of a resonance, especially for frequencies far from the resonant frequency, depends on the details of the physical system, and is usually not exactly symmetric about the resonant frequency, as illustrated for the simple harmonic oscillator above.
For a lightly damped linear oscillator with a resonance frequency ''Ω'', the ''intensity'' of oscillations ''I'' when the system is driven with a driving frequency ''ω'' is typically approximated by a formula that is symmetric about the resonance frequency:
Where the susceptibility links the amplitude of the oscillator to the driving force in frequency space:
The intensity is defined as the square of the amplitude of the oscillations. This is a Lorentzian function, or Cauchy distribution, and this response is found in many physical situations involving resonant systems. is a parameter dependent on the damping of the oscillator, and is known as the ''linewidth'' of the resonance. Heavily damped oscillators tend to have broad linewidths, and respond to a wider range of driving frequencies around the resonant frequency. The linewidth is inversely proportional to the ''Q'' factor, which is a measure of the sharpness of the resonance.
In radio engineering and
The Feynman Lectures on Physics Vol. I Ch. 23: Resonance
- a chapter from an online textbook * Greene, Brian, "
Resonance in strings
'".
Hyperphysics section on resonance concepts
(usage of terms)
demonstrating resonances on a string when the frequency of the driving force is varied
demonstrating the occurrence of resonance when the driving frequency matches with the natural frequency of an oscillator
Breaking glass with sound
including high-speed footage of glass breaking {{Authority control Antennas (radio) Oscillation
 Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force
In physics, a force is an influence that can change the motion of an object. A force can cause an object with mass to change its velocity (e.g. moving from a state of rest), i.e., to accelerate. Force can also be described intuitively as a p ...
(or a Fourier component
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed ...
of it) is equal or close to a natural frequency of the system on which it acts. When an oscillating
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum ...
force is applied at a resonant frequency of a dynamic system, the system will oscillate at a higher amplitude than when the same force is applied at other, non-resonant frequencies.
Frequencies at which the response amplitude is a relative maximum
In mathematical analysis, the maxima and minima (the respective plurals of maximum and minimum) of a function (mathematics), function, known collectively as extrema (the plural of extremum), are the largest and smallest value of the function, e ...
are also known as resonant frequencies or resonance frequencies of the system. Small periodic forces that are near a resonant frequency of the system have the ability to produce large amplitude oscillations in the system due to the storage of vibrational energy
In physics, sound energy is a form of energy that can be heard by living things. Only those waves that have a frequency of 16 Hz to 20 kHz are audible to humans. However, this range is an average and will slightly change from individ ...
.
Resonance phenomena occur with all types of vibrations or waves: there is mechanical resonance, orbital resonance, acoustic resonance
Acoustic resonance is a phenomenon in which an acoustic system amplifies sound waves whose frequency matches one of its own natural frequencies of vibration (its ''resonance frequencies'').
The term "acoustic resonance" is sometimes used to nar ...
, electromagnetic resonance, nuclear magnetic resonance (NMR), electron spin resonance (ESR) and resonance of quantum wave functions. Resonant systems can be used to generate vibrations of a specific frequency (e.g., musical instrument
A musical instrument is a device created or adapted to make musical sounds. In principle, any object that produces sound can be considered a musical instrument—it is through purpose that the object becomes a musical instrument. A person who pl ...
s), or pick out specific frequencies from a complex vibration containing many frequencies (e.g., filters).
The term ''resonance'' (from Latin ''resonantia'', 'echo', from ''resonare'', 'resound') originated from the field of acoustics, particularly the sympathetic resonance observed in musical instruments, e.g., when one string starts to vibrate and produce sound after a different one is struck.
Overview
Resonance occurs when a system is able to store and easily transfer energy between two or more different storage modes (such as kinetic energy and potential energy in the case of a simple pendulum). However, there are some losses from cycle to cycle, calleddamping
Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. In physical systems, damping is produced by processes that dissipate the energy stored in the oscillation. Examples incl ...
. When damping is small, the resonant frequency is approximately equal to the natural frequency of the system, which is a frequency of unforced vibrations. Some systems have multiple, distinct, resonant frequencies.
Examples
 A familiar example is a playground
A familiar example is a playground swing
Swing or swinging may refer to:
Apparatus
* Swing (seat), a hanging seat that swings back and forth
* Pendulum, an object that swings
* Russian swing, a swing-like circus apparatus
* Sex swing, a type of harness for sexual intercourse
* Swing rid ...
, which acts as a pendulum. Pushing a person in a swing in time with the natural interval of the swing (its resonant frequency) makes the swing go higher and higher (maximum amplitude), while attempts to push the swing at a faster or slower tempo produce smaller arcs. This is because the energy the swing absorbs is maximized when the pushes match the swing's natural oscillations.
Resonance occurs widely in nature, and is exploited in many devices. It is the mechanism by which virtually all sinusoidal
A sine wave, sinusoidal wave, or just sinusoid is a mathematical curve defined in terms of the '' sine'' trigonometric function, of which it is the graph. It is a type of continuous wave and also a smooth periodic function. It occurs often in m ...
waves and vibrations are generated. Many sounds we hear, such as when hard objects of metal, glass, or wood are struck, are caused by brief resonant vibrations in the object. Light and other short wavelength electromagnetic radiation is produced by resonance on an atomic scale, such as electrons in atoms. Other examples of resonance:
* Timekeeping mechanisms of modern clocks and watches, e.g., the balance wheel in a mechanical watch and the quartz crystal in a quartz watch
* Tidal resonance of the Bay of Fundy
The Bay of Fundy (french: Baie de Fundy) is a bay between the Canadian provinces of New Brunswick and Nova Scotia, with a small portion touching the U.S. state of Maine. It is an arm of the Gulf of Maine. Its extremely high tidal range is the hi ...
* Acoustic resonance
Acoustic resonance is a phenomenon in which an acoustic system amplifies sound waves whose frequency matches one of its own natural frequencies of vibration (its ''resonance frequencies'').
The term "acoustic resonance" is sometimes used to nar ...
s of musical instruments and the human vocal tract
* Shattering of a crystal wineglass when exposed to a musical tone of the right pitch (its resonant frequency)
* Friction idiophones, such as making a glass object (glass, bottle, vase) vibrate by rubbing around its rim with a fingertip
* Electrical resonance of tuned circuits in radios and TVs that allow radio frequencies to be selectively received
* Creation of coherent
Coherence, coherency, or coherent may refer to the following:
Physics
* Coherence (physics), an ideal property of waves that enables stationary (i.e. temporally and spatially constant) interference
* Coherence (units of measurement), a deri ...
light by optical resonance
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultraviol ...
in a laser cavity
Cavity may refer to:
Biology and healthcare
*Body cavity, a fluid-filled space in many animals where organs typically develop
**Gastrovascular cavity, the primary organ of digestion and circulation in cnidarians and flatworms
*Dental cavity or too ...
* Orbital resonance as exemplified by some moons of the Solar System's gas giants
* Material resonances in atomic scale are the basis of several spectroscopic techniques that are used in condensed matter physics
Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid phases which arise from electromagnetic forces between atoms. More generally, the sub ...
** Electron spin resonance
** Mössbauer effect
** Nuclear magnetic resonance
Linear systems
Resonance manifests itself in many linear and nonlinear systems as oscillations around an equilibrium point. When the system is driven by a sinusoidal external input, a measured output of the system may oscillate in response. The ratio of the amplitude of the output's steady-state oscillations to the input's oscillations is called the gain, and the gain can be a function of the frequency of the sinusoidal external input. Peaks in the gain at certain frequencies correspond to resonances, where the amplitude of the measured output's oscillations are disproportionately large. Since many linear and nonlinear systems that oscillate are modeled asharmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its Mechanical equilibrium, equilibrium position, experiences a restoring force ''F'' Proportionality (mathematics), proportional to the displacement ''x'':
\v ...
s near their equilibria, this section begins with a derivation of the resonant frequency for a driven, damped harmonic oscillator. The section then uses an RLC circuit to illustrate connections between resonance and a system's transfer function, frequency response, poles, and zeroes. Building off the RLC circuit example, the section then generalizes these relationships for higher-order linear systems with multiple inputs and outputs.
The driven, damped harmonic oscillator
Consider a damped mass on a spring driven by a sinusoidal, externally applied force. Newton's second law takes the form where ''m'' is the mass, ''x'' is the displacement of the mass from the equilibrium point, ''F''0 is the driving amplitude, ''ω'' is the driving angular frequency, ''k'' is the spring constant, and ''c'' is the viscous damping coefficient. This can be rewritten in the form where * is called the ''undamped angular frequency of the oscillator'' or the ''natural frequency'', * is called the ''damping ratio''. Many sources also refer to ''ω''0 as the ''resonant frequency''. However, as shown below, when analyzing oscillations of the displacement ''x''(''t''), the resonant frequency is close to but not the same as ''ω''0. In general the resonant frequency is close to but not necessarily the same as the natural frequency. The RLC circuit example in the next section gives examples of different resonant frequencies for the same system. The general solution of Equation () is the sum of atransient
ECHELON, originally a secret government code name, is a surveillance program ( signals intelligence/SIGINT collection and analysis network) operated by the five signatory states to the UKUSA Security Agreement:Given the 5 dialects that ...
solution that depends on initial conditions and a steady state solution that is independent of initial conditions and depends only on the driving amplitude ''F''0, driving frequency ''ω'', undamped angular frequency ''ω''0, and the damping ratio ''ζ''. The transient solution decays in a relatively short amount of time, so to study resonance it is sufficient to consider the steady state solution.
It is possible to write the steady-state solution for ''x''(''t'') as a function proportional to the driving force with an induced phase
Phase or phases may refer to:
Science
*State of matter, or phase, one of the distinct forms in which matter can exist
*Phase (matter), a region of space throughout which all physical properties are essentially uniform
* Phase space, a mathematic ...
change ''φ'',
where
The phase value is usually taken to be between −180° and 0 so it represents a phase lag for both positive and negative values of the arctan argument.
The pendulum
For other driven, damped harmonic oscillators whose equations of motion do not look exactly like the mass on a spring example, the resonant frequency remains but the definitions of ''ω''0 and ''ζ'' change based on the physics of the system. For a pendulum of length ''ℓ'' and small displacement angle ''θ'', Equation () becomes and therefore * *RLC series circuits
circuit
Circuit may refer to:
Science and technology
Electrical engineering
* Electrical circuit, a complete electrical network with a closed-loop giving a return path for current
** Analog circuit, uses continuous signal levels
** Balanced circu ...
consisting of a resistor
A resistor is a passive two-terminal electrical component that implements electrical resistance as a circuit element. In electronic circuits, resistors are used to reduce current flow, adjust signal levels, to divide voltages, bias active el ...
with resistance ''R'', an inductor with inductance ''L'', and a capacitor with capacitance ''C'' connected in series with current ''i''(''t'') and driven by a voltage source with voltage ''v''''in''(''t''). The voltage drop around the circuit is
Rather than analyzing a candidate solution to this equation like in the mass on a spring example above, this section will analyze the frequency response of this circuit. Taking the Laplace transform of Equation (),
where ''I''(''s'') and ''V''''in''(''s'') are the Laplace transform of the current and input voltage, respectively, and ''s'' is a complex frequency parameter in the Laplace domain. Rearranging terms,
Voltage across the capacitor
An RLC circuit in series presents several options for where to measure an output voltage. Suppose the output voltage of interest is the voltage drop across the capacitor. As shown above, in the Laplace domain this voltage is or Define for this circuit a natural frequency and a damping ratio, The ratio of the output voltage to the input voltage becomes ''H''(''s'') is the transfer function between the input voltage and the output voltage. Note that this transfer function has twopoles
Poles,, ; singular masculine: ''Polak'', singular feminine: ''Polka'' or Polish people, are a West Slavic nation and ethnic group, who share a common history, culture, the Polish language and are identified with the country of Poland in Ce ...
–roots of the polynomial in the transfer function's denominator–at
and no zeros–roots of the polynomial in the transfer function's numerator. Moreover, note that for , the magnitude of these poles is the natural frequency ''ω''0 and that for , our condition for resonance in the harmonic oscillator example, the poles are closer to the imaginary axis than to the real axis.
Evaluating ''H''(''s'') along the imaginary axis , the transfer function describes the frequency response of this circuit. Equivalently, the frequency response can be analyzed by taking the Fourier transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, ...
of Equation () instead of the Laplace transform. The transfer function, which is also complex, can be written as a gain and phase,
Voltage across the inductor
The resonant frequency need not always take the form given in the examples above. For the RLC circuit, suppose instead that the output voltage of interest is the voltage across the inductor. As shown above, in the Laplace domain the voltage across the inductor is using the same definitions for ''ω''0 and ''ζ'' as in the previous example. The transfer function between ''V''in(''s'') and this new ''V''out(''s'') across the inductor is Note that this transfer function has the same poles as the transfer function in the previous example, but it also has two zeroes in the numerator at . Evaluating ''H''(''s'') along the imaginary axis, its gain becomes Compared to the gain in Equation () using the capacitor voltage as the output, this gain has a factor of ''ω''2 in the numerator and will therefore have a different resonant frequency that maximizes the gain. That frequency is So for the same RLC circuit but with the voltage across the inductor as the output, the resonant frequency is now ''larger'' than the natural frequency, though it still tends towards the natural frequency as the damping ratio goes to zero. That the same circuit can have different resonant frequencies for different choices of output is not contradictory. As shown in Equation (), the voltage drop across the circuit is divided among the three circuit elements, and each element has different dynamics. The capacitor's voltage grows slowly by integrating the current over time and is therefore more sensitive to lower frequencies, whereas the inductor's voltage grows when the current changes rapidly and is therefore more sensitive to higher frequencies. While the circuit as a whole has a natural frequency where it tends to oscillate, the different dynamics of each circuit element make each element resonate at a slightly different frequency.Voltage across the resistor
Suppose that the output voltage of interest is the voltage across the resistor. In the Laplace domain the voltage across the resistor is and using the same natural frequency and damping ratio as in the capacitor example the transfer function is Note that this transfer function also has the same poles as the previous RLC circuit examples, but it only has one zero in the numerator at ''s'' = 0. For this transfer function, its gain is The resonant frequency that maximizes this gain is and the gain is one at this frequency, so the voltage across the resistor resonates ''at'' the circuit's natural frequency and at this frequency the amplitude of the voltage across the resistor equals the input voltage's amplitude.Antiresonance
Some systems exhibitantiresonance In the physics of coupled oscillators, antiresonance, by analogy with resonance, is a pronounced minimum in the amplitude of an oscillator at a particular frequency, accompanied by a large, abrupt shift in its oscillation phase. Such frequencies are ...
that can be analyzed in the same way as resonance. For antiresonance, the amplitude of the response of the system at certain frequencies is disproportionately ''small'' rather than being disproportionately large. In the RLC circuit example, this phenomenon can be observed by analyzing both the inductor and the capacitor combined.
Suppose that the output voltage of interest in the RLC circuit is the voltage across the inductor ''and'' the capacitor combined in series. Equation () showed that the sum of the voltages across the three circuit elements sums to the input voltage, so measuring the output voltage as the sum of the inductor and capacitor voltages combined is the same as ''v''''in'' minus the voltage drop across the resistor. The previous example showed that at the natural frequency of the system, the amplitude of the voltage drop across the resistor ''equals'' the amplitude of ''v''''in'', and therefore the voltage across the inductor and capacitor combined has zero amplitude. We can show this with the transfer function.
The sum of the inductor and capacitor voltages is
Using the same natural frequency and damping ratios as the previous examples, the transfer function is
Note that this transfer has the same poles as the previous examples but has zeroes at
Evaluating the transfer function along the imaginary axis, its gain is
Rather than look for resonance, i.e., peaks of the gain, notice that the gain goes to zero at ''ω'' = ''ω''0, which complements our analysis of the resistor's voltage. This is called antiresonance, which has the opposite effect of resonance. Rather than result in outputs that are disproportionately large at this frequency, this circuit with this choice of output has no response at all at this frequency. The frequency that is filtered out corresponds exactly to the zeroes of the transfer function, which were shown in Equation () and were on the imaginary axis.
Relationships between resonance and frequency response in the RLC series circuit example
These RLC circuit examples illustrate how resonance is related to the frequency response of the system. Specifically, these examples illustrate: * How resonant frequencies can be found by looking for peaks in the gain of the transfer function between the input and output of the system, for example in a Bode magnitude plot * How the resonant frequency for a single system can be different for different choices of system output * The connection between the system's natural frequency, the system's damping ratio, and the system's resonant frequency * The connection between the system's natural frequency and the magnitude of the transfer function's poles, pointed out in Equation (), and therefore a connection between the poles and the resonant frequency * A connection between the transfer function's zeroes and the shape of the gain as a function of frequency, and therefore a connection between the zeroes and the resonant frequency that maximizes gain * A connection between the transfer function's zeroes and antiresonance The next section extends these concepts to resonance in a general linear system.Generalizing resonance and antiresonance for linear systems
Next consider an arbitrary linear system with multiple inputs and outputs. For example, instate-space representation
In control engineering, a state-space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations or difference equations. State variables are variables wh ...
a third order linear time-invariant system
In system analysis, among other fields of study, a linear time-invariant (LTI) system is a system that produces an output signal from any input signal subject to the constraints of linearity and time-invariance; these terms are briefly define ...
with three inputs and two outputs might be written as
where ''u''''i''(''t'') are the inputs, ''x''''i''(t) are the state variables, ''y''''i''(''t'') are the outputs, and ''A'', ''B'', ''C'', and ''D'' are matrices describing the dynamics between the variables.
This system has a transfer function matrix
In control system theory, and various branches of engineering, a transfer function matrix, or just transfer matrix is a generalisation of the transfer functions of single-input single-output (SISO) systems to multiple-input and multiple-output (M ...
whose elements are the transfer functions between the various inputs and outputs. For example,
Each ''H''''ij''(''s'') is a scalar transfer function linking one of the inputs to one of the outputs. The RLC circuit examples above had one input voltage and showed four possible output voltages–across the capacitor, across the inductor, across the resistor, and across the capacitor and inductor combined in series–each with its own transfer function. If the RLC circuit were set up to measure all four of these output voltages, that system would have a 4×1 transfer function matrix linking the single input to each of the four outputs.
Evaluated along the imaginary axis, each ''H''''ij''(''iω'') can be written as a gain and phase shift,
Peaks in the gain at certain frequencies correspond to resonances between that transfer function's input and output, assuming the system is stable
A stable is a building in which livestock, especially horses, are kept. It most commonly means a building that is divided into separate stalls for individual animals and livestock. There are many different types of stables in use today; the ...
.
Each transfer function ''H''''ij''(''s'') can also be written as a fraction whose numerator and denominator are polynomials of ''s''.
The complex roots of the numerator are called zeroes, and the complex roots of the denominator are called poles. For a stable system, the positions of these poles and zeroes on the complex plane give some indication of whether the system can resonate or antiresonate and at which frequencies. In particular, any stable or marginally stable, complex conjugate pair of poles with imaginary components can be written in terms of a natural frequency and a damping ratio as
as in Equation (). The natural frequency ''ω''0 of that pole is the magnitude of the position of the pole on the complex plane and the damping ratio of that pole determines how quickly that oscillation decays. In general,
* Complex conjugate pairs of ''poles'' near the imaginary axis correspond to a peak or resonance in the frequency response in the vicinity of the pole's natural frequency. If the pair of poles is ''on'' the imaginary axis, the gain is infinite at that frequency.
* Complex conjugate pairs of ''zeroes'' near the imaginary axis correspond to a notch or antiresonance in the frequency response in the vicinity of the zero's frequency, i.e., the frequency equal to the magnitude of the zero. If the pair of zeroes is ''on'' the imaginary axis, the gain is zero at that frequency.
In the RLC circuit example, the first generalization relating poles to resonance is observed in Equation (). The second generalization relating zeroes to antiresonance is observed in Equation (). In the examples of the harmonic oscillator, the RLC circuit capacitor voltage, and the RLC circuit inductor voltage, "poles near the imaginary axis" corresponds to the significantly underdamped condition ζ < 1/.
Standing waves
 A physical system can have as many natural frequencies as it has
A physical system can have as many natural frequencies as it has degrees of freedom
Degrees of freedom (often abbreviated df or DOF) refers to the number of independent variables or parameters of a thermodynamic system. In various scientific fields, the word "freedom" is used to describe the limits to which physical movement or ...
and can resonate near each of those natural frequencies. A mass on a spring, which has one degree of freedom, has one natural frequency. A double pendulum
In physics and mathematics, in the area of dynamical systems, a double pendulum also known as a chaos pendulum is a pendulum with another pendulum attached to its end, forming a simple physical system that exhibits rich dynamic behavior with a ...
, which has two degrees of freedom, can have two natural frequencies. As the number of coupled harmonic oscillators increases, the time it takes to transfer energy from one to the next becomes significant. Systems with very large numbers of degrees of freedom can be thought of as continuous
Continuity or continuous may refer to:
Mathematics
* Continuity (mathematics), the opposing concept to discreteness; common examples include
** Continuous probability distribution or random variable in probability and statistics
** Continuous ...
rather than as having discrete oscillators.
Energy transfers from one oscillator to the next in the form of waves. For example, the string of a guitar or the surface of water in a bowl can be modeled as a continuum of small coupled oscillators and waves can travel along them. In many cases these systems have the potential to resonate at certain frequencies, forming standing wave
In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect ...
s with large-amplitude oscillations at fixed positions. Resonance in the form of standing waves underlies many familiar phenomena, such as the sound produced by musical instruments, electromagnetic cavities used in lasers and microwave ovens, and energy levels of atoms.
Standing waves on a string
 When a string of fixed length is driven at a particular frequency, a wave propagates along the string at the same frequency. The waves reflect off the ends of the string, and eventually a steady state is reached with waves traveling in both directions. The waveform is the superposition of the waves.
At certain frequencies, the steady state waveform does not appear to travel along the string. At fixed positions called
When a string of fixed length is driven at a particular frequency, a wave propagates along the string at the same frequency. The waves reflect off the ends of the string, and eventually a steady state is reached with waves traveling in both directions. The waveform is the superposition of the waves.
At certain frequencies, the steady state waveform does not appear to travel along the string. At fixed positions called nodes
In general, a node is a localized swelling (a "knot") or a point of intersection (a Vertex (graph theory), vertex).
Node may refer to:
In mathematics
*Vertex (graph theory), a vertex in a mathematical graph
*Vertex (geometry), a point where two ...
, the string is never displaced. Between the nodes the string oscillates and exactly halfway between the nodes–at positions called anti-nodes–the oscillations have their largest amplitude.
For a string of length with fixed ends, the displacement of the string perpendicular to the -axis at time is
where
* is the amplitude of the left- and right-traveling waves interfering to form the standing wave,
* is the wave number,
* is the frequency.
The frequencies that resonate and form standing waves relate to the length of the string as
where is the speed of the wave and the integer denotes different modes or harmonic
A harmonic is a wave with a frequency that is a positive integer multiple of the ''fundamental frequency'', the frequency of the original periodic signal, such as a sinusoidal wave. The original signal is also called the ''1st harmonic'', the ...
s. The standing wave with oscillates at the fundamental frequency and has a wavelength that is twice the length of the string. The possible modes of oscillation form a harmonic series.
Types
Mechanical and acoustic
 Mechanical resonance is the tendency of a
Mechanical resonance is the tendency of a mechanical system
A machine is a physical system using Power (physics), power to apply Force, forces and control Motion, movement to perform an action. The term is commonly applied to artificial devices, such as those employing engines or motors, but also to na ...
to absorb more energy when the frequency of its oscillations matches the system's natural frequency of vibration than it does at other frequencies. It may cause violent swaying motions and even catastrophic failure in improperly constructed structures including bridges, buildings, trains, and aircraft. When designing objects, engineers must ensure the mechanical resonance frequencies of the component parts do not match driving vibrational frequencies of motors or other oscillating parts, a phenomenon known as resonance disaster.
Avoiding resonance disasters is a major concern in every building, tower, and bridge construction project. As a countermeasure, shock mount
A shock mount or isolation mount is a mechanical fastener that connects two parts elastically. They are used for shock and vibration isolation.
Isolation mounts allow a piece of equipment to be securely mounted to a foundation and/or frame and, a ...
s can be installed to absorb resonant frequencies and thus dissipate the absorbed energy. The Taipei 101 building relies on a —a tuned mass damper—to cancel resonance. Furthermore, the structure is designed to resonate at a frequency that does not typically occur. Buildings in seismic zones are often constructed to take into account the oscillating frequencies of expected ground motion. In addition, engineers designing objects having engines must ensure that the mechanical resonant frequencies of the component parts do not match driving vibrational frequencies of the motors or other strongly oscillating parts.
Clocks keep time by mechanical resonance in a balance wheel, pendulum, or quartz crystal.
The cadence of runners has been hypothesized to be energetically favorable due to resonance between the elastic energy stored in the lower limb and the mass of the runner.
Acoustic resonance
Acoustic resonance is a phenomenon in which an acoustic system amplifies sound waves whose frequency matches one of its own natural frequencies of vibration (its ''resonance frequencies'').
The term "acoustic resonance" is sometimes used to nar ...
is a branch of mechanical resonance that is concerned with the mechanical vibrations across the frequency range of human hearing, in other words sound. For humans, hearing is normally limited to frequencies between about 20 Hz and 20,000 Hz (20 kHz
The hertz (symbol: Hz) is the unit of frequency in the International System of Units (SI), equivalent to one event (or cycle) per second. The hertz is an SI derived unit whose expression in terms of SI base units is s−1, meaning that on ...
), Many objects and materials act as resonators with resonant frequencies within this range, and when struck vibrate mechanically, pushing on the surrounding air to create sound waves. This is the source of many percussive sounds we hear.
Acoustic resonance is an important consideration for instrument builders, as most acoustic instruments
Instrument may refer to:
Science and technology
* Flight instruments, the devices used to measure the speed, altitude, and pertinent flight angles of various kinds of aircraft
* Laboratory equipment, the measuring tools used in a scientific lab ...
use resonators, such as the strings
String or strings may refer to:
*String (structure), a long flexible structure made from threads twisted together, which is used to tie, bind, or hang other objects
Arts, entertainment, and media Films
* ''Strings'' (1991 film), a Canadian anim ...
and body of a violin, the length of tube in a flute
The flute is a family of classical music instrument in the woodwind group. Like all woodwinds, flutes are aerophones, meaning they make sound by vibrating a column of air. However, unlike woodwind instruments with reeds, a flute is a reedless ...
, and the shape of, and tension on, a drum membrane.
Like mechanical resonance, acoustic resonance can result in catastrophic failure of the object at resonance. The classic example of this is breaking a wine glass with sound at the precise resonant frequency of the glass, although this is difficult in practice.
International Space Station
The rocket engines for the International Space Station (ISS) are controlled by an autopilot. Ordinarily, uploaded parameters for controlling the engine control system for the Zvezda module make the rocket engines boost the International Space Station to a higher orbit. The rocket engines arehinge
A hinge is a mechanical bearing that connects two solid objects, typically allowing only a limited angle of rotation between them. Two objects connected by an ideal hinge rotate relative to each other about a fixed axis of rotation: all other ...
-mounted, and ordinarily the crew doesn't notice the operation. On January 14, 2009, however, the uploaded parameters made the autopilot swing the rocket engines in larger and larger oscillations, at a frequency of 0.5 Hz. These oscillations were captured on video, and lasted for 142 seconds.
Electrical
Electrical resonance occurs in an electric circuit at a particular ''resonant frequency'' when the impedance of the circuit is at a minimum in a series circuit or at maximum in a parallel circuit (usually when the transfer function peaks in absolute value). Resonance in circuits are used for both transmitting and receiving wireless communications such as television, cell phones and radio.Optical
Anoptical cavity An optical cavity, resonating cavity or optical resonator is an arrangement of mirrors or other optical elements that forms a cavity resonator for light waves. Optical cavities are a major component of lasers, surrounding the gain medium and provi ...
, also called an ''optical resonator'', is an arrangement of mirrors that forms a standing wave cavity resonator for light wave
In physics, electromagnetic radiation (EMR) consists of waves of the electromagnetic (EM) field, which propagate through space and carry momentum and electromagnetic radiant energy. It includes radio waves, microwaves, infrared, (visible) ligh ...
s. Optical cavities are a major component of lasers, surrounding the gain medium and providing feedback
Feedback occurs when outputs of a system are routed back as inputs as part of a chain of cause-and-effect that forms a circuit or loop. The system can then be said to ''feed back'' into itself. The notion of cause-and-effect has to be handled ...
of the laser light. They are also used in optical parametric oscillators and some interferometer
Interferometry is a technique which uses the ''interference'' of superimposed waves to extract information. Interferometry typically uses electromagnetic waves and is an important investigative technique in the fields of astronomy, fiber op ...
s. Light confined in the cavity reflects multiple times producing standing waves for certain resonant frequencies. The standing wave patterns produced are called "modes". Longitudinal modes differ only in frequency while transverse modes differ for different frequencies and have different intensity patterns across the cross-section of the beam. Ring resonators and whispering galleries are examples of optical resonators that do not form standing waves.
Different resonator types are distinguished by the focal lengths of the two mirrors and the distance between them; flat mirrors are not often used because of the difficulty of aligning them precisely. The geometry (resonator type) must be chosen so the beam remains stable, i.e., the beam size does not continue to grow with each reflection. Resonator types are also designed to meet other criteria such as minimum beam waist or having no focal point (and therefore intense light at that point) inside the cavity.
Optical cavities are designed to have a very large ''Q'' factor. A beam reflects a large number of times with little attenuation—therefore the frequency line width of the beam is small compared to the frequency of the laser.
Additional optical resonances are guided-mode resonance
Guided-mode resonance or waveguide-mode resonance is a phenomenon wherein the guided modes of an optical waveguide can be excited and simultaneously extracted by the introduction of a phase-matching element, such as a diffraction grating or prism. ...
s and surface plasmon resonance, which result in anomalous reflection and high evanescent fields at resonance. In this case, the resonant modes are guided modes of a waveguide or surface plasmon modes of a dielectric-metallic interface. These modes are usually excited by a subwavelength grating.
Orbital
In celestial mechanics, an orbital resonance occurs when two orbiting bodies exert a regular, periodic gravitational influence on each other, usually due to their orbital periods being related by a ratio of two small integers. Orbital resonances greatly enhance the mutual gravitational influence of the bodies. In most cases, this results in an ''unstable'' interaction, in which the bodies exchange momentum and shift orbits until the resonance no longer exists. Under some circumstances, a resonant system can be stable and self-correcting, so that the bodies remain in resonance. Examples are the 1:2:4 resonance of Jupiter's moons Ganymede,Europa
Europa may refer to:
Places
* Europe
* Europa (Roman province), a province within the Diocese of Thrace
* Europa (Seville Metro), Seville, Spain; a station on the Seville Metro
* Europa City, Paris, France; a planned development
* Europa Cliff ...
, and Io, and the 2:3 resonance between Pluto and Neptune
Neptune is the eighth planet from the Sun and the farthest known planet in the Solar System. It is the fourth-largest planet in the Solar System by diameter, the third-most-massive planet, and the densest giant planet. It is 17 times ...
. Unstable resonances with Saturn
Saturn is the sixth planet from the Sun and the second-largest in the Solar System, after Jupiter. It is a gas giant with an average radius of about nine and a half times that of Earth. It has only one-eighth the average density of Earth; h ...
's inner moons give rise to gaps in the rings of Saturn. The special case of 1:1 resonance (between bodies with similar orbital radii) causes large Solar System bodies to clear the neighborhood around their orbits by ejecting nearly everything else around them; this effect is used in the current definition of a planet
The definition of ''planet'', since the word was coined by the ancient Greeks, has included within its scope a wide range of celestial bodies. Greek astronomy, Greek astronomers employed the term (), 'wandering stars', for star-like objects wh ...
.
Atomic, particle, and molecular
 Nuclear magnetic resonance (NMR) is the name given to a physical resonance phenomenon involving the observation of specific quantum mechanical
Nuclear magnetic resonance (NMR) is the name given to a physical resonance phenomenon involving the observation of specific quantum mechanical magnetic
Magnetism is the class of physical attributes that are mediated by a magnetic field, which refers to the capacity to induce attractive and repulsive phenomena in other entities. Electric currents and the magnetic moments of elementary particle ...
properties of an atomic nucleus
Nucleus ( : nuclei) is a Latin word for the seed inside a fruit. It most often refers to:
*Atomic nucleus, the very dense central region of an atom
*Cell nucleus, a central organelle of a eukaryotic cell, containing most of the cell's DNA
Nucle ...
in the presence of an applied, external magnetic field. Many scientific techniques exploit NMR phenomena to study molecular physics, crystals, and non-crystalline materials through NMR spectroscopy. NMR is also routinely used in advanced medical imaging techniques, such as in magnetic resonance imaging
Magnetic resonance imaging (MRI) is a medical imaging technique used in radiology to form pictures of the anatomy and the physiological processes of the body. MRI scanners use strong magnetic fields, magnetic field gradients, and radio wave ...
(MRI).
All nuclei containing odd numbers of nucleons have an intrinsic magnetic moment and angular momentum. A key feature of NMR is that the resonant frequency of a particular substance is directly proportional to the strength of the applied magnetic field. It is this feature that is exploited in imaging techniques; if a sample is placed in a non-uniform magnetic field then the resonant frequencies of the sample's nuclei depend on where in the field they are located. Therefore, the particle can be located quite precisely by its resonant frequency.
Electron paramagnetic resonance, otherwise known as ''electron spin resonance'' (ESR), is a spectroscopic technique similar to NMR, but uses unpaired electrons instead. Materials for which this can be applied are much more limited since the material needs to both have an unpaired spin and be paramagnetic.
The Mössbauer effect is the resonant and recoil-free emission and absorption of gamma ray photons by atoms bound in a solid form.
Resonance in particle physics appears in similar circumstances to classical physics
Classical physics is a group of physics theories that predate modern, more complete, or more widely applicable theories. If a currently accepted theory is considered to be modern, and its introduction represented a major paradigm shift, then the ...
at the level of quantum mechanics and quantum field theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines classical field theory, special relativity, and quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and ...
. Resonances can also be thought of as unstable particles, with the formula in the Universal resonance curve section of this article applying if ''Γ'' is the particle's decay rate
Radioactive decay (also known as nuclear decay, radioactivity, radioactive disintegration, or nuclear disintegration) is the process by which an unstable atomic nucleus loses energy by radiation. A material containing unstable nuclei is consid ...
and ''Ω'' is the particle's mass ''M''. In that case, the formula comes from the particle's propagator
In quantum mechanics and quantum field theory, the propagator is a function that specifies the probability amplitude for a particle to travel from one place to another in a given period of time, or to travel with a certain energy and momentum. In ...
, with its mass replaced by the complex number ''M'' + ''iΓ''. The formula is further related to the particle's decay rate by the optical theorem
In physics, the optical theorem is a general law of wave scattering theory, which relates the forward scattering amplitude to the total cross section of the scatterer. It is usually written in the form
:\sigma_\mathrm=\frac~\mathrm\,f(0),
where (0 ...
.
Disadvantages
A column of soldiers marching in regular step on a narrow and structurally flexible bridge can set it into dangerously large amplitude oscillations. April 12, 1831, theBroughton Suspension Bridge
Broughton Suspension Bridge was an iron chain suspension bridge built in 1826 to span the River Irwell between Broughton and Pendleton, now in Salford, Greater Manchester, England. One of Europe's first suspension bridges, it has been attrib ...
near Salford, England
Salford () is a city and the largest settlement in the City of Salford metropolitan borough in Greater Manchester, England. In 2011, Salford had a population of 103,886. It is also the second and only other city in the metropolitan county afte ...
collapsed while a group of British soldiers were marching across. Since then, the British Army has had a standing order for soldiers to break stride when marching across bridges, to avoid resonance from their regular marching pattern affecting the bridge.
Vibrations of a motor or engine can induce resonant vibration in its supporting structures if their natural frequency is close to that of the vibrations of the engine. A common example is the rattling sound of a bus body when the engine is left idling.
Structural resonance of a suspension bridge induced by winds can lead to its catastrophic collapse. Several early suspension bridges in Europe and USA
The United States of America (U.S.A. or USA), commonly known as the United States (U.S. or US) or America, is a country Continental United States, primarily located in North America. It consists of 50 U.S. state, states, a Washington, D.C., ...
were destroyed by structural resonance induced by modest winds. The collapse of the Tacoma Narrows Bridge on 7 November 1940 is characterized in physics as a classic example of resonance. It has been argued by Robert H. Scanlan
Robert H. Scanlan (1914-2001) was an American civil and aeronautical engineer who came to be widely recognized as a leader in the analysis of wind effects on large structures. Scanlan created the concept of flutter derivatives to aid in the repres ...
and others that the destruction was instead caused by aeroelastic flutter, a complicated interaction between the bridge and the winds passing through it—an example of a self oscillation
Self-oscillation is the generation and maintenance of a periodic motion by a source of power that lacks any corresponding periodicity. The oscillator itself controls the phase with which the external power acts on it. Self-oscillators are therefor ...
, or a kind of "self-sustaining vibration" as referred to in the nonlinear theory of vibrations.
Q factor
oscillator
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum ...
or resonator is, and characterizes the bandwidth of a resonator relative to its center frequency.
A high value for ''Q'' indicates a lower rate of energy loss relative to the stored energy, i.e., the system is lightly damped. The parameter is defined by the equation:
.
The higher the Q factor, the greater the amplitude at the resonant frequency, and the smaller the ''bandwidth'', or range of frequencies around resonance occurs. In electrical resonance, a high-''Q'' circuit in a radio receiver is more difficult to tune, but has greater selectivity
Selectivity may refer to:
Psychology and behaviour
* Choice, making a selection among options
* Discrimination, the ability to recognize differences
* Socioemotional selectivity theory, in social psychology
Engineering
* Selectivity (radio), a ...
, and so would be better at filtering out signals from other stations. High Q oscillators are more stable.
Examples that normally have a low Q factor include door closers (Q=0.5). Systems with high Q factors include tuning forks (Q=1000), atomic clocks and lasers (Q≈1011).
Universal resonance curve
electronics engineering
Electronics engineering is a sub-discipline of electrical engineering which emerged in the early 20th century and is distinguished by the additional use of active components such as semiconductor devices to amplify and control electric current f ...
, this approximate symmetric response is known as the ''universal resonance curve'', a concept introduced by Frederick E. Terman in 1932 to simplify the approximate analysis of radio circuits with a range of center frequencies and ''Q'' values.
See also
*Cymatics
Cymatics (from grc, κῦμα, translit=kyma, translation=wave) is a subset of modal vibrational phenomena. The term was coined by Hans Jenny (1904-1972), a Swiss follower of the philosophical school known as anthroposophy. Typically the surf ...
* Driven harmonic motion
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force ''F'' proportional to the displacement ''x'':
\vec F = -k \vec x,
where ''k'' is a positive consta ...
* Earthquake engineering
Earthquake engineering is an interdisciplinary branch of engineering that designs and analyzes structures, such as buildings and bridges, with earthquakes in mind. Its overall goal is to make such structures more resistant to earthquakes. An earth ...
* Electric dipole spin resonance
* Formant
* Limbic resonance
Limbic resonance is the idea that the capacity for sharing deep emotional states arises from the limbic system of the brain. These states include the dopamine circuit-promoted feelings of empathic harmony, and the norepinephrine circuit-originated ...
* Nonlinear resonance
* Normal mode
A normal mode of a dynamical system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The free motion described by the normal modes takes place at fixed frequencies. ...
* Positive feedback
* Schumann resonance
* Simple harmonic motion
* Stochastic resonance
Stochastic resonance (SR) is a phenomenon in which a signal that is normally too weak to be detected by a sensor, can be boosted by adding white noise to the signal, which contains a wide spectrum of frequencies. The frequencies in the white no ...
* Sympathetic string
Notes
References
* * * * * * * * * * * * * *External links
The Feynman Lectures on Physics Vol. I Ch. 23: Resonance
- a chapter from an online textbook * Greene, Brian, "
Resonance in strings
'".
The Elegant Universe
''The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory'' is a book by Brian Greene published in 1999, which introduces string and superstring theory, and provides a comprehensive though non-technical asses ...
, NOVA
A nova (plural novae or novas) is a transient astronomical event that causes the sudden appearance of a bright, apparently "new" star (hence the name "nova", which is Latin for "new") that slowly fades over weeks or months. Causes of the dramati ...
( PBS)Hyperphysics section on resonance concepts
(usage of terms)
demonstrating resonances on a string when the frequency of the driving force is varied
demonstrating the occurrence of resonance when the driving frequency matches with the natural frequency of an oscillator
Breaking glass with sound
including high-speed footage of glass breaking {{Authority control Antennas (radio) Oscillation