|
Antiresonance
In the physics of coupled oscillators, antiresonance, by analogy with resonance, is a pronounced minimum in the amplitude of an oscillator at a particular frequency, accompanied by a large, abrupt shift in its oscillation phase. Such frequencies are known as the system's antiresonant frequencies, and at these frequencies the oscillation amplitude can drop to almost zero. Antiresonances are caused by destructive interference, for example between an external driving force and interaction with another oscillator. Antiresonances can occur in all types of coupled oscillator systems, including mechanical, acoustical, electromagnetic, and quantum systems. They have important applications in the characterization of complicated coupled systems. The term ''antiresonance'' is used in electrical engineering for a form of resonance in a single oscillator with similar effects. Antiresonance in electrical engineering In electrical engineering, antiresonance is the condition for which th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Resonance
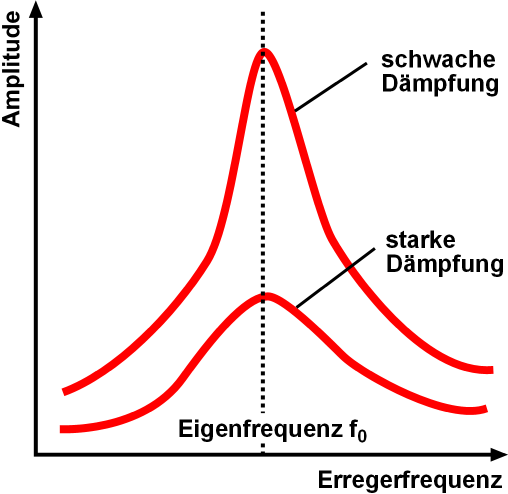
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied Periodic function, periodic force (or a Fourier analysis, Fourier component of it) is equal or close to a natural frequency of the system on which it acts. When an Oscillation, oscillating force is applied at a resonant frequency of a dynamic system, the system will oscillate at a higher Amplitude, amplitude than when the same force is applied at other, non-resonant frequencies. Frequencies at which the response amplitude is a relative maximum are also known as resonant frequencies or resonance frequencies of the system. Small periodic forces that are near a resonant frequency of the system have the ability to produce large amplitude oscillations in the system due to the storage of vibrational energy. Resonance phenomena occur with all types of vibrations or waves: there is mechanical resonance, orbital resonance, acoustic resonance, Electromagnetic radiation, electromagnet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
RLC Circuit
An RLC circuit is an electrical circuit consisting of a resistor (R), an inductor (L), and a capacitor (C), connected in series or in parallel. The name of the circuit is derived from the letters that are used to denote the constituent components of this circuit, where the sequence of the components may vary from RLC. The circuit forms a harmonic oscillator for current, and resonates in a manner similar to an LC circuit. Introducing the resistor increases the decay of these oscillations, which is also known as damping. The resistor also reduces the peak resonant frequency. Some resistance is unavoidable even if a resistor is not specifically included as a component. RLC circuits have many applications as oscillator circuits. Radio receivers and television sets use them for tuning to select a narrow frequency range from ambient radio waves. In this role, the circuit is often referred to as a tuned circuit. An RLC circuit can be used as a band-pass filter, band-stop filter, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." Physics is one of the most fundamental scientific disciplines, with its main goal being to understand how the universe behaves. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
LC Circuit
An LC circuit, also called a resonant circuit, tank circuit, or tuned circuit, is an electric circuit consisting of an inductor, represented by the letter L, and a capacitor, represented by the letter C, connected together. The circuit can act as an electrical resonator, an electrical analogue of a tuning fork, storing energy oscillating at the circuit's resonant frequency. LC circuits are used either for generating signals at a particular frequency, or picking out a signal at a particular frequency from a more complex signal; this function is called a bandpass filter. They are key components in many electronic devices, particularly radio equipment, used in circuits such as oscillators, filters, tuners and frequency mixers. An LC circuit is an idealized model since it assumes there is no dissipation of energy due to resistance. Any practical implementation of an LC circuit will always include loss resulting from small but non-zero resistance within the components and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Frequency
In physics, angular frequency "''ω''" (also referred to by the terms angular speed, circular frequency, orbital frequency, radian frequency, and pulsatance) is a scalar measure of rotation rate. It refers to the angular displacement per unit time (for example, in rotation) or the rate of change of the phase of a sinusoidal waveform (for example, in oscillations and waves), or as the rate of change of the argument of the sine function. Angular frequency (or angular speed) is the magnitude of the pseudovector quantity angular velocity.(UP1) One turn is equal to 2''π'' radians, hence \omega = \frac = , where: *''ω'' is the angular frequency (unit: radians per second), *''T'' is the period (unit: seconds), *''f'' is the ordinary frequency (unit: hertz) (sometimes ''ν''). Units In SI units, angular frequency is normally presented in radians per second, even when it does not express a rotational value. The unit hertz (Hz) is dimensionally equivalent, but by conventi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotating Wave Approximation
The rotating-wave approximation is an approximation used in atom optics and magnetic resonance. In this approximation, terms in a Hamiltonian that oscillate rapidly are neglected. This is a valid approximation when the applied electromagnetic radiation is near resonance with an atomic transition, and the intensity is low. Explicitly, terms in the Hamiltonians that oscillate with frequencies \omega_L + \omega_0 are neglected, while terms that oscillate with frequencies \omega_L - \omega_0 are kept, where \omega_L is the light frequency, and \omega_0 is a transition frequency. The name of the approximation stems from the form of the Hamiltonian in the interaction picture, as shown below. By switching to this picture the evolution of an atom due to the corresponding atomic Hamiltonian is absorbed into the system ket, leaving only the evolution due to the interaction of the atom with the light field to consider. It is in this picture that the rapidly oscillating terms mentioned prev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number a+bi, is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with rea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Damping Ratio
Damping is an influence within or upon an oscillator, oscillatory system that has the effect of reducing or preventing its oscillation. In physical systems, damping is produced by processes that dissipate the energy stored in the oscillation. Examples include Viscosity, viscous Drag (physics), drag (a liquid's viscosity can hinder an oscillatory system, causing it to slow down; see viscous damping) in mechanical systems, Electrical resistance and conductance, resistance in electronic oscillators, and absorption and scattering of light in optical oscillators. Damping not based on energy loss can be important in other oscillating systems such as those that occur in ecology, biological systems and Bicycle_and_motorcycle_dynamics#Lateral_motion_theory, bikes (ex. Suspension (mechanics)). Not to be confused with friction, which is a dissipative force acting on a system. Friction can cause or be a factor of damping. The damping ratio is a dimensionless measure describing how Harmonic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Differential Equation
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contrast with the term partial differential equation which may be with respect to ''more than'' one independent variable. Differential equations A linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y +a_1(x)y' + a_2(x)y'' +\cdots +a_n(x)y^+b(x)=0, where , ..., and are arbitrary differentiable functions that do not need to be linear, and are the successive derivatives of the unknown function of the variable . Among ordinary differential equations, linear differential equations play a prominent role for several reasons. Most elementary and special functions that are encountered in physics and applied mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging back and forth. The time for one complete cycle, a left swing and a right swing, is called the period. The period depends on the length of the pendulum and also to a slight degree on the amplitude, the width of the pendulum's swing. From the first scientific investigations of the pendulum around 1602 by Galileo Galilei, the regular motion of pendulums was used for timekeeping and was the world's most accurate timekeeping technology until the 1930s. The pendulum clock invented by Christiaan Huygens in 1658 became the world's standard timekeeper, used in homes and offices for 270 years, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Oscillators
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force ''F'' proportional to the displacement ''x'': \vec F = -k \vec x, where ''k'' is a positive constant. If ''F'' is the only force acting on the system, the system is called a simple harmonic oscillator, and it undergoes simple harmonic motion: sinusoidal oscillations about the equilibrium point, with a constant amplitude and a constant frequency (which does not depend on the amplitude). If a frictional force (damping) proportional to the velocity is also present, the harmonic oscillator is described as a damped oscillator. Depending on the friction coefficient, the system can: * Oscillate with a frequency lower than in the undamped case, and an amplitude decreasing with time (underdamped oscillator). * Decay to the equilibrium position, without oscillations (overdamped oscillator). The boundary solution between an underdamped oscillat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |