Rectified 16-cell

In geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called C₂₄, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, octacube, hyper-diamond or polyoctahedron, being constructed of octahedral cells.

The boundary of the 24-cell is composed of 24 octahedral cells with six meeting at each vertex, and three at each edge. Together they have 96 triangular faces, 96 edges, and 24 vertices. The vertex figure is a cube. The 24-cell is self-dual. It and the tesseract are the only convex regular 4-polytopes in which the edge length equals the radius.

The 24-cell does not have a regular analogue in 3 dimensions. It is the only one of the six convex regular 4-polytopes which is not the four-dimensional analogue of one of the five regular Platonic solids. However, it can be seen as the analogue of a pair of irregular solids: the cuboctahedron and its dual the rhombic dodecahedron.

Translated copies of the 24-cell can tile four-dimensional space face-to-face, forming the 24-cell honeycomb. As a polytope that can tile by translation, the 24-cell is an example of a parallelotope, the simplest one that is not also a zonotope.

Geometry

The 24-cell incorporates the geometries of every convex regular polytope in the first four dimensions, except the 5-cell, those with a 5 in their Schlӓfli symbol, and the polygons and above. It is especially useful to explore the 24-cell, because one can see the geometric relationships among all of these regular polytopes in a single 24-cell or its honeycomb.

The 24-cell is the fourth in the sequence of 6 convex regular 4-polytopes (in order of size and complexity). It can be deconstructed into 3 overlapping instances of its predecessor the tesseract (8-cell), as the 8-cell can be deconstructed into 2 overlapping instances of its predecessor the 16-cell. The reverse procedure to construct each of these from an instance of its predecessor preserves the radius of the predecessor, but generally produces a successor with a smaller edge length.

Coordinates

Squares

The 24-cell is the convex hull of its vertices which can be described as the 24 coordinate permutations of:

:$(\pm1, \pm 1, 0, 0) \in \mathbb^4$.

Those coordinates can be constructed as , rectifying the 16-cell with 8 vertices permutations of (±2,0,0,0). The vertex figure of a 16-cell is the octahedron; thus, cutting the vertices of the 16-cell at the midpoint of its incident edges produces 8 octahedral cells. This process also rectifies the tetrahedral cells of the 16-cell which become 16 octahedra, giving the 24-cell 24 octahedral cells.

In this frame of reference the 24-cell has edges of length and is inscribed in a 3-sphere of radius . Remarkably, the edge length equals the circumradius, as in the hexagon, or the cuboctahedron. Such polytopes are ''radially equilateral''.

The 24 vertices form 18 great squares (3 sets of 6 orthogonal central squares), 3 of which intersect at each vertex. By viewing just one square at each vertex, the 24-cell can be seen as the vertices of 3 pairs of completely orthogonal great squares which intersect at no vertices.

Hexagons

The 24-cell is self-dual, having the same number of vertices (24) as cells and the same number of edges (96) as faces.

If the dual of the above 24-cell of edge length is taken by reciprocating it about its ''inscribed'' sphere, another 24-cell is found which has edge length and circumradius 1, and its coordinates reveal more structure. In this frame of reference the 24-cell lies vertex-up, and its vertices can be given as follows:

8 vertices obtained by permuting the ''integer'' coordinates:

: (±1, 0, 0, 0)

and 16 vertices with ''half-integer'' coordinates of the form:
:(±, ±, ±, ±)

all 24 of which lie at distance 1 from the origin.

Viewed as quaternions, these are the unit Hurwitz quaternions.

The 24-cell has unit radius and unit edge length in this coordinate system. We refer to the system as ''unit radius coordinates'' to distinguish it from others, such as the radius coordinates used above.

The 24 vertices and 96 edges form 16 non-orthogonal great hexagons, four of which intersect at each vertex. By viewing just one hexagon at each vertex, the 24-cell can be seen as the 24 vertices of 4 non-intersecting hexagonal great circles which are Clifford parallel to each other.

The 12 axes and 16 hexagons of the 24-cell constitute a Reye configuration, which in the language of configurations is written as 12₄16₃ to indicate that each axis belongs to 4 hexagons, and each hexagon contains 3 axes.

Triangles

The 24 vertices form 32 equilateral great triangles, of edge length in the unit-radius 24-cell, inscribed in the 16 great hexagons. Each great triangle is a ring linking three completely disjoint great squares.

Hypercubic chords

The 24 vertices of the 24-cell are distributed at four different chord lengths from each other: , , and .

Each vertex is joined to 8 others by an edge of length 1, spanning 60° = of arc. Next nearest are 6 vertices located 90° = away, along an interior chord of length . Another 8 vertices lie 120° = away, along an interior chord of length . The opposite vertex is 180° = away along a diameter of length 2. Finally, as the 24-cell is radially equilateral, its center can be treated as a 25th canonical apex vertex, which is 1 edge length away from all the others.

To visualize how the interior polytopes of the 24-cell fit together (as described below), keep in mind that the four chord lengths (, , , ) are the long diameters of the hypercubes of dimensions 1 through 4: the long diameter of the square is ; the long diameter of the cube is ; and the long diameter of the tesseract is . Moreover, the long diameter of the octahedron is like the square; and the long diameter of the 24-cell itself is like the tesseract. In the 24-cell, the chords are the edges of central squares, and the chords are the diagonals of central squares.

Geodesics

The vertex chords of the 24-cell are arranged in geodesic great circle polygons. The geodesic distance between two 24-cell vertices along a path of edges is always 1, 2, or 3, and it is 3 only for opposite vertices.

The edges occur in 16 hexagonal great circles (in planes inclined at 60 degrees to each other), 4 of which cross at each vertex. The 96 distinct edges divide the surface into 96 triangular faces and 24 octahedral cells: a 24-cell. The 16 hexagonal great circles can be divided into 4 sets of 4 non-intersecting Clifford parallel geodesics, such that only one hexagonal great circle in each set passes through each vertex, and the 4 hexagons in each set reach all 24 vertices.

The chords occur in 18 square great circles (3 sets of 6 orthogonal planes), 3 of which cross at each vertex. The 72 distinct chords do not run in the same planes as the hexagonal great circles; they do not follow the 24-cell's edges, they pass through its octagonal cell centers. The 72 chords are the 3 orthogonal axes of the 24 octahedral cells, joining vertices which are 2 edges apart. The 18 square great circles can be divided into 3 sets of 6 non-intersecting Clifford parallel geodesics, such that only one square great circle in each set passes through each vertex, and the 6 squares in each set reach all 24 vertices.

The chords occur in 32 triangular great circles in 16 planes, 4 of which cross at each vertex. The 96 distinct chords run vertex-to-every-other-vertex in the same planes as the hexagonal great circles. They are the 3 edges of the 32 great triangles inscribed in the 16 great hexagons, joining vertices which are 2 edges apart on a great circle.

The chords occur as 12 vertex-to-vertex diameters (3 sets of 4 orthogonal axes), the 24 radii around the 25th central vertex.

The sum of the squared lengths of all these distinct chords of the 24-cell is 576 = 24². These are all the central polygons through vertices, but in 4-space there are geodesics on the 3-sphere which do not lie in central planes at all. There are geodesic shortest paths between two 24-cell vertices that are helical rather than simply circular; they corresponding to diagonal isoclinic rotations rather than simple rotations.

The edges occur in 48 parallel pairs, apart. The chords occur in 36 parallel pairs, apart. The chords occur in 48 parallel pairs, apart.

The central planes of the 24-cell can be divided into 4 central hyperplanes (3-spaces) each forming a cuboctahedron. The great hexagons are 60 degrees apart; the great squares are 90 degrees or 60 degrees apart; a great square and a great hexagon are 90 degrees ''and'' 60 degrees apart. Each set of similar central polygons (squares or hexagons) can be divided into 4 sets of non-intersecting Clifford parallel polygons (of 6 squares or 4 hexagons). Each set of Clifford parallel great circles is a parallel fiber bundle which visits all 24 vertices just once.

Each great circle intersects with the other great circles to which it is not Clifford parallel at one diameter of the 24-cell. Great circles which are completely orthogonal or otherwise Clifford parallel do not intersect at all: they pass through disjoint sets of vertices.

Constructions

Triangles and squares come together uniquely in the 24-cell to generate, as interior features, all of the triangle-faced and square-faced regular convex polytopes in the first four dimensions (with caveats for the 5-cell and the 600-cell). Consequently, there are numerous ways to construct or deconstruct the 24-cell.

Reciprocal constructions from 8-cell and 16-cell

The 8 integer vertices (±1, 0, 0, 0) are the vertices of a regular 16-cell, and the 16 half-integer vertices (±, ±, ±, ±) are the vertices of its dual, the tesseract (8-cell). The tesseract gives Gosset's construction of the 24-cell, equivalent to cutting a tesseract into 8 cubic pyramids, and then attaching them to the facets of a second tesseract. The analogous construction in 3-space gives the rhombic dodecahedron which, however, is not regular. The 16-cell gives the reciprocal construction of the 24-cell, Cesaro's construction, equivalent to rectifying a 16-cell (truncating its corners at the mid-edges, as described above). The analogous construction in 3-space gives the cuboctahedron (dual of the rhombic dodecahedron) which, however, is not regular. The tesseract and the 16-cell are the only regular 4-polytopes in the 24-cell.

We can further divide the 16 half-integer vertices into two groups: those whose coordinates contain an even number of minus (−) signs and those with an odd number. Each of these groups of 8 vertices also define a regular 16-cell. This shows that the vertices of the 24-cell can be grouped into three disjoint sets of eight with each set defining a regular 16-cell, and with the complement defining the dual tesseract. This also shows that the symmetries of the 16-cell form a subgroup of index 3 of the symmetry group of the 24-cell.

Diminishings

We can facet the 24-cell by cutting through interior cells bounded by vertex chords to remove vertices, exposing the facets of interior 4-polytopes inscribed in the 24-cell. One can cut a 24-cell through any planar hexagon of 6 vertices, any planar rectangle of 4 vertices, or any triangle of 3 vertices. The great circle central planes ( above) are only some of those planes. Here we shall expose some of the others: the face planes of interior polytopes.

= 8-cell

=
Starting with a complete 24-cell, remove 8 orthogonal vertices (4 opposite pairs on 4 perpendicular axes), and the 8 edges which radiate from each, by cutting through 8 cubic cells bounded by edges to remove 8 cubic pyramids whose apexes are the vertices to be removed. This removes 4 edges from each hexagonal great circle (retaining just one opposite pair of edges), so no continuous hexagonal great circles remain. Now 3 perpendicular edges meet and form the corner of a cube at each of the 16 remaining vertices, and the 32 remaining edges divide the surface into 24 square faces and 8 cubic cells: a tesseract. There are three ways you can do this (choose a set of 8 orthogonal vertices out of 24), so there are three such tesseracts inscribed in the 24-cell. They overlap with each other, but most of their element sets are disjoint: they share some vertex count, but no edge length, face area, or cell volume. They do share 4-content, their common core.

= 16-cell

=
Starting with a complete 24-cell, remove the 16 vertices of a tesseract (retaining the 8 vertices you removed above), by cutting through 16 tetrahedral cells bounded by chords to remove 16 tetrahedral pyramids whose apexes are the vertices to be removed. This removes 12 great squares (retaining just one orthogonal set) and all the edges, exposing chords as the new edges. Now the remaining 6 great squares cross perpendicularly, 3 at each of 8 remaining vertices, and their 24 edges divide the surface into 32 triangular faces and 16 tetrahedral cells: a 16-cell. There are three ways you can do this (remove 1 of 3 sets of tesseract vertices), so there are three such 16-cells inscribed in the 24-cell. They overlap with each other, but all of their element sets are disjoint: they do not share any vertex count, edge length, or face area, but they do share cell volume. They also share 4-content, their common core.

Tetrahedral constructions

The 24-cell can be constructed radially from 96 equilateral triangles of edge length which meet at the center of the polytope, each contributing two radii and an edge. They form 96 tetrahedra (each contributing one 24-cell face), all sharing the 25th central apex vertex. These form 24 octahedral pyramids (half-16-cells) with their apexes at the center.

The 24-cell can be constructed from 96 equilateral triangles of edge length , where the three vertices of each triangle are located 90° = away from each other on the 3-sphere. They form 48 tetrahedra (the cells of the three 16-cells), centered at the 24 mid-edge-radii of the 24-cell.

The 24-cell can be constructed directly from its characteristic simplex , the irregular 5-cell which is the fundamental region of its symmetry group F₄, by reflection of that 4- orthoscheme in its own cells (which are 3-orthoschemes).

Relationships among interior polytopes

The 24-cell, three tesseracts, and three 16-cells are deeply entwined around their common center, and intersect in a common core. The tesseracts and the 16-cells are rotated 60° isoclinically with respect to each other. This means that the corresponding vertices of two tesseracts or two 16-cells are (120°) apart.

The tesseracts are inscribed in the 24-cell such that their vertices and edges are exterior elements of the 24-cell, but their square faces and cubical cells lie inside the 24-cell (they are not elements of the 24-cell). The 16-cells are inscribed in the 24-cell such that only their vertices are exterior elements of the 24-cell: their edges, triangular faces, and tetrahedral cells lie inside the 24-cell. The interior 16-cell edges have length .

The 16-cells are also inscribed in the tesseracts: their edges are the face diagonals of the tesseract, and their 8 vertices occupy every other vertex of the tesseract. Each tesseract has two 16-cells inscribed in it (occupying the opposite vertices and face diagonals), so each 16-cell is inscribed in two of the three 8-cells. This is reminiscent of the way, in 3 dimensions, two opposing regular tetrahedra can be inscribed in a cube, as discovered by Kepler. In fact it is the exact dimensional analogy (the demihypercubes), and the 48 tetrahedral cells are inscribed in the 24 cubical cells in just that way.

The 24-cell encloses the three tesseracts within its envelope of octahedral facets, leaving 4-dimensional space in some places between its envelope and each tesseract's envelope of cubes. Each tesseract encloses two of the three 16-cells, leaving 4-dimensional space in some places between its envelope and each 16-cell's envelope of tetrahedra. Thus there are measurable 4-dimensional interstices between the 24-cell, 8-cell and 16-cell envelopes. The shapes filling these gaps are 4-pyramids, alluded to above.

Boundary cells

Despite the 4-dimensional interstices between 24-cell, 8-cell and 16-cell envelopes, their 3-dimensional volumes overlap. The different envelopes are separated in some places, and in contact in other places (where no 4-pyramid lies between them). Where they are in contact, they merge and share cell volume: they are the same 3-membrane in those places, not two separate but adjacent 3-dimensional layers. Because there are a total of 7 envelopes, there are places where several envelopes come together and merge volume, and also places where envelopes interpenetrate (cross from inside to outside each other).

Some interior features lie within the 3-space of the (outer) boundary envelope of the 24-cell itself: each octahedral cell is bisected by three perpendicular squares (one from each of the tesseracts), and the diagonals of those squares (which cross each other perpendicularly at the center of the octahedron) are 16-cell edges (one from each 16-cell). Each square bisects an octahedron into two square pyramids, and also bonds two adjacent cubic cells of a tesseract together as their common face.

As we saw above, 16-cell tetrahedral cells are inscribed in tesseract cubic cells, sharing the same volume. 24-cell octahedral cells overlap their volume with cubic cells: they are bisected by a square face into two square pyramids, the apexes of which also lie at a vertex of a cube. The octahedra share volume not only with the cubes, but with the tetrahedra inscribed in them; thus the 24-cell, tesseracts, and 16-cells all share some boundary volume.

As a configuration

This configuration matrix represents the 24-cell. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers say how many of each element occur in the whole 24-cell. The non-diagonal numbers say how many of the column's element occur in or at the row's element.

$\begin\begin24 & 8 & 12 & 6 \\ 2 & 96 & 3 & 3 \\ 3 & 3 & 96 & 2 \\ 6 & 12 & 8 & 24 \end\end$

Since the 24-cell is self-dual, its matrix is identical to its 180 degree rotation.

Symmetries, root systems, and tessellations

The 24 root vectors of the D₄ root system of the simple Lie group SO(8) form the vertices of a 24-cell. The vertices can be seen in 3 hyperplanes, with the 6 vertices of an octahedron cell on each of the outer hyperplanes and 12 vertices of a cuboctahedron on a central hyperplane. These vertices, combined with the 8 vertices of the 16-cell, represent the 32 root vectors of the B₄ and C₄ simple Lie groups.

The 48 vertices (or strictly speaking their radius vectors) of the union of the 24-cell and its dual form the root system of type F₄. The 24 vertices of the original 24-cell form a root system of type D₄; its size has the ratio :1. This is likewise true for the 24 vertices of its dual. The full symmetry group of the 24-cell is the Weyl group of F₄, which is generated by reflections through the hyperplanes orthogonal to the F₄ roots. This is a solvable group of order 1152. The rotational symmetry group of the 24-cell is of order 576.

Quaternionic interpretation

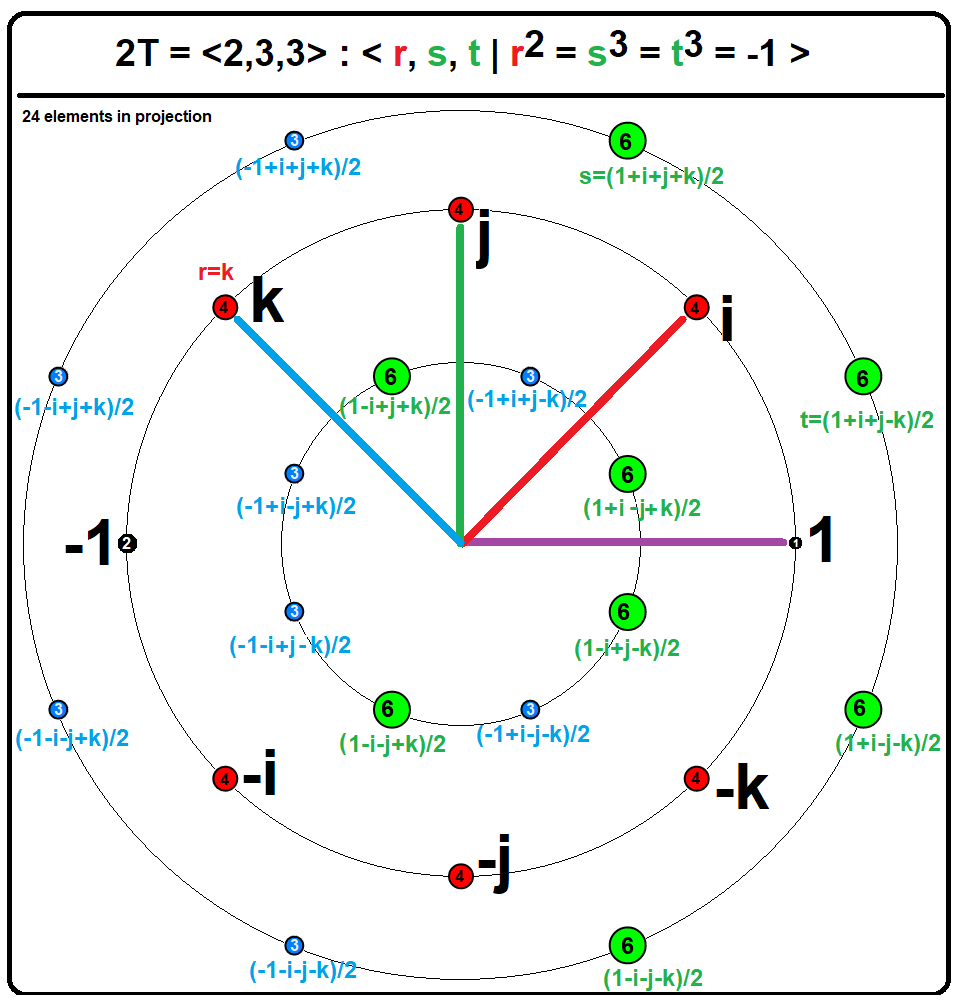When interpreted as the quaternions, the F₄ root lattice (which is the integral span of the vertices of the 24-cell) is closed under multiplication and is therefore a ring. This is the ring of Hurwitz integral quaternions. The vertices of the 24-cell form the group of units (i.e. the group of invertible elements) in the Hurwitz quaternion ring (this group is also known as the binary tetrahedral group). The vertices of the 24-cell are precisely the 24 Hurwitz quaternions with norm squared 1, and the vertices of the dual 24-cell are those with norm squared 2. The D₄ root lattice is the dual of the F₄ and is given by the subring of Hurwitz quaternions with even norm squared.

Viewed as the 24 unit Hurwitz quaternions, the unit radius coordinates of the 24-cell represent (in antipodal pairs) the 12 rotations of a regular tetrahedron.

Vertices of other convex regular 4-polytopes also form multiplicative groups of quaternions, but few of them generate a root lattice.

Voronoi cells

The Voronoi cells of the D₄ root lattice are regular 24-cells. The corresponding Voronoi tessellation gives the tessellation of 4-dimensional Euclidean space by regular 24-cells, the 24-cell honeycomb. The 24-cells are centered at the D₄ lattice points (Hurwitz quaternions with even norm squared) while the vertices are at the F₄ lattice points with odd norm squared. Each 24-cell of this tessellation has 24 neighbors. With each of these it shares an octahedron. It also has 24 other neighbors with which it shares only a single vertex. Eight 24-cells meet at any given vertex in this tessellation. The Schläfli symbol for this tessellation is . It is one of only three regular tessellations of R⁴.

The unit balls inscribed in the 24-cells of this tessellation give rise to the densest known lattice packing of hyperspheres in 4 dimensions. The vertex configuration of the 24-cell has also been shown to give the highest possible kissing number in 4 dimensions.

Radially equilateral honeycomb

The dual tessellation of the 24-cell honeycomb is the 16-cell honeycomb . The third regular tessellation of four dimensional space is the tesseractic honeycomb , whose vertices can be described by 4-integer Cartesian coordinates. The congruent relationships among these three tessellations can be helpful in visualizing the 24-cell, in particular the radial equilateral symmetry which it shares with the tesseract.

A honeycomb of unit edge length 24-cells may be overlaid on a honeycomb of unit edge length tesseracts such that every vertex of a tesseract (every 4-integer coordinate) is also the vertex of a 24-cell (and tesseract edges are also 24-cell edges), and every center of a 24-cell is also the center of a tesseract. The 24-cells are twice as large as the tesseracts by 4-dimensional content (hypervolume), so overall there are two tesseracts for every 24-cell, only half of which are inscribed in a 24-cell. If those tesseracts are colored black, and their adjacent tesseracts (with which they share a cubical facet) are colored red, a 4-dimensional checkerboard results. Of the 24 center-to-vertex radii of each 24-cell, 16 are also the radii of a black tesseract inscribed in the 24-cell. The other 8 radii extend outside the black tesseract (through the centers of its cubical facets) to the centers of the 8 adjacent red tesseracts. Thus the 24-cell honeycomb and the tesseractic honeycomb coincide in a special way: 8 of the 24 vertices of each 24-cell do not occur at a vertex of a tesseract (they occur at the center of a tesseract instead). Each black tesseract is cut from a 24-cell by truncating it at these 8 vertices, slicing off 8 cubic pyramids (as in reversing Gosset's construction, but instead of being removed the pyramids are simply colored red and left in place). Eight 24-cells meet at the center of each red tesseract: each one meets its opposite at that shared vertex, and the six others at a shared octahedral cell.

The red tesseracts are filled cells (they contain a central vertex and radii); the black tesseracts are empty cells. The vertex set of this union of two honeycombs includes the vertices of all the 24-cells and tesseracts, plus the centers of the red tesseracts. Adding the 24-cell centers (which are also the black tesseract centers) to this honeycomb yields a 16-cell honeycomb, the vertex set of which includes all the vertices and centers of all the 24-cells and tesseracts. The formerly empty centers of adjacent 24-cells become the opposite vertices of a unit edge length 16-cell. 24 half-16-cells (octahedral pyramids) meet at each formerly empty center to fill each 24-cell, and their octahedral bases are the 6-vertex octahedral facets of the 24-cell (shared with an adjacent 24-cell).

Notice the complete absence of pentagons anywhere in this union of three honeycombs. Like the 24-cell, 4-dimensional Euclidean space itself is entirely filled by a complex of all the polytopes that can be built out of regular triangles and squares (except the 5-cell), but that complex does not require (or permit) any of the pentagonal polytopes.

Rotations

The regular convex 4-polytopes are an expression of their underlying symmetry which is known as SO(4), the group of rotations about a fixed point in 4-dimensional Euclidean space.

The 3 Cartesian bases of the 24-cell

There are three distinct orientations of the tesseractic honeycomb which could be made to coincide with the 24-cell honeycomb, depending on which of the 24-cell's three disjoint sets of 8 orthogonal vertices (which set of 4 perpendicular axes, or equivalently, which inscribed basis 16-cell) was chosen to align it, just as three tesseracts can be inscribed in the 24-cell, rotated with respect to each other. The distance from one of these orientations to another is an isoclinic rotation through 60 degrees (a double rotation of 60 degrees in each pair of orthogonal invariant planes, around a single fixed point). This rotation can be seen most clearly in the hexagonal central planes, where the hexagon rotates to change which of its three diameters is aligned with a coordinate system axis.

Planes of rotation

Rotations in 4-dimensional Euclidean space can be seen as the composition of two 2-dimensional rotations in completely orthogonal planes. Thus the general rotation in 4-space is a ''double rotation''. There are two important special cases, called a ''simple rotation'' and an ''isoclinic rotation''.

Simple rotations

In 3 dimensions a spinning polyhedron has a single invariant central ''plane of rotation''. The plane is called ''invariant'' because each point in the plane moves in a circle but stays within the plane. Only ''one'' of a polyhedron's central planes can be invariant during a particular rotation; the choice of invariant central plane, and the angular distance it is rotated, completely specifies the rotation. Points outside the invariant plane also move in circles (unless they are on the fixed ''axis of rotation'' perpendicular to the invariant plane), but the circles do not lie within a ''central'' plane.

When a 4-polytope is rotating with only one invariant central plane, the same kind of simple rotation is happening that occurs in 3 dimensions. One difference is that instead of a fixed axis of rotation, there is an entire fixed central plane in which the points do not move. (Another difference is that there is more than one plane of rotation, because in four dimensions there is a set of central planes Clifford parallel to the invariant plane of rotation.) The fixed plane is the one central plane that is completely orthogonal to the invariant plane of rotation. In the 24-cell, there is a simple rotation which will take any vertex ''directly'' to any other vertex, also moving most of the other vertices but leaving at least 2 and at most 6 other vertices fixed (the vertices that the fixed central plane intersects). The vertex moves along a great circle in the invariant plane of rotation (and in its Clifford parallel planes) between adjacent vertices of a great hexagon, a great square or a great digon, and the completely orthogonal fixed plane is a digon, a square or a hexagon, respectively.

Double rotations

The points in the completely orthogonal central plane are not ''constrained'' to be fixed. It is also possible for them to be rotating in circles, as a second invariant plane, at a rate independent of the first invariant plane's rotation: a double rotation in two perpendicular non-intersecting planes of rotation at once. In a double rotation there is no fixed plane or axis: every point moves except the center point. The angular distance rotated may be different in the two completely orthogonal central planes, but they are always both invariant: their circularly moving points remain within the plane ''as the whole plane tilts sideways'' in the completely orthogonal rotation. A rotation in 4-space always has (at least) ''two'' completely orthogonal invariant planes of rotation, although in a simple rotation the angle of rotation in one of them is 0.

Double rotations come in two chiral forms: ''left'' and ''right'' rotations. In a double rotation each vertex moves in a spiral along two completely orthogonal great circles at once. Either the path is right-hand Screw thread#Handedness, threaded (like most screws and bolts), moving along the circles in the "same" directions, or it is left-hand threaded (like a reverse-threaded bolt), moving along the circles in what we conventionally say are "opposite" directions (according to the right hand rule by which we conventionally say which way is "up" on each of the 4 coordinate axes).

In double rotations of the 24-cell that take vertices to vertices, one invariant plane of rotation contains either a great hexagon, a great square, or only an axis (two vertices, a great digon). The completely orthogonal invariant plane of rotation will necessarily contain a great digon, a great square, or a great hexagon, respectively. The selection of an invariant plane of rotation, a rotational direction and angle through which to rotate it, and a rotational direction and angle through which to rotate its completely orthogonal plane, completely determines the nature of the rotational displacement. In the 24-cell there are several noteworthy kinds of double rotation permitted by these parameters.

Isoclinic rotations

When the angles of rotation in the two invariant planes are exactly the same, a Rotations in 4-dimensional Euclidean space#Special property of SO(4) among rotation groups in general, remarkably symmetric Geometric transformation, transformation occurs: all the great circle planes Clifford parallel to the invariant planes become invariant planes of rotation themselves, through that same angle, and the 4-polytope rotates Rotations in 4-dimensional Euclidean space#Isoclinic rotations, isoclinically in many directions at once. Each vertex moves an equal distance in four orthogonal directions at the same time. In the 24-cell any isoclinic rotation through 60 degrees in a hexagonal plane takes each vertex to a vertex two edge lengths away, rotates ''all 16'' hexagons by 60 degrees, and takes ''every'' great circle polygon (square, hexagon or triangle) to a Clifford parallel great circle polygon of the same kind 120 degrees away. An isoclinic rotation is also called a ''Clifford displacement'', after its William Kingdon Clifford, discoverer.

The 24-cell in the ''double'' rotation animation appears to turn itself inside out. It appears to, because it actually does, reversing the chirality of the whole 4-polytope just the way your bathroom mirror reverses the chirality of your image by a 180 degree reflection. Each 360 degree isoclinic rotation is as if the 24-cell surface had been stripped off like a glove and turned inside out, making a right-hand glove into a left-hand glove (or vice versa).

In a simple rotation of the 24-cell in a hexagonal plane, each vertex in the plane rotates first along an edge to an adjacent vertex 60 degrees away. But in an isoclinic rotation in ''two'' completely orthogonal planes one of which is a great hexagon, each vertex rotates first to a vertex ''two'' edge lengths away ( and 120° distant). The double 60-degree rotation's helical geodesics pass through every other vertex, missing the vertices in between. Each chord of the helical geodesic crosses between two Clifford parallel hexagon central planes, and lies in another hexagon central plane that intersects them both. The chords meet at a 60° angle, but since they lie in different planes they form a helix not a #Triangles, triangle. Three chords and 360° of rotation takes the vertex to an adjacent vertex, not back to itself. The helix of chords closes into a loop only after six chords: a 720° rotation twice around the 24-cell on a Skew polygon#Regular skew polygons in four dimensions, skew hexagram with edges. Even though all the vertices and all the hexagons rotate at once, a 360 degree isoclinic rotation hits only half the vertices in the 24-cell. After 360 degrees each helix has departed from 3 vertices and reached a fourth vertex adjacent to the original vertex, but has ''not'' arrived back exactly at the vertex it departed from. Each central plane (every hexagon or square in the 24-cell) has rotated 360 degrees ''and'' been tilted sideways all the way around 360 degrees back to its original position (like a coin flipping twice), but the 24-cell's Orientation entanglement, orientation in the 4-space in which it is embedded is now different. Because the 24-cell is now inside-out, if the isoclinic rotation is continued in the ''same'' direction through another 360 degrees, the moving vertices will pass through the other half of the vertices that were missed on the first revolution (the 12 antipodal vertices of the 12 that were hit the first time around), and each isoclinic geodesic ''will'' arrive back at the vertex it departed from, forming a closed six-chord helical loop. It takes a 720 degree isoclinic rotation for each #Helical hexagrams and their isoclines, hexagram₂ geodesic to complete a circuit through every ''second'' vertex of its six vertices by Winding number, winding around the 24-cell twice, returning the 24-cell to its original chiral orientation.

The hexagonal winding path that each vertex takes as it loops twice around the 24-cell forms a double helix bent into a Möbius strip, Möbius ring, so that the two strands of the double helix form a continuous single strand in a closed loop. In the first revolution the vertex traverses one 3-chord strand of the double helix; in the second revolution it traverses the second 3-chord strand, moving in the same rotational direction with the same handedness (bending either left or right) throughout. Although this isoclinic Möbius #6-cell rings, ring is a closed spiral not a 2-dimensional circle, like a great circle it is a geodesic because it is the shortest path from vertex to vertex in some rotation.

Clifford parallel polytopes

Two planes are also called ''isoclinic'' if an isoclinic rotation will bring them together. The isoclinic planes are precisely those central planes with Clifford parallel geodesic great circles. Clifford parallel great circles do not intersect, so isoclinic great circle polygons have disjoint vertices. In the 24-cell every hexagonal central plane is isoclinic to three others, and every square central plane is isoclinic to five others. We can pick out 4 mutually isoclinic (Clifford parallel) great hexagons (four different ways) covering all 24 vertices of the 24-cell just once (a hexagonal fibration). We can pick out 6 mutually isoclinic (Clifford parallel) great squares (three different ways) covering all 24 vertices of the 24-cell just once (a square fibration).

Two dimensional great circle polygons are not the only polytopes in the 24-cell which are parallel in the Clifford sense. Congruent polytopes of 2, 3 or 4 dimensions can be said to be Clifford parallel in 4 dimensions if their corresponding vertices are all the same distance apart. The three 16-cells inscribed in the 24-cell are Clifford parallels. Clifford parallel polytopes are ''completely disjoint'' polytopes. A 60 degree isoclinic rotation in hexagonal planes takes each 16-cell to a disjoint 16-cell. Like all #Double rotations, double rotations, isoclinic rotations come in two chiral forms: there is a disjoint 16-cell to the ''left'' of each 16-cell, and another to its ''right''.

All Clifford parallel 4-polytopes are related by an isoclinic rotation, but not all isoclinic polytopes are Clifford parallels (completely disjoint). The three 8-cells in the 24-cell are isoclinic but not Clifford parallel. Like the 16-cells, they are rotated 60 degrees isoclinically with respect to each other, but their vertices are not all disjoint (and therefore not all equidistant). Each vertex occurs in two of the three 8-cells (as each 16-cell occurs in two of the three 8-cells).

Isoclinic rotations relate the convex regular 4-polytopes to each other. An isoclinic rotation of a single 16-cell will generate a 24-cell. A simple rotation of a single 16-cell will not, because its vertices will not reach either of the other two 16-cells' vertices in the course of the rotation. An isoclinic rotation of the 24-cell will generate the 600-cell, and an isoclinic rotation of the 600-cell will generate the 120-cell. (Or they can all be generated directly by an isoclinic rotation of the 16-cell, generating isoclinic copies of itself.) The convex regular 4-polytopes nest inside each other, and hide next to each other in the Clifford parallel spaces that comprise the 3-sphere. For an object of more than one dimension, the only way to reach these parallel subspaces directly is by isoclinic rotation.

Rings

In the 24-cell there are sets of rings of six different kinds, described separately in detail in other sections of this article. This section describes how the different kinds of rings are #Relationships among interior polytopes, intertwined.

The 24-cell contains four kinds of #Geodesics, geodesic fibers (polygonal rings running through vertices): #Squares, great circle squares and their 16-cell#Helical construction, isoclinic helix octagrams, and #Hexagons, great circle hexagons and their #Isoclinic rotations, isoclinic helix hexagrams. It also contains two kinds of #Cell rings, cell rings (chains of octahedra bent into a ring in the fourth dimension): four octahedra connected vertex-to-vertex and bent into a square, and six octahedra connected face-to-face and bent into a hexagon.

4-cell rings

Four unit-edge-length octahedra can be connected vertex-to-vertex along a common axis of length 4. The axis can then be bent into a square of edge length . Although it is possible to do this in a space of only three dimensions, that is not how it occurs in the 24-cell. Although the axes of the four octahedra occupy the same plane, forming one of the 18 great squares of the 24-cell, each octahedron occupies a different 3-dimensional hyperplane, and all four dimensions are utilized. The 24-cell can be partitioned into 6 such 4-cell rings (three different ways), mutually interlinked like adjacent links in a chain (but these Link (knot theory), links all have a common center). A #Simple rotations, simple rotation in the great square plane by a multiple of 90° takes each octahedron in the ring to an octahedron in the ring.

6-cell rings

Six regular octahedra can be connected face-to-face along a common axis that passes through their centers of volume, forming a stack or column with only triangular faces. In a space of four dimensions, the axis can then be bent 60° in the fourth dimension at each of the six octahedron centers, in a plane orthogonal to all three orthogonal central planes of each octahedron, such that the top and bottom triangular faces of the column become coincident. The column becomes a ring around a hexagonal axis. The 24-cell can be partitioned into 4 such rings (four different ways), mutually interlinked. Because the hexagonal axis joins cell centers (not vertices), it is not a great hexagon of the 24-cell. However, six great hexagons can be found in the ring of six octahedra, running along the edges of the octahedra. In the column of six octahedra (before it is bent into a ring) there are six spiral paths along edges running up the column: three parallel helices spiraling clockwise, and three parallel helices spiraling counterclockwise. Each clockwise helix intersects each counterclockwise helix at two vertices three edge lengths apart. Bending the column into a ring changes these helices into great circle hexagons. The ring has two sets of three great hexagons, each on three Clifford parallel great circles. The great hexagons in each parallel set of three do not intersect, but each intersects the other three great hexagons (to which it is not Clifford parallel) at two antipodal vertices. A #Simple rotations, simple rotation in any of the great hexagon planes by a multiple of 60° rotates all three parallel great hexagon planes similarly, and takes each octahedron in the ring to an octahedron in the ring.

Helical hexagrams and their isoclines

Another kind of geodesic fiber, the #Isoclinic rotations, isoclinic helix hexagrams, can be found within a 6-cell ring of octahedra. Each of these geodesics runs through every ''second'' vertex of a skew hexagram₂, which in the unit-radius, unit-edge-length 24-cell has six edges. It does not lie in a single central plane, but is composed of six linked chords from six different hexagonal great circles. This geodesic fiber is the path of an isoclinic rotation, a helical rather than simply circular path around the 24-cell which links vertices two edge lengths apart and consequently must wrap twice around the 24-cell before completing its six-vertex loop. Rather than a flat hexagon, it forms a skew polygon, skew hexagram out of two three-sided 360 degree half-loops: open triangles joined end-to-end to each other in a six-sided Möbius loop. An isoclinic rotation in any of the great hexagon planes by 60° rotates all ''six'' great hexagon planes by 60°, and takes each octahedron in the ring to a ''non-adjacent'' octahedron in the ring. Each isoclinically displaced octahedron is itself rotated isoclinically. After a 360° isoclinic rotation each octahedron is back in the same position, but in a different orientation. In a 720° isoclinic rotation, its vertices are returned to their original Orientation entanglement, orientation.

Each 6-cell ring contains six such isoclinic skew hexagrams, three left-handed and three right-handed, each left-right pair belonging to a different Hopf fibration, fibration of hexagrams. Beginning at any vertex at one end of the column of six octahedra, we can follow an isoclinic path of chords from octahedron to octahedron. In the 24-cell the edges are #Hexagons, great hexagon edges (and octahedron edges); in the column of six octahedra we see six great hexagons running along the octahedra's edges. The chords are great hexagon diagonals, joining great hexagon vertices two edges apart. We find them in the ring of six octahedra running from a vertex in one octahedron to a vertex in the next octahedron, passing through the face shared by the two octahedra (but not touching any of the face's 3 vertices). Each chord is a chord of just one great hexagon (an edge of a #Triangles, great triangle inscribed in that great hexagon), but successive chords belong to different great hexagons. At each vertex the isoclinic path of chords bends 60 degrees in two completely orthogonal central planes at once: 60 degrees around the great hexagon that the chord before the vertex belongs to, and 60 degrees into the plane of a different great hexagon entirely, that the chord after the vertex belongs to. Thus the path follows one great hexagon from each octahedron to the next, but switches to another of the six great hexagons in the next link of the hexagram₂ path. Followed along the column of six octahedra (and "around the end" where the column is bent into a ring) the path may at first appear to be zig-zagging between two hexagonal central planes (like a Petrie polygon), but it is not: any isoclinic path we can pick out always bends either right or left, never changing its inherent chiral "direction", as it visits all six of the great hexagons in the 6-cell ring. When it has traversed one chord from each of the six great hexagons, after 720 degrees of isoclinic rotation (either left or right), it closes its skew hexagram and begins to repeat itself (still bending in the same direction).

At each vertex, there are four great hexagons and four hexagram isoclines (all four either left-handed right-handed) that cross at the vertex and share a 24-cell axis chord. Each left-right pair at the axis is Clifford parallel and belongs to one of four different fibrations of the hexagram isoclines. Four left-right pairs of isoclines together (one pair at each axis) visit all 24 vertices and comprise a discrete fibration of the 24-cell's 60° isoclines (just as four great hexagons together, one at each axis, comprise a discrete fibration of the 24-cell's 60° great circles).

Helical octagrams and their isoclines

Eighteen isoclinic helix octagrams (nine left-handed and nine right-handed) can be found within the six orthogonal #4-cell rings, 4-cell rings of octahedra. (Each 4-cell ring has cells bonded vertex-to-vertex around a great square axis). Three left-right pairs of octagram edge-helices are found in each of the three inscribed 16-cells, described elsewhere as the 16-cell#Helical construction, helical construction of the 16-cell. In summary, each 16-cell consists of a left-right pair of 8-cell rings of -edged tetrahedral cells. Each 8-cell ring is bounded by three intersecting octagram edge-helices which twist around a common isocline axis that circles through all eight vertices. The chords of the isoclines connect opposite vertices of face-bonded tetrahedral cells, which are also opposite vertices (antipodal vertices) of the 16-cell, so they are chords.

In the 24-cell's 4-cell ring of octahedra with a great square axis, we find antipodal vertices at opposite vertices of the great square. A chord (the diagonal of the great square) connects them; this is a chord of two octagram isoclines (one left-handed and one right-handed). #Boundary cells, Boundary cells describes how the axes of the 24-cell's octahedral cells are the edges of the 16-cell's tetrahedral cells, each tetrahedron is inscribed in a (tesseract) cube, and each octahedron is inscribed in a pair of cubes (from different tesseracts), bridging them. The vertex-bonded octahedra of the 4-cell ring also lie in different tesseracts. In the 24-cell, the 16-cells' isoclines' chords describe an Octagram#Star polygon compounds, octagram₄ with edges that run from the vertex of one cube and octahedron and tetrahedron, to the vertex of another cube and octahedron and tetrahedron (in a different tesseract), straight through the center of the 24-cell on one of the twelve axes.

The octahedra in the 4-cell rings are vertex-bonded to more than two other octahedra, because three 4-cell rings (and their three axial great squares, which belong to different 16-cells) cross at 90° at each bonding vertex. At that vertex the octagram makes two right-angled turns at once: 90° around the great square, and 90° completely orthogonally into a different 4-cell ring entirely. The 180° arc of each chord of the octagram runs through the volumes and opposite vertices of two face-bonded tetrahedra (in the same 16-cell), which are also the opposite vertices of two vertex-bonded octahedra in different 4-cell rings (and different tesseracts). The arc does not hit any vertices of those two octahedra except the chord endpoints; in particular, it misses the vertex near the chord midpoint where the two octahedra are vertex-bonded. The octagram, 720° octagram isocline runs through ''one'' vertex of ''one'' octahedron in eight different 4-cell rings (of the 18 4-cell rings in the 24-cell), and through the volumes of 16 tetrahedra. At each vertex, there are three great squares and two octagram isoclines (a left and a right) that cross at the vertex and share a 24-cell axis chord.

Characteristic orthoscheme

Every regular 4-polytope has its Orthoscheme#Characteristic simplex of the general regular polytope, characteristic 4-orthoscheme, an irregular 5-cell. The characteristic 5-cell of the regular 24-cell is represented by the Coxeter-Dynkin diagram , which can be read as a list of the dihedral angles between its mirror facets. It is an irregular Pyramid (mathematics)#Polyhedral pyramid, tetrahedral pyramid based on the Octahedron#Characteristic orthoscheme, characteristic tetrahedron of the regular octahedron. The regular 24-cell is subdivided by its symmetry hyperplanes into 1152 instances of its characteristic 5-cell that all meet at its center.

The characteristic 5-cell (4-orthoscheme) has four more edges than its base characteristic tetrahedron (3-orthoscheme), joining the four vertices of the base to its apex (the fifth vertex of the 4-orthoscheme, at the center of the regular 24-cell). If the regular 24-cell has radius and edge length 𝒍 = 1, its characteristic 5-cell's ten edges have lengths $\sqrt$, $\sqrt$, $\sqrt$ (the exterior right triangle face, the ''characteristic triangle'' 𝟀, 𝝓, 𝟁), plus $\sqrt$, $\sqrt$, $\sqrt$ (the other three edges of the exterior 3-orthoscheme facet the characteristic tetrahedron, which are the ''characteristic radii'' of the octahedron), plus $1$, $\sqrt$, $\sqrt$, $\sqrt$ (edges which are the characteristic radii of the 24-cell). The 4-edge path along orthogonal edges of the orthoscheme is $\sqrt$, $\sqrt$, $\sqrt$, $\sqrt$, first from a 24-cell vertex to a 24-cell edge center, then turning 90° to a 24-cell face center, then turning 90° to a 24-cell octahedral cell center, then turning 90° to the 24-cell center.

Reflections

The 24-cell can be #Tetrahedral constructions, constructed by the reflections of its characteristic 5-cell in its own facets (its tetrahedral mirror walls). Reflections and rotations are related: a reflection in an ''even'' number of ''intersecting'' mirrors is a rotation. Consequently, regular polytopes can be generated by reflections or by rotations. For example, any #Isoclinic rotations, 720° isoclinic rotation of the 24-cell in a hexagonal invariant plane takes ''each'' of the 24 vertices to and through 5 other vertices and back to itself, on a skew #Helical hexagrams and their isoclines, hexagram₂ geodesic isocline that winds twice around the 3-sphere on every ''second'' vertex of the hexagram. Any set of #The 3 Cartesian bases of the 24-cell, four orthogonal pairs of antipodal vertices (the 8 vertices of one of the #Relationships among interior polytopes, three inscribed 16-cells) performing ''half'' such an orbit visits 3 * 8 = 24 distinct vertices and #Clifford parallel polytopes, generates the 24-cell sequentially in 3 steps of a single 360° isoclinic rotation, just as any single characteristic 5-cell reflecting itself in its own mirror walls generates the 24 vertices simultaneously by reflection.

Tracing the orbit of ''one'' such 16-cell vertex during the 360° isoclinic rotation reveals more about the relationship between reflections and rotations as generative operations. The vertex follows an #Helical hexagrams and their isoclines, isocline (a doubly curved geodesic circle) rather than any one of the singly curved geodesic circles that are the great circle segments over each chord of the rotation. The isocline connects vertices two edge lengths apart, but curves away from the great circle path over the two edges connecting those vertices, missing the vertex in between. Although the isocline does not follow any one great circle, it is contained within a ring of another kind: in the 24-cell it stays within a #6-cell rings, 6-cell ring of spherical octahedral cells, intersecting one vertex in each cell, and passing through the volume of two adjacent cells near the missed vertex.

Visualization

Cell rings

The 24-cell is bounded by 24 octahedral cells. For visualization purposes, it is convenient that the octahedron has opposing parallel Face (geometry), faces (a trait it shares with the cells of the tesseract and the 120-cell). One can stack octahedrons face to face in a straight line bent in the 4th direction into a great circle with a circumference of 6 cells. The cell locations lend themselves to a 3-sphere, hyperspherical description. Pick an arbitrary cell and label it the "North Pole". Eight great circle meridians (two cells long) radiate out in 3 dimensions, converging at the 3rd "South Pole" cell. This skeleton accounts for 18 of the 24 cells (2 + ). See the table below.

There is another related #Geodesics, great circle in the 24-cell, the dual of the one above. A path that traverses 6 vertices solely along edges resides in the dual of this polytope, which is itself since it is self dual. These are the #Hexagons, hexagonal geodesics #Geodesics, described above. One can easily follow this path in a rendering of the equatorial cuboctahedron cross-section.

Starting at the North Pole, we can build up the 24-cell in 5 latitudinal layers. With the exception of the poles, each layer represents a separate 2-sphere, with the equator being a great 2-sphere. The cells labeled equatorial in the following table are interstitial to the meridian great circle cells. The interstitial "equatorial" cells touch the meridian cells at their faces. They touch each other, and the pole cells at their vertices. This latter subset of eight non-meridian and pole cells has the same relative position to each other as the cells in a tesseract (8-cell), although they touch at their vertices instead of their faces.

The 24-cell can be partitioned into cell-disjoint sets of four of these 6-cell great circle rings, forming a discrete Hopf fibration of four interlocking rings. One ring is "vertical", encompassing the pole cells and four meridian cells. The other three rings each encompass two equatorial cells and four meridian cells, two from the northern hemisphere and two from the southern.

Note this hexagon great circle path implies the interior/dihedral angle between adjacent cells is 180 - 360/6 = 120 degrees. This suggests you can adjacently stack exactly three 24-cells in a plane and form a 4-D honeycomb of 24-cells as described previously.

One can also follow a #Geodesics, great circle route, through the octahedrons' opposing vertices, that is four cells long. These are the #Squares, square geodesics along four chords #Geodesics, described above. This path corresponds to traversing diagonally through the squares in the cuboctahedron cross-section. The 24-cell is the only regular polytope in more than two dimensions where you can traverse a great circle purely through opposing vertices (and the interior) of each cell. This great circle is self dual. This path was touched on above regarding the set of 8 non-meridian (equatorial) and pole cells.

The 24-cell can be equipartitioned into three 8-cell subsets, each having the organization of a tesseract. Each of these subsets can be further equipartitioned into two interlocking great circle chains, four cells long. Collectively these three subsets now produce another, six ring, discrete Hopf fibration.

Parallel projections

The ''vertex-first'' parallel projection of the 24-cell into 3-dimensional space has a rhombic dodecahedron, rhombic dodecahedral Projection envelope, envelope. Twelve of the 24 octahedral cells project in pairs onto six square dipyramids that meet at the center of the rhombic dodecahedron. The remaining 12 octahedral cells project onto the 12 rhombic faces of the rhombic dodecahedron.

The ''cell-first'' parallel projection of the 24-cell into 3-dimensional space has a cuboctahedron, cuboctahedral envelope. Two of the octahedral cells, the nearest and farther from the viewer along the ''w''-axis, project onto an octahedron whose vertices lie at the center of the cuboctahedron's square faces. Surrounding this central octahedron lie the projections of 16 other cells, having 8 pairs that each project to one of the 8 volumes lying between a triangular face of the central octahedron and the closest triangular face of the cuboctahedron. The remaining 6 cells project onto the square faces of the cuboctahedron. This corresponds with the decomposition of the cuboctahedron into a regular octahedron and 8 irregular but equal octahedra, each of which is in the shape of the convex hull of a cube with two opposite vertices removed.

The ''edge-first'' parallel projection has an elongated hexagonal dipyramidal envelope, and the ''face-first'' parallel projection has a nonuniform hexagonal bi-hexagonal antiprism, antiprismic envelope.

Perspective projections

The ''vertex-first'' perspective projection of the 24-cell into 3-dimensional space has a tetrakis hexahedron, tetrakis hexahedral envelope. The layout of cells in this image is similar to the image under parallel projection.

The following sequence of images shows the structure of the cell-first perspective projection of the 24-cell into 3 dimensions. The 4D viewpoint is placed at a distance of five times the vertex-center radius of the 24-cell.

Related polytopes

Three Coxeter group constructions

There are two lower symmetry forms of the 24-cell, derived as a ''Rectification (geometry), rectified 16-cell'', with B₄ or [3,3,4] symmetry drawn bicolored with 8 and 16 octahedral cells. Lastly it can be constructed from D₄ or [3^1,1,1] symmetry, and drawn tricolored with 8 octahedra each.

Related complex polygons

The regular complex polygon ₄₄, or contains the 24 vertices of the 24-cell, and 24 4-edges that correspond to central squares of 24 of 48 octahedral cells. Its symmetry is ₄[3]₄, order 96.

The regular complex polytope ₃₃, or , in $\mathbb^2$ has a real representation as a 24-cell in 4-dimensional space. ₃₃ has 24 vertices, and 24 3-edges. Its symmetry is ₃[4]₃, order 72.

Related 4-polytopes

Several uniform 4-polytopes can be derived from the 24-cell via Truncation (geometry), truncation:
* truncating at 1/3 of the edge length yields the truncated 24-cell;
* truncating at 1/2 of the edge length yields the rectified 24-cell;
* and truncating at half the depth to the dual 24-cell yields the bitruncated 24-cell, which is cell-transitive.

The 96 edges of the 24-cell can be partitioned into the golden ratio to produce the 96 vertices of the snub 24-cell. This is done by first placing vectors along the 24-cell's edges such that each two-dimensional face is bounded by a cycle, then similarly partitioning each edge into the golden ratio along the direction of its vector. An analogous modification to an octahedron produces an Regular icosahedron, icosahedron, or "Regular icosahedron#Uniform colorings and subsymmetries, snub octahedron."

The 24-cell is the unique convex self-dual regular Euclidean polytope that is neither a polygon nor a simplex (geometry), simplex. Relaxing the condition of convexity admits two further figures: the great 120-cell and grand stellated 120-cell. With itself, it can form a polytope compound: the #Symmetries, root systems, and tessellations, compound of two 24-cells.

Related uniform polytopes

The 24-cell can also be derived as a rectified 16-cell:

See also

*Octacube (sculpture)
*Uniform 4-polytope#The F4 family

Notes

Citations

References

*
*
*
*
** (Paper 3) H.S.M. Coxeter, ''Two aspects of the regular 24-cell in four dimensions''
** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', [Math. Zeit. 46 (1940) 380-407, MR 2,10]
** (Paper 23) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes II'', [Math. Zeit. 188 (1985) 559-591]
** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', [Math. Zeit. 200 (1988) 3-45]
*
*
*
*
*
*
* (also under Icositetrachoron)
*
*
*
*
*
*
*
*
*
*
*

External links

24-cell animations

{{Authority control

4-polytopes, 024
Articles containing video clips