|
Binary Tetrahedral Group
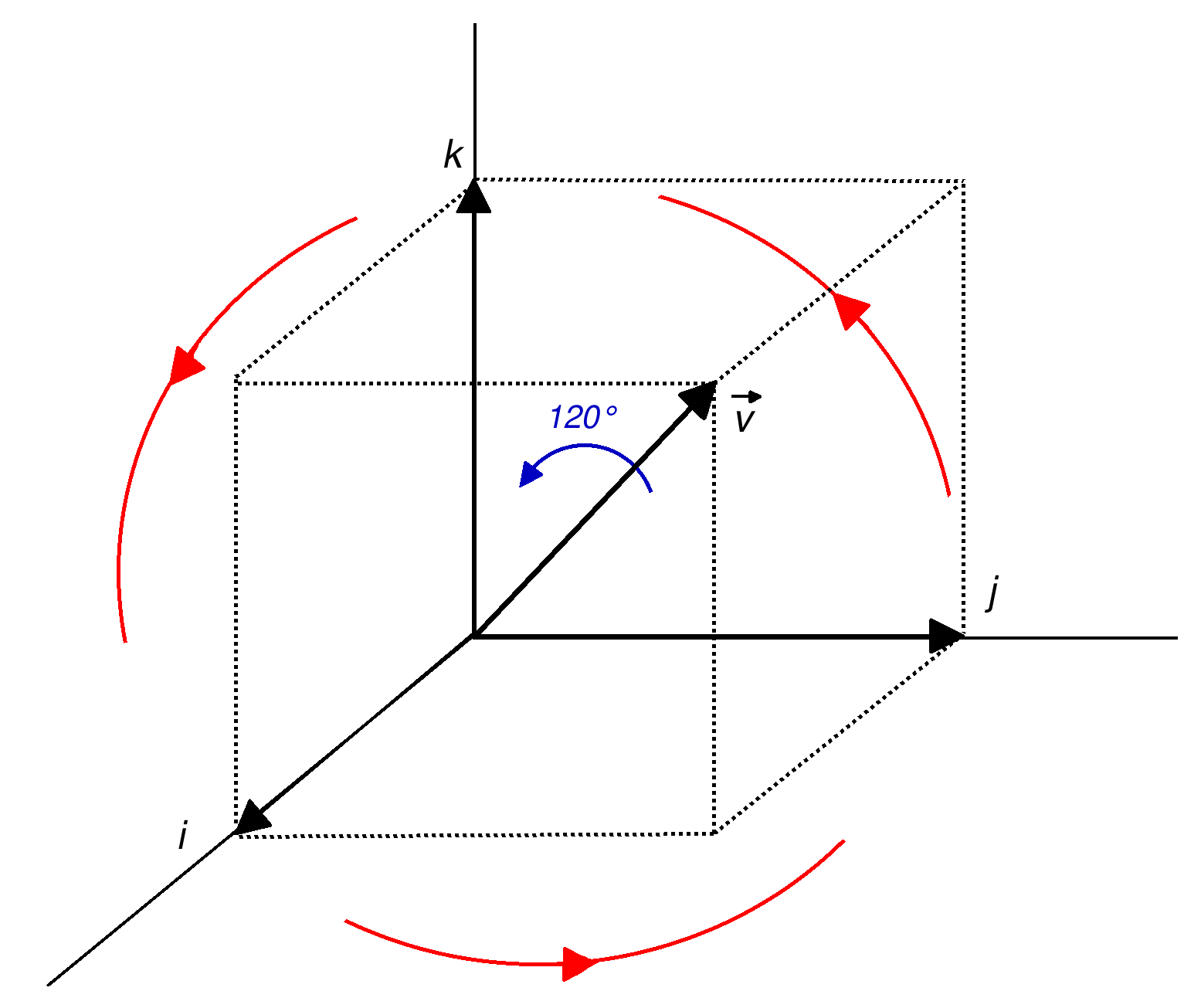
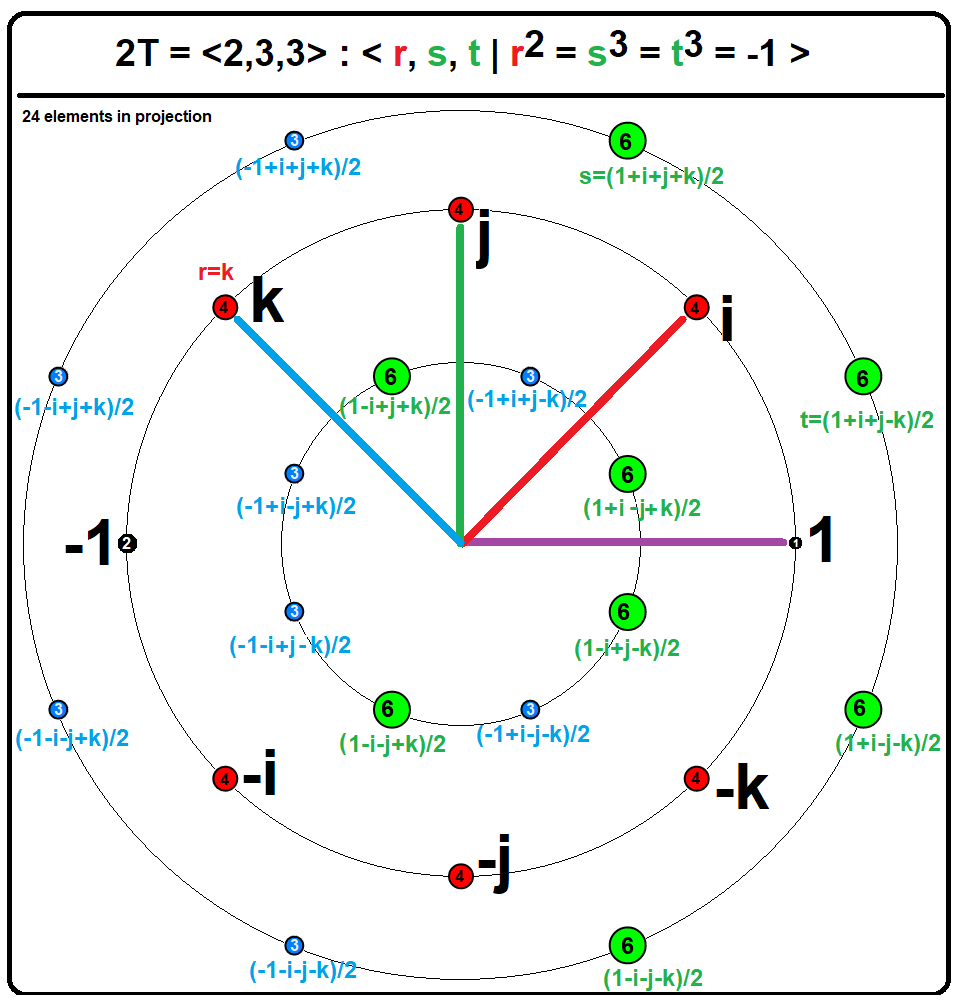
In mathematics, the binary tetrahedral group, denoted 2T or , Coxeter&Moser: Generators and Relations for discrete groups: : Rl = Sm = Tn = RST is a certain nonabelian group of order 24. It is an extension of the tetrahedral group T or (2,3,3) of order 12 by a cyclic group of order 2, and is the preimage of the tetrahedral group under the 2:1 covering homomorphism Spin(3) → SO(3) of the special orthogonal group by the spin group. It follows that the binary tetrahedral group is a discrete subgroup of Spin(3) of order 24. The complex reflection group named 3(24)3 by G.C. Shephard or 3 and by Coxeter, is isomorphic to the binary tetrahedral group. The binary tetrahedral group is most easily described concretely as a discrete subgroup of the unit quaternions, under the isomorphism , where Sp(1) is the multiplicative group of unit quaternions. (For a description of this homomorphism see the article on quaternions and spatial rotations.) Elements Expl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Polygon 3-6-2
Complex commonly refers to: * Complexity, the behaviour of a system whose components interact in multiple ways so possible interactions are difficult to describe ** Complex system, a system composed of many components which may interact with each other * Complex (psychology), a core pattern of emotions etc. in the personal unconscious organized around a common theme such as power or status Complex may also refer to: Arts, entertainment and media * Complex (English band), formed in 1968, and their 1971 album ''Complex'' * Complex (band), a Japanese rock band * ''Complex'' (album), by Montaigne, 2019, and its title track * ''Complex'' (EP), by Rifle Sport, 1985 * "Complex" (song), by Gary Numan, 1979 * Complex Networks, publisher of magazine ''Complex'', now online Biology * Protein–ligand complex, a complex of a protein bound with a ligand * Exosome complex, a multi-protein intracellular complex * Protein complex, a group of two or more associated polypeptide chains * Speci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quaternions And Spatial Rotation
unit vector, Unit quaternions, known as versor, ''versors'', provide a convenient mathematics, mathematical notation for representing spatial Orientation (geometry), orientations and rotations of elements in three dimensional space. Specifically, they encode information about an Axis–angle representation, axis-angle rotation about an arbitrary axis. Rotation and orientation quaternions have applications in computer graphics, Presented at SIGGRAPH '85. computer vision, robotics, navigation, molecular dynamics, flight dynamics, orbital mechanics of satellites, and Texture (crystalline), crystallographic texture analysis. When used to represent rotation, unit quaternions are also called rotation quaternions as they represent the 3D rotation group. When used to represent an Orientation (geometry), orientation (rotation relative to a reference coordinate system), they are called orientation quaternions or attitude quaternions. A spatial rotation around a fixed point of \theta radians ab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covering Groups Of The Alternating And Symmetric Groups
In the mathematical area of group theory, the covering groups of the alternating and symmetric groups are groups that are used to understand the projective representations of the alternating and symmetric groups. The covering groups were classified in : for , the covering groups are 2-fold covers except for the alternating groups of degree 6 and 7 where the covers are 6-fold. For example the binary icosahedral group covers the icosahedral group, an alternating group of degree 5, and the binary tetrahedral group covers the tetrahedral group, an alternating group of degree 4. Definition and classification A group homomorphism from ''D'' to ''G'' is said to be a Schur cover of the finite group ''G'' if: # the kernel is contained both in the center and the commutator subgroup of ''D'', and # amongst all such homomorphisms, this ''D'' has maximal size. The Schur multiplier of ''G'' is the kernel of any Schur cover and has many interpretations. When the homomorphism is understood, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semidirect Product
In mathematics, specifically in group theory, the concept of a semidirect product is a generalization of a direct product. There are two closely related concepts of semidirect product: * an ''inner'' semidirect product is a particular way in which a group can be made up of two subgroups, one of which is a normal subgroup. * an ''outer'' semidirect product is a way to construct a new group from two given groups by using the Cartesian product as a set and a particular multiplication operation. As with direct products, there is a natural equivalence between inner and outer semidirect products, and both are commonly referred to simply as ''semidirect products''. For finite groups, the Schur–Zassenhaus theorem provides a sufficient condition for the existence of a decomposition as a semidirect product (also known as splitting extension). Inner semidirect product definitions Given a group with identity element , a subgroup , and a normal subgroup , the following stateme ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Split Exact Sequence
In mathematics, a split exact sequence is a short exact sequence in which the middle term is built out of the two outer terms in the simplest possible way. Equivalent characterizations A short exact sequence of abelian groups or of modules over a fixed ring, or more generally of objects in an abelian category :0 \to A \mathrel B \mathrel C \to 0 is called split exact if it is isomorphic to the exact sequence where the middle term is the direct sum of the outer ones: :0 \to A \mathrel A \oplus C \mathrel C \to 0 The requirement that the sequence is isomorphic means that there is an isomorphism f : B \to A \oplus C such that the composite f \circ a is the natural inclusion i: A \to A \oplus C and such that the composite p \circ f equals ''b''. This can be summarized by a commutative diagram as: The splitting lemma provides further equivalent characterizations of split exact sequences. Examples A trivial example of a split short exact sequence is :0 \to M_1 \mathrel M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Short Exact Sequence
An exact sequence is a sequence of morphisms between objects (for example, groups, rings, modules, and, more generally, objects of an abelian category) such that the image of one morphism equals the kernel of the next. Definition In the context of group theory, a sequence :G_0\;\xrightarrow\; G_1 \;\xrightarrow\; G_2 \;\xrightarrow\; \cdots \;\xrightarrow\; G_n of groups and group homomorphisms is said to be exact at G_i if \operatorname(f_i)=\ker(f_). The sequence is called exact if it is exact at each G_i for all 1\leq i |
24-cell
In geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, octacube, hyper-diamond or polyoctahedron, being constructed of octahedral cells. The boundary of the 24-cell is composed of 24 octahedral cells with six meeting at each vertex, and three at each edge. Together they have 96 triangular faces, 96 edges, and 24 vertices. The vertex figure is a cube. The 24-cell is self-dual. It and the tesseract are the only convex regular 4-polytopes in which the edge length equals the radius. The 24-cell does not have a regular analogue in 3 dimensions. It is the only one of the six convex regular 4-polytopes which is not the four-dimensional analogue of one of the five regular Platonic solids. However, it can be seen as the analogue of a pair of irregular solids: the cuboctahedron and its dual the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Regular 4-polytope
In mathematics, a regular 4-polytope is a regular four-dimensional polytope. They are the four-dimensional analogues of the regular polyhedra in three dimensions and the regular polygons in two dimensions. There are six convex and ten star regular 4-polytopes, giving a total of sixteen. History The convex regular 4-polytopes were first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century. He discovered that there are precisely six such figures. Schläfli also found four of the regular star 4-polytopes: the grand 120-cell, great stellated 120-cell, grand 600-cell, and great grand stellated 120-cell. He skipped the remaining six because he would not allow forms that failed the Euler characteristic on cells or vertex figures (for zero-hole tori: ''F'' − ''E'' + ''V'' 2). That excludes cells and vertex figures such as the great dodecahedron and small stellated dodecahedron . Edmund Hess (1843–1903) publi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Hull
In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset. Convex hulls of open sets are open, and convex hulls of compact sets are compact. Every compact convex set is the convex hull of its extreme points. The convex hull operator is an example of a closure operator, and every antimatroid can be represented by applying this closure operator to finite sets of points. The algorithmic problems of finding the convex hull of a finite set of points in the plane or other low-dimensional Euclidean spaces, and its dual problem of intersecting half-spaces, are fundamental problems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hurwitz Integer
In mathematics, a Hurwitz quaternion (or Hurwitz integer) is a quaternion whose components are ''either'' all integers ''or'' all half-integers (halves of odd integers; a mixture of integers and half-integers is excluded). The set of all Hurwitz quaternions is :H = \left\. That is, either ''a'', ''b'', ''c'', ''d'' are all integers, or they are all half-integers. ''H'' is closed under quaternion multiplication and addition, which makes it a subring of the ring of all quaternions H. Hurwitz quaternions were introduced by . A Lipschitz quaternion (or Lipschitz integer) is a quaternion whose components are all integers. The set of all Lipschitz quaternions :L = \left\ forms a subring of the Hurwitz quaternions ''H''. Hurwitz integers have the advantage over Lipschitz integers that it is possible to perform Euclidean division on them, obtaining a small remainder. Both the Hurwitz and Lipschitz quaternions are examples of noncommutative domains which are not division rings. Stru ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ring (mathematics)
In mathematics, rings are algebraic structures that generalize fields: multiplication need not be commutative and multiplicative inverses need not exist. In other words, a ''ring'' is a set equipped with two binary operations satisfying properties analogous to those of addition and multiplication of integers. Ring elements may be numbers such as integers or complex numbers, but they may also be non-numerical objects such as polynomials, square matrices, functions, and power series. Formally, a ''ring'' is an abelian group whose operation is called ''addition'', with a second binary operation called ''multiplication'' that is associative, is distributive over the addition operation, and has a multiplicative identity element. (Some authors use the term " " with a missing i to refer to the more general structure that omits this last requirement; see .) Whether a ring is commutative (that is, whether the order in which two elements are multiplied might change the resu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Of Units
In algebra, a unit of a ring is an invertible element for the multiplication of the ring. That is, an element of a ring is a unit if there exists in such that vu = uv = 1, where is the multiplicative identity; the element is unique for this property and is called the multiplicative inverse of . The set of units of forms a group under multiplication, called the group of units or unit group of . Other notations for the unit group are , , and (from the German term ). Less commonly, the term ''unit'' is sometimes used to refer to the element of the ring, in expressions like ''ring with a unit'' or ''unit ring'', and also unit matrix. Because of this ambiguity, is more commonly called the "unity" or the "identity" of the ring, and the phrases "ring with unity" or a "ring with identity" may be used to emphasize that one is considering a ring instead of a rng. Examples The multiplicative identity and its additive inverse are always units. More generally, any root o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |