In
music theory
Music theory is the study of the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory". The first is the "rudiments", that are needed to understand music notation (ke ...
, an interval is a difference in
pitch between two sounds.
An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a
chord.
In
Western
Western may refer to:
Places
*Western, Nebraska, a village in the US
*Western, New York, a town in the US
*Western Creek, Tasmania, a locality in Australia
*Western Junction, Tasmania, a locality in Australia
*Western world, countries that id ...
music, intervals are most commonly differences between
notes
Note, notes, or NOTE may refer to:
Music and entertainment
* Musical note, a pitched sound (or a symbol for a sound) in music
* Notes (album), ''Notes'' (album), a 1987 album by Paul Bley and Paul Motian
* ''Notes'', a common (yet unofficial) sho ...
of a
diatonic scale
In music theory, a diatonic scale is any heptatonic scale that includes five whole steps (whole tones) and two half steps (semitones) in each octave, in which the two half steps are separated from each other by either two or three whole steps, ...
. Intervals between successive notes of a scale are also known as scale steps. The smallest of these intervals is a
semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically.
It is defined as the interval between two adjacent no ...
. Intervals smaller than a semitone are called
microtones. They can be formed using the notes of various kinds of non-diatonic scales. Some of the very smallest ones are called
commas, and describe small discrepancies, observed in some
tuning system
In music, there are two common meanings for tuning:
* Tuning practice, the act of tuning an instrument or voice.
* Tuning systems, the various systems of pitches used to tune an instrument, and their theoretical bases.
Tuning practice
Tun ...
s, between
enharmonically equivalent
In modern musical notation and tuning, an enharmonic equivalent is a note, interval, or key signature that is equivalent to some other note, interval, or key signature but "spelled", or named differently. The enharmonic spelling of a written no ...
notes such as C and D. Intervals can be arbitrarily small, and even imperceptible to the human ear.
In physical terms, an interval is the
ratio
In mathematics, a ratio shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
between two sonic frequencies. For example, any two notes an octave apart have a frequency ratio of 2:1. This means that successive increments of pitch by the same interval result in an exponential increase of frequency, even though the human ear perceives this as a linear increase in pitch. For this reason, intervals are often measured in
cents, a unit derived from the
logarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number to the base is the exponent to which must be raised, to produce . For example, since , the ''logarithm base'' 10 o ...
of the frequency ratio.
In Western music theory, the most common naming scheme for intervals describes two properties of the interval: the
quality
Quality may refer to:
Concepts
*Quality (business), the ''non-inferiority'' or ''superiority'' of something
*Quality (philosophy), an attribute or a property
*Quality (physics), in response theory
*Energy quality, used in various science discipli ...
(perfect, major, minor, augmented, diminished) and
number
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers c ...
(unison, second, third, etc.). Examples include the
minor third
In music theory, a minor third is a musical interval that encompasses three half steps, or semitones. Staff notation represents the minor third as encompassing three staff positions (see: interval number). The minor third is one of two com ...
or
perfect fifth
In music theory, a perfect fifth is the Interval (music), musical interval corresponding to a pair of pitch (music), pitches with a frequency ratio of 3:2, or very nearly so.
In classical music from Western culture, a fifth is the interval fro ...
. These names identify not only the difference in semitones between the upper and lower notes but also how the interval is
spelled. The importance of spelling stems from the historical practice of differentiating the frequency ratios of enharmonic intervals such as G–G and G–A.
Size
The size of an interval (also known as its width or height) can be represented using two alternative and equivalently valid methods, each appropriate to a different context: frequency ratios or cents.
Frequency ratios
The size of an interval between two notes may be measured by the
ratio
In mathematics, a ratio shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
of their
frequencies
Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from ''angular frequency''. Frequency is measured in hertz (Hz) which is eq ...
. When a
musical instrument
A musical instrument is a device created or adapted to make musical sounds. In principle, any object that produces sound can be considered a musical instrument—it is through purpose that the object becomes a musical instrument. A person who pl ...
is tuned using a
just intonation
In music, just intonation or pure intonation is the tuning of musical intervals
Interval may refer to:
Mathematics and physics
* Interval (mathematics), a range of numbers
** Partially ordered set#Intervals, its generalization from numbers to ...
tuning system, the size of the main intervals can be expressed by small-
integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language ...
ratios, such as 1:1 (
unison
In music, unison is two or more musical parts that sound either the same pitch or pitches separated by intervals of one or more octaves, usually at the same time. ''Rhythmic unison'' is another term for homorhythm.
Definition
Unison or per ...
), 2:1 (
octave
In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been refer ...
), 5:3 (
major sixth
In music from Western culture, a sixth is a musical interval encompassing six note letter names or staff positions (see Interval number for more details), and the major sixth is one of two commonly occurring sixths. It is qualified as ''major ...
), 3:2 (
perfect fifth
In music theory, a perfect fifth is the Interval (music), musical interval corresponding to a pair of pitch (music), pitches with a frequency ratio of 3:2, or very nearly so.
In classical music from Western culture, a fifth is the interval fro ...
), 4:3 (
perfect fourth
A fourth is a musical interval encompassing four staff positions in the music notation of Western culture, and a perfect fourth () is the fourth spanning five semitones (half steps, or half tones). For example, the ascending interval from C to ...
), 5:4 (
major third
In classical music, a third is a musical interval encompassing three staff positions (see Interval number for more details), and the major third () is a third spanning four semitones. Forte, Allen (1979). ''Tonal Harmony in Concept and P ...
), 6:5 (
minor third
In music theory, a minor third is a musical interval that encompasses three half steps, or semitones. Staff notation represents the minor third as encompassing three staff positions (see: interval number). The minor third is one of two com ...
). Intervals with small-integer ratios are often called ''just intervals'', or ''pure intervals''.
Most commonly, however, musical instruments are nowadays tuned using a different tuning system, called
12-tone equal temperament
Twelve-tone equal temperament (12-TET) is the musical system that divides the octave into 12 parts, all of which are equally tempered (equally spaced) on a logarithmic scale, with a ratio equal to the 12th root of 2 ( ≈ 1.05946). That resultin ...
. As a consequence, the size of most equal-tempered intervals cannot be expressed by small-integer ratios, although it is very close to the size of the corresponding just intervals. For instance, an
equal-tempered
An equal temperament is a musical temperament or tuning system, which approximates just intervals by dividing an octave (or other interval) into equal steps. This means the ratio of the frequencies of any adjacent pair of notes is the same, w ...
fifth has a frequency ratio of 2:1, approximately equal to 1.498:1, or 2.997:2 (very close to 3:2). For a comparison between the size of intervals in different tuning systems, see .
Cents
The standard system for comparing interval sizes is with
cents. The cent is a
logarithmic unit of measurement. If frequency is expressed in a
logarithmic scale
A logarithmic scale (or log scale) is a way of displaying numerical data over a very wide range of values in a compact way—typically the largest numbers in the data are hundreds or even thousands of times larger than the smallest numbers. Such a ...
, and along that scale the distance between a given frequency and its double (also called
octave
In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been refer ...
) is divided into 1200 equal parts, each of these parts is one cent. In twelve-tone
equal temperament
An equal temperament is a musical temperament or tuning system, which approximates just intervals by dividing an octave (or other interval) into equal steps. This means the ratio of the frequencies of any adjacent pair of notes is the same, wh ...
(12-TET), a tuning system in which all
semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically.
It is defined as the interval between two adjacent no ...
s have the same size, the size of one semitone is exactly 100 cents. Hence, in 12-TET the cent can be also defined as one hundredth of a
semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically.
It is defined as the interval between two adjacent no ...
.
Mathematically, the size in cents of the interval from frequency ''f''
1 to frequency ''f''
2 is
:
Main intervals
The table shows the most widely used conventional names for the intervals between the notes of a
chromatic scale
The chromatic scale (or twelve-tone scale) is a set of twelve pitches (more completely, pitch classes) used in tonal music, with notes separated by the interval of a semitone. Chromatic instruments, such as the piano, are made to produce the ...
. A
perfect unison
In music, unison is two or more musical parts that sound either the same pitch or pitches separated by intervals of one or more octaves, usually at the same time. ''Rhythmic unison'' is another term for homorhythm.
Definition
Unison or per ...
(also known as perfect prime)
["Prime (ii). See Unison"]
''Grove Music Online
''The New Grove Dictionary of Music and Musicians'' is an encyclopedic dictionary of music and musicians. Along with the German-language ''Die Musik in Geschichte und Gegenwart'', it is one of the largest reference works on the history and theo ...
''. Oxford University Press. Accessed August 2013. ) is an interval formed by two identical notes. Its size is zero
cents. A
semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically.
It is defined as the interval between two adjacent no ...
is any interval between two adjacent notes in a chromatic scale, a
whole tone
In Western music theory, a major second (sometimes also called whole tone or a whole step) is a second spanning two semitones (). A second is a musical interval encompassing two adjacent staff positions (see Interval number for more deta ...
is an interval spanning two semitones (for example, a
major second
In Western music theory, a major second (sometimes also called whole tone or a whole step) is a second spanning two semitones (). A second is a musical interval encompassing two adjacent staff positions (see Interval number for more deta ...
), and a
tritone
In music theory, the tritone is defined as a musical interval composed of three adjacent whole tones (six semitones). For instance, the interval from F up to the B above it (in short, F–B) is a tritone as it can be decomposed into the three a ...
is an interval spanning three tones, or six semitones (for example, an augmented fourth). Rarely, the term
ditone
In music, a ditone (, from , "of two tones") is the interval of a major third. The size of a ditone varies according to the sizes of the two tones of which it is compounded. The largest is the Pythagorean ditone, with a ratio of 81:64, also cal ...
is also used to indicate an interval spanning two whole tones (for example, a
major third
In classical music, a third is a musical interval encompassing three staff positions (see Interval number for more details), and the major third () is a third spanning four semitones. Forte, Allen (1979). ''Tonal Harmony in Concept and P ...
), or more strictly as a synonym of major third.
Intervals with different names may span the same number of semitones, and may even have the same width. For instance, the interval from D to F is a
major third
In classical music, a third is a musical interval encompassing three staff positions (see Interval number for more details), and the major third () is a third spanning four semitones. Forte, Allen (1979). ''Tonal Harmony in Concept and P ...
, while that from D to G is a
diminished fourth
In classical music from Western culture, a diminished fourth () is an interval produced by narrowing a perfect fourth by a chromatic semitone.Benward & Saker (2003). ''Music: In Theory and Practice, Vol. I'', p.54. . Specific example of an d4 ...
. However, they both span 4 semitones. If the
instrument is tuned so that the 12 notes of the chromatic scale are equally spaced (as in
equal temperament
An equal temperament is a musical temperament or tuning system, which approximates just intervals by dividing an octave (or other interval) into equal steps. This means the ratio of the frequencies of any adjacent pair of notes is the same, wh ...
), these intervals also have the same width. Namely, all semitones have a width of 100
cents, and all intervals spanning 4 semitones are 400 cents wide.
The names listed here cannot be determined by counting semitones alone. The rules to determine them are explained below. Other names, determined with different naming conventions, are listed in
a separate section. Intervals
smaller than one semitone (commas or microtones) and
larger than one octave (compound intervals) are introduced below.
Interval number and quality

In Western
music theory
Music theory is the study of the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory". The first is the "rudiments", that are needed to understand music notation (ke ...
, an interval is named according to its ''number'' (also called ''diatonic number'') and ''quality''. For instance, ''major third'' (or M3) is an interval name, in which the term ''major'' (M) describes the quality of the interval, and ''third'' (3) indicates its number.
Number
The number of an interval is the number of letter names or
s (lines and spaces) it encompasses, including the positions of both notes forming the interval. For instance, the interval C–G is a fifth (denoted P5) because the notes from C to the G above it encompass five letter names (C, D, E, F, G) and occupy five consecutive staff positions, including the positions of C and G. The
table
Table may refer to:
* Table (furniture), a piece of furniture with a flat surface and one or more legs
* Table (landform), a flat area of land
* Table (information), a data arrangement with rows and columns
* Table (database), how the table data ...
and the figure above show intervals with numbers ranging from 1 (e.g., P1) to 8 (e.g., P8). Intervals with larger numbers are called
compound intervals
In music theory, an interval is a difference in pitch between two sounds.
An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or h ...
.
There is a
one-to-one correspondence
In mathematics, a bijection, also known as a bijective function, one-to-one correspondence, or invertible function, is a function between the elements of two sets, where each element of one set is paired with exactly one element of the other s ...
between staff positions and diatonic-scale
degrees (the notes of
diatonic scale
In music theory, a diatonic scale is any heptatonic scale that includes five whole steps (whole tones) and two half steps (semitones) in each octave, in which the two half steps are separated from each other by either two or three whole steps, ...
).
This means that interval numbers can also be determined by counting diatonic scale degrees, rather than staff positions, provided that the two notes that form the interval are drawn from a diatonic scale. Namely, C–G is a fifth because in any diatonic scale that contains C and G, the sequence from C to G includes five notes. For instance, in the A-
major
Major (commandant in certain jurisdictions) is a military rank of commissioned officer status, with corresponding ranks existing in many military forces throughout the world. When used unhyphenated and in conjunction with no other indicators ...
diatonic scale, the five notes are C–D–E–F–G (see figure). This is not true for all kinds of scales. For instance, in a
chromatic scale
The chromatic scale (or twelve-tone scale) is a set of twelve pitches (more completely, pitch classes) used in tonal music, with notes separated by the interval of a semitone. Chromatic instruments, such as the piano, are made to produce the ...
, the notes from C to G are eight (C–C–D–D–E–F–F–G). This is the reason interval numbers are also called ''diatonic numbers'', and this convention is called ''diatonic numbering''.
If one adds any
accidentals to the notes that form an interval, by definition the notes do not change their staff positions. As a consequence, any interval has the same interval number as the corresponding
natural
Nature, in the broadest sense, is the physical world or universe. "Nature" can refer to the phenomena of the physical world, and also to life in general. The study of nature is a large, if not the only, part of science. Although humans are p ...
interval, formed by the same notes without accidentals. For instance, the intervals C–G (spanning 8 semitones) and C–G (spanning 6 semitones) are fifths, like the corresponding natural interval C–G (7 semitones).
Notice that interval numbers represent an inclusive count of encompassed staff positions or note names, not the difference between the endpoints. In other words, one starts counting the lower pitch as one, not zero. For that reason, the interval C–C, a perfect unison, is called a prime (meaning "1"), even though there is no difference between the endpoints. Continuing, the interval C–D is a second, but D is only one staff position, or diatonic-scale degree, above C. Similarly, C–E is a third, but E is only two staff positions above C, and so on. As a consequence, joining two intervals always yields an interval number one less than their sum. For instance, the intervals C–E and E–G are thirds, but joined together they form a fifth (C–G), not a sixth. Similarly, a stack of three thirds, such as C–E, E–G, and G–B, is a seventh (C–B), not a ninth.
This scheme applies to intervals up to an octave (12 semitones). For larger intervals, see below.
Quality

The name of any interval is further qualified using the terms perfect (P),
major
Major (commandant in certain jurisdictions) is a military rank of commissioned officer status, with corresponding ranks existing in many military forces throughout the world. When used unhyphenated and in conjunction with no other indicators ...
(M),
minor
Minor may refer to:
* Minor (law), a person under the age of certain legal activities.
** A person who has not reached the age of majority
* Academic minor, a secondary field of study in undergraduate education
Music theory
*Minor chord
** Barb ...
(m),
augmented (A), and
diminished (d). This is called its ''interval quality''. It is possible to have doubly diminished and doubly augmented intervals, but these are quite rare, as they occur only in
chromatic
Diatonic and chromatic are terms in music theory that are most often used to characterize scales, and are also applied to musical instruments, intervals, chords, notes, musical styles, and kinds of harmony. They are very often used as a pair, ...
contexts. The quality of a
compound interval
In music theory, an interval is a difference in pitch (music), pitch between two sounds.
An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and ...
is the quality of the simple interval on which it is based. Some other qualifiers like ''neutral'', ''subminor'', and ''supermajor'' are used for
non-diatonic intervals.
Perfect
Perfect intervals are so-called because they were traditionally considered perfectly consonant,
[ Definition of ''Perfect consonance'']
in Godfrey Weber's General music teacher, by Godfrey Weber, 1841.
although in Western classical music the perfect fourth was sometimes regarded as a less than perfect consonance, when its function was
contrapuntal
In music, counterpoint is the relationship between two or more musical lines (or voices) which are harmonically interdependent yet independent in rhythm and melodic contour. It has been most commonly identified in the European classical tradi ...
. Conversely, minor, major, augmented or diminished intervals are typically considered less consonant, and were traditionally classified as mediocre consonances, imperfect consonances, or dissonances.
Within a
diatonic scale
In music theory, a diatonic scale is any heptatonic scale that includes five whole steps (whole tones) and two half steps (semitones) in each octave, in which the two half steps are separated from each other by either two or three whole steps, ...
all unisons (P1) and octaves (P8) are perfect. Most fourths and fifths are also perfect (P4 and P5), with five and seven semitones respectively. One occurrence of a fourth is augmented (A4) and one fifth is diminished (d5), both spanning six semitones. For instance, in a C-major scale, the A4 is between F and B, and the d5 is between B and F (see table).
By definition, the
inversion
Inversion or inversions may refer to:
Arts
* , a French gay magazine (1924/1925)
* ''Inversion'' (artwork), a 2005 temporary sculpture in Houston, Texas
* Inversion (music), a term with various meanings in music theory and musical set theory
* ...
of a perfect interval is also perfect. Since the inversion does not change the
pitch class
In music, a pitch class (p.c. or pc) is a set of all pitches that are a whole number of octaves apart; for example, the pitch class C consists of the Cs in all octaves. "The pitch class C stands for all possible Cs, in whatever octave positio ...
of the two notes, it hardly affects their level of consonance (matching of their
harmonics
A harmonic is a wave with a frequency that is a positive integer multiple of the ''fundamental frequency'', the frequency of the original periodic signal, such as a sinusoidal wave. The original signal is also called the ''1st harmonic'', the ...
). Conversely, other kinds of intervals have the opposite quality with respect to their inversion. The inversion of a major interval is a minor interval, the inversion of an augmented interval is a diminished interval.
Major and minor
As shown in the table, a
diatonic scale
In music theory, a diatonic scale is any heptatonic scale that includes five whole steps (whole tones) and two half steps (semitones) in each octave, in which the two half steps are separated from each other by either two or three whole steps, ...
defines seven intervals for each interval number, each starting from a different note (seven unisons, seven seconds, etc.). The intervals formed by the notes of a diatonic scale are called diatonic. Except for unisons and octaves, the diatonic intervals with a given interval number always occur in two sizes, which differ by one semitone. For example, six of the fifths span seven semitones. The other one spans six semitones. Four of the thirds span three semitones, the others four. If one of the two versions is a perfect interval, the other is called either diminished (i.e. narrowed by one semitone) or augmented (i.e. widened by one semitone). Otherwise, the larger version is called major, the smaller one minor. For instance, since a 7-semitone fifth is a perfect interval (P5), the 6-semitone fifth is called "diminished fifth" (d5). Conversely, since neither kind of third is perfect, the larger one is called "major third" (M3), the smaller one "minor third" (m3).
Within a diatonic scale, unisons and octaves are always qualified as perfect, fourths as either perfect or augmented, fifths as perfect or diminished, and all the other intervals (seconds, thirds, sixths, sevenths) as major or minor.
Augmented and diminished
Augmented intervals are wider by one semitone than perfect or major intervals, while having the same interval number (i.e., encompassing the same number of staff positions): they are wider by a
chromatic semitone
In modern Western tonal music theory an augmented unison or augmented prime is the interval between two notes on the same staff position, or denoted by the same note letter, whose alterations cause them, in ordinary equal temperament, to be one ...
. Diminished intervals, on the other hand, are narrower by one semitone than perfect or minor intervals of the same interval number: they are narrower by a chromatic semitone. For instance, an augmented third such as C–E spans five semitones, exceeding a major third (C–E) by one semitone, while a diminished third such as C–E spans two semitones, falling short of a minor third (C–E) by one semitone.
The augmented fourth (A4) and the diminished fifth (d5) are the only augmented and diminished intervals that appear in diatonic scales (see table).
Example
Neither the number, nor the quality of an interval can be determined by counting
semitones
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically.
It is defined as the interval between two adjacent no ...
alone. As explained above, the number of staff positions must be taken into account as well.
For example, as shown in the table below, there are four semitones between A and B, between A and C, between A and D, and between A and E, but
* A–B is a second, as it encompasses two staff positions (A, B), and it is doubly augmented, as it exceeds a major second (such as A–B) by two semitones.
* A–C is a third, as it encompasses three staff positions (A, B, C), and it is major, as it spans 4 semitones.
* A–D is a fourth, as it encompasses four staff positions (A, B, C, D), and it is diminished, as it falls short of a perfect fourth (such as A–D) by one semitone.
* A-E is a fifth, as it encompasses five staff positions (A, B, C, D, E), and it is triply diminished, as it falls short of a perfect fifth (such as A–E) by three semitones.
Shorthand notation
Intervals are often abbreviated with a P for perfect, m for
minor
Minor may refer to:
* Minor (law), a person under the age of certain legal activities.
** A person who has not reached the age of majority
* Academic minor, a secondary field of study in undergraduate education
Music theory
*Minor chord
** Barb ...
, M for
major
Major (commandant in certain jurisdictions) is a military rank of commissioned officer status, with corresponding ranks existing in many military forces throughout the world. When used unhyphenated and in conjunction with no other indicators ...
, d for
diminished, A for
augmented, followed by the interval number. The indications M and P are often omitted. The
octave
In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been refer ...
is P8, and a
unison
In music, unison is two or more musical parts that sound either the same pitch or pitches separated by intervals of one or more octaves, usually at the same time. ''Rhythmic unison'' is another term for homorhythm.
Definition
Unison or per ...
is usually referred to simply as "a unison" but can be labeled P1. The
tritone
In music theory, the tritone is defined as a musical interval composed of three adjacent whole tones (six semitones). For instance, the interval from F up to the B above it (in short, F–B) is a tritone as it can be decomposed into the three a ...
, an augmented fourth or diminished fifth is often TT. The interval qualities may be also abbreviated with perf, min, maj, dim, aug. Examples:
* m2 (or min2): minor second,
* M3 (or maj3): major third,
* A4 (or aug4): augmented fourth,
* d5 (or dim5): diminished fifth,
* P5 (or perf5): perfect fifth.
Inversion
A simple interval (i.e., an interval smaller than or equal to an octave) may be
inverted by raising the lower pitch an
octave
In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been refer ...
or lowering the upper pitch an octave. For example, the fourth from a lower C to a higher F may be inverted to make a fifth, from a lower F to a higher C.
:
There are two rules to determine the number and quality of the inversion of any simple interval:
# The interval number and the number of its inversion always add up to nine (4 + 5 = 9, in the example just given).
# The inversion of a major interval is a minor interval, and vice versa; the inversion of a perfect interval is also perfect; the inversion of an augmented interval is a diminished interval, and vice versa; the inversion of a doubly augmented interval is a doubly diminished interval, and vice versa.
For example, the interval from C to the E above it is a minor third. By the two rules just given, the interval from E to the C above it must be a major sixth.
Since compound intervals are larger than an octave, "the inversion of any compound interval is always the same as the inversion of the simple interval from which it is compounded."
For intervals identified by their ratio, the inversion is determined by reversing the ratio and multiplying the ratio by 2 until it is greater than 1. For example, the inversion of a 5:4 ratio is an 8:5 ratio.
For intervals identified by an integer number of semitones, the inversion is obtained by subtracting that number from 12.
Since an
interval class
In musical set theory, an interval class (often abbreviated: ic), also known as unordered pitch-class interval, interval distance, undirected interval, or "(even completely incorrectly) as 'interval mod 6'" (; ), is the shortest distance in pitch ...
is the lower number selected among the interval integer and its inversion, interval classes cannot be inverted.
Classification
Intervals can be described, classified, or compared with each other according to various criteria.
Melodic and harmonic
An interval can be described as
* Vertical or
harmonic
A harmonic is a wave with a frequency that is a positive integer multiple of the ''fundamental frequency'', the frequency of the original periodic signal, such as a sinusoidal wave. The original signal is also called the ''1st harmonic'', the ...
if the two notes sound simultaneously
* Horizontal, linear, or
melodic
A melody (from Greek μελῳδία, ''melōidía'', "singing, chanting"), also tune, voice or line, is a linear succession of musical tones that the listener perceives as a single entity. In its most literal sense, a melody is a combinat ...
if they sound successively.
Melodic intervals can be ''ascending'' (lower pitch precedes higher pitch) or ''descending''.
Diatonic and chromatic
In general,
* A ''
diatonic
Diatonic and chromatic are terms in music theory that are most often used to characterize Scale (music), scales, and are also applied to musical instruments, Interval (music), intervals, Chord (music), chords, Musical note, notes, musical sty ...
interval'' is an interval formed by two notes of a
diatonic scale
In music theory, a diatonic scale is any heptatonic scale that includes five whole steps (whole tones) and two half steps (semitones) in each octave, in which the two half steps are separated from each other by either two or three whole steps, ...
.
* A ''chromatic interval'' is a non-diatonic interval formed by two notes of a
chromatic scale
The chromatic scale (or twelve-tone scale) is a set of twelve pitches (more completely, pitch classes) used in tonal music, with notes separated by the interval of a semitone. Chromatic instruments, such as the piano, are made to produce the ...
.

The table
above depicts the 56 diatonic intervals formed by the notes of the C major scale (a diatonic scale). Notice that these intervals, as well as any other diatonic interval, can be also formed by the notes of a chromatic scale.
The distinction between diatonic and chromatic intervals is controversial, as it is based on the definition of diatonic scale, which is variable in the literature. For example, the interval B–E (a
diminished fourth
In classical music from Western culture, a diminished fourth () is an interval produced by narrowing a perfect fourth by a chromatic semitone.Benward & Saker (2003). ''Music: In Theory and Practice, Vol. I'', p.54. . Specific example of an d4 ...
, occurring in the
harmonic C-minor scale) is considered diatonic if the harmonic minor scales are considered diatonic as well. Otherwise, it is considered chromatic. For further details, see the
main article.
By a commonly used definition of diatonic scale (which excludes the
harmonic minor
In music theory, the minor scale is three scale patterns – the natural minor scale (or Aeolian mode), the harmonic minor scale, and the melodic minor scale (ascending or descending) – rather than just two as with the major scale, which also ...
and
melodic minor
In music theory, the minor scale is three scale patterns – the natural minor scale (or Aeolian mode), the harmonic minor scale, and the melodic minor scale (ascending or descending) – rather than just two as with the major scale, which also ...
scales), all perfect, major and minor intervals are diatonic. Conversely, no augmented or diminished interval is diatonic, except for the augmented fourth and diminished fifth.

The distinction between diatonic and chromatic intervals may be also sensitive to context. The above-mentioned 56 intervals formed by the C-major scale are sometimes called ''diatonic to C major''. All other intervals are called ''chromatic to C major''. For instance, the perfect fifth A–E is chromatic to C major, because A and E are not contained in the C major scale. However, it is diatonic to others, such as the A major scale.
Consonant and dissonant
Consonance and dissonance
In music, consonance and dissonance are categorizations of simultaneous or successive Sound, sounds. Within the Western tradition, some listeners associate consonance with sweetness, pleasantness, and acceptability, and dissonance with harshness ...
are relative terms that refer to the stability, or state of repose, of particular musical effects. Dissonant intervals are those that cause tension and desire to be ''resolved'' to consonant intervals.
These terms are relative to the usage of different compositional styles.
* In
15th- and 16th-century usage, perfect fifths and octaves, and major and minor thirds and sixths were considered harmonically consonant, and all other intervals dissonant, including the perfect fourth, which by 1473 was described (by
Johannes Tinctoris
Jehan le Taintenier or Jean Teinturier (Latinised as Johannes Tinctoris; also Jean de Vaerwere; – 1511) was a Renaissance music theorist and composer from the Low Countries. Up to his time, he is perhaps the most significant European writer ...
) as dissonant, except between the upper parts of a vertical sonority—for example, with a supporting third below ("6-3 chords"). In the
common practice period
In European art music, the common-practice period is the era of the tonal system. Most of its features persisted from the mid- Baroque period through the Classical and Romantic periods, roughly from 1650 to 1900. There was much stylistic evoluti ...
, it makes more sense to speak of consonant and dissonant chords, and certain intervals previously considered dissonant (such as minor sevenths) became acceptable in certain contexts. However, 16th-century practice was still taught to beginning musicians throughout this period.
*
Hermann von Helmholtz
Hermann Ludwig Ferdinand von Helmholtz (31 August 1821 – 8 September 1894) was a German physicist and physician who made significant contributions in several scientific fields, particularly hydrodynamic stability. The Helmholtz Association, ...
(1821–1894) theorised that dissonance was caused by the presence of
beats. von Helmholtz further believed that the beating produced by the upper partials of harmonic sounds was the cause of dissonance for intervals too far apart to produce beating between the
fundamentals. von Helmholtz then designated that two harmonic tones that shared common low partials would be more consonant, as they produced less beats. von Helmholtz disregarded partials above the seventh, as he believed that they were not audible enough to have significant effect. From this von Helmholtz categorises the octave, perfect fifth, perfect fourth, major sixth, major third, and minor third as consonant, in decreasing value, and other intervals as dissonant.
*
David Cope
David Cope (born May 17, 1941 in San Francisco, California) is an American author, composer, scientist, and former professor of music at the University of California, Santa Cruz (UCSC). His primary area of research involves artificial intellige ...
(1997) suggests the concept of interval strength,
[ Cope, David (1997). ''Techniques of the Contemporary Composer'', pp. 40–41. New York, New York: Schirmer Books. .] in which an interval's strength, consonance, or stability is determined by its approximation to a lower and stronger, or higher and weaker, position in the
harmonic series. See also:
Lipps–Meyer law and
#Interval root
All of the above analyses refer to vertical (simultaneous) intervals.
Simple and compound

A simple interval is an interval spanning at most one octave (see
Main intervals above). Intervals spanning more than one octave are called compound intervals, as they can be obtained by adding one or more octaves to a simple interval (see
below
Below may refer to:
*Earth
*Ground (disambiguation)
*Soil
*Floor
*Bottom (disambiguation)
Bottom may refer to:
Anatomy and sex
* Bottom (BDSM), the partner in a BDSM who takes the passive, receiving, or obedient role, to that of the top or ...
for details).
Steps and skips
Linear (melodic) intervals may be described as ''steps'' or ''skips''. A ''step'', or ''conjunct motion'',
[
Bonds, Mark Evan (2006).
''A History of Music in Western Culture'', p.123. 2nd ed. .]
is a linear interval between two consecutive notes of a scale. Any larger interval is called a ''skip'' (also called a ''leap''), or ''disjunct motion''.
In the
diatonic scale
In music theory, a diatonic scale is any heptatonic scale that includes five whole steps (whole tones) and two half steps (semitones) in each octave, in which the two half steps are separated from each other by either two or three whole steps, ...
, a step is either a
minor second
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically.
It is defined as the interval between two adjacent no ...
(sometimes also called ''half step'') or
major second
In Western music theory, a major second (sometimes also called whole tone or a whole step) is a second spanning two semitones (). A second is a musical interval encompassing two adjacent staff positions (see Interval number for more deta ...
(sometimes also called ''whole step''), with all intervals of a
minor third
In music theory, a minor third is a musical interval that encompasses three half steps, or semitones. Staff notation represents the minor third as encompassing three staff positions (see: interval number). The minor third is one of two com ...
or larger being skips.
For example, C to D (major second) is a step, whereas C to E (
major third
In classical music, a third is a musical interval encompassing three staff positions (see Interval number for more details), and the major third () is a third spanning four semitones. Forte, Allen (1979). ''Tonal Harmony in Concept and P ...
) is a skip.
More generally, a step is a smaller or narrower interval in a musical line, and a skip is a wider or larger interval, where the categorization of intervals into steps and skips is determined by the
tuning system
In music, there are two common meanings for tuning:
* Tuning practice, the act of tuning an instrument or voice.
* Tuning systems, the various systems of pitches used to tune an instrument, and their theoretical bases.
Tuning practice
Tun ...
and the
pitch space
In music theory, pitch spaces model relationships between pitches. These models typically use distance to model the degree of relatedness, with closely related pitches placed near one another, and less closely related pitches placed farther apa ...
used.
Melodic motion
Melodic motion is the quality of movement of a melody, including nearness or farness of successive pitches or notes in a melody. This may be described as conjunct or disjunct, stepwise, skipwise or no movement, respectively. See also contrapunta ...
in which the interval between any two consecutive pitches is no more than a step, or, less strictly, where skips are rare, is called ''stepwise'' or ''conjunct'' melodic motion, as opposed to ''skipwise'' or ''disjunct'' melodic motions, characterized by frequent skips.
Enharmonic intervals
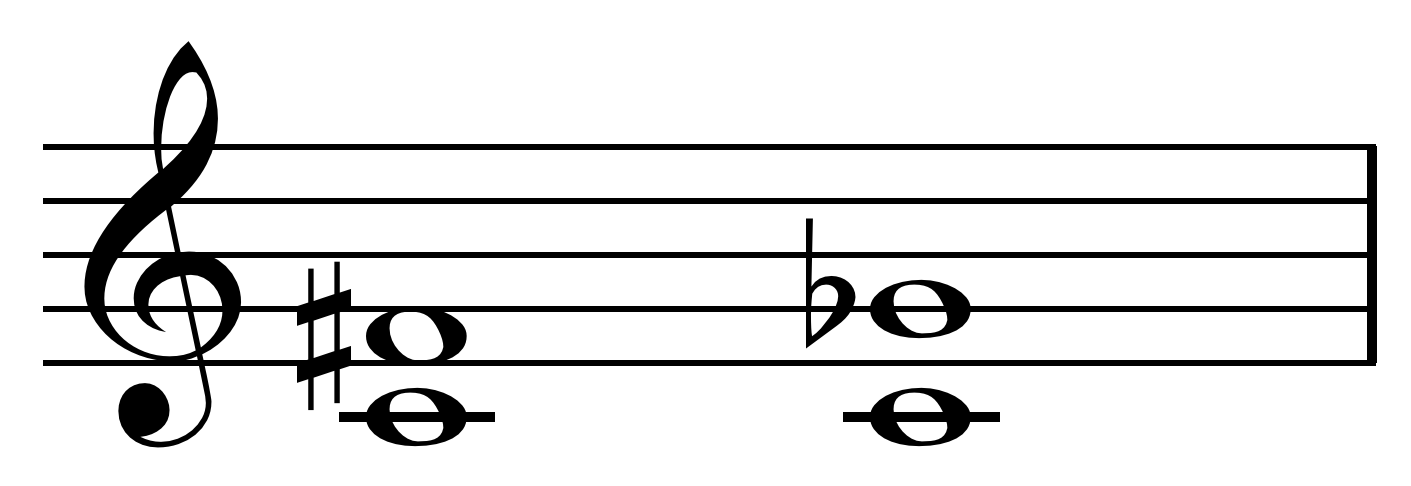
Two intervals are considered ''
enharmonic
In modern musical notation and tuning, an enharmonic equivalent is a note, interval, or key signature that is equivalent to some other note, interval, or key signature but "spelled", or named differently. The enharmonic spelling of a written n ...
'', or ''enharmonically equivalent'', if they both contain the same
pitches spelled in different ways; that is, if the notes in the two intervals are themselves enharmonically equivalent. Enharmonic intervals span the same number of
semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically.
It is defined as the interval between two adjacent no ...
s.
For example, the four intervals listed in the table below are all enharmonically equivalent, because the notes F and G indicate the same pitch, and the same is true for A and B. All these intervals span four semitones.
When played as isolated chords on a
piano keyboard
A musical keyboard is the set of adjacent depressible levers or keys on a musical instrument. Keyboards typically contain keys for playing the twelve notes of the Western musical scale, with a combination of larger, longer keys and smaller, sho ...
, these intervals are indistinguishable to the ear, because they are all played with the same two keys. However, in a musical context, the
diatonic function
In music, function (also referred to as harmonic function) is a term used to denote the relationship of a chord"Function", unsigned article, ''Grove Music Online'', . or a scale degree to a tonal centre. Two main theories of tonal functions ex ...
of the notes these intervals incorporate is very different.
The discussion above assumes the use of the prevalent tuning system,
12-tone equal temperament
Twelve-tone equal temperament (12-TET) is the musical system that divides the octave into 12 parts, all of which are equally tempered (equally spaced) on a logarithmic scale, with a ratio equal to the 12th root of 2 ( ≈ 1.05946). That resultin ...
("12-TET"). But in other historic
meantone temperament
Meantone temperament is a musical temperament, that is a tuning system, obtained by narrowing the fifths so that their ratio is slightly less than 3:2 (making them ''narrower'' than a perfect fifth), in order to push the thirds closer to pure. Me ...
s, the pitches of pairs of notes such as F and G may not necessarily coincide. These two notes are enharmonic in 12-TET, but may not be so in another tuning system. In such cases, the intervals they form would also not be enharmonic. For example, in
quarter-comma meantone
Quarter-comma meantone, or -comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. In this system the perfect fifth is flattened by one quarter of a syntonic comma (81:80 ...
, all four intervals shown in the example above would be different.
Minute intervals

There are also a number of minute intervals not found in the chromatic scale or labeled with a diatonic function, which have names of their own. They may be described as
microtones, and some of them can be also classified as
comma
The comma is a punctuation mark that appears in several variants in different languages. It has the same shape as an apostrophe or single closing quotation mark () in many typefaces, but it differs from them in being placed on the baseline ...
s, as they describe small discrepancies, observed in some tuning systems, between
enharmonically equivalent
In modern musical notation and tuning, an enharmonic equivalent is a note, interval, or key signature that is equivalent to some other note, interval, or key signature but "spelled", or named differently. The enharmonic spelling of a written no ...
notes. In the following list, the interval sizes in
cents are approximate.
* A ''
Pythagorean comma
In musical tuning, the Pythagorean comma (or ditonic comma), named after the ancient mathematician and philosopher Pythagoras, is the small interval (or comma) existing in Pythagorean tuning between two enharmonically equivalent notes such as C ...
'' is the difference between twelve justly tuned perfect fifths and seven octaves. It is expressed by the
frequency
Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from ''angular frequency''. Frequency is measured in hertz (Hz) which is eq ...
ratio 531441:524288 (23.5 cents).
* A ''
syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the Didymean comma, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80 (= 1.0125) ( ...
'' is the difference between four justly tuned perfect fifths and two octaves plus a major third. It is expressed by the ratio 81:80 (21.5 cents).
* A ''
septimal comma
A septimal comma is a small musical interval in just intonation that contains the number seven in its prime factorization. There is more than one such interval, so the term ''septimal comma'' is ambiguous, but it most commonly refers to the in ...
'' is 64:63 (27.3 cents), and is the difference between the Pythagorean or 3-limit "7th" and the "harmonic 7th".
* A ''
diesis
In classical music from Western culture, a diesis ( , plural dieses ( , "difference"; Greek: δίεσις "leak" or "escape"Benson, Dave (2006). ''Music: A Mathematical Offering'', p.171. . Based on the technique of playing the aulos, where p ...
'' is generally used to mean the difference between three justly tuned major thirds and one octave. It is expressed by the ratio 128:125 (41.1 cents). However, it has been used to mean other small intervals: see
diesis
In classical music from Western culture, a diesis ( , plural dieses ( , "difference"; Greek: δίεσις "leak" or "escape"Benson, Dave (2006). ''Music: A Mathematical Offering'', p.171. . Based on the technique of playing the aulos, where p ...
for details.
* A ''
diaschisma
The diaschisma (or diacisma) is a small musical interval defined as the difference between three octaves and four perfect fifths plus two major thirds (in just intonation). It can be represented by the ratio 2048:2025 and is about 19.5 cents. ...
'' is the difference between three octaves and four justly tuned perfect fifths plus two justly tuned major thirds. It is expressed by the ratio 2048:2025 (19.6 cents).
* A ''
schisma
In music, the schisma (also spelled ''skhisma'') is the interval between a Pythagorean comma (531441:524288) and a syntonic comma (81:80) and equals or 32805:32768 = 1.00113, which is 1.9537 cents (). It may also be defined as:
* the differe ...
'' (also skhisma) is the difference between five octaves and eight justly tuned fifths plus one justly tuned major third. It is expressed by the ratio 32805:32768 (2.0 cents). It is also the difference between the Pythagorean and syntonic commas. (A schismic major third is a schisma different from a just major third, eight fifths down and five octaves up, F in C.)
* A ''
kleisma
In music theory and tuning, the kleisma (κλείσμα), or semicomma majeur, is a minute and barely perceptible comma type interval important to musical temperaments. It is the difference between six justly tuned minor thirds (each with a freq ...
'' is the difference between six
minor third
In music theory, a minor third is a musical interval that encompasses three half steps, or semitones. Staff notation represents the minor third as encompassing three staff positions (see: interval number). The minor third is one of two com ...
s and one ''tritave'' or ''perfect twelfth'' (an
octave
In music, an octave ( la, octavus: eighth) or perfect octave (sometimes called the diapason) is the interval between one musical pitch and another with double its frequency. The octave relationship is a natural phenomenon that has been refer ...
plus a
perfect fifth
In music theory, a perfect fifth is the Interval (music), musical interval corresponding to a pair of pitch (music), pitches with a frequency ratio of 3:2, or very nearly so.
In classical music from Western culture, a fifth is the interval fro ...
), with a frequency ratio of 15625:15552 (8.1 cents) ().
* A ''
septimal kleisma
In music, the ratio 225/224 is called the septimal kleisma ().
It is a minute comma type interval of approximately 7.7 cents. Factoring it into primes gives 2−5 32 52 7−1, which can be rewritten 2−1 (5/4)2 (9/7). That says t ...
'' is the amount that two major thirds of 5:4 and a septimal major third, or supermajor third, of 9:7 exceeds the octave. Ratio 225:224 (7.7 cents).
* A ''
quarter tone
A quarter tone is a pitch halfway between the usual notes of a chromatic scale or an interval about half as wide (aurally, or logarithmically) as a semitone, which itself is half a whole tone. Quarter tones divide the octave by 50 cents each, a ...
'' is half the width of a
semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically.
It is defined as the interval between two adjacent no ...
, which is half the width of a
whole tone
In Western music theory, a major second (sometimes also called whole tone or a whole step) is a second spanning two semitones (). A second is a musical interval encompassing two adjacent staff positions (see Interval number for more deta ...
. It is equal to exactly 50 cents.
Compound intervals

A compound interval is an interval spanning more than one octave.
Conversely, intervals spanning at most one octave are called simple intervals (see
Main intervals below).
In general, a compound interval may be defined by a sequence or "stack" of two or more simple intervals of any kind. For instance, a major tenth (two staff positions above one octave), also called ''compound major third'', spans one octave plus one major third.
Any compound interval can be always decomposed into one or more octaves plus one simple interval. For instance, a major seventeenth can be decomposed into two octaves and one major third, and this is the reason why it is called a compound major third, even when it is built by adding up four fifths.
The diatonic number ''DN''
c of a compound interval formed from ''n'' simple intervals with diatonic numbers ''DN''
1, ''DN''
2, ..., ''DN''
n, is determined by:
:
which can also be written as:
:
The quality of a compound interval is determined by the quality of the simple interval on which it is based. For instance, a compound major third is a major tenth (1+(8−1)+(3−1) = 10), or a major seventeenth (1+(8−1)+(8−1)+(3−1) = 17), and a compound perfect fifth is a perfect twelfth (1+(8−1)+(5−1) = 12) or a perfect nineteenth (1+(8−1)+(8−1)+(5−1) = 19). Notice that two octaves are a fifteenth, not a sixteenth (1+(8−1)+(8−1) = 15). Similarly, three octaves are a twenty-second (1+3×(8−1) = 22), and so on.
Main compound intervals
It is also worth mentioning here the major seventeenth (28 semitones)—an interval larger than two octaves that can be considered a multiple of a perfect fifth (7 semitones) as it can be decomposed into four perfect fifths (7 × 4 = 28 semitones), or two octaves plus a major third (12 + 12 + 4 = 28 semitones). Intervals larger than a major seventeenth seldom come up, most often being referred to by their compound names, for example "two octaves plus a fifth" rather than "a 19th".
Intervals in chords
Chords are sets of three or more notes. They are typically defined as the combination of intervals starting from a common note called the
root
In vascular plants, the roots are the organs of a plant that are modified to provide anchorage for the plant and take in water and nutrients into the plant body, which allows plants to grow taller and faster. They are most often below the sur ...
of the chord. For instance a
major triad
In music theory, a major chord is a chord that has a root, a major third, and a perfect fifth. When a chord comprises only these three notes, it is called a major triad. For example, the major triad built on C, called a C major triad, has pitch ...
is a chord containing three notes defined by the root and two intervals (major third and perfect fifth). Sometimes even a single interval (
dyad
Dyad or dyade may refer to:
Arts and entertainment
* Dyad (music), a set of two notes or pitches
* ''Dyad'' (novel), by Michael Brodsky, 1989
* ''Dyad'' (video game), 2012
* ''Dyad 1909'' and ''Dyad 1929'', ballets by Wayne McGregor
Other uses ...
) is considered a chord.
[ Károlyi, Ottó (1965), ''Introducing Music'', p. 63. Hammondsworth (England), and New York: Penguin Books. .] Chords are classified based on the quality and number of the intervals that define them.
Chord qualities and interval qualities
The main chord qualities are
major
Major (commandant in certain jurisdictions) is a military rank of commissioned officer status, with corresponding ranks existing in many military forces throughout the world. When used unhyphenated and in conjunction with no other indicators ...
,
minor
Minor may refer to:
* Minor (law), a person under the age of certain legal activities.
** A person who has not reached the age of majority
* Academic minor, a secondary field of study in undergraduate education
Music theory
*Minor chord
** Barb ...
,
augmented,
diminished,
half-diminished, and
dominant.
The
symbols
A symbol is a mark, sign, or word that indicates, signifies, or is understood as representing an idea, object, or relationship. Symbols allow people to go beyond what is known or seen by creating linkages between otherwise very different conc ...
used for chord quality are similar to those used for interval quality (see above). In addition, + or aug is used for augmented, ° or dim for diminished, for half diminished, and dom for dominant (the symbol − alone is not used for diminished).
Deducing component intervals from chord names and symbols
The main rules to decode chord ''names or symbols'' are summarized below. Further details are given at
Rules to decode chord names and symbols.
# For 3-note chords (
triads),
major
Major (commandant in certain jurisdictions) is a military rank of commissioned officer status, with corresponding ranks existing in many military forces throughout the world. When used unhyphenated and in conjunction with no other indicators ...
or
minor
Minor may refer to:
* Minor (law), a person under the age of certain legal activities.
** A person who has not reached the age of majority
* Academic minor, a secondary field of study in undergraduate education
Music theory
*Minor chord
** Barb ...
always refer to the interval of the third above the
root note
In music theory, the concept of root is the idea that a chord can be represented and named by one of its notes. It is linked to harmonic thinking—the idea that vertical aggregates of notes can form a single unit, a chord. It is in this sense ...
, while
augmented and
diminished always refer to the interval of the fifth above root. The same is true for the corresponding symbols (e.g., Cm means C
m3, and C+ means C
+5). Thus, the terms third and
fifth and the corresponding symbols 3 and 5 are typically omitted. This rule can be generalized to all kinds of chords, provided the above-mentioned qualities appear immediately after the root note, or at the beginning of the chord name or symbol. For instance, in the chord symbols Cm and Cm
7, m refers to the interval m3, and 3 is omitted. When these qualities do not appear immediately after the root note, or at the beginning of the name or symbol, they should be considered
interval qualities, rather than chord qualities. For instance, in Cm
M7 (
minor major seventh chord
A minor major seventh chord, or minor/major seventh chord (also known as the Hitchcock Chord) is a seventh chord composed of a Root (chord), root, minor third, perfect fifth, and major seventh (1, 3, 5, and 7). It can be viewed as a minor triad w ...
), m is the chord quality and refers to the m3 interval, while M refers to the M7 interval. When the
number
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers c ...
of an extra interval is specified immediately after chord quality, the quality of that interval may coincide with chord quality (e.g., CM
7 = CM
M7). However, this is not always true (e.g., Cm
6 = Cm
M6, C+
7 = C+
m7, CM
11 = CM
P11). See
main article for further details.
# Without contrary information, a
major third
In classical music, a third is a musical interval encompassing three staff positions (see Interval number for more details), and the major third () is a third spanning four semitones. Forte, Allen (1979). ''Tonal Harmony in Concept and P ...
interval and a
perfect fifth
In music theory, a perfect fifth is the Interval (music), musical interval corresponding to a pair of pitch (music), pitches with a frequency ratio of 3:2, or very nearly so.
In classical music from Western culture, a fifth is the interval fro ...
interval (
major triad
In music theory, a major chord is a chord that has a root, a major third, and a perfect fifth. When a chord comprises only these three notes, it is called a major triad. For example, the major triad built on C, called a C major triad, has pitch ...
) are implied. For instance, a C chord is a C major triad, and the name C minor seventh (Cm
7) implies a minor 3rd by rule 1, a perfect 5th by this rule, and a
minor 7th
In music theory, a minor seventh is one of two musical intervals that span seven staff positions. It is ''minor'' because it is the smaller of the two sevenths, spanning ten semitones. The major seventh spans eleven. For example, the interval ...
by definition (see below). This rule has one exception (see next rule).
# When the fifth interval is
diminished, the third must be minor. This rule overrides rule 2. For instance, Cdim
7 implies a diminished 5th by rule 1, a minor 3rd by this rule, and a diminished 7th by definition (see below).
#Names and symbols that contain only a plain
interval number
In music theory, an interval is a difference in pitch between two sounds.
An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or ha ...
(e.g., “seventh chord”) or the
chord root and a number (e.g., “C seventh”, or C
7) are interpreted as follows:
#*If the number is 2, 4, 6, etc., the chord is a major
added tone chord
An added tone chord, or added note chord, is a non- tertian chord composed of a triad and an extra "added" note. Any tone that is not a seventh factor is commonly categorized as an added tone. It can be outside the tertian sequence of ascendin ...
(e.g., C
6 = C
M6 = C
add6) and contains, together with the implied major triad, an extra
major 2nd
''Major 2nd'' (stylized as ''MAJOR 2nd'') is a Japanese sports manga series written and illustrated by Takuya Mitsuda. It is a sequel to the original manga series '' Major''. It has been serialized in Shogakukan's ''Weekly Shōnen Sunday'' s ...
,
perfect 4th
A fourth is a musical interval encompassing four staff positions in the music notation of Western culture, and a perfect fourth () is the fourth spanning five semitones (half steps, or half tones). For example, the ascending interval from C to ...
, or
major 6th
In music from Western culture, a sixth is a interval (music), musical interval encompassing six note letter names or staff positions (see Interval (music)#Number, Interval number for more details), and the major sixth is one of two commonly occ ...
(see
names and symbols for added tone chords).
#*If the number is 7, 9, 11, 13, etc., the chord is
dominant (e.g., C
7 = C
dom7) and contains, together with the implied major triad, one or more of the following extra intervals: minor 7th, major 9th, perfect 11th, and major 13th (see names and symbols for
seventh
Seventh is the ordinal form of the number seven.
Seventh may refer to:
* Seventh Amendment to the United States Constitution
* A fraction (mathematics), , equal to one of seven equal parts
Film and television
*"The Seventh", a second-season e ...
and
extended chords
In music, extended chords are certain chords (built from thirds) or triads with notes ''extended'', or added, beyond the seventh. Ninth, eleventh, and thirteenth chords are extended chords. The thirteenth is the farthest extension diatonical ...
).
#*If the number is 5, the chord (technically not a chord in the traditional sense, but a
dyad
Dyad or dyade may refer to:
Arts and entertainment
* Dyad (music), a set of two notes or pitches
* ''Dyad'' (novel), by Michael Brodsky, 1989
* ''Dyad'' (video game), 2012
* ''Dyad 1909'' and ''Dyad 1929'', ballets by Wayne McGregor
Other uses ...
) is a
power chord
A power chord (also fifth chord) is a colloquial name for a chord in guitar music, especially electric guitar, that consists of the root note and the fifth, as well as possibly octaves of those notes. Power chords are commonly played on am ...
. Only the root, a perfect fifth and usually an octave are played.
The table shows the intervals contained in some of the main chords (component intervals), and some of the symbols used to denote them. The interval qualities or numbers in
boldface
In typography, emphasis is the strengthening of words in a text with a font in a different style from the rest of the text, to highlight them. It is the equivalent of prosody stress in speech.
Methods and use
The most common methods in W ...
font can be deduced from chord name or symbol by applying rule 1. In symbol examples, C is used as chord root.
Size of intervals used in different tuning systems
In this table, the interval widths used in four different tuning systems are compared. To facilitate comparison,
just interval
In music, just intonation or pure intonation is the tuning of musical intervals as whole number ratios (such as 3:2 or 4:3) of frequencies. An interval tuned in this way is said to be pure, and is called a just interval. Just intervals (and c ...
s as provided by 5-limit tuning (see
symmetric scale n.1) are shown in
bold
In typography, emphasis is the strengthening of words in a text with a font in a different style from the rest of the text, to highlight them. It is the equivalent of prosody stress in speech.
Methods and use
The most common methods in W ...
font, and the values in cents are
rounded to integers. Notice that in each of the
non-equal tuning systems, by definition the width of ''each'' type of interval (including the semitone) changes depending on the note that starts the interval. This is the art of
just intonation
In music, just intonation or pure intonation is the tuning of musical intervals
Interval may refer to:
Mathematics and physics
* Interval (mathematics), a range of numbers
** Partially ordered set#Intervals, its generalization from numbers to ...
. In
equal temperament
An equal temperament is a musical temperament or tuning system, which approximates just intervals by dividing an octave (or other interval) into equal steps. This means the ratio of the frequencies of any adjacent pair of notes is the same, wh ...
, the intervals are never precisely in tune with each other. This is the price of using equidistant intervals in a 12-tone scale. For simplicity, for some types of interval the table shows only one value (the
most often observed one).
In
-comma meantone, by definition 11 perfect fifths have a size of approximately 697 cents (700 − ''ε'' cents, where ''ε'' ≈ 3.42 cents); since the average size of the 12 fifths must equal exactly 700 cents (as in equal temperament), the other one must have a size of about 738 cents (700 + 11''ε'', the
wolf fifth
In music theory, the wolf fifth (sometimes also called Procrustean fifth,
or imperfect fifth)
Paul, Oscar (1885). A manual of harmony for use in music-schools and seminaries and for self-instruction', p.165. Theodore Baker, trans. G. Schirmer. ...
or
diminished sixth
In classical music from Western culture, a diminished sixth () is an interval produced by narrowing a minor sixth by a chromatic semitone.Benward & Saker (2003). ''Music: In Theory and Practice, Vol. I'', p.54. . Specific example of an d6 not ...
); 8 major thirds have size about 386 cents (400 − 4''ε''), 4 have size about 427 cents (400 + 8''ε'', actually
diminished fourth
In classical music from Western culture, a diminished fourth () is an interval produced by narrowing a perfect fourth by a chromatic semitone.Benward & Saker (2003). ''Music: In Theory and Practice, Vol. I'', p.54. . Specific example of an d4 ...
s), and their average size is 400 cents. In short, similar differences in width are observed for all interval types, except for unisons and octaves, and they are all multiples of ε (the difference between the -comma meantone fifth and the average fifth). A more detailed analysis is provided at
-comma meantone Size of intervals. Note that -comma meantone was designed to produce just major thirds, but only 8 of them are just (5:4, about 386 cents).
The
Pythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2.Bruce Benward and Marilyn Nadine Saker (2003). ''Music: In Theory and Practice'', seventh edition, 2 vols. (Boston: Mc ...
is characterized by smaller differences because they are multiples of a smaller ''ε'' (''ε'' ≈ 1.96 cents, the difference between the Pythagorean fifth and the average fifth). Notice that here the fifth is wider than 700 cents, while in most
meantone temperament
Meantone temperament is a musical temperament, that is a tuning system, obtained by narrowing the fifths so that their ratio is slightly less than 3:2 (making them ''narrower'' than a perfect fifth), in order to push the thirds closer to pure. Me ...
s, including -comma meantone, it is tempered to a size smaller than 700. A more detailed analysis is provided at .
The
5-limit tuning
Five-limit tuning, 5-limit tuning, or 5-prime-limit tuning (not to be confused with 5-odd-limit tuning), is any system for tuning a musical instrument that obtains the frequency of each note by multiplying the frequency of a given reference note ...
system uses just tones and semitones as building blocks, rather than a stack of perfect fifths, and this leads to even more varied intervals throughout the scale (each kind of interval has three or four different sizes). A more detailed analysis is provided at . Note that 5-limit tuning was designed to maximize the number of just intervals, but even in this system some intervals are not just (e.g., 3 fifths, 5 major thirds and 6 minor thirds are not just; also, 3 major and 3 minor thirds are
wolf interval
In music theory, the wolf fifth (sometimes also called Procrustean fifth,
or imperfect fifth)
Paul, Oscar (1885). A manual of harmony for use in music-schools and seminaries and for self-instruction', p.165. Theodore Baker, trans. G. Schirmer. ...
s).
The above-mentioned symmetric scale 1, defined in the 5-limit tuning system, is not the only method to obtain
just intonation
In music, just intonation or pure intonation is the tuning of musical intervals
Interval may refer to:
Mathematics and physics
* Interval (mathematics), a range of numbers
** Partially ordered set#Intervals, its generalization from numbers to ...
. It is possible to construct juster intervals or just intervals closer to the equal-tempered equivalents, but most of the ones listed above have been used historically in equivalent contexts. In particular, the
asymmetric version of the 5-limit tuning scale provides a juster value for the minor seventh (9:5, rather than 16:9). Moreover, the
tritone
In music theory, the tritone is defined as a musical interval composed of three adjacent whole tones (six semitones). For instance, the interval from F up to the B above it (in short, F–B) is a tritone as it can be decomposed into the three a ...
(augmented fourth or diminished fifth), could have other just ratios; for instance, 7:5 (about 583 cents) or 17:12 (about 603 cents) are possible alternatives for the augmented fourth (the latter is fairly common, as it is closer to the equal-tempered value of 600 cents). The 7:4 interval (about 969 cents), also known as the
harmonic seventh
The harmonic seventh interval, also known as the septimal minor seventh, or subminor seventh, is one with an exact 7:4 ratio (about 969 cents). This is somewhat narrower than and is, "particularly sweet", "sweeter in quality" than an "ordinar ...
, has been a contentious issue throughout the history of music theory; it is 31 cents flatter than an equal-tempered minor seventh. For further details about reference ratios, see .
In the diatonic system, every interval has one or more ''
enharmonic
In modern musical notation and tuning, an enharmonic equivalent is a note, interval, or key signature that is equivalent to some other note, interval, or key signature but "spelled", or named differently. The enharmonic spelling of a written n ...
equivalents'', such as
augmented second
In classical music from Western culture, an augmented second is an interval that, in equal temperament, is sonically equivalent to a minor third, spanning three semitones, and is created by widening a major second by a chromatic semitone.Benwar ...
for
minor third
In music theory, a minor third is a musical interval that encompasses three half steps, or semitones. Staff notation represents the minor third as encompassing three staff positions (see: interval number). The minor third is one of two com ...
.
Interval root
Although intervals are usually designated in relation to their lower note,
David Cope
David Cope (born May 17, 1941 in San Francisco, California) is an American author, composer, scientist, and former professor of music at the University of California, Santa Cruz (UCSC). His primary area of research involves artificial intellige ...
and
Hindemith
Paul Hindemith (; 16 November 189528 December 1963) was a German composer, music theorist, teacher, violist and conductor. He founded the Amar Quartet in 1921, touring extensively in Europe. As a composer, he became a major advocate of the ' ...
both suggest the concept of interval root. To determine an interval's root, one locates its nearest approximation in the harmonic series. The root of a perfect fourth, then, is its ''top'' note because it is an octave of the fundamental in the hypothetical harmonic series. The bottom note of every odd diatonically numbered intervals are the roots, as are the tops of all even numbered intervals. The root of a collection of intervals or a chord is thus determined by the interval root of its strongest interval.
As to its usefulness, Cope
provides the example of the final tonic chord of some popular music being traditionally analyzable as a "submediant six-five chord" (
added sixth chord
The term ''sixth chord'' refers to two different kinds of chord, the first in classical music and the second in modern popular music.
The original meaning of the term is a ''chord in first inversion'', in other words with its third in the bass a ...
s by popular terminology), or a
first inversion
The first inversion of a chord is the voicing of a triad, seventh chord, or ninth chord in which the third of the chord is the bass note and the root a sixth above it.Walter Piston, ''Harmony'', fifth edition, revised and expanded by Mark DeVo ...
seventh chord (possibly the dominant of the mediant V/iii). According to the interval root of the strongest interval of the chord (in first inversion, CEGA), the perfect fifth (C–G), is the bottom C, the tonic.
Interval cycles
Interval cycle In music, an interval cycle is a collection of pitch classes created from a sequence of the same interval class.Whittall, Arnold. 2008. ''The Cambridge Introduction to Serialism'', p. 273-74. New York: Cambridge University Press. (pbk). In other wo ...
s, "unfold
.e., repeata single recurrent interval in a series that closes with a return to the initial pitch class", and are notated by
George Perle
George Perle (6 May 1915 – 23 January 2009) was an American composer and music theorist. As a composer, his music was largely atonal, using methods similar to the twelve-tone technique of the Second Viennese School. This serialist style, an ...
using the letter "C", for cycle, with an interval-class integer to distinguish the interval. Thus the diminished-seventh chord would be C3 and the augmented triad would be C4. A superscript may be added to distinguish between transpositions, using 0–11 to indicate the lowest pitch class in the cycle.
[ Perle, George (1990). ''The Listening Composer'', p. 21. California: University of California Press. .]
Alternative interval naming conventions
As shown below, some of the above-mentioned intervals have alternative names, and some of them take a specific alternative name in
Pythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2.Bruce Benward and Marilyn Nadine Saker (2003). ''Music: In Theory and Practice'', seventh edition, 2 vols. (Boston: Mc ...
,
five-limit tuning
Five-limit tuning, 5-limit tuning, or 5-prime-limit tuning (not to be confused with 5-odd-limit tuning), is any system for tuning a musical instrument that obtains the frequency of each note by multiplying the frequency of a given reference note ...
, or meantone temperament tuning systems such as
quarter-comma meantone
Quarter-comma meantone, or -comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. In this system the perfect fifth is flattened by one quarter of a syntonic comma (81:80 ...
. All the intervals with prefix ''sesqui-'' are
justly tuned, and their
frequency ratio
In music, an interval ratio is a ratio of the frequencies of the pitches in a musical interval. For example, a just perfect fifth (for example C to G) is 3:2 (), 1.5, and may be approximated by an equal tempered perfect fifth () which is 27 ...
, shown in the table, is a
superparticular number
In mathematics, a superparticular ratio, also called a superparticular number or epimoric ratio, is the ratio of two consecutive integer numbers.
More particularly, the ratio takes the form:
:\frac = 1 + \frac where is a positive integer.
Th ...
(or epimoric ratio). The same is true for the octave.
Typically, a
comma
The comma is a punctuation mark that appears in several variants in different languages. It has the same shape as an apostrophe or single closing quotation mark () in many typefaces, but it differs from them in being placed on the baseline ...
is a diminished second, but this is not always true (for more details, see
Alternative definitions of comma). For instance, in
Pythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2.Bruce Benward and Marilyn Nadine Saker (2003). ''Music: In Theory and Practice'', seventh edition, 2 vols. (Boston: Mc ...
the diminished second is a descending interval (524288:531441, or about −23.5 cents), and the
Pythagorean comma
In musical tuning, the Pythagorean comma (or ditonic comma), named after the ancient mathematician and philosopher Pythagoras, is the small interval (or comma) existing in Pythagorean tuning between two enharmonically equivalent notes such as C ...
is its opposite (531441:524288, or about 23.5 cents). 5-limit tuning defines
four kinds of comma, three of which meet the definition of diminished second, and hence are listed in the table below. The fourth one, called
syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the Didymean comma, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80 (= 1.0125) ( ...
(81:80) can neither be regarded as a diminished second, nor as its opposite. See
Diminished seconds in 5-limit tuning for further details.
Additionally, some cultures around the world have their own names for intervals found in their music. For instance, 22 kinds of intervals, called
shrutis, are canonically defined in
Indian classical music
Indian classical music is the classical music of the Indian subcontinent. It has two major traditions: the North Indian classical music known as '' Hindustani'' and the South Indian expression known as '' Carnatic''. These traditions were not ...
.
Latin nomenclature
Up to the end of the 18th century,
Latin
Latin (, or , ) is a classical language belonging to the Italic branch of the Indo-European languages. Latin was originally a dialect spoken in the lower Tiber area (then known as Latium) around present-day Rome, but through the power of the ...
was used as an official language throughout Europe for scientific and music textbooks. In music, many English terms are derived from Latin. For instance,
semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically.
It is defined as the interval between two adjacent no ...
is from Latin '.
The prefix semi- is typically used herein to mean "shorter", rather than "half". Namely, a semitonus, semiditonus, semidiatessaron, semidiapente, semihexachordum, semiheptachordum, or semidiapason, is shorter by one semitone than the corresponding whole interval. For instance, a semiditonus (3 semitones, or about 300 cents) is not half of a ditonus (4 semitones, or about 400 cents), but a ditonus shortened by one semitone. Moreover, in
Pythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2.Bruce Benward and Marilyn Nadine Saker (2003). ''Music: In Theory and Practice'', seventh edition, 2 vols. (Boston: Mc ...
(the most commonly used tuning system up to the 16th century), a semitritonus (d5) is smaller than a tritonus (A4) by one
Pythagorean comma
In musical tuning, the Pythagorean comma (or ditonic comma), named after the ancient mathematician and philosopher Pythagoras, is the small interval (or comma) existing in Pythagorean tuning between two enharmonically equivalent notes such as C ...
(about a quarter of a semitone).
Non-diatonic intervals
Intervals in non-diatonic scales can be named using analogs of the diatonic interval names, by using a diatonic interval of similar size and distinguishing it by varying the quality, or by adding other modifiers. For example, the just interval 7/6 may be referred to as a ''subminor third'', since it is ~267 cents wide, which is narrower than a minor third (300 cents in 12-TET, ~316 cents for the just interval 6/5), or as the ''
septimal minor third
In music, the septimal minor third, also called the subminor third (e.g., by Ellis), is the musical interval exactly or approximately equal to a 7/6 ratio of frequencies. In terms of cents, it is 267 cents, a quartertone of size 36/35 flatter ...
'', since it is a
7-limit
7-limit or septimal tunings and intervals are musical instrument tunings that have a limit of seven: the largest prime factor contained in the interval ratios between pitches is seven. Thus, for example, 50:49 is a 7-limit interval, but 14:11 ...
interval. These names refer just to the individual interval's size, and the interval number need not correspond to the number of scale degrees of a (heptatonic) scale. This naming is particularly common in
just intonation
In music, just intonation or pure intonation is the tuning of musical intervals
Interval may refer to:
Mathematics and physics
* Interval (mathematics), a range of numbers
** Partially ordered set#Intervals, its generalization from numbers to ...
and
microtonal
Microtonal music or microtonality is the use in music of microtones—intervals smaller than a semitone, also called "microintervals". It may also be extended to include any music using intervals not found in the customary Western tuning of tw ...
scales.
The most common of these extended qualities are a
neutral interval, in between a minor and major interval; and
subminor and supermajor intervals, respectively narrower than a minor or wider than a major interval. The exact size of such intervals depends on the tuning system, but they often vary from the diatonic interval sizes by about a
quarter tone
A quarter tone is a pitch halfway between the usual notes of a chromatic scale or an interval about half as wide (aurally, or logarithmically) as a semitone, which itself is half a whole tone. Quarter tones divide the octave by 50 cents each, a ...
(50 cents, half a chromatic step). For example, the
neutral second
In music theory, a neutral interval is an interval that is neither a major nor minor, but instead in between. For example, in equal temperament, a major third is 400 cents, a minor third is 300 cents, and a neutral third is 350 cents. A neutral ...
, the characteristic interval of
Arabic music
Arabic music or Arab music ( ar, الموسيقى العربية, al-mūsīqā al-ʿArabīyyah) is the music of the Arab world with all its diverse music styles and genres. Arabic countries have many rich and varied styles of music and also man ...
, in 24-TET is 150 cents, exactly halfway between a minor second and major second. Combined, these yield the progression ''diminished, subminor, minor, neutral, major, supermajor, augmented'' for seconds, thirds, sixths, and sevenths. This naming convention can be extended to unisons, fourths, fifths, and octaves with ''sub'' and ''super'', yielding the progression ''diminished, sub, perfect, super, augmented''. This allows one to name all intervals in 24-TET or 31-TET, the latter of which was used by
Adriaan Fokker
Adriaan Daniël Fokker (; 17 August 1887 – 24 September 1972) was a Dutch physicist. He worked in the fields of special relativity and statistical mechanics. He was the inventor of the Fokker organ, a 31-tone equal-tempered (31-TET) organ. ...
. Various further extensions are used in
Xenharmonic music
Xenharmonic music is music that uses a tuning system that is unlike the 12-tone equal temperament scale. It was named by Ivor Darreg, from Xenia (Greek ξενία), ''hospitable,'' and Xenos (Greek ξένος) ''foreign.'' He stated that it was ...
.
Pitch-class intervals
In post-tonal or
atonal
Atonality in its broadest sense is music that lacks a tonal center, or key. ''Atonality'', in this sense, usually describes compositions written from about the early 20th-century to the present day, where a hierarchy of harmonies focusing on a s ...
theory, originally developed for equal-tempered European classical music written using the
twelve-tone technique
The twelve-tone technique—also known as dodecaphony, twelve-tone serialism, and (in British usage) twelve-note composition—is a method of musical composition first devised by Austrian composer Josef Matthias Hauer, who published his "law o ...
or
serialism
In music, serialism is a method of Musical composition, composition using series of pitches, rhythms, dynamics, timbres or other elements of music, musical elements. Serialism began primarily with Arnold Schoenberg's twelve-tone technique, thou ...
,
integer notation
In music, a pitch class (p.c. or pc) is a set of all pitches that are a whole number of octaves apart; for example, the pitch class C consists of the Cs in all octaves. "The pitch class C stands for all possible Cs, in whatever octave positio ...
is often used, most prominently in
musical set theory
Musical set theory provides concepts for categorizing musical objects and describing their relationships. Howard Hanson first elaborated many of the concepts for analyzing tonal music. Other theorists, such as Allen Forte, further developed the ...
. In this system, intervals are named according to the number of half steps, from 0 to 11, the largest interval class being 6.
In atonal or musical set theory, there are numerous types of intervals, the first being the
ordered pitch interval
In musical set theory, a pitch interval (PI or ip) is the number of semitones that separates one pitch from another, upward or downward.Schuijer, Michiel (2008). ''Analyzing Atonal Music: Pitch-Class Set Theory and Its Contexts'', Eastman Studie ...
, the distance between two pitches upward or downward. For instance, the interval from C upward to G is 7, and the interval from G downward to C is −7. One can also measure the distance between two pitches without taking into account direction with the unordered pitch interval, somewhat similar to the interval of tonal theory.
The interval between pitch classes may be measured with ordered and unordered pitch-class intervals. The ordered one, also called directed interval, may be considered the measure upwards, which, since we are dealing with pitch classes, depends on whichever pitch is chosen as 0. For unordered pitch-class intervals, see
interval class
In musical set theory, an interval class (often abbreviated: ic), also known as unordered pitch-class interval, interval distance, undirected interval, or "(even completely incorrectly) as 'interval mod 6'" (; ), is the shortest distance in pitch ...
.
Generic and specific intervals
In
diatonic set theory
Diatonic set theory is a subdivision or application of musical set theory which applies the techniques and analysis of discrete mathematics to properties of the diatonic collection such as maximal evenness, Myhill's property, well formedness, th ...
,
specific
Specific may refer to:
* Specificity (disambiguation)
* Specific, a cure or therapy for a specific illness
Law
* Specific deterrence, focussed on an individual
* Specific finding, intermediate verdict used by a jury in determining the fina ...
and
generic interval
In diatonic set theory a generic interval is the number of scale steps between notes of a collection or scale. The largest generic interval is one less than the number of scale members. (Johnson 2003, p. 26)
A specific interval is the cl ...
s are distinguished. Specific intervals are the interval class or number of semitones between scale steps or collection members, and generic intervals are the number of diatonic scale steps (or staff positions) between notes of a collection or scale.
Notice that staff positions, when used to determine the conventional interval number (second, third, fourth, etc.), are counted including the position of the lower note of the interval, while generic interval numbers are counted excluding that position. Thus, generic interval numbers are smaller by 1, with respect to the conventional interval numbers.
Comparison
Generalizations and non-pitch uses

The term "interval" can also be generalized to other music elements besides pitch.
David Lewin
David Benjamin Lewin (July 2, 1933 – May 5, 2003) was an American music theorist, music critic and composer. Called "the most original and far-ranging theorist of his generation", he did his most influential theoretical work on the development of ...
's ''Generalized Musical Intervals and Transformations'' uses interval as a generic measure of distance between
time point
In music a time point or ''timepoint'' ( point in time) is "an instant, analogous to a geometrical point in space". Because it has no duration, it literally cannot be heard, but it may be used to represent "the point of initiation of a single pit ...
s,
timbre
In music, timbre ( ), also known as tone color or tone quality (from psychoacoustics), is the perceived sound quality of a musical note, sound or musical tone, tone. Timbre distinguishes different types of sound production, such as choir voice ...
s, or more abstract musical phenomena.
[Ockelford, Adam (2005). ''Repetition in Music: Theoretical and Metatheoretical Perspectives'', p. 7. . "Lewin posits the notion of musical 'spaces' made up of elements between which we can intuit 'intervals'....Lewin gives a number of examples of musical spaces, including the diatonic gamut of pitches arranged in scalar order; the 12 pitch classes under equal temperament; a succession of time-points pulsing at regular temporal distances one time unit apart; and a family of durations, each measuring a temporal span in time units....transformations of timbre are proposed that derive from changes in the spectrum of partials..."]
For example, an interval between two bell-like sounds, which have no pitch salience, is still perceptible. When two tones have similar acoustic spectra (sets of partials), the interval is just the distance of the shift of a tone spectrum along the frequency axis, so linking to pitches as reference points is not necessary. The same principle naturally applies to pitched tones (with similar harmonic spectra), which means that intervals can be perceived "directly" without pitch recognition. This explains in particular the predominance of interval hearing over absolute pitch hearing.
See also
*
Circle of fifths
In music theory, the circle of fifths is a way of organizing the 12 chromatic pitches as a sequence of perfect fifths. (This is strictly true in the standard 12-tone equal temperament system — using a different system requires one interval ...
*
Ear training
Ear training or aural skills is a music theory study in which musicians learn to identify pitches, intervals, melody, chords, rhythms, solfeges, and other basic elements of music, solely by hearing. The application of this skill is analogous t ...
*
List of meantone intervals
The following is a list of intervals of extended meantone temperament. These intervals constitute the standard vocabulary of intervals for the Western common practice era. Here 12-EDO refers to the size of the interval in 12 equal divisions of th ...
*
List of pitch intervals
Below is a list of intervals expressible in terms of a prime limit (see Terminology), completed by a choice of intervals in various equal subdivisions of the octave or of other intervals.
For commonly encountered harmonic or melodic intervals ...
*
Music and mathematics
Music theory analyzes the pitch, timing, and structure of music. It uses mathematics to study elements of music such as tempo, chord progression, form, and meter. The attempt to structure and communicate new ways of composing and hearing mus ...
*
Pseudo-octave
A pseudo-octave, pseudooctave,"Interview with Max Mathews", p.21. Author(s): C. Roads and Max Mathews. Source: ''Computer Music Journal'', Vol. 4, No. 4, (Winter, 1980), pp. 15–22. Published by: The MIT Press. or paradoxical octave"The Parado ...
*
Regular temperament
Regular temperament is any tempered system of musical tuning such that each frequency ratio is obtainable as a product of powers of a finite number of generators, or generating frequency ratios. For instance, in 12-TET, the system of music most ...
Notes
References
External links
* Gardner, Carl E. (1912)
''Essentials of Music Theory'' p. 38
"Interval" ''
Encyclopædia Britannica
The (Latin for "British Encyclopædia") is a general knowledge English-language encyclopaedia. It is published by Encyclopædia Britannica, Inc.; the company has existed since the 18th century, although it has changed ownership various time ...
''
Lissajous Curves: Interactive simulation of graphical representations of musical intervals, beats, interference, vibrating stringsElements of Harmony: Vertical Intervals*
{{DEFAULTSORT:Interval
 In Western
In Western  The name of any interval is further qualified using the terms perfect (P),
The name of any interval is further qualified using the terms perfect (P),  The distinction between diatonic and chromatic intervals may be also sensitive to context. The above-mentioned 56 intervals formed by the C-major scale are sometimes called ''diatonic to C major''. All other intervals are called ''chromatic to C major''. For instance, the perfect fifth A–E is chromatic to C major, because A and E are not contained in the C major scale. However, it is diatonic to others, such as the A major scale.
The distinction between diatonic and chromatic intervals may be also sensitive to context. The above-mentioned 56 intervals formed by the C-major scale are sometimes called ''diatonic to C major''. All other intervals are called ''chromatic to C major''. For instance, the perfect fifth A–E is chromatic to C major, because A and E are not contained in the C major scale. However, it is diatonic to others, such as the A major scale.
 A simple interval is an interval spanning at most one octave (see Main intervals above). Intervals spanning more than one octave are called compound intervals, as they can be obtained by adding one or more octaves to a simple interval (see
A simple interval is an interval spanning at most one octave (see Main intervals above). Intervals spanning more than one octave are called compound intervals, as they can be obtained by adding one or more octaves to a simple interval (see 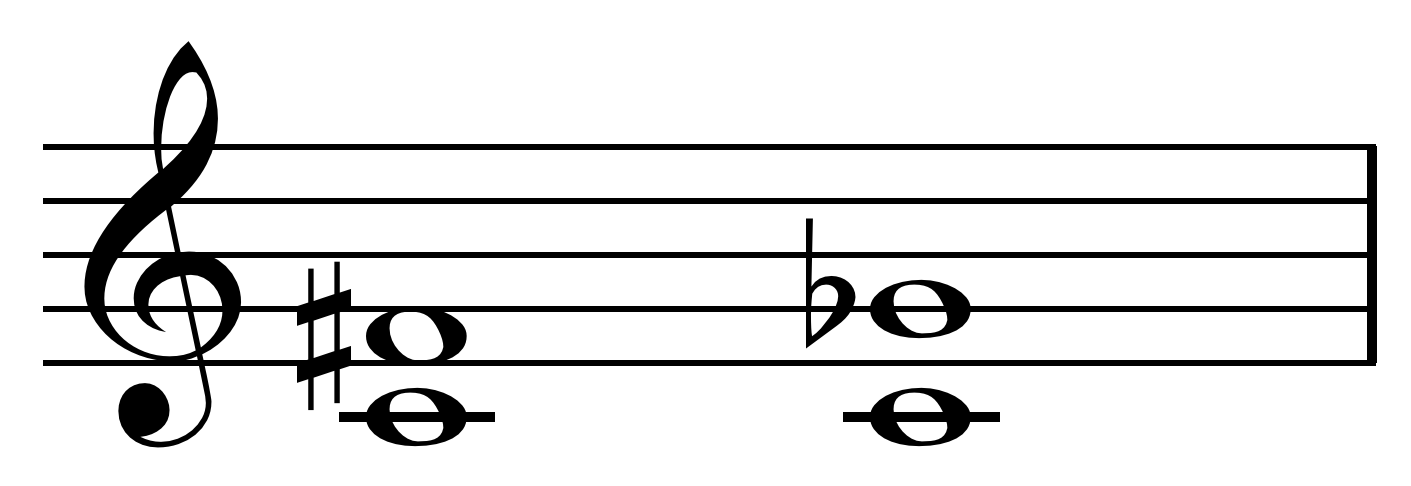 Two intervals are considered ''
Two intervals are considered '' There are also a number of minute intervals not found in the chromatic scale or labeled with a diatonic function, which have names of their own. They may be described as microtones, and some of them can be also classified as
There are also a number of minute intervals not found in the chromatic scale or labeled with a diatonic function, which have names of their own. They may be described as microtones, and some of them can be also classified as  A compound interval is an interval spanning more than one octave. Conversely, intervals spanning at most one octave are called simple intervals (see Main intervals below).
In general, a compound interval may be defined by a sequence or "stack" of two or more simple intervals of any kind. For instance, a major tenth (two staff positions above one octave), also called ''compound major third'', spans one octave plus one major third.
Any compound interval can be always decomposed into one or more octaves plus one simple interval. For instance, a major seventeenth can be decomposed into two octaves and one major third, and this is the reason why it is called a compound major third, even when it is built by adding up four fifths.
The diatonic number ''DN''c of a compound interval formed from ''n'' simple intervals with diatonic numbers ''DN''1, ''DN''2, ..., ''DN''n, is determined by:
:
which can also be written as:
:
The quality of a compound interval is determined by the quality of the simple interval on which it is based. For instance, a compound major third is a major tenth (1+(8−1)+(3−1) = 10), or a major seventeenth (1+(8−1)+(8−1)+(3−1) = 17), and a compound perfect fifth is a perfect twelfth (1+(8−1)+(5−1) = 12) or a perfect nineteenth (1+(8−1)+(8−1)+(5−1) = 19). Notice that two octaves are a fifteenth, not a sixteenth (1+(8−1)+(8−1) = 15). Similarly, three octaves are a twenty-second (1+3×(8−1) = 22), and so on.
A compound interval is an interval spanning more than one octave. Conversely, intervals spanning at most one octave are called simple intervals (see Main intervals below).
In general, a compound interval may be defined by a sequence or "stack" of two or more simple intervals of any kind. For instance, a major tenth (two staff positions above one octave), also called ''compound major third'', spans one octave plus one major third.
Any compound interval can be always decomposed into one or more octaves plus one simple interval. For instance, a major seventeenth can be decomposed into two octaves and one major third, and this is the reason why it is called a compound major third, even when it is built by adding up four fifths.
The diatonic number ''DN''c of a compound interval formed from ''n'' simple intervals with diatonic numbers ''DN''1, ''DN''2, ..., ''DN''n, is determined by:
:
which can also be written as:
:
The quality of a compound interval is determined by the quality of the simple interval on which it is based. For instance, a compound major third is a major tenth (1+(8−1)+(3−1) = 10), or a major seventeenth (1+(8−1)+(8−1)+(3−1) = 17), and a compound perfect fifth is a perfect twelfth (1+(8−1)+(5−1) = 12) or a perfect nineteenth (1+(8−1)+(8−1)+(5−1) = 19). Notice that two octaves are a fifteenth, not a sixteenth (1+(8−1)+(8−1) = 15). Similarly, three octaves are a twenty-second (1+3×(8−1) = 22), and so on.
 The term "interval" can also be generalized to other music elements besides pitch.
The term "interval" can also be generalized to other music elements besides pitch.