|
Ditone
In music, a ditone (, from , "of two tones") is the interval of a major third. The size of a ditone varies according to the sizes of the two tones of which it is compounded. The largest is the Pythagorean ditone, with a ratio of 81:64, also called a comma-redundant major third; the smallest is the interval with a ratio of 100:81, also called a comma-deficient major third. Pythagorean tuning The Pythagorean ditone is the major third in Pythagorean tuning, which has an interval ratio of 81:64, which is 407.82 cents. The Pythagorean ditone is evenly divisible by two major tones (9/8 or 203.91 cents) and is wider than a just major third (5/4, 386.31 cents) by a syntonic comma (81/80, 21.51 cents). Because it is a comma wider than a "perfect" major third of 5:4, it is called a "comma-redundant" interval. "The major third that appears commonly in the ythagoreansystem (C–E, D–F, etc.) is more properly known as the Pythagorean ditone and consists of two major and two minor semit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
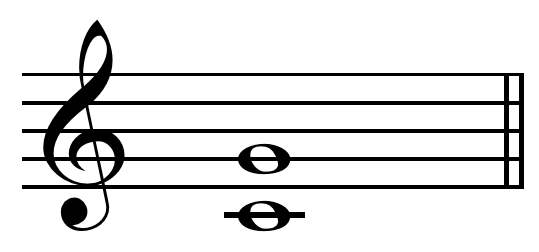
Ditone On C
In music, a ditone (, from , "of two tones") is the interval of a major third. The size of a ditone varies according to the sizes of the two tones of which it is compounded. The largest is the Pythagorean ditone, with a ratio of 81:64, also called a comma-redundant major third; the smallest is the interval with a ratio of 100:81, also called a comma-deficient major third. Pythagorean tuning The Pythagorean ditone is the major third in Pythagorean tuning, which has an interval ratio of 81:64, which is 407.82 cents. The Pythagorean ditone is evenly divisible by two major tones (9/8 or 203.91 cents) and is wider than a just major third (5/4, 386.31 cents) by a syntonic comma (81/80, 21.51 cents). Because it is a comma wider than a "perfect" major third of 5:4, it is called a "comma-redundant" interval. "The major third that appears commonly in the ythagoreansystem (C–E, D–F, etc.) is more properly known as the Pythagorean ditone and consists of two major and two minor sem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Interval
In musical tuning theory, a Pythagorean interval is a musical interval with frequency ratio equal to a power of two divided by a power of three, or vice versa.Benson, Donald C. (2003). ''A Smoother Pebble: Mathematical Explorations'', p.56. . "The frequency ratio of every Pythagorean interval is a ratio between a power of two and a power of three...confirming the Pythagorean requirements that all intervals be associated with ratios of whole numbers." For instance, the perfect fifth with ratio 3/2 (equivalent to 31/ 21) and the perfect fourth with ratio 4/3 (equivalent to 22/ 31) are Pythagorean intervals. All the intervals between the notes of a scale are Pythagorean if they are tuned using the Pythagorean tuning system. However, some Pythagorean intervals are also used in other tuning systems. For instance, the above-mentioned Pythagorean perfect fifth and fourth are also used in just intonation. Interval table Notice that the terms ''ditone'' and ''semiditone'' are specific ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3-limit Tuning And Intervals
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2.Bruce Benward and Marilyn Nadine Saker (2003). ''Music: In Theory and Practice'', seventh edition, 2 vols. (Boston: McGraw-Hill). Vol. I: p. 56. . This ratio, also known as the " pure" perfect fifth, is chosen because it is one of the most consonant and easiest to tune by ear and because of importance attributed to the integer 3. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2 (i.e., the untempered perfect fifth), which is ≈702 cents wide. The system dates to Ancient Mesopotamia; see . The system is named, and has been widely misattributed, to Ancient Greeks, notably Pythagoras (sixth century BC) by modern authors of music theory, while Ptolemy, and later Boethius, ascribed the di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Tuning
Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2.Bruce Benward and Marilyn Nadine Saker (2003). ''Music: In Theory and Practice'', seventh edition, 2 vols. (Boston: McGraw-Hill). Vol. I: p. 56. . This ratio, also known as the " pure" perfect fifth, is chosen because it is one of the most consonant and easiest to tune by ear and because of importance attributed to the integer 3. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2 (i.e., the untempered perfect fifth), which is ≈702 cents wide. The system dates to Ancient Mesopotamia; see . The system is named, and has been widely misattributed, to Ancient Greeks, notably Pythagoras (sixth century BC) by modern authors of music theory, while Ptolemy, and later Boethius, ascribed the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Third
In classical music, a third is a musical interval encompassing three staff positions (see Interval number for more details), and the major third () is a third spanning four semitones. Forte, Allen (1979). ''Tonal Harmony in Concept and Practice'', p.8. Holt, Rinehart, and Winston. Third edition . "A large 3rd, or ''major 3rd'' (M3) encompassing four half steps." Along with the minor third, the major third is one of two commonly occurring thirds. It is qualified as ''major'' because it is the larger of the two: the major third spans four semitones, the minor third three. For example, the interval from C to E is a major third, as the note E lies four semitones above C, and there are three staff positions from C to E. Diminished and augmented thirds span the same number of staff positions, but consist of a different number of semitones (two and five). The major third may be derived from the harmonic series as the interval between the fourth and fifth harmonics. The maj ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Whole Tone
In Western music theory, a major second (sometimes also called whole tone or a whole step) is a second spanning two semitones (). A second is a musical interval encompassing two adjacent staff positions (see Interval number for more details). For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff positions. Diminished, minor and augmented seconds are notated on adjacent staff positions as well, but consist of a different number of semitones (zero, one, and three). The major second is the interval that occurs between the first and second degrees of a major scale, the tonic and the supertonic. On a musical keyboard, a major second is the interval between two keys separated by one key, counting white and black keys alike. On a guitar string, it is the interval separated by two frets. In moveable-do solfège, it is the interval between ''do'' and ''re''. It is considered a me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ptolemy's Intense Diatonic Scale
Ptolemy's intense diatonic scale, also known as the Ptolemaic sequence, justly tuned major scale, Ptolemy's tense diatonic scale, or the syntonous (or syntonic) diatonic scale, is a tuning for the diatonic scale proposed by Ptolemy, and corresponding with modern 5-limit just intonation.Chisholm, Hugh (1911). The Encyclopædia Britannica', Vol.28, p. 961. The Encyclopædia Britannica Company. This tuning was declared by Zarlino to be the only tuning that could be reasonably sung, it was also supported by Giuseppe Tartini, and is equivalent to Indian Gandhar tuning which features exactly the same intervals. It is produced through a tetrachord consisting of a greater tone (9:8), lesser tone (10:9), and just diatonic semitone (16:15). This is called Ptolemy's intense diatonic tetrachord (or "tense"), as opposed to Ptolemy's soft diatonic tetrachord (or "relaxed"), which is formed by 21:20, 10:9 and 8:7 intervals. Structure The structure of the intense diatonic scale is shown in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Tone
In Western music theory, a major second (sometimes also called whole tone or a whole step) is a second spanning two semitones (). A second is a musical interval encompassing two adjacent staff positions (see Interval number for more details). For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff positions. Diminished, minor and augmented seconds are notated on adjacent staff positions as well, but consist of a different number of semitones (zero, one, and three). The major second is the interval that occurs between the first and second degrees of a major scale, the tonic and the supertonic. On a musical keyboard, a major second is the interval between two keys separated by one key, counting white and black keys alike. On a guitar string, it is the interval separated by two frets. In moveable-do solfège, it is the interval between ''do'' and ''re''. It is considered a melodi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interval (music)
In music theory, an interval is a difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord. In Western music, intervals are most commonly differences between notes of a diatonic scale. Intervals between successive notes of a scale are also known as scale steps. The smallest of these intervals is a semitone. Intervals smaller than a semitone are called microtones. They can be formed using the notes of various kinds of non-diatonic scales. Some of the very smallest ones are called commas, and describe small discrepancies, observed in some tuning systems, between enharmonically equivalent notes such as C and D. Intervals can be arbitrarily small, and even imperceptible to the human ear. In physical terms, an interval is the ratio between two sonic fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Syntonic Comma
In music theory, the syntonic comma, also known as the chromatic diesis, the Didymean comma, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80 (= 1.0125) (around 21.51 cents). Two notes that differ by this interval would sound different from each other even to untrained ears, , ''BBC''. but would be close enough that they would be more likely interpreted as out-of-tune versions of the same note than as different notes. The comma is also referred to as a Didymean comma because it is the amount by which Didymus corrected the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Major Second
In Western music theory, a major second (sometimes also called whole tone or a whole step) is a second spanning two semitones (). A second is a musical interval encompassing two adjacent staff positions (see Interval number for more details). For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff positions. Diminished, minor and augmented seconds are notated on adjacent staff positions as well, but consist of a different number of semitones (zero, one, and three). The major second is the interval that occurs between the first and second degrees of a major scale, the tonic and the supertonic. On a musical keyboard, a major second is the interval between two keys separated by one key, counting white and black keys alike. On a guitar string, it is the interval separated by two frets. In moveable-do solfège, it is the interval between ''do'' and ''re''. It is considered a me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |