History of mathematical notation on:
[Wikipedia]
[Google]
[Amazon]
The history of mathematical notation includes the commencement, progress, and
 Written mathematics began with numbers expressed as
Written mathematics began with numbers expressed as
 The history of mathematics cannot with certainty be traced back to any school or period before that of the Ionian Greeks, but the subsequent history may be divided into periods, the distinctions between which are tolerably well marked. Greek mathematics, which originated with the study of geometry, tended from its commencement to be deductive and scientific. Since the fourth century AD,
The history of mathematics cannot with certainty be traced back to any school or period before that of the Ionian Greeks, but the subsequent history may be divided into periods, the distinctions between which are tolerably well marked. Greek mathematics, which originated with the study of geometry, tended from its commencement to be deductive and scientific. Since the fourth century AD,  In the historical development of geometry, the steps in the abstraction of geometry were made by the ancient Greeks.
In the historical development of geometry, the steps in the abstraction of geometry were made by the ancient Greeks.
683
/ref> and could be used with tolerable effect as an instrument of calculation, to which purpose the Roman system was totally inapplicable. The Greeks divided the twenty-four letters of their alphabet into three classes, and, by adding another symbol to each class, they had characters to represent the units, tens, and hundreds. (
would be written as:
SS2 C3 x5 M S4 u6
.
 The Chinese used numerals that look much like the tally system. Numbers one through four were horizontal lines. Five was an X between two horizontal lines; it looked almost exactly the same as the
The Chinese used numerals that look much like the tally system. Numbers one through four were horizontal lines. Five was an X between two horizontal lines; it looked almost exactly the same as the 
 The state of
The state of
 Despite their name,
Despite their name,
ImageSize = width:678 height:285
PlotArea = left:65 right:55 bottom:20 top:15
AlignBars = justify
Colors =
id:time value:rgb(0.7,0.7,1) #
id:period value:rgb(1,0.7,0.5) #
id:age value:rgb(0.95,0.85,0.5) #
id:era value:rgb(1,0.85,0.5) #
id:eon value:rgb(1,0.85,0.7) #
id:filler value:gray(0.8) # background bar
id:black value:black
Period = from:1360 till:1962
TimeAxis = orientation:horizontal
ScaleMajor = unit:year increment:100 start:1360
ScaleMinor = unit:year increment:10 start:1360
PlotData =
align:center textcolor:black fontsize:8 mark:(line,black) width:15
bar: color:filler width:15
from:1360 till:1962 shift:(0,10) text: Symbolic Notation
from:1360 till:1704 shift:(-40,0) text:Early
from:1704 till:1876 text:High
from:1876 till:1962 text:Late
bar: color:age width:5
from:1360 till:1618 shift:(0,-10) text:Arithmetic
from:1618 till:1718 shift:(0,-10) text:Multiplication
from:1718 till:1846 shift:(0,-10) text:Division
from:1846 till:1962 shift:(10,-10) text:Abstraction
mark:(line,black) textcolor:black fontsize:M
bar:Events color:filler align:left
at:1360 shift:(2,0) text:"
 The 14th century saw the development of new mathematical concepts to investigate a wide range of problems. The two widely used arithmetic symbols are addition and subtraction, + and −. The plus sign was used by 1360 by Nicole OresmeHis own personal use started around 1351. in his work ''Algorismus proportionum''. It is thought an abbreviation for "et", meaning "and" in Latin, in much the same way the ampersand sign also began as "et". Oresme at the University of Paris and the Italian Giovanni di Casali independently provided graphical demonstrations of the distance covered by a body undergoing uniformly accelerated motion, asserting that the area under the line depicting the constant acceleration and represented the total distance traveled. The minus sign was used in 1489 by Johannes Widmann in ''Mercantile Arithmetic'' or ''Behende und hüpsche Rechenung auff allen Kauffmanschafft,''. Widmann used the minus symbol with the plus symbol, to indicate deficit and surplus, respectively. In ''Summa de arithmetica, Summa de arithmetica, geometria, proportioni e proportionalità'',Summa de Arithmetica: Geometria Proportioni et Proportionalita. ''Tr''. Sum of Arithmetic: Geometry in proportions and proportionality. Luca Pacioli used symbols for plus and minus symbols and contained
The 14th century saw the development of new mathematical concepts to investigate a wide range of problems. The two widely used arithmetic symbols are addition and subtraction, + and −. The plus sign was used by 1360 by Nicole OresmeHis own personal use started around 1351. in his work ''Algorismus proportionum''. It is thought an abbreviation for "et", meaning "and" in Latin, in much the same way the ampersand sign also began as "et". Oresme at the University of Paris and the Italian Giovanni di Casali independently provided graphical demonstrations of the distance covered by a body undergoing uniformly accelerated motion, asserting that the area under the line depicting the constant acceleration and represented the total distance traveled. The minus sign was used in 1489 by Johannes Widmann in ''Mercantile Arithmetic'' or ''Behende und hüpsche Rechenung auff allen Kauffmanschafft,''. Widmann used the minus symbol with the plus symbol, to indicate deficit and surplus, respectively. In ''Summa de arithmetica, Summa de arithmetica, geometria, proportioni e proportionalità'',Summa de Arithmetica: Geometria Proportioni et Proportionalita. ''Tr''. Sum of Arithmetic: Geometry in proportions and proportionality. Luca Pacioli used symbols for plus and minus symbols and contained
which can be viewed as a version of the
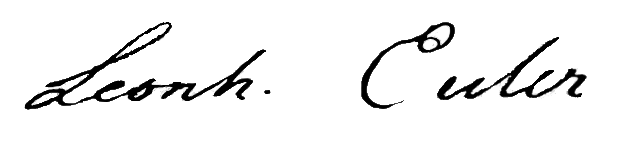 Leonhard Euler was one of the most prolific mathematicians in history, and also a prolific inventor of canonical notation. Contributions of Leonhard Euler to mathematics, His contributions include his use of ''e (mathematical constant), e'' to represent the base of natural logarithms. It is not known exactly why was chosen, but it was probably because the four letters of the alphabet were already commonly used to represent variables and other constants. Euler used to represent pi consistently. The use of was suggested by William Jones (mathematician), William Jones, who used it as shorthand for perimeter. Euler used to represent the square root of negative one,That is, although he earlier used it as an ''infinite number.''Today, the symbol created by John Wallis, , is used for infinity.As in, For
Leonhard Euler was one of the most prolific mathematicians in history, and also a prolific inventor of canonical notation. Contributions of Leonhard Euler to mathematics, His contributions include his use of ''e (mathematical constant), e'' to represent the base of natural logarithms. It is not known exactly why was chosen, but it was probably because the four letters of the alphabet were already commonly used to represent variables and other constants. Euler used to represent pi consistently. The use of was suggested by William Jones (mathematician), William Jones, who used it as shorthand for perimeter. Euler used to represent the square root of negative one,That is, although he earlier used it as an ''infinite number.''Today, the symbol created by John Wallis, , is used for infinity.As in, For
Where, ''i'' represents the ''index of summation''; ''ai'' is an indexed variable representing each successive term in the series; ''m'' is the ''lower bound of summation'', and ''n'' is the ''upper bound of summation''. The ''"i = m"'' under the summation symbol means that the index ''i'' starts out equal to ''m''. The index, ''i'', is incremented by 1 for each successive term, stopping when ''i'' = ''n''. For function (mathematics), functions, Euler used the notation to represent a function of . In 1730, Euler wrote the gamma function.That is, .
valid for n > 0. In 1736, Euler produced his paper on the Seven Bridges of Königsberg initiating the study of graph theory. The William Emerson (mathematician), mathematician William Emerson would develop the proportionality sign.That is,
where
and, in 1849, coquaternions. In 1848, James Joseph Sylvester introduced into matrix algebra the term Matrix (mathematics), matrix.This is Latin for "womb".
 In 1864 James Clerk Maxwell reduced all of the then current knowledge of electromagnetism into a linked set of differential equations with 20 equations in 20 variables, contained in ''A Dynamical Theory of the Electromagnetic Field''. (This article accompanied an 8 December 1864 presentation by Maxwell to the Royal Society.) (See Maxwell's equations.) The method of calculation which it is necessary to employ was given by Lagrange, and afterwards developed, with some modifications, by Hamilton's equations. It is usually referred to as Hamilton's principle; when the equations in the original form are used they are known as Lagrange's equations. In 1871 Richard Dedekind called a set of real or complex numbers which is closed under the four arithmetic operations a field (mathematics), field. In 1873 Maxwell presented ''A Treatise on Electricity and Magnetism''.
In 1878, William Kingdon Clifford published his Elements of Dynamic. Clifford developed split-biquaternions,That is, History of quaternions, which he called ''algebraic motors''. Clifford obviated quaternion study by separating the
In 1864 James Clerk Maxwell reduced all of the then current knowledge of electromagnetism into a linked set of differential equations with 20 equations in 20 variables, contained in ''A Dynamical Theory of the Electromagnetic Field''. (This article accompanied an 8 December 1864 presentation by Maxwell to the Royal Society.) (See Maxwell's equations.) The method of calculation which it is necessary to employ was given by Lagrange, and afterwards developed, with some modifications, by Hamilton's equations. It is usually referred to as Hamilton's principle; when the equations in the original form are used they are known as Lagrange's equations. In 1871 Richard Dedekind called a set of real or complex numbers which is closed under the four arithmetic operations a field (mathematics), field. In 1873 Maxwell presented ''A Treatise on Electricity and Magnetism''.
In 1878, William Kingdon Clifford published his Elements of Dynamic. Clifford developed split-biquaternions,That is, History of quaternions, which he called ''algebraic motors''. Clifford obviated quaternion study by separating the
''Theory and Calculation of Transient Electric Phenomena and Oscillations''
 Albert Einstein, in 1916, introduced the Einstein notationThe indices range over Set (mathematics), set ,
Albert Einstein, in 1916, introduced the Einstein notationThe indices range over Set (mathematics), set ,
is reduced by the convention to:
Upper indices are not Exponentiation, exponents but are indices of coordinates,
See also: Ricci calculus which summed over a set of index notation, indexed terms in a formula, thus exerting notational brevity. Arnold Sommerfeld would create the contour integral sign in 1917. Also in 1917, Dimitry Mirimanoff proposes axiom of regularity. In 1919, Theodor Kaluza would solve general relativity equations using Five-dimensional space, five dimensions, the results would have electromagnetic equations emerge. This would be published in 1921 in "Zum Unitätsproblem der Physik". In 1922, Abraham Fraenkel and Thoralf Skolem independently proposed replacing the axiom schema of specification with the axiom schema of replacement. Also in 1922, Zermelo–Fraenkel set theory was developed. In 1923, Steinmetz would publis
''Four Lectures on Relativity and Space''
Around 1924, Jan Arnoldus Schouten would develop the modern notation and formalism for the Ricci calculus framework during the absolute differential calculus applications to general relativity and differential geometry in the early twentieth century.Ricci calculus constitutes the rules of index notation and manipulation for tensors and tensor fields. See also: In 1925, Enrico Fermi would describe a Fermi–Dirac statistics, system comprising many identical particles that obey the Pauli exclusion principle, afterwards developing a diffusion equation (Fermi age equation). In 1926, Oskar Klein would develop the Kaluza–Klein theory. In 1928, Emil Artin abstracted ring theory with Artinian rings. In 1933, Andrey Kolmogorov introduces the ''Kolmogorov axioms''. In 1937, Bruno de Finetti deduced the "Coherence (philosophical gambling strategy), operational subjective" concept.
A ''constant'', in a mathematical context, is a Mathematical constant, number that arises naturally in mathematics, such as π or e; Such constant (mathematics), mathematics constant value do not change. It can mean polynomial constant term (the term of degree 0) or the constant of integration, a free parameter arising in integration.
Related, the physical constant are a physical quantity generally believed to be universal and unchanging. Constant (programming), Programming constants are a values that, unlike a variable, cannot be reassociated with a different value. and logical operators. The corresponding logical operations are known, respectively, as logical conjunction, conjunction,
Here a symbols that represents a quantity in a mathematical expression, a Variable (mathematics), mathematical variable as used in many sciences.
Variables can be symbolic name associated with a value and whose associated value may be changed, known in computer science as a Variable (computer science), variable reference. A ''variable'' can also be the operationalization, operationalized way in which the attribute is represented for further data processing (e.g., a logical set of attributes). See also: Dependent and independent variables in statistics. and by sentences containing variables, called Predicate (mathematical logic), predicates.Usually denoted by an uppercase letter followed by a list of variables, such as P(''x'') or Q(''y'',''z'')
Here a Predicate (mathematical logic), mathematical logic predicate, a fundamental concept in first-order logic. Predicate (grammar), Grammatical predicates are grammatical components of a sentence.
Related is the syntactic predicate in parser technology which are guidelines for the parser process. In computer programming, a branch predication allows a choice to execute or not to execute a given instruction based on the content of a machine register. In addition, predicate logic allows Quantifiers (logic), quantifiers.Representing ALL and EXISTS With these logic symbols and additional Quantifier (logic), quantifiers from predicate logic,e.g. ∃ for "there exists" and ∀ for "for all" Validity (logic), valid Mathematical proof, proofs Argumentation theory#Mathematical argumentation, can be made that are Absurdity, irrationally artificial,See also: Dialetheism, Contradiction, and Paradox but syntactical.Related, dict:facetious, facetious abstract nonsense describes certain kinds of arguments and methods related to category theory which resembles comical Non sequitur (literary device), literary non-sequitur devices (not Non sequitur (logic), illogical non-sequiturs).
If the Gödel numbers replace the symbols, it becomes:.
There are ten numbers, so the ten prime numbers are found and these are: .
Then, the Gödel numbers are made the powers of the respective primes and multiplied, giving: .
The resulting number is approximately .
The first formulation of a quantum mechanics, quantum theory describing radiation and matter interaction is due to Paul Adrien Maurice Dirac, who, during 1920, was first able to compute the coefficient of spontaneous emission of an atom. In 1928, the relativistic wave equation, relativistic Dirac equation was formulated by Dirac to explain the behavior of the relativistically moving electron.The Dirac equation in the form originally proposed by Dirac is:
where, is the wave function for the electron, and are the space and time coordinates, is the rest mass of the electron, is the momentum, understood to be the momentum operator in the Schrödinger equation, Schrödinger theory, is the speed of light, and is the reduced Planck constant. Dirac described the quantification of the electromagnetic field as an ensemble of harmonic oscillators with the introduction of the concept of creation and annihilation operators of particles. In the following years, with contributions from Wolfgang Pauli, Eugene Wigner, Pascual Jordan, and Werner Heisenberg, and an elegant formulation of quantum electrodynamics due to Enrico Fermi, physicists came to believe that, in principle, it would be possible to perform any computation for any physical process involving photons and charged particles. In 1931, Alexandru Proca developed the Proca equation (Euler–Lagrange equation)That is,
for the vector meson theory of nuclear forces and the relativistic quantum field equations. John Archibald Wheeler in 1937 develops S-matrix. Studies by Felix Bloch with Arnold Nordsieck, and Victor Weisskopf, in 1937 and 1939, revealed that such computations were reliable only at a first order of Perturbation theory (quantum mechanics), perturbation theory, a problem already pointed out by Robert Oppenheimer. At higher orders in the series infinities emerged, making such computations meaningless and casting serious doubts on the internal consistency of the theory itself. With no solution for this problem known at the time, it appeared that a fundamental incompatibility existed between special relativity and quantum mechanics. In the 1930s, the double-struck capital Z for integer number sets was created by Edmund Landau. Nicolas Bourbaki created the double-struck capital Q for rational number sets. In 1935, Gerhard Gentzen made universal quantifiers. In 1936, Tarski's undefinability theorem is stated by Alfred Tarski and proved.The theorem applies more generally to any sufficiently strong formal system, showing that truth in the standard model of the system cannot be defined within the system. In 1938, Kurt Gödel, Gödel proposes the constructible universe in the paper "
The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis
'". André Weil and Nicolas Bourbaki would develop the empty set sign in 1939. That same year, Nathan Jacobson would coin the double-struck capital C for complex number sets. Around the 1930s, Voigt notationNamed to honor Voigt's 1898 work. would be developed for multilinear algebra as a way to represent a symmetric tensor by reducing its order. Schoenflies notation, Schönflies notationNamed after Arthur Moritz Schoenflies became one of two conventions used to describe point groups (the other being Hermann–Mauguin notation). Also in this time, van der Waerden notation became popular for the usage of two-component spinors (Weyl spinors) in four spacetime dimensions. Arend Heyting would introduce Heyting algebra and Heyting arithmetic. The arrow, e.g., →, was developed for function notation in 1936 by Øystein Ore to denote images of specific elements.See Galois connections.Oystein Ore would also write
Number Theory and Its History
. Later, in 1940, it took its present form, e.g., ''f: X → Y'', through the work of Witold Hurewicz. Werner Heisenberg, in 1941, proposed the S-matrix theory of particle interactions. Bra–ket notation (Dirac notation) is a standard notation for describing quantum states, composed of bracket, angle brackets and vertical bars. It can also be used to denote abstract vector space, vectors and linear functionals. It is so called because the inner product (or
Bra–ket notation (Dirac notation) is a standard notation for describing quantum states, composed of bracket, angle brackets and vertical bars. It can also be used to denote abstract vector space, vectors and linear functionals. It is so called because the inner product (or
 A step towards the Standard Model was Sheldon Glashow's discovery, in 1960, of a way to combine the electromagnetism, electromagnetic and weak interactions. In 1967, Steven Weinberg and Abdus Salam incorporated the Higgs mechanism into Glashow's electroweak theory, giving it its modern form. The Higgs mechanism is believed to give rise to the masses of all the elementary particles in the Standard Model. This includes the masses of the W and Z bosons, and the masses of the fermions – i.e. the quarks and leptons. Also in 1967, Bryce DeWitt published Wheeler–DeWitt equation, his equation under the name "''Wheeler–DeWitt equation, Einstein–Schrödinger equation''" (later renamed the "''John Archibald Wheeler, Wheeler–DeWitt equation''"). In 1969, Yoichiro Nambu, Holger Bech Nielsen, and Leonard Susskind described space and time in String theory, terms of strings. In 1970, Pierre Ramond develop two-dimensional supersymmetries. Michio Kaku and Keiji Kikkawa would afterwards formulate string variations. In 1972, Michael Artin, Alexandre Grothendieck, Jean-Louis Verdier propose the Grothendieck universe.
After the Neutral current, neutral weak currents caused by boson exchange Gargamelle, were discovered at CERN in 1973, the electroweak theory became widely accepted and Glashow, Salam, and Weinberg shared the 1979 Nobel Prize in Physics for discovering it. The theory of the strong interaction, to which many contributed, acquired its modern form around 1973–74. With the establishment of quantum chromodynamics, a finalized a set of fundamental and exchange particles, which allowed for the establishment of a "Standard Model, standard model" based on the mathematics of Gauge theory, gauge invariance, which successfully described all forces except for gravity, and which remains generally accepted within the domain to which it is designed to be applied. In the late 1970s, William Thurston introduced hyperbolic geometry into the Knot theory, study of knots with the geometrization conjecture, hyperbolization theorem. The orbifold notation system, invented by Thurston, has been developed for representing types of symmetry groups in two-dimensional spaces of constant curvature. In 1978, Shing-Tung Yau deduced that the Calabi conjecture have Ricci-flat manifold, Ricci flat metrics. In 1979, Daniel Friedan showed that the equations of motions of string theory are abstractions of Einstein equations of General Relativity.
The first superstring revolution is composed of mathematical equations developed between 1984 and 1986. In 1984, Vaughan Jones deduced the Jones polynomial and subsequent contributions from Edward Witten, Maxim Kontsevich, and others, revealed deep connections between knot theory and mathematical methods in statistical mechanics and quantum field theory. According to string theory, all particles in the "particle zoo" have a common ancestor, namely a String (physics), vibrating string. In 1985, Philip Candelas, Gary Horowitz, Andrew Strominger, and Edward Witten would publish "Vacuum configurations for superstrings" Later, the tetrad formalism (tetrad (index notation), tetrad index notation) would be introduced as an approach to general relativity that replaces the choice of a coordinate basis by the less restrictive choice of a local basis for the tangent bundle.A locally defined set of four linearly independent vector fields called a Tetrad (general relativity), tetrad
In the 1990s, Roger Penrose would propose Penrose graphical notation (tensor diagram notation) as a, usually handwritten, visual depiction of multilinear functions or tensors. Penrose would also introduce abstract index notation.His usage of the Einstein summation was in order to offset the inconvenience in describing tensor contraction, contractions and covariant derivative, covariant differentiation in modern abstract tensor notation, while maintaining explicit covariance of the expressions involved. In 1995, Edward Witten suggested M-theory and subsequently used it to explain some observed Duality (mathematics), dualities, initiating the second superstring revolution.See also: String theory landscape and Swampland (physics), Swampland
A step towards the Standard Model was Sheldon Glashow's discovery, in 1960, of a way to combine the electromagnetism, electromagnetic and weak interactions. In 1967, Steven Weinberg and Abdus Salam incorporated the Higgs mechanism into Glashow's electroweak theory, giving it its modern form. The Higgs mechanism is believed to give rise to the masses of all the elementary particles in the Standard Model. This includes the masses of the W and Z bosons, and the masses of the fermions – i.e. the quarks and leptons. Also in 1967, Bryce DeWitt published Wheeler–DeWitt equation, his equation under the name "''Wheeler–DeWitt equation, Einstein–Schrödinger equation''" (later renamed the "''John Archibald Wheeler, Wheeler–DeWitt equation''"). In 1969, Yoichiro Nambu, Holger Bech Nielsen, and Leonard Susskind described space and time in String theory, terms of strings. In 1970, Pierre Ramond develop two-dimensional supersymmetries. Michio Kaku and Keiji Kikkawa would afterwards formulate string variations. In 1972, Michael Artin, Alexandre Grothendieck, Jean-Louis Verdier propose the Grothendieck universe.
After the Neutral current, neutral weak currents caused by boson exchange Gargamelle, were discovered at CERN in 1973, the electroweak theory became widely accepted and Glashow, Salam, and Weinberg shared the 1979 Nobel Prize in Physics for discovering it. The theory of the strong interaction, to which many contributed, acquired its modern form around 1973–74. With the establishment of quantum chromodynamics, a finalized a set of fundamental and exchange particles, which allowed for the establishment of a "Standard Model, standard model" based on the mathematics of Gauge theory, gauge invariance, which successfully described all forces except for gravity, and which remains generally accepted within the domain to which it is designed to be applied. In the late 1970s, William Thurston introduced hyperbolic geometry into the Knot theory, study of knots with the geometrization conjecture, hyperbolization theorem. The orbifold notation system, invented by Thurston, has been developed for representing types of symmetry groups in two-dimensional spaces of constant curvature. In 1978, Shing-Tung Yau deduced that the Calabi conjecture have Ricci-flat manifold, Ricci flat metrics. In 1979, Daniel Friedan showed that the equations of motions of string theory are abstractions of Einstein equations of General Relativity.
The first superstring revolution is composed of mathematical equations developed between 1984 and 1986. In 1984, Vaughan Jones deduced the Jones polynomial and subsequent contributions from Edward Witten, Maxim Kontsevich, and others, revealed deep connections between knot theory and mathematical methods in statistical mechanics and quantum field theory. According to string theory, all particles in the "particle zoo" have a common ancestor, namely a String (physics), vibrating string. In 1985, Philip Candelas, Gary Horowitz, Andrew Strominger, and Edward Witten would publish "Vacuum configurations for superstrings" Later, the tetrad formalism (tetrad (index notation), tetrad index notation) would be introduced as an approach to general relativity that replaces the choice of a coordinate basis by the less restrictive choice of a local basis for the tangent bundle.A locally defined set of four linearly independent vector fields called a Tetrad (general relativity), tetrad
In the 1990s, Roger Penrose would propose Penrose graphical notation (tensor diagram notation) as a, usually handwritten, visual depiction of multilinear functions or tensors. Penrose would also introduce abstract index notation.His usage of the Einstein summation was in order to offset the inconvenience in describing tensor contraction, contractions and covariant derivative, covariant differentiation in modern abstract tensor notation, while maintaining explicit covariance of the expressions involved. In 1995, Edward Witten suggested M-theory and subsequently used it to explain some observed Duality (mathematics), dualities, initiating the second superstring revolution.See also: String theory landscape and Swampland (physics), Swampland
 John Horton Conway, John Conway would further various notations, including the Conway chained arrow notation, the Conway notation (knot theory), Conway notation of knot theory, and the Conway polyhedron notation. The Coxeter notation system classifies symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter and Norman Johnson (mathematician), Norman Johnson more comprehensively defined it.
Combinatorics, Combinatorial LCF notationDevised by Joshua Lederberg and extended by Harold Scott MacDonald Coxeter, Coxeter and Robert Frucht, Frucht has been developed for the representation of cubic graphs that are Hamiltonian path, Hamiltonian. The cycle notation is the convention for writing down a permutation in terms of its constituent cyclic permutation, cycles. This is also called circular notation and the permutation called a ''cyclic'' or ''circular'' permutation.
John Horton Conway, John Conway would further various notations, including the Conway chained arrow notation, the Conway notation (knot theory), Conway notation of knot theory, and the Conway polyhedron notation. The Coxeter notation system classifies symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter and Norman Johnson (mathematician), Norman Johnson more comprehensively defined it.
Combinatorics, Combinatorial LCF notationDevised by Joshua Lederberg and extended by Harold Scott MacDonald Coxeter, Coxeter and Robert Frucht, Frucht has been developed for the representation of cubic graphs that are Hamiltonian path, Hamiltonian. The cycle notation is the convention for writing down a permutation in terms of its constituent cyclic permutation, cycles. This is also called circular notation and the permutation called a ''cyclic'' or ''circular'' permutation.
On Computable Numbers, With an Application to the Entscheidungsproblem
.And, in 1938, . John von Neumann, pioneer of the digital computer and of computer science,Among von Neumann's other contributions include the application of operator theory to quantum mechanics, in the development of functional analysis, and on various forms of operator theory. in 1945, writes the unfinished work, incomplete ''First Draft of a Report on the EDVAC''. In 1962, Kenneth E. Iverson developed an integral part notation, which became APL (programming language), APL, for manipulating arrays that he taught to his students, and described in his book ''A Programming Language''. In 1970, Edgar F. Codd proposed relational algebra as a relational model, relational model of data for database query languages. In 1971, Stephen Cook publishes "P versus NP problem, The complexity of theorem proving procedures" In the 1970s within computer architecture, Quote notation was developed for a representing number system of
 In the history of mathematical notation, ideographic symbol notation has come full circle with the rise of computer visualization systems. The notations can be applied to abstract visualizations, such as for rendering some projections of a Calabi–Yau manifold, Calabi–Yau manifold. Examples of abstract visualization which properly belong to the mathematical imagination can be found in computer graphics. The need for such models abounds, for example, when the measures for the subject of study are actually random variables and not really ordinary mathematical functions.
In the history of mathematical notation, ideographic symbol notation has come full circle with the rise of computer visualization systems. The notations can be applied to abstract visualizations, such as for rendering some projections of a Calabi–Yau manifold, Calabi–Yau manifold. Examples of abstract visualization which properly belong to the mathematical imagination can be found in computer graphics. The need for such models abounds, for example, when the measures for the subject of study are actually random variables and not really ordinary mathematical functions.
A Short Account of the History of Mathematics
By Walter William Rouse Ball.
A Primer of the History of Mathematics
By Walter William Rouse Ball.
A History of Elementary Mathematics
With Hints on Methods of Teaching. By Florian Cajori.
A History of Elementary Mathematics
By Florian Cajori.
A History of Mathematics
By Florian Cajori.
A Short History of Greek Mathematics
By James Gow (Author), James Gow.
On the Development of Mathematical Thought During the Nineteenth Century
By John Theodore Merz.
A New Mathematical and Philosophical Dictionary
By Peter Barlow.
Historical Introduction to Mathematical Literature
By George Abram Miller
A Brief History of Mathematics
By Karl Fink, Wooster Woodruff Beman, David Eugene Smith
History of Modern Mathematics
By David Eugene Smith.
History of modern mathematics
By David Eugene Smith, Mansfield Merriman. ;Other * Principia Mathematica
Volume 1
Volume 2
By Alfred North Whitehead, Bertrand Russell.
The Mathematical Principles of Natural Philosophy
Volume 1, Issue 1. By Sir Isaac Newton, Andrew Motte, William Davis, John Machin, William Emerson.
General investigations of curved surfaces of 1827 and 1825
By Carl Friedrich Gaus.
Mathematical Notation: Past and Future
files.chem.vt.edu.
Some Common Mathematical Symbols and Abbreviations (with History)
Isaiah Lankham, Bruno Nachtergaele, Anne Schilling. {{History of science History of mathematics, Mathematical notation Mathematical notation Articles which contain graphical timelines
cultural diffusion
In cultural anthropology and cultural geography, cultural diffusion, as conceptualized by Leo Frobenius in his 1897/98 publication ''Der westafrikanische Kulturkreis'', is the spread of cultural items—such as ideas, styles, religions, technologi ...
of mathematical symbol
A mathematical symbol is a figure or a combination of figures that is used to represent a mathematical object, an action on mathematical objects, a relation between mathematical objects, or for structuring the other symbols that occur in a formula ...
s and the conflict of the methods of notation confronted in a notation's move to popularity or inconspicuousness. Mathematical notation
Mathematical notation consists of using symbols for representing operations, unspecified numbers, relations and any other mathematical objects, and assembling them into expressions and formulas. Mathematical notation is widely used in mathematic ...
comprises the symbol
A symbol is a mark, sign, or word that indicates, signifies, or is understood as representing an idea, object, or relationship. Symbols allow people to go beyond what is known or seen by creating linkages between otherwise very different conc ...
s used to write mathematical equation
In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign . The word ''equation'' and its cognates in other languages may have subtly different meanings; for example, in ...
s and formula
In science, a formula is a concise way of expressing information symbolically, as in a mathematical formula or a ''chemical formula''. The informal use of the term ''formula'' in science refers to the general construct of a relationship betwee ...
s. Notation generally implies a set of well-defined
In mathematics, a well-defined expression or unambiguous expression is an expression whose definition assigns it a unique interpretation or value. Otherwise, the expression is said to be ''not well defined'', ill defined or ''ambiguous''. A funct ...
representations of quantities and symbols operators. The history includes Hindu–Arabic numerals, letters from the Roman
Roman or Romans most often refers to:
*Rome, the capital city of Italy
*Ancient Rome, Roman civilization from 8th century BC to 5th century AD
*Roman people, the people of ancient Rome
*''Epistle to the Romans'', shortened to ''Romans'', a letter ...
, Greek
Greek may refer to:
Greece
Anything of, from, or related to Greece, a country in Southern Europe:
*Greeks, an ethnic group.
*Greek language, a branch of the Indo-European language family.
**Proto-Greek language, the assumed last common ancestor ...
, Hebrew
Hebrew (; ; ) is a Northwest Semitic language of the Afroasiatic language family. Historically, it is one of the spoken languages of the Israelites and their longest-surviving descendants, the Jews and Samaritans. It was largely preserved ...
, and German
German(s) may refer to:
* Germany (of or related to)
**Germania (historical use)
* Germans, citizens of Germany, people of German ancestry, or native speakers of the German language
** For citizens of Germany, see also German nationality law
**Ger ...
alphabet
An alphabet is a standardized set of basic written graphemes (called letters) that represent the phonemes of certain spoken languages. Not all writing systems represent language in this way; in a syllabary, each character represents a syll ...
s, and a host of symbols invented by mathematicians over the past several centuries.
The development of mathematical notation can be divided in stages. The "''rhetorical
Rhetoric () is the art of persuasion, which along with grammar and logic (or dialectic), is one of the three ancient arts of discourse. Rhetoric aims to study the techniques writers or speakers utilize to inform, persuade, or motivate parti ...
''" stage is where calculations are performed by words and no symbols are used. The "''syncopated
In music, syncopation is a variety of rhythms played together to make a piece of music, making part or all of a tune or piece of music off-beat. More simply, syncopation is "a disturbance or interruption of the regular flow of rhythm": a "place ...
''" stage is where frequently used operations and quantities are represented by symbolic syntactical
In linguistics, syntax () is the study of how words and morphemes combine to form larger units such as phrases and sentences. Central concerns of syntax include word order, grammatical relations, hierarchical sentence structure (constituency), ...
abbreviations. From ancient times through the post-classical age,Or the Middle Ages. bursts of mathematical creativity were often followed by centuries of stagnation. As the early modern age opened and the worldwide spread of knowledge began, written examples of mathematical developments came to light. The "''symbolic''" stage is where comprehensive systems of notation supersede rhetoric. Beginning in Italy in the 16th century, new mathematical developments, interacting with new scientific discoveries, were made at an increasing pace that continues through the present day. This symbolic system was in use by medieval Indian mathematicians and in Europe since the middle of the 17th century, and has continued to develop in the contemporary era
Contemporary history, in English-language historiography, is a subset of modern history that describes the historical period from approximately 1945 to the present. Contemporary history is either a subset of the late modern period, or it i ...
.
The area of study known as the history of mathematics
The history of mathematics deals with the origin of discoveries in mathematics and the mathematical methods and notation of the past. Before the modern age and the worldwide spread of knowledge, written examples of new mathematical developments ...
is primarily an investigation into the origin of discoveries in mathematics and, the focus here, the investigation into the mathematical methods and notation of the past.
Rhetorical stage
Although the history commences with that of the Ionian schools, there is no doubt that thoseAncient Greek
Ancient Greek includes the forms of the Greek language used in ancient Greece and the ancient world from around 1500 BC to 300 BC. It is often roughly divided into the following periods: Mycenaean Greek (), Dark Ages (), the Archaic peri ...
s who paid attention to it were largely indebted to the previous investigations of the Ancient Egyptians and Ancient Phoenicians. Numerical notation's distinctive feature, i.e. symbols having local as well as intrinsic values (arithmetic
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers— addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th ...
), implies a state of civilization
A civilization (or civilisation) is any complex society characterized by the development of a state, social stratification, urbanization, and symbolic systems of communication beyond natural spoken language (namely, a writing system).
Ci ...
at the period of its invention. Our knowledge of the mathematical attainments of these early peoples, to which this section is devoted, is imperfect and the following brief notes be regarded as a summary of the conclusions which seem most probable, and the history of mathematics begins with the symbolic sections.
Many areas of mathematics began with the study of real world problems, before the underlying rules and concepts were identified and defined as abstract structure
An abstract structure is an abstraction that might be of the Euclidean space, geometric spaces or a set structure, or a hypostatic abstraction that is defined by a set of mathematical theorems and laws, properties and relationships in a way that is ...
s. For example, geometry has its origins in the calculation of distances and area
Area is the quantity that expresses the extent of a region on the plane or on a curved surface. The area of a plane region or ''plane area'' refers to the area of a shape
A shape or figure is a graphics, graphical representation of an obje ...
s in the real world; algebra started with methods of solving problems in arithmetic
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers— addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th ...
.
There can be no doubt that most early peoples which have left records knew something of numeration
A numeral system (or system of numeration) is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using digits or other symbols in a consistent manner.
The same sequence of symbo ...
and mechanics
Mechanics (from Ancient Greek: μηχανική, ''mēkhanikḗ'', "of machines") is the area of mathematics and physics concerned with the relationships between force, matter, and motion among physical objects. Forces applied to objects r ...
, and that a few were also acquainted with the elements of land-surveying. In particular, the Egyptians paid attention to geometry and numbers, and the Phoenicians to practical arithmetic, book-keeping, navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navigation, ...
, and land-surveying. The results attained by these people seem to have been accessible, under certain conditions, to travelers. It is probable that the knowledge of the Egyptians and Phoenicians was largely the result of observation
Observation is the active acquisition of information from a primary source. In living beings, observation employs the senses. In science, observation can also involve the perception and recording of data via the use of scientific instruments. The ...
and measurement
Measurement is the quantification of attributes of an object or event, which can be used to compare with other objects or events.
In other words, measurement is a process of determining how large or small a physical quantity is as compared ...
, and represented the accumulated experience of many ages.
Beginning of notation
 Written mathematics began with numbers expressed as
Written mathematics began with numbers expressed as tally marks
Tally marks, also called hash marks, are a unary numeral system ( arguably).
They are a form of numeral used for counting. They are most useful in counting or tallying ongoing results, such as the score in a game or sport, as no intermediate ...
, with each tally representing a single unit. The numerical symbols consisted probably of strokes or notches cut in wood or stone, and intelligible alike to all nations.Such characters, in fact, are preserved with little alteration in the Roman notation
Roman numerals are a numeral system that originated in ancient Rome and remained the usual way of writing numbers throughout Europe well into the Late Middle Ages. Numbers are written with combinations of letters from the Latin alphabet, eac ...
, an account of which may be found in John Leslie's Philosophy of Arithmetic. For example, one notch in a bone represented one animal, or person, or anything else. The peoples with whom the Greeks of Asia Minor (amongst whom notation in western history begins) were likely to have come into frequent contact were those inhabiting the eastern littoral
The littoral zone or nearshore is the part of a sea, lake, or river that is close to the shore. In coastal ecology, the littoral zone includes the intertidal zone extending from the high water mark (which is rarely inundated), to coastal areas ...
of the Mediterranean: and Greek tradition uniformly assigned the special development of geometry to the Egyptians, and that of the science of numbersNumber theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777� ...
is the branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
s as well as the properties of objects made out of integers (e.g., rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all ration ...
s) or defined as generalizations of the integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language ...
s (e.g., algebraic integer
In algebraic number theory, an algebraic integer is a complex number which is integral over the integers. That is, an algebraic integer is a complex root of some monic polynomial (a polynomial whose leading coefficient is 1) whose coefficients ...
s). either to the Egyptians or to the Phoenicians.
The Ancient Egyptians had a symbolic notation which was the numeration by Hieroglyphics. The Egyptian mathematics
Ancient Egyptian mathematics is the mathematics that was developed and used in Ancient Egypt 3000 to c. , from the Old Kingdom of Egypt until roughly the beginning of Hellenistic Egypt. The ancient Egyptians utilized a numeral system for count ...
had a symbol for one, ten, one hundred, one thousand, ten thousand, one hundred thousand, and one million. Smaller digits were placed on the left of the number, as they are in Hindu–Arabic numerals. Later, the Egyptians used hieratic
Hieratic (; grc, ἱερατικά, hieratiká, priestly) is the name given to a cursive writing system used for Ancient Egyptian and the principal script used to write that language from its development in the third millennium BC until the ris ...
instead of hieroglyphic
Egyptian hieroglyphs (, ) were the formal writing system used in Ancient Egypt, used for writing the Egyptian language. Hieroglyphs combined logographic, syllabic and alphabetic elements, with some 1,000 distinct characters.There were about 1,00 ...
script to show numbers. Hieratic was more like cursive and replaced several groups of symbols with individual ones. For example, the four vertical lines used to represent four were replaced by a single horizontal line. This is found in the Rhind Mathematical Papyrus
The Rhind Mathematical Papyrus (RMP; also designated as papyrus British Museum 10057 and pBM 10058) is one of the best known examples of ancient Egyptian mathematics. It is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased ...
(c. 2000–1800 BC) and the Moscow Mathematical Papyrus
The Moscow Mathematical Papyrus, also named the Golenishchev Mathematical Papyrus after its first non-Egyptian owner, Egyptologist Vladimir Golenishchev, is an ancient Egyptian mathematical papyrus containing several problems in arithmetic, geom ...
(c. 1890 BC). The system the Egyptians used was discovered and modified by many other civilizations in the Mediterranean. The Egyptians also had symbols for basic operations: legs going forward represented addition, and legs walking backward to represent subtraction.
The Mesopotamians
Mesopotamia ''Mesopotamíā''; ar, بِلَاد ٱلرَّافِدَيْن or ; syc, ܐܪܡ ܢܗܪ̈ܝܢ, or , ) is a historical region of Western Asia situated within the Tigris–Euphrates river system, in the northern part of the F ...
had symbols for each power of ten. Later, they wrote their numbers in almost exactly the same way done in modern times. Instead of having symbols for each power of ten, they would just put the coefficient
In mathematics, a coefficient is a multiplicative factor in some term of a polynomial, a series, or an expression; it is usually a number, but may be any expression (including variables such as , and ). When the coefficients are themselves var ...
of that number. Each digit was separated by only a space, but by the time of Alexander the Great
Alexander III of Macedon ( grc, wikt:Ἀλέξανδρος, Ἀλέξανδρος, Alexandros; 20/21 July 356 BC – 10/11 June 323 BC), commonly known as Alexander the Great, was a king of the Ancient Greece, ancient Greek kingdom of Maced ...
, they had created a symbol that represented zero and was a placeholder. The Mesopotamians also used a sexagesimal
Sexagesimal, also known as base 60 or sexagenary, is a numeral system with sixty as its base. It originated with the ancient Sumerians in the 3rd millennium BC, was passed down to the ancient Babylonians, and is still used—in a modified form� ...
system, that is base sixty. It is this system that is used in modern times when measuring time and angles. Babylonian mathematics is derived from more than 400 clay tablets unearthed since the 1850s. Written in Cuneiform script
Cuneiform is a logo-syllabic script that was used to write several languages of the Ancient Middle East. The script was in active use from the early Bronze Age until the beginning of the Common Era. It is named for the characteristic wedge-sha ...
, tablets were inscribed whilst the clay was moist, and baked hard in an oven or by the heat of the sun. Some of these appear to be graded homework. The earliest evidence of written mathematics dates back to the ancient Sumer
Sumer () is the earliest known civilization in the historical region of southern Mesopotamia (south-central Iraq), emerging during the Chalcolithic and early Bronze Ages between the sixth and fifth millennium BC. It is one of the cradles of c ...
ians and the system of metrology
Metrology is the scientific study of measurement. It establishes a common understanding of units, crucial in linking human activities. Modern metrology has its roots in the French Revolution's political motivation to standardise units in Fran ...
from 3000 BC. From around 2500 BC onwards, the Sumerians wrote multiplication table
In mathematics, a multiplication table (sometimes, less formally, a times table) is a mathematical table used to define a multiplication operation for an algebraic system.
The decimal multiplication table was traditionally taught as an essenti ...
s on clay tablets and dealt with geometrical
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is ca ...
exercises and division
Division or divider may refer to:
Mathematics
*Division (mathematics), the inverse of multiplication
*Division algorithm, a method for computing the result of mathematical division
Military
*Division (military), a formation typically consisting ...
problems. The earliest traces of the Babylonian numerals also date back to this period.
The majority of Mesopotamian clay tablets date from 1800 to 1600 BC, and cover topics which include fractions, algebra, quadratic and cubic equations, and the calculation of regular, reciprocal
Reciprocal may refer to:
In mathematics
* Multiplicative inverse, in mathematics, the number 1/''x'', which multiplied by ''x'' gives the product 1, also known as a ''reciprocal''
* Reciprocal polynomial, a polynomial obtained from another pol ...
and pairs
Concentration, also known as Memory, Shinkei-suijaku (Japanese meaning "nervous breakdown"), Matching Pairs, Match Match, Match Up, Pelmanism, Pexeso or simply Pairs, is a card game in which all of the cards are laid face down on a surface and tw ...
. The tablets also include multiplication tables and methods for solving linear
Linearity is the property of a mathematical relationship (''function'') that can be graphically represented as a straight line. Linearity is closely related to '' proportionality''. Examples in physics include rectilinear motion, the linear r ...
and quadratic equation
In algebra, a quadratic equation () is any equation that can be rearranged in standard form as
ax^2 + bx + c = 0\,,
where represents an unknown (mathematics), unknown value, and , , and represent known numbers, where . (If and then the equati ...
s. The Babylonian tablet YBC 7289
YBC 7289 is a Babylonian clay tablet notable for containing an accurate sexagesimal approximation to the square root of 2, the length of the diagonal of a unit square. This number is given to the equivalent of six decimal digits, "the greatest ...
gives an approximation of accurate to five decimal places. Babylonian mathematics were written using a sexagesimal
Sexagesimal, also known as base 60 or sexagenary, is a numeral system with sixty as its base. It originated with the ancient Sumerians in the 3rd millennium BC, was passed down to the ancient Babylonians, and is still used—in a modified form� ...
(base-60) numeral system
A numeral system (or system of numeration) is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using Numerical digit, digits or other symbols in a consistent manner.
The same s ...
. From this derives the modern-day usage of 60 seconds in a minute, 60 minutes in an hour, and 360 (60 × 6) degrees in a circle, as well as the use of minutes and seconds of arc
A minute of arc, arcminute (arcmin), arc minute, or minute arc, denoted by the symbol , is a unit of angular measurement equal to of one degree. Since one degree is of a turn (or complete rotation), one minute of arc is of a turn. The ...
to denote fractions of a degree. Babylonian advances in mathematics were facilitated by the fact that 60 has many divisors: the reciprocal of any integer which is a multiple of divisors of 60 has a finite expansion in base 60. (In decimal arithmetic, only reciprocals of multiples of 2 and 5 have finite decimal expansions.) Also, unlike the Egyptians, Greeks, and Romans, the Babylonians had a true place-value system, where digits written in the left column represented larger values, much as in the decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers of the Hindu–Arabic numeral ...
system. They lacked, however, an equivalent of the decimal point, and so the place value of a symbol often had to be inferred from the context.
Syncopated stage
 The history of mathematics cannot with certainty be traced back to any school or period before that of the Ionian Greeks, but the subsequent history may be divided into periods, the distinctions between which are tolerably well marked. Greek mathematics, which originated with the study of geometry, tended from its commencement to be deductive and scientific. Since the fourth century AD,
The history of mathematics cannot with certainty be traced back to any school or period before that of the Ionian Greeks, but the subsequent history may be divided into periods, the distinctions between which are tolerably well marked. Greek mathematics, which originated with the study of geometry, tended from its commencement to be deductive and scientific. Since the fourth century AD, Pythagoras
Pythagoras of Samos ( grc, Πυθαγόρας ὁ Σάμιος, Pythagóras ho Sámios, Pythagoras the Samos, Samian, or simply ; in Ionian Greek; ) was an ancient Ionians, Ionian Ancient Greek philosophy, Greek philosopher and the eponymou ...
has commonly been given credit for discovering the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
, a theorem in geometry that states that in a right-angled triangle the area of the square on the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares of the other two sides.That is, . The ancient mathematical texts are available with the prior mentioned Ancient Egyptians notation and with Plimpton 322
Plimpton 322 is a Babylonian clay tablet, notable as containing an example of Babylonian mathematics. It has number 322 in the G.A. Plimpton Collection at Columbia University. This tablet, believed to have been written about 1800 BC, has a table ...
(Babylonian mathematics c. 1900 BC). The study of mathematics as a subject in its own right begins in the 6th century BC with the Pythagoreans
Pythagoreanism originated in the 6th century BC, based on and around the teachings and beliefs held by Pythagoras and his followers, the Pythagoreans. Pythagoras established the first Pythagorean community in the ancient Greek colony of Kroton, ...
, who coined the term "mathematics" from the ancient Greek ''μάθημα'' (''mathema''), meaning "subject of instruction".
Plato
Plato ( ; grc-gre, Πλάτων ; 428/427 or 424/423 – 348/347 BC) was a Greek philosopher born in Athens during the Classical period in Ancient Greece. He founded the Platonist school of thought and the Academy, the first institution ...
's influence has been especially strong in mathematics and the sciences. He helped to distinguish between pure
Pure may refer to:
Computing
* A pure function
* A pure virtual function
* PureSystems, a family of computer systems introduced by IBM in 2012
* Pure Software, a company founded in 1991 by Reed Hastings to support the Purify tool
* Pure-FTPd, F ...
and applied mathematics
Applied mathematics is the application of mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and industry. Thus, applied mathematics is a combination of mathematical s ...
by widening the gap between "arithmetic", now called number theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777� ...
and "logistic", now called arithmetic
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers— addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th ...
. Greek mathematics
Greek mathematics refers to mathematics texts and ideas stemming from the Archaic through the Hellenistic and Roman periods, mostly extant from the 7th century BC to the 4th century AD, around the shores of the Eastern Mediterranean. Greek mathem ...
greatly refined the methods (especially through the introduction of deductive reasoning and mathematical rigor
Rigour (British English) or rigor (American English; see spelling differences) describes a condition of stiffness or strictness. These constraints may be environmentally imposed, such as "the rigours of famine"; logically imposed, such as m ...
in proofs
Proof most often refers to:
* Proof (truth), argument or sufficient evidence for the truth of a proposition
* Alcohol proof, a measure of an alcoholic drink's strength
Proof may also refer to:
Mathematics and formal logic
* Formal proof, a co ...
) and expanded the subject matter of mathematics. Aristotle
Aristotle (; grc-gre, Ἀριστοτέλης ''Aristotélēs'', ; 384–322 BC) was a Greek philosopher and polymath during the Classical period in Ancient Greece. Taught by Plato, he was the founder of the Peripatetic school of phil ...
is credited with what later would be called the law of excluded middle
In logic, the law of excluded middle (or the principle of excluded middle) states that for every proposition, either this proposition or its negation is true. It is one of the so-called three laws of thought, along with the law of noncontradic ...
.
''Abstract Mathematics'' is what treats of magnitudeMagnitude (mathematics)
In mathematics, the magnitude or size of a mathematical object is a property which determines whether the object is larger or smaller than other objects of the same kind. More formally, an object's magnitude is the displayed result of an order th ...
, the relative size of an object; Magnitude (vector)
In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the origin: it commutes with scaling, obeys a form of the triangle inequality, and is ze ...
, a term for the size or length of a vector; Scalar (mathematics)
A scalar is an element of a field which is used to define a ''vector space''.
In linear algebra, real numbers or generally elements of a field are called scalars and relate to vectors in an associated vector space through the operation of scala ...
, a quantity defined only by its magnitude; Euclidean vector
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Vectors can be added to other vectors ac ...
, a quantity defined by both its magnitude and its direction; Order of magnitude
An order of magnitude is an approximation of the logarithm of a value relative to some contextually understood reference value, usually 10, interpreted as the base of the logarithm and the representative of values of magnitude one. Logarithmic dis ...
, the class of scale having a fixed value ratio to the preceding class. or quantity
Quantity or amount is a property that can exist as a Counting, multitude or Magnitude (mathematics), magnitude, which illustrate discontinuity (mathematics), discontinuity and continuum (theory), continuity. Quantities can be compared in terms o ...
, absolutely and generally conferred, without regard to any species of particular magnitude, such as arithmetic
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers— addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th ...
and geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, In this sense, abstract mathematics is opposed to mixed mathematics, wherein simple and abstract properties, and the relations of quantities primitively considered in mathematics, are applied to sensible objects, and by that means become intermixed with physical considerations, such as in hydrostatics
Fluid statics or hydrostatics is the branch of fluid mechanics that studies the condition of the equilibrium of a floating body and submerged body " fluids at hydrostatic equilibrium and the pressure in a fluid, or exerted by a fluid, on an imm ...
, optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultraviole ...
, and navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navigation, ...
.The new encyclopædia; or, Universal dictionary of arts and sciences. By Encyclopaedia Perthensi. Pg 49
Archimedes
Archimedes of Syracuse (;; ) was a Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is regarded as one of the leading scientists ...
is generally considered to be the greatest mathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems.
Mathematicians are concerned with numbers, data, quantity, structure, space, models, and change.
History
On ...
of antiquity and one of the greatest of all time. He used the method of exhaustion
The method of exhaustion (; ) is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area bet ...
to calculate the area
Area is the quantity that expresses the extent of a region on the plane or on a curved surface. The area of a plane region or ''plane area'' refers to the area of a shape
A shape or figure is a graphics, graphical representation of an obje ...
under the arc of a parabola
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
One descript ...
with the summation of an infinite series, and gave a remarkably accurate approximation of pi. He also defined the spiral
In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point.
Helices
Two major definitions of "spiral" in the American Heritage Dictionary are:volume
Volume is a measure of occupied three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). The de ...
s of surfaces of revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve (the generatrix) around an axis of rotation.
Examples of surfaces of revolution generated by a straight line are cylindrical and conical surfaces depending on wh ...
and an ingenious system for expressing very large numbers.
 In the historical development of geometry, the steps in the abstraction of geometry were made by the ancient Greeks.
In the historical development of geometry, the steps in the abstraction of geometry were made by the ancient Greeks. Euclid's Elements
The ''Elements'' ( grc, Στοιχεῖα ''Stoikheîa'') is a mathematical treatise consisting of 13 books attributed to the ancient Greek mathematician Euclid in Alexandria, Ptolemaic Egypt 300 BC. It is a collection of definitions, postulat ...
being the earliest extant documentation of the axioms of plane geometry— though Proclus tells of an earlier axiomatisation
In mathematics and logic, an axiomatic system is any set of axioms from which some or all axioms can be used in conjunction to logically derive theorems. A theory is a consistent, relatively-self-contained body of knowledge which usually conta ...
by Hippocrates of Chios
Hippocrates of Chios ( grc-gre, Ἱπποκράτης ὁ Χῖος; c. 470 – c. 410 BC) was an ancient Greek mathematician, geometer, and astronomer.
He was born on the isle of Chios, where he was originally a merchant. After some misadve ...
. Euclid's ''Elements'' (c. 300 BC) is one of the oldest extant Greek mathematical treatisesAutolycus
In Greek mythology, Autolycus (; Ancient Greek: Αὐτόλυκος ''Autolykos'' 'the wolf itself') was a successful robber who had even the power of metamorphosing both the stolen goods and himself. He had his residence on Mount Parnassus and w ...
' On the Moving Sphere is another ancient mathematical manuscript of the time. and consisted of 13 books written in Alexandria; collecting theorems proven by other mathematicians, supplemented by some original work.Proclus
Proclus Lycius (; 8 February 412 – 17 April 485), called Proclus the Successor ( grc-gre, Πρόκλος ὁ Διάδοχος, ''Próklos ho Diádokhos''), was a Greek Neoplatonist philosopher, one of the last major classical philosophers ...
, a Greek mathematician who lived several centuries after Euclid, wrote in his commentary of the Elements: "Euclid, who put together the Elements, collecting many of Eudoxus' theorems, perfecting many of Theaetetus', and also bringing to irrefragable demonstration the things which were only somewhat loosely proved by his predecessors". The document is a successful collection of definitions, postulates (axioms), propositions (theorems and constructions), and mathematical proofs of the propositions. Euclid's first theorem is a lemma
Lemma may refer to:
Language and linguistics
* Lemma (morphology), the canonical, dictionary or citation form of a word
* Lemma (psycholinguistics), a mental abstraction of a word about to be uttered
Science and mathematics
* Lemma (botany), a ...
that possesses properties of prime number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
s. The influential thirteen books cover Euclidean geometry, geometric algebra, and the ancient Greek version of algebraic systems and elementary number theory. It was ubiquitous in the Quadrivium
From the time of Plato through the Middle Ages, the ''quadrivium'' (plural: quadrivia) was a grouping of four subjects or arts—arithmetic, geometry, music, and astronomy—that formed a second curricular stage following preparatory work in the ...
and is instrumental in the development of logic, mathematics, and science.
Diophantus of Alexandria
Diophantus of Alexandria ( grc, Διόφαντος ὁ Ἀλεξανδρεύς; born probably sometime between AD 200 and 214; died around the age of 84, probably sometime between AD 284 and 298) was an Alexandrian mathematician, who was the aut ...
was author of a series of books called ''Arithmetica
''Arithmetica'' ( grc-gre, Ἀριθμητικά) is an Ancient Greek text on mathematics written by the mathematician Diophantus () in the 3rd century AD. It is a collection of 130 algebraic problems giving numerical solutions of determinate e ...
'', many of which are now lost. These texts deal with solving algebraic equation
In mathematics, an algebraic equation or polynomial equation is an equation of the form
:P = 0
where ''P'' is a polynomial with coefficients in some field, often the field of the rational numbers. For many authors, the term ''algebraic equation'' ...
s. Boethius
Anicius Manlius Severinus Boethius, commonly known as Boethius (; Latin: ''Boetius''; 480 – 524 AD), was a Roman senator, consul, ''magister officiorum'', historian, and philosopher of the Early Middle Ages. He was a central figure in the tr ...
provided a place for mathematics in the curriculum in the 6th century when he coined the term ''quadrivium'' to describe the study of arithmetic, geometry, astronomy, and music. He wrote ''De institutione arithmetica'', a free translation from the Greek of Nicomachus
Nicomachus of Gerasa ( grc-gre, Νικόμαχος; c. 60 – c. 120 AD) was an important ancient mathematician and music theorist, best known for his works ''Introduction to Arithmetic'' and ''Manual of Harmonics'' in Greek. He was born in ...
's ''Introduction to Arithmetic''; ''De institutione musica'', also derived from Greek sources; and a series of excerpts from Euclid's ''Elements''. His works were theoretical, rather than practical, and were the basis of mathematical study until the recovery of Greek and Arabic mathematical works.
Acrophonic and Milesian numeration
TheGreeks
The Greeks or Hellenes (; el, Έλληνες, ''Éllines'' ) are an ethnic group and nation indigenous to the Eastern Mediterranean and the Black Sea regions, namely Greece, Cyprus, Albania, Italy, Turkey, Egypt, and, to a lesser extent, oth ...
employed Attic numeration
The Attic numerals are a symbolic number notation used by the ancient Greeks. They were also known as Herodianic numerals because they were first described in a 2nd-century manuscript by Herodian; or as acrophonic numerals (from acrophony) ...
, which was based on the system of the Egyptians and was later adapted and used by the Romans
Roman or Romans most often refers to:
*Rome, the capital city of Italy
* Ancient Rome, Roman civilization from 8th century BC to 5th century AD
*Roman people, the people of ancient Rome
*''Epistle to the Romans'', shortened to ''Romans'', a lette ...
. Greek numerals
Greek numerals, also known as Ionic, Ionian, Milesian, or Alexandrian numerals, are a system of writing numbers using the letters of the Greek alphabet. In modern Greece, they are still used for ordinal numbers and in contexts similar to tho ...
one through four were vertical lines, as in the hieroglyphics. The symbol for five was the Greek letter Π (pi), which is the letter of the Greek word for five, ''pente''. Numbers six through nine were ''pente'' with vertical lines next to it. Ten was represented by the letter (Δ) of the word for ten, ''deka'', one hundred by the letter from the word for hundred, etc.
The Ionian numeration
Greek numerals, also known as Ionic, Ionian, Milesian, or Alexandrian numerals, are a system of writing numbers using the letters of the Greek alphabet. In modern Greece, they are still used for ordinal numbers and in contexts similar to those ...
used their entire alphabet including three archaic letters. The numeral notation of the Greeks, though far less convenient than that now in use, was formed on a perfectly regular and scientific plan,A dictionary of science, literature and art, ed. by W.T. Brande. P683
/ref> and could be used with tolerable effect as an instrument of calculation, to which purpose the Roman system was totally inapplicable. The Greeks divided the twenty-four letters of their alphabet into three classes, and, by adding another symbol to each class, they had characters to represent the units, tens, and hundreds. (
Jean Baptiste Joseph Delambre
Jean Baptiste Joseph, chevalier Delambre (19 September 1749 – 19 August 1822) was a French mathematician, astronomer, historian of astronomy, and geodesist. He was also director of the Paris Observatory, and author of well-known books on t ...
's Astronomie Ancienne, t. ii.)
This system appeared in the third century BC, before the letters digamma (Ϝ), koppa (Ϟ), and sampi (Ϡ) became obsolete. When lowercase letters became differentiated from upper case letters, the lower case letters were used as the symbols for notation. Multiples of one thousand were written as the nine numbers with a stroke in front of them: thus one thousand was ",α", two-thousand was ",β", etc. M (for μὐριοι, as in "myriad") was used to multiply numbers by ten thousand. For example, the number 88,888,888 would be written as M,ηωπη*ηωπηBoyer, Carl B. ''A History of Mathematics'', 2nd edition, John Wiley & Sons, Inc., 1991.
Greek mathematical reasoning was almost entirely geometric
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is ca ...
(albeit often used to reason about non-geometric subjects such as number theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777� ...
), and hence the Greeks had no interest in algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics.
Elementary a ...
ic symbols. The great exception was Diophantus
Diophantus of Alexandria ( grc, Διόφαντος ὁ Ἀλεξανδρεύς; born probably sometime between AD 200 and 214; died around the age of 84, probably sometime between AD 284 and 298) was an Alexandrian mathematician, who was the aut ...
of Alexandria
Alexandria ( or ; ar, ٱلْإِسْكَنْدَرِيَّةُ ; grc-gre, Αλεξάνδρεια, Alexándria) is the second largest city in Egypt, and the largest city on the Mediterranean coast. Founded in by Alexander the Great, Alexandria ...
, the great algebraist. His ''Arithmetica
''Arithmetica'' ( grc-gre, Ἀριθμητικά) is an Ancient Greek text on mathematics written by the mathematician Diophantus () in the 3rd century AD. It is a collection of 130 algebraic problems giving numerical solutions of determinate e ...
'' was one of the texts to use symbols in equations. It was not completely symbolic, but was much more so than previous books. An unknown number was called s. The square of s was ; the cube was ; the fourth power was ; and the fifth power was .The expression:would be written as:
SS2 C3 x5 M S4 u6
.
Chinese mathematical notation
Roman numeral
Roman numerals are a numeral system that originated in ancient Rome and remained the usual way of writing numbers throughout Europe well into the Late Middle Ages. Numbers are written with combinations of letters from the Latin alphabet, eac ...
for ten. Nowadays, the huāmǎ system is only used for displaying prices in Chinese markets or on traditional handwritten invoices.
In the history of the Chinese, there were those who were familiar with the sciences of arithmetic, geometry, mechanics, optics, navigation, and astronomy. Mathematics in China
Mathematics in China emerged independently by the 11th century BCE. The Chinese independently developed a real number system that includes significantly large and negative numbers, more than one numeral system ( base 2 and base 10), algebra, geome ...
emerged independently by the 11th century BC. It is almost certain that the Chinese were acquainted with several geometrical or rather architectural implements;such as the rule
Rule or ruling may refer to:
Education
* Royal University of Law and Economics (RULE), a university in Cambodia
Human activity
* The exercise of political or personal control by someone with authority or power
* Business rule, a rule perta ...
, square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adj ...
, compasses
A compass, more accurately known as a pair of compasses, is a technical drawing instrument that can be used for inscribing circles or arcs. As dividers, it can also be used as a tool to mark out distances, in particular, on maps. Compasses c ...
, water level
Water level, also known as gauge height or stage, is the elevation of the free surface of a sea, stream, lake or reservoir relative to a specified vertical datum.ISO 772: 1996. Hydrometric determinations – Vocabulary and symbols.
See also
* ...
(reed level
A reed level is an Arabic invention for determining level for the purpose of construction. A hole is put through a long straight reed and water is poured into the center. When the flow out of both sides is equal, the reed is level. The device serv ...
), and plumb-bob
A plumb bob, plumb bob level, or plummet, is a weight, usually with a pointed tip on the bottom, suspended from a string and used as a vertical reference line, or plumb-line. It is a precursor to the spirit level and used to establish a vertic ...
. with mechanical machines;such as the wheel
A wheel is a circular component that is intended to rotate on an axle Bearing (mechanical), bearing. The wheel is one of the key components of the wheel and axle which is one of the Simple machine, six simple machines. Wheels, in conjunction wi ...
and axle
An axle or axletree is a central shaft for a rotating wheel or gear. On wheeled vehicles, the axle may be fixed to the wheels, rotating with them, or fixed to the vehicle, with the wheels rotating around the axle. In the former case, bearing ...
that they knew of the characteristic property of the magnetic needle; and were aware that astronomical events occurred in cycles. Chinese of that time had made attempts to classify or extend the rules of arithmetic or geometry which they knew, and to explain the causes of the phenomena with which they were acquainted beforehand. The Chinese independently developed very large and negative number
In mathematics, a negative number represents an opposite. In the real number system, a negative number is a number that is less than zero. Negative numbers are often used to represent the magnitude of a loss or deficiency. A debt that is owed m ...
s, decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers of the Hindu–Arabic numeral ...
s, a place value decimal system, a binary system
A binary system is a system of two astronomical bodies which are close enough that their gravitational attraction causes them to orbit each other around a barycenter ''(also see animated examples)''. More restrictive definitions require that thi ...
, algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics.
Elementary a ...
, geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, and trigonometry
Trigonometry () is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. T ...
.
Chinese mathematics
Mathematics in China emerged independently by the 11th century BCE. The Chinese independently developed a real number system that includes significantly large and negative numbers, more than one numeral system ( base 2 and base 10), algebra, geomet ...
made early contributions, including a place value system
Positional notation (or place-value notation, or positional numeral system) usually denotes the extension to any base of the Hindu–Arabic numeral system (or decimal system). More generally, a positional system is a numeral system in which the ...
. The geometrical theorem known to the ancient Chinese were acquainted was applicable in certain cases (namely the ratio of sides).The area of the square described on the hypotenuse of a right-angled triangle is equal to the sum of the areas of the squares described on the sides It is that geometrical theorems which can be demonstrated in the quasi-experimental way of superposition were also known to them. In arithmetic their knowledge seems to have been confined to the art of calculation by means of the swan-pan
The suanpan (), also spelled suan pan or souanpan) is an abacus of China, Chinese origin first described in a 190 CE book of the Eastern Han Dynasty, namely ''Supplementary Notes on the Art of Figures'' written by Xu Yue. However, the exact de ...
, and the power of expressing the results in writing. Our knowledge of the early attainments of the Chinese, slight though it is, is more complete than in the case of most of their contemporaries. It is thus instructive, and serves to illustrate the fact, that it can be known a nation may possess considerable skill in the applied arts with but our knowledge of the later mathematics on which those arts are founded can be scarce. Knowledge of Chinese mathematics before 254 BC is somewhat fragmentary, and even after this date the manuscript traditions are obscure. Dates centuries before the classical period are generally considered conjectural by Chinese scholars unless accompanied by verified archaeological evidence.
As in other early societies the focus was on astronomy
Astronomy () is a natural science that studies astronomical object, celestial objects and phenomena. It uses mathematics, physics, and chemistry in order to explain their origin and chronology of the Universe, evolution. Objects of interest ...
in order to perfect the agricultural calendar
A calendar is a system of organizing days. This is done by giving names to periods of time, typically days, weeks, months and years. A date is the designation of a single and specific day within such a system. A calendar is also a physi ...
, and other practical tasks, and not on establishing formal systems
A formal system is an abstract structure used for inferring theorems from axioms according to a set of rules. These rules, which are used for carrying out the inference of theorems from axioms, are the logical calculus of the formal system.
A form ...
. The Chinese Board of Mathematics
Mathematics in China emerged independently by the 11th century BCE. The Chinese independently developed a real number system that includes significantly large and negative numbers, more than one numeral system ( base 2 and base 10), algebra, geome ...
duties were confined to the annual preparation of an almanac, the dates and predictions in which it regulated. Ancient Chinese mathematicians did not develop an axiomatic approach, but made advances in algorithm development and algebra. The achievement of Chinese algebra reached its zenith in the 13th century, when Zhu Shijie
Zhu Shijie (, 1249–1314), courtesy name Hanqing (), pseudonym Songting (), was a Chinese mathematician and writer. He was a Chinese mathematician during the Yuan Dynasty. Zhu was born close to today's Beijing. Two of his mathematical works ha ...
invented method of four unknowns.
As a result of obvious linguistic and geographic barriers, as well as content, Chinese mathematics and that of the mathematics of the ancient Mediterranean world are presumed to have developed more or less independently up to the time when ''The Nine Chapters on the Mathematical Art
''The Nine Chapters on the Mathematical Art'' () is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 2nd century CE. This book is one of the earliest sur ...
'' reached its final form, while the ''Writings on Reckoning
The ''Book on Numbers and Computation'' (), or the ''Writings on Reckoning'', is one of the earliest known Chinese mathematical treatises. It was written during the early Western Han dynasty, sometime between 202 BC and 186 BC.Liu et al. (2003), ...
'' and ''Huainanzi
The ''Huainanzi'' is an ancient Chinese text that consists of a collection of essays that resulted from a series of scholarly debates held at the court of Liu An, Prince of Huainan, sometime before 139. The ''Huainanzi'' blends Daoist, Confuci ...
'' are roughly contemporary with classical Greek mathematics. Some exchange of ideas across Asia through known cultural exchanges from at least Roman times is likely. Frequently, elements of the mathematics of early societies correspond to rudimentary results found later in branches of modern mathematics such as geometry or number theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777� ...
. The Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
for example, has been attested to the time of the Duke of Zhou
Dan, Duke Wen of Zhou (), commonly known as the Duke of Zhou (), was a member of the royal family of the early Zhou dynasty who played a major role in consolidating the kingdom established by his elder brother King Wu. He was renowned for acting ...
. Knowledge of Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients that arises in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although ot ...
has also been shown to have existed in China centuries before Pascal
Pascal, Pascal's or PASCAL may refer to:
People and fictional characters
* Pascal (given name), including a list of people with the name
* Pascal (surname), including a list of people and fictional characters with the name
** Blaise Pascal, Fren ...
, such as by Shen Kuo
Shen Kuo (; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁),Yao (2003), 544. was a Chinese polymathic scientist and statesman of the Song dynasty (960–1279). Shen wa ...
.
trigonometry
Trigonometry () is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. T ...
in China slowly began to change and advance during the Song Dynasty (960–1279), where Chinese mathematicians began to express greater emphasis for the need of spherical trigonometry in calendarical science and astronomical calculations. The polymath
A polymath ( el, πολυμαθής, , "having learned much"; la, homo universalis, "universal human") is an individual whose knowledge spans a substantial number of subjects, known to draw on complex bodies of knowledge to solve specific pro ...
Chinese scientist, mathematician and official Shen Kuo
Shen Kuo (; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁),Yao (2003), 544. was a Chinese polymathic scientist and statesman of the Song dynasty (960–1279). Shen wa ...
(1031–1095) used trigonometric functions to solve mathematical problems of chords and arcs.Needham, Joseph (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd.. Sal Restivo writes that Shen's work in the lengths of arcs of circles provided the basis for spherical trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are gr ...
developed in the 13th century by the mathematician and astronomer Guo Shoujing
Guo Shoujing (, 1231–1316), courtesy name Ruosi (), was a Chinese astronomer, hydraulic engineer, mathematician, and politician of the Yuan dynasty. The later Johann Adam Schall von Bell (1591–1666) was so impressed with the preserved astron ...
(1231–1316).Sal Restivo
Sal Restivo (born 1940) is a sociologist/anthropologist.
Work
Restivo is a leading contributor to science studies and in particular to the sociology of mathematics. His current work focuses on the sociology of mind and brain, and the sociology o ...
As the historians L. Gauchet and Joseph Needham state, Guo Shoujing used spherical trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are gr ...
in his calculations to improve the calendar system
A calendar is a system of organizing days. This is done by giving names to periods of time, typically days, weeks, months and years. A calendar date, date is the designation of a single and specific day within such a system. A calendar is ...
and Chinese astronomy
Astronomy in China has a long history stretching from the Shang dynasty, being refined over a period of more than 3,000 years. The ancient Chinese people have identified stars from 1300 BCE, as Chinese star names later categorized in the twe ...
.Needham, Joseph (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd.Marcel Gauchet
Marcel Gauchet (; born 1946) is a French historian, philosopher, and sociologist. He is professor emeritus of the Centre de recherches politiques Raymond Aron at the École des Hautes Études en Sciences Sociales and head of the periodical ''Le D ...
, 151. The mathematical science of the Chinese would incorporate the work and teaching of Arab missionaries with knowledge of spherical trigonometry who had come to China in the course of the thirteenth century.
Indian & Arabic numerals and notation
Although the origin of our present system of numerical notation is ancient, there is no doubt that it was in use among the Hindus over two thousand years ago. The algebraic notation of theIndian mathematician
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics (400 CE to 1200 CE), important contributions were made by scholars like Aryabhata, Brahmagupta, ...
, Brahmagupta
Brahmagupta ( – ) was an Indian mathematician and astronomer. He is the author of two early works on mathematics and astronomy: the ''Brāhmasphuṭasiddhānta'' (BSS, "correctly established doctrine of Brahma", dated 628), a theoretical trea ...
, was syncopated
In music, syncopation is a variety of rhythms played together to make a piece of music, making part or all of a tune or piece of music off-beat. More simply, syncopation is "a disturbance or interruption of the regular flow of rhythm": a "place ...
. Addition was indicated by placing the numbers side by side, subtraction by placing a dot over the subtrahend
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. Subtraction is signified by the minus sign, . For example, in the adjacent picture, there are peaches—meaning 5 peaches with 2 taken ...
(the number to be subtracted), and division by placing the divisor below the dividend, similar to our notation but without the bar. Multiplication, evolution, and unknown quantities were represented by abbreviations of appropriate terms.Boyer, C. B. A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 (1991 pbk ed. ). "China and India" p. 221. (cf., "he was the first one to give a ''general'' solution of the linear Diophantine equation ax + by = c, where a, b, and c are integers. ..It is greatly to the credit of Brahmagupta that he gave ''all'' integral solutions of the linear Diophantine equation, whereas Diophantus himself had been satisfied to give one particular solution of an indeterminate equation. Inasmuch as Brahmagupta used some of the same examples as Diophantus, we see again the likelihood of Greek influence in India – or the possibility that they both made use of a common source, possibly from Babylonia. It is interesting to note also that the algebra of Brahmagupta, like that of Diophantus, was syncopated. Addition was indicated by juxtaposition, subtraction by placing a dot over the subtrahend, and division by placing the divisor below the dividend, as in our fractional notation but without the bar. The operations of multiplication and evolution (the taking of roots), as well as unknown quantities, were represented by abbreviations of appropriate words.") The Hindu–Arabic numeral system
The Hindu–Arabic numeral system or Indo-Arabic numeral system Audun HolmeGeometry: Our Cultural Heritage 2000 (also called the Hindu numeral system or Arabic numeral system) is a positional decimal numeral system, and is the most common syste ...
and the rules for the use of its operations, in use throughout the world today, likely evolved over the course of the first millennium AD in India
India, officially the Republic of India (Hindi: ), is a country in South Asia. It is the seventh-largest country by area, the second-most populous country, and the most populous democracy in the world. Bounded by the Indian Ocean on the so ...
and was transmitted to the west via Islamic mathematics.
 Despite their name,
Despite their name, Arabic numerals
Arabic numerals are the ten numerical digits: , , , , , , , , and . They are the most commonly used symbols to write Decimal, decimal numbers. They are also used for writing numbers in other systems such as octal, and for writing identifiers ...
have roots in India. The reason for this misnomer
A misnomer is a name that is incorrectly or unsuitably applied. Misnomers often arise because something was named long before its correct nature was known, or because an earlier form of something has been replaced by a later form to which the name ...
is Europeans saw the numerals used in an Arabic book, ''Concerning the Hindu Art of Reckoning'', by Mohommed ibn-Musa al-Khwarizmi. Al-Khwārizmī wrote several important books on the Hindu–Arabic numerals and on methods for solving equations. His book ''On the Calculation with Hindu Numerals'', written about 825, along with the work of Al-Kindi
Abū Yūsuf Yaʻqūb ibn ʼIsḥāq aṣ-Ṣabbāḥ al-Kindī (; ar, أبو يوسف يعقوب بن إسحاق الصبّاح الكندي; la, Alkindus; c. 801–873 AD) was an Arab Muslim philosopher, polymath, mathematician, physician ...
,Al-Kindi also introduced cryptanalysis
Cryptanalysis (from the Greek ''kryptós'', "hidden", and ''analýein'', "to analyze") refers to the process of analyzing information systems in order to understand hidden aspects of the systems. Cryptanalysis is used to breach cryptographic sec ...
and frequency analysis
In cryptanalysis, frequency analysis (also known as counting letters) is the study of the frequency of letters or groups of letters in a ciphertext. The method is used as an aid to breaking classical ciphers.
Frequency analysis is based on t ...
. were instrumental in spreading Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics (400 CE to 1200 CE), important contributions were made by scholars like Aryabhata, Brahmagupta ...
and Indian numerals
Indian or Indians may refer to:
Peoples South Asia
* Indian people, people of Indian nationality, or people who have an Indian ancestor
** Non-resident Indian, a citizen of India who has temporarily emigrated to another country
* South Asia ...
to the West. Al-Khwarizmi did not claim the numerals as Arabic, but over several Latin translations, the fact that the numerals were Indian in origin was lost. The word ''algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specificat ...
'' is derived from the Latinization of Al-Khwārizmī's name, Algoritmi, and the word ''algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics.
Elementary a ...
'' from the title of one of his works, '' Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa’l-muqābala'' (''The Compendious Book on Calculation by Completion and Balancing'').
Islamic mathematics
Mathematics during the Golden Age of Islam, especially during the 9th and 10th centuries, was built on Greek mathematics (Euclid, Archimedes, Apollonius) and Indian mathematics (Aryabhata, Brahmagupta). Important progress was made, such as full ...
developed and expanded the mathematics known to Central Asia
Central Asia, also known as Middle Asia, is a subregion, region of Asia that stretches from the Caspian Sea in the west to western China and Mongolia in the east, and from Afghanistan and Iran in the south to Russia in the north. It includes t ...
n civilizations. Al-Khwārizmī gave an exhaustive explanation for the algebraic solution of quadratic equations with positive roots, and Al-Khwārizmī was to teach algebra in an elementary form and for its own sake. Al-Khwārizmī also discussed the fundamental method of " reduction" and "balancing", referring to the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation. This is the operation which al-Khwārizmī originally described as ''al-jabr''.Boyer, C. B. A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 (1991 pbk ed. ). "The Arabic Hegemony" p. 229. (cf., "It is not certain just what the terms ''al-jabr'' and ''muqabalah'' mean, but the usual interpretation is similar to that implied in the translation above. The word ''al-jabr'' presumably meant something like "restoration" or "completion" and seems to refer to the transposition of subtracted terms to the other side of an equation; the word ''muqabalah'' is said to refer to "reduction" or "balancing" – that is, the cancellation of like terms on opposite sides of the equation.") His algebra was also no longer concerned "with a series of problems to be resolved, but an exposition
Exposition (also the French for exhibition) may refer to:
*Universal exposition or World's Fair
*Expository writing
**Exposition (narrative)
*Exposition (music)
*Trade fair
* ''Exposition'' (album), the debut album by the band Wax on Radio
*Exposi ...
which starts with primitive terms in which the combinations must give all possible prototypes for equations, which henceforward explicitly constitute the true object of study." Al-Khwārizmī also studied an equation for its own sake and "in a generic manner, insofar as it does not simply emerge in the course of solving a problem, but is specifically called on to define an infinite class of problems."
Al-Karaji
( fa, ابو بکر محمد بن الحسن الکرجی; c. 953 – c. 1029) was a 10th-century Persian people, Persian mathematician and engineer who flourished at Baghdad. He was born in Karaj, a city near Tehran. His three principal sur ...
, in his treatise ''al-Fakhri'', extends the methodology to incorporate integer powers and integer roots of unknown quantities.Something close to a proof
Proof most often refers to:
* Proof (truth), argument or sufficient evidence for the truth of a proposition
* Alcohol proof, a measure of an alcoholic drink's strength
Proof may also refer to:
Mathematics and formal logic
* Formal proof, a con ...
by mathematical induction
Mathematical induction is a method for proving that a statement ''P''(''n'') is true for every natural number ''n'', that is, that the infinitely many cases ''P''(0), ''P''(1), ''P''(2), ''P''(3), ... all hold. Informal metaphors help ...
appears in a book written by Al-Karaji around 1000 AD, who used it to prove the binomial theorem
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial into a sum involving terms of the form , where the ...
, Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients that arises in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although ot ...
, and the sum of integral
In mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented i ...
cubes
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
The cube is the only r ...
. The historian
A historian is a person who studies and writes about the past and is regarded as an authority on it. Historians are concerned with the continuous, methodical narrative and research of past events as relating to the human race; as well as the stu ...
of mathematics, F. Woepcke, praised Al-Karaji for being "the first who introduced the theory
A theory is a rational type of abstract thinking about a phenomenon, or the results of such thinking. The process of contemplative and rational thinking is often associated with such processes as observational study or research. Theories may be s ...
of algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics.
Elementary a ...
ic calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithm ...
." Also in the 10th century, Abul Wafa translated the works of Diophantus
Diophantus of Alexandria ( grc, Διόφαντος ὁ Ἀλεξανδρεύς; born probably sometime between AD 200 and 214; died around the age of 84, probably sometime between AD 284 and 298) was an Alexandrian mathematician, who was the aut ...
into Arabic. Ibn al-Haytham
Ḥasan Ibn al-Haytham, Latinized as Alhazen (; full name ; ), was a medieval mathematician, astronomer, and physicist of the Islamic Golden Age from present-day Iraq.For the description of his main fields, see e.g. ("He is one of the prin ...
would develop analytic geometry
In classical mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.
Analytic geometry is used in physics and engineerin ...
. Al-Haytham derived the formula for the sum of the fourth powers, using a method that is readily generalizable for determining the general formula for the sum of any integral powers. Al-Haytham performed an integration in order to find the volume of a paraboloid
In geometry, a paraboloid is a quadric surface that has exactly one axis of symmetry and no center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has a similar property of symmetry.
Every plane ...
, and was able to generalize his result for the integrals of polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An exa ...
s up to the fourth degree.He thus came close to finding a general formula for the integral
In mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented i ...
s of polynomials, but he was not concerned with any polynomials higher than the fourth degree. In the late 11th century, Omar Khayyam
Ghiyāth al-Dīn Abū al-Fatḥ ʿUmar ibn Ibrāhīm Nīsābūrī (18 May 1048 – 4 December 1131), commonly known as Omar Khayyam ( fa, عمر خیّام), was a polymath, known for his contributions to mathematics, astronomy, philosophy, an ...
would develop algebraic geometry
Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrical ...
, wrote ''Discussions of the Difficulties in Euclid'',a book about what he perceived as flaws in Euclid's ''Elements'', especially the parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's ''Elements'', is a distinctive axiom in Euclidean geometry. It states that, in two-dimensional geometry:
''If a line segment ...
and wrote on the general geometric solution to cubic equation
In algebra, a cubic equation in one variable is an equation of the form
:ax^3+bx^2+cx+d=0
in which is nonzero.
The solutions of this equation are called roots of the cubic function defined by the left-hand side of the equation. If all of the ...
s. Nasir al-Din Tusi
Muhammad ibn Muhammad ibn al-Hasan al-Tūsī ( fa, محمد ابن محمد ابن حسن طوسی 18 February 1201 – 26 June 1274), better known as Nasir al-Din al-Tusi ( fa, نصیر الدین طوسی, links=no; or simply Tusi in the West ...
(Nasireddin) made advances in spherical trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are gr ...
. Muslim mathematicians during this period include the addition of the decimal point
A decimal separator is a symbol used to separate the integer part from the fractional part of a number written in decimal form (e.g., "." in 12.45). Different countries officially designate different symbols for use as the separator. The choi ...
notation to the Arabic numerals
Arabic numerals are the ten numerical digits: , , , , , , , , and . They are the most commonly used symbols to write Decimal, decimal numbers. They are also used for writing numbers in other systems such as octal, and for writing identifiers ...
.
The modern Arabic numeral
Arabic numerals are the ten numerical digits: , , , , , , , , and . They are the most commonly used symbols to write Decimal, decimal numbers. They are also used for writing numbers in other systems such as octal, and for writing identifiers ...
symbols used around the world first appeared in Islamic North Africa
North Africa, or Northern Africa is a region encompassing the northern portion of the African continent. There is no singularly accepted scope for the region, and it is sometimes defined as stretching from the Atlantic shores of Mauritania in ...
in the 10th century. A distinctive Western Arabic variant of the Eastern Arabic numerals
The Eastern Arabic numerals, also called Arabic-Hindu numerals or Indo–Arabic numerals, are the symbols used to represent numerical digits in conjunction with the Arabic alphabet in the countries of the Mashriq (the east of the Arab world), ...
began to emerge around the 10th century in the Maghreb
The Maghreb (; ar, الْمَغْرِب, al-Maghrib, lit=the west), also known as the Arab Maghreb ( ar, المغرب العربي) and Northwest Africa, is the western part of North Africa and the Arab world. The region includes Algeria, ...
and Al-Andalus
Al-Andalus DIN 31635, translit. ; an, al-Andalus; ast, al-Ándalus; eu, al-Andalus; ber, ⴰⵏⴷⴰⵍⵓⵙ, label=Berber languages, Berber, translit=Andalus; ca, al-Àndalus; gl, al-Andalus; oc, Al Andalús; pt, al-Ândalus; es, ...
(sometimes called ''ghubar'' numerals, though the term is not always accepted), which are the direct ancestor of the modern Arabic numerals used throughout the world.
Many Greek and Arabic texts on mathematics were then translated into Latin, which led to further development of mathematics in medieval Europe. In the 12th century, scholars traveled to Spain and Sicily seeking scientific Arabic texts, including al-Khwārizmī'stranslated into Latin by Robert of Chester
Robert of Chester (Latin: ''Robertus Castrensis'') was an English Arabist of the 12th century. He translated several historically important books from Arabic to Latin, such as:
* '' The Book of the Composition of Alchemy'' (''Liber de composition ...
and the complete text of Euclid's ''Elements''.translated in various versions by Adelard of Bath
Adelard of Bath ( la, Adelardus Bathensis; 1080? 1142–1152?) was a 12th-century English natural philosopher. He is known both for his original works and for translating many important Arabic and Greek scientific works of astrology, astronom ...
, Herman of Carinthia
Herman of Carinthia (1105/1110 – after 1154), also called Hermanus Dalmata or Sclavus Dalmata, Secundus, by his own words born in the "heart of Istria", was a philosopher, astronomer, astrologer, mathematician and translator of Arabic works int ...
, and Gerard of Cremona
Gerard of Cremona (Latin: ''Gerardus Cremonensis''; c. 1114 – 1187) was an Italian translator of scientific books from Arabic into Latin. He worked in Toledo, Kingdom of Castile and obtained the Arabic books in the libraries at Toledo. Some of ...
One of the European books that advocated using the numerals was ''Liber Abaci
''Liber Abaci'' (also spelled as ''Liber Abbaci''; "The Book of Calculation") is a historic 1202 Latin manuscript on arithmetic by Leonardo of Pisa, posthumously known as Fibonacci.
''Liber Abaci'' was among the first Western books to describe ...
'', by Leonardo of Pisa, better known as Fibonacci
Fibonacci (; also , ; – ), also known as Leonardo Bonacci, Leonardo of Pisa, or Leonardo Bigollo Pisano ('Leonardo the Traveller from Pisa'), was an Italian mathematician from the Republic of Pisa, considered to be "the most talented Western ...
. ''Liber Abaci'' is better known for the mathematical problem Fibonacci wrote in it about a population of rabbits. The growth of the population ended up being a Fibonacci sequence
In mathematics, the Fibonacci numbers, commonly denoted , form a integer sequence, sequence, the Fibonacci sequence, in which each number is the sum of the two preceding ones. The sequence commonly starts from 0 and 1, although some authors start ...
, where a term is the sum of the two preceding terms.
Symbolic stage
;Symbols by popular introduction dateplus
Plus may refer to:
Mathematics
* Addition
* +, the mathematical sign
Music
* ''+'' (Ed Sheeran album), (pronounced "plus"), 2011
* ''Plus'' (Cannonball Adderley Quintet album), 1961
* ''Plus'' (Matt Nathanson EP), 2003
* ''Plus'' (Martin Ga ...
"
at:1489 shift:(0,6) text:" minus"
at:1525 shift:(0,17) text:"radical
Radical may refer to:
Politics and ideology Politics
*Radical politics, the political intent of fundamental societal change
*Radicalism (historical), the Radical Movement that began in late 18th century Britain and spread to continental Europe and ...
"
at:1544 shift:(0,28) text:" parenth."
at:1557 shift:(0,39) text:" equals"
at:1618 shift:(0,3) text:"multiply
Multiplication (often denoted by the cross symbol , by the mid-line dot operator , by juxtaposition, or, on computers, by an asterisk ) is one of the four elementary mathematical operations of arithmetic, with the other ones being additi ...
"
at:1628 shift:(0,14) text:" plus-minus"
at:1628 shift:(0,25) text:"proportion
Proportionality, proportion or proportional may refer to:
Mathematics
* Proportionality (mathematics), the property of two variables being in a multiplicative relation to a constant
* Ratio, of one quantity to another, especially of a part compare ...
"
at:1629 shift:(0,36) text:"radical
Radical may refer to:
Politics and ideology Politics
*Radical politics, the political intent of fundamental societal change
*Radicalism (historical), the Radical Movement that began in late 18th century Britain and spread to continental Europe and ...
"
at:1631 shift:(0,47) text:"inequality
Inequality may refer to:
Economics
* Attention inequality, unequal distribution of attention across users, groups of people, issues in etc. in attention economy
* Economic inequality, difference in economic well-being between population groups
* ...
"
at:1636 shift:(0,58) text:"superscript
A subscript or superscript is a character (such as a number or letter) that is set slightly below or above the normal line of type, respectively. It is usually smaller than the rest of the text. Subscripts appear at or below the baseline, whil ...
"
at:1637 shift:(0,69) text:"radical
Radical may refer to:
Politics and ideology Politics
*Radical politics, the political intent of fundamental societal change
*Radicalism (historical), the Radical Movement that began in late 18th century Britain and spread to continental Europe and ...
"
at:1650 shift:(0,80) text:"percent
In mathematics, a percentage (from la, per centum, "by a hundred") is a number or ratio expressed as a fraction of 100. It is often denoted using the percent sign, "%", although the abbreviations "pct.", "pct" and sometimes "pc" are also use ...
"
at:1655 shift:(0,91) text:"infinity
Infinity is that which is boundless, endless, or larger than any natural number. It is often denoted by the infinity symbol .
Since the time of the ancient Greeks, the philosophical nature of infinity was the subject of many discussions amo ...
"
at:1659 shift:(0,102) text:"division
Division or divider may refer to:
Mathematics
*Division (mathematics), the inverse of multiplication
*Division algorithm, a method for computing the result of mathematical division
Military
*Division (military), a formation typically consisting ...
"
at:1670 shift:(0,113) text:Inequality
Inequality may refer to:
Economics
* Attention inequality, unequal distribution of attention across users, groups of people, issues in etc. in attention economy
* Economic inequality, difference in economic well-being between population groups
* ...
"
at:1675 shift:(0,124) text: differential"
at:1675 shift:(0,135) text:integral
In mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented i ...
"
at:1684 shift:(0,146) text: colon"
at:1698 shift:(0,157) text: dot"
at:1718 shift:(0,5) text:slash
Slash may refer to:
* Slash (punctuation), the "/" character
Arts and entertainment Fictional characters
* Slash (Marvel Comics)
* Slash (''Teenage Mutant Ninja Turtles'')
Music
* Harry Slash & The Slashtones, an American rock band
* Nash ...
"
at:1734 shift:(0,15) text:inequality
Inequality may refer to:
Economics
* Attention inequality, unequal distribution of attention across users, groups of people, issues in etc. in attention economy
* Economic inequality, difference in economic well-being between population groups
* ...
"
at:1755 shift:(0,25) text:summation
In mathematics, summation is the addition of a sequence of any kind of numbers, called ''addends'' or ''summands''; the result is their ''sum'' or ''total''. Beside numbers, other types of values can be summed as well: functions, vectors, mat ...
"
at:1768 shift:(0,35) text: proportionality"
at:1770 shift:(0,45) text: differential"
at:1770 shift:(0,55) text:prime
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
"
at:1801 shift:(0,65) text:identity
Identity may refer to:
* Identity document
* Identity (philosophy)
* Identity (social science)
* Identity (mathematics)
Arts and entertainment Film and television
* ''Identity'' (1987 film), an Iranian film
* ''Identity'' (2003 film), ...
"
at:1808 shift:(0,75) text:integral
In mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented i ...
"
at:1808 shift:(0,85) text:factorial
In mathematics, the factorial of a non-negative denoted is the product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times (n-1) \times (n-2) \t ...
"
at:1812 shift:(0,95) text:product
Product may refer to:
Business
* Product (business), an item that serves as a solution to a specific consumer problem.
* Product (project management), a deliverable or set of deliverables that contribute to a business solution
Mathematics
* Produ ...
"
at:1817 shift:(0,105) text:inclusion
Inclusion or Include may refer to:
Sociology
* Social inclusion, aims to create an environment that supports equal opportunity for individuals and groups that form a society.
** Inclusion (disability rights), promotion of people with disabiliti ...
"
at:1841 shift:(0,115) text: abs."
at:1841 shift:(0,125) text: determ."
at:1843 shift:(0,135) text: line matrix"
at:1846 shift:(0,145) text:"nabla Nabla may refer to any of the following:
* the nabla symbol ∇
** the vector differential operator, also called del, denoted by the nabla
* Nabla, tradename of a type of rail fastening system (of roughly triangular shape)
* ''Nabla'' (moth), a ge ...
"
at:1888 shift:(0,17) text:"union
Union commonly refers to:
* Trade union, an organization of workers
* Union (set theory), in mathematics, a fundamental operation on sets
Union may also refer to:
Arts and entertainment
Music
* Union (band), an American rock group
** ''Un ...
~Intersection
In mathematics, the intersection of two or more objects is another object consisting of everything that is contained in all of the objects simultaneously. For example, in Euclidean geometry, when two lines in a plane are not parallel, their i ...
"
at:1890 shift:(0,28) text:"inclusion
Inclusion or Include may refer to:
Sociology
* Social inclusion, aims to create an environment that supports equal opportunity for individuals and groups that form a society.
** Inclusion (disability rights), promotion of people with disabiliti ...
"
at:1893 shift:(0,39) text:"aleph
Aleph (or alef or alif, transliterated ʾ) is the first letter of the Semitic abjads, including Phoenician , Hebrew , Aramaic , Syriac , Arabic ʾ and North Arabian 𐪑. It also appears as South Arabian 𐩱 and Ge'ez .
These letter ...
"
at:1894 shift:(0,50) text:"membership
Member may refer to:
* Military jury, referred to as "Members" in military jargon
* Element (mathematics), an object that belongs to a mathematical set
* In object-oriented programming, a member of a class
** Field (computer science), entries in ...
"
at:1895 shift:(0,61) text:" braces"
at:1895 shift:(0,72) text:" N"
at:1897 shift:(0,83) text:"existential
Existentialism ( ) is a form of philosophical inquiry that explores the problem of human existence and centers on human thinking, feeling, and acting. Existentialist thinkers frequently explore issues related to the meaning, purpose, and value ...
"
at:1902 shift:(0,94) text:"cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and is ...
"
at:1902 shift:(0,105) text:"dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an algebra ...
"
at:1906 shift:(0,116) text:"disjunction
In logic, disjunction is a logical connective typically notated as \lor and read aloud as "or". For instance, the English language sentence "it is raining or it is snowing" can be represented in logic using the disjunctive formula R \lor S ...
"
at:1909 shift:(0,127) text:" parenth. matrix"
at:1913 shift:(0,138) text:" box matrix"
at:1917 shift:(0,149) text:"contour
Contour may refer to:
* Contour (linguistics), a phonetic sound
* Pitch contour
* Contour (camera system), a 3D digital camera system
* Contour, the KDE Plasma 4 interface for tablet devices
* Contour line, a curve along which the function has a ...
"
at:1930 shift:(0,160) text:" Z, "
at:1930 shift:(12,160) text:" Q"
at:1935 shift:(0,171) text:"universals
In metaphysics, a universal is what particular things have in common, namely characteristics or qualities. In other words, universals are repeatable or recurrent entities that can be instantiated or exemplified by many particular things. For exa ...
"
at:1936 shift:(0,182) text:"arrow
An arrow is a fin-stabilized projectile launched by a bow. A typical arrow usually consists of a long, stiff, straight shaft with a weighty (and usually sharp and pointed) arrowhead attached to the front end, multiple fin-like stabilizers c ...
"
at:1939 shift:(0,193) text:"empty
Empty may refer to:
Music Albums
* ''Empty'' (God Lives Underwater album) or the title song, 1995
* ''Empty'' (Nils Frahm album), 2020
* ''Empty'' (Tait album) or the title song, 2001
Songs
* "Empty" (The Click Five song), 2007
* ...
"
at:1939 shift:(0,204) text:" C"
at:1940 shift:(0,215) text:"arrow
An arrow is a fin-stabilized projectile launched by a bow. A typical arrow usually consists of a long, stiff, straight shaft with a weighty (and usually sharp and pointed) arrowhead attached to the front end, multiple fin-like stabilizers c ...
"
at:1960 shift:(0,17) text:" EoP"
at:1960 shift:(3,5) text:" ∎"
at:1962 shift:(0,28) text:"integral
In mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented i ...
"
Early arithmetic and multiplication
The transition to symbolic algebra, where only symbols are used, can first be seen in the work ofIbn al-Banna' al-Marrakushi
Ibn al‐Bannāʾ al‐Marrākushī ( ar, ابن البناء المراكشي), full name: Abu'l-Abbas Ahmad ibn Muhammad ibn Uthman al-Azdi al-Marrakushi () (29 December 1256 – 31 July 1321), was a Moroccan polymath who was active as a math ...
(1256–1321) and Abū al-Ḥasan ibn ʿAlī al-Qalaṣādī (1412–1482). Al-Qalasādī was the last major medieval Mathematics in medieval Islam, Arab algebraist, who improved on the Mathematical notation, algebraic notation earlier used in the Maghreb
The Maghreb (; ar, الْمَغْرِب, al-Maghrib, lit=the west), also known as the Arab Maghreb ( ar, المغرب العربي) and Northwest Africa, is the western part of North Africa and the Arab world. The region includes Algeria, ...
by Ibn al-Banna. In contrast to the syncopated notations of their predecessors, Diophantus
Diophantus of Alexandria ( grc, Διόφαντος ὁ Ἀλεξανδρεύς; born probably sometime between AD 200 and 214; died around the age of 84, probably sometime between AD 284 and 298) was an Alexandrian mathematician, who was the aut ...
and Brahmagupta
Brahmagupta ( – ) was an Indian mathematician and astronomer. He is the author of two early works on mathematics and astronomy: the ''Brāhmasphuṭasiddhānta'' (BSS, "correctly established doctrine of Brahma", dated 628), a theoretical trea ...
, which lacked symbols for Operation (mathematics), mathematical operations, al-Qalasadi's algebraic notation was the first to have symbols for these functions and was thus "the first steps toward the introduction of algebraic symbolism." He represented Table of mathematical symbols, mathematical symbols using characters from the Arabic alphabet.
 The 14th century saw the development of new mathematical concepts to investigate a wide range of problems. The two widely used arithmetic symbols are addition and subtraction, + and −. The plus sign was used by 1360 by Nicole OresmeHis own personal use started around 1351. in his work ''Algorismus proportionum''. It is thought an abbreviation for "et", meaning "and" in Latin, in much the same way the ampersand sign also began as "et". Oresme at the University of Paris and the Italian Giovanni di Casali independently provided graphical demonstrations of the distance covered by a body undergoing uniformly accelerated motion, asserting that the area under the line depicting the constant acceleration and represented the total distance traveled. The minus sign was used in 1489 by Johannes Widmann in ''Mercantile Arithmetic'' or ''Behende und hüpsche Rechenung auff allen Kauffmanschafft,''. Widmann used the minus symbol with the plus symbol, to indicate deficit and surplus, respectively. In ''Summa de arithmetica, Summa de arithmetica, geometria, proportioni e proportionalità'',Summa de Arithmetica: Geometria Proportioni et Proportionalita. ''Tr''. Sum of Arithmetic: Geometry in proportions and proportionality. Luca Pacioli used symbols for plus and minus symbols and contained
The 14th century saw the development of new mathematical concepts to investigate a wide range of problems. The two widely used arithmetic symbols are addition and subtraction, + and −. The plus sign was used by 1360 by Nicole OresmeHis own personal use started around 1351. in his work ''Algorismus proportionum''. It is thought an abbreviation for "et", meaning "and" in Latin, in much the same way the ampersand sign also began as "et". Oresme at the University of Paris and the Italian Giovanni di Casali independently provided graphical demonstrations of the distance covered by a body undergoing uniformly accelerated motion, asserting that the area under the line depicting the constant acceleration and represented the total distance traveled. The minus sign was used in 1489 by Johannes Widmann in ''Mercantile Arithmetic'' or ''Behende und hüpsche Rechenung auff allen Kauffmanschafft,''. Widmann used the minus symbol with the plus symbol, to indicate deficit and surplus, respectively. In ''Summa de arithmetica, Summa de arithmetica, geometria, proportioni e proportionalità'',Summa de Arithmetica: Geometria Proportioni et Proportionalita. ''Tr''. Sum of Arithmetic: Geometry in proportions and proportionality. Luca Pacioli used symbols for plus and minus symbols and contained algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics.
Elementary a ...
.Much of the work originated from Piero della Francesca whom he dict:appropriated, appropriated and dict:purloined, purloined.
In the 15th century, Ghiyath al-Kashi computed the value of Pi, π to the 16th decimal place. Kashi also had an algorithm for calculating ''n''th roots.This was a special case of the methods given many centuries later by Paolo Ruffini (mathematician), Ruffini and William George Horner, Horner. In 1533, Regiomontanus's table of sines and cosines were published. Scipione del Ferro and Niccolò Fontana Tartaglia discovered solutions for cubic equation
In algebra, a cubic equation in one variable is an equation of the form
:ax^3+bx^2+cx+d=0
in which is nonzero.
The solutions of this equation are called roots of the cubic function defined by the left-hand side of the equation. If all of the ...
s. Gerolamo Cardano published them in his 1545 book ''Ars Magna (Gerolamo Cardano), Ars Magna'', together with a solution for the quartic equations, discovered by his student Lodovico Ferrari. The Nth root, radical symbolThat is, . for square root was introduced by Christoph Rudolff.Because, it is thought, it resembled a lowercase "r" (for "radix"). Michael Stifel's important work ''Arithmetica integra'' contained important innovations in mathematical notation. In 1556, Niccolò Fontana Tartaglia, Niccolò Tartaglia used parentheses for precedence grouping. In 1557 Robert Recorde published ''The Whetstone of Witte'' which introduced the equal sign (=), as well as plus and minus signs for the English reader. In 1564, Gerolamo Cardano analyzed game of chance, games of chance beginning the early stages of probability theory. In 1572 Rafael Bombelli published his ''L'Algebra'' in which he showed how to deal with the imaginary number, imaginary quantities that could appear in Cardano's formula for solving cubic equations. Simon Stevin's book ''De Thiende'' ('the art of tenths'), published in Dutch in 1585, contained a systematic treatment of decimal notation, which influenced all later work on the real number system. The New algebra (1591) of François Viète introduced the modern notational manipulation of algebraic expressions. For navigation and accurate maps of large areas, trigonometry
Trigonometry () is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. T ...
grew to be a major branch of mathematics. Bartholomaeus Pitiscus coin the word "trigonometry", publishing his ''Trigonometria'' in 1595.
John Napier is best known as the inventor of logarithmsPublished in Description of the Marvelous Canon of Logarithms and made common the use of the decimal point
A decimal separator is a symbol used to separate the integer part from the fractional part of a number written in decimal form (e.g., "." in 12.45). Different countries officially designate different symbols for use as the separator. The choi ...
in arithmetic and mathematics. After Napier, Edmund Gunter created the logarithmic scales (lines, or rules) upon which slide rules are based, it was William Oughtred who used two such scales sliding by one another to perform direct multiplication and division (mathematics), division; and he is credited as the inventor of the slide rule in 1622. In 1631 Oughtred introduced the multiplication sign (×) his proportionality sign,That is, ∷
and abbreviations ''sin'' and ''cos'' for the sine and cosine functions. Albert Girard also used the abbreviations 'sin', 'cos' and 'tan' for the trigonometric functions in his treatise.
Johannes Kepler was one of the pioneers of the mathematical applications of infinitesimals.see Law of Continuity. René Descartes is credited as the father of analytical geometry, the bridge between algebra and geometry,Using Cartesian coordinates on the plane, the distance between two points (''x''1, ''y''1) and (''x''2, ''y''2) is defined by the formula:which can be viewed as a version of the
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
. crucial to the discovery of infinitesimal calculus and mathematical analysis, analysis. In the 17th century, Descartes introduced Cartesian co-ordinates which allowed the development of analytic geometry.Further steps in abstraction were taken by Lobachevsky, Bolyai, Riemann, and Carl Friedrich Gauss, Gauss who generalised the concepts of geometry to develop non-Euclidean geometry, non-Euclidean geometries. Blaise Pascal influenced mathematics throughout his life. His ''Traité du triangle arithmétique'' ("Treatise on the Arithmetical Triangle") of 1653 described a convenient tabular presentation for binomial coefficients.Now called Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients that arises in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although ot ...
. Pierre de Fermat and Blaise Pascal would investigate probability.For example, the "problem of points". John Wallis introduced the infinity symbol.That is, . He similarly used this notation for infinitesimals.For example, In 1657, Christiaan Huygens published the treatise on probability, ''On Reasoning in Games of Chance''.Original title, "''De ratiociniis in ludo aleae''"
Johann Rahn introduced the division sign (÷, an obelus variant repurposed) and the therefore sign in 1659. William Jones (mathematician), William Jones used π in ''Synopsis palmariorum mathesios'' in 1706 because it is the initial letter of the Greek word perimetron (περιμετρον), which means perimeter in Greek. This usage was popularized in 1737 by Euler. In 1734, Pierre Bouguer used double horizontal bar below the inequality sign.
Derivatives notation: Leibniz and Newton
The study of linear algebra emerged from the study of determinants, which were used to solve systems of linear equations. Calculus had two main systems of notation, each created by one of the creators: that developed by Isaac Newton and the notation developed by Gottfried Leibniz. Leibniz's is the notation used most often today. Newton's was simply a dot or dash placed above the function.For example, the derivative of the function ''x'' would be written as . The second derivative of ''x'' would be written as , etc. In modern usage, this notation generally denotes derivatives of physical quantities with respect to time, and is used frequently in the science ofmechanics
Mechanics (from Ancient Greek: μηχανική, ''mēkhanikḗ'', "of machines") is the area of mathematics and physics concerned with the relationships between force, matter, and motion among physical objects. Forces applied to objects r ...
. Leibniz, on the other hand, used the letter ''d'' as a prefix to indicate differentiation, and introduced the notation representing derivatives as if they were a special type of fraction.For example, the derivative of the function ''x'' with respect to the variable ''t'' in Leibniz's notation would be written as . This notation makes explicit the variable with respect to which the derivative of the function is taken. Leibniz also created the integral symbol.That is, . The symbol is an long s, elongated S, representing the Latin word ''Summa'', meaning "sum". When finding areas under curves, integration is often illustrated by dividing the area into infinitely many tall, thin rectangles, whose areas are added. Thus, the integral symbol is an elongated s, for sum.
High division operators and functions
Letters of the alphabet in this time were to be used as symbols ofquantity
Quantity or amount is a property that can exist as a Counting, multitude or Magnitude (mathematics), magnitude, which illustrate discontinuity (mathematics), discontinuity and continuum (theory), continuity. Quantities can be compared in terms o ...
; and although much diversity existed with respect to the choice of letters, there were to be several Open standard, universally recognized rules in the following history. Here thus in the history of equations the first letters of the alphabet were indicatively known as coefficients, the last letters the dict:unknown, unknown terms (an ''Unknown known#Unknown knowns, incerti ordinis''). In algebraic geometry
Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrical ...
, again, a similar rule was to be observed, the last letters of the alphabet there denoting the variable or current coordinates. Certain letters, such as , , etc., were by consensus gentium, universal consent appropriated as symbols of the frequently occurring numbers Pi, 3.14159 ..., and e (mathematical constant), 2.7182818 ....,See also: List of representations of e etc., and their use in any other acceptation was to be avoided as much as possible. Letters, too, were to be employed as symbols of operation, and with them other previously mentioned arbitrary operation characters. The letters d, , long s, elongated were to be appropriated as operative symbols in the differential calculus and integral calculus, Delta (letter), and Σ in the calculus of differences. In Functional (mathematics), functional notation, a letter, as a symbol of operation, is combined with another which is regarded as a symbol of Quantity#Quantity in mathematics, quantity.Thus denotes the Result, mathematical result of the performance of the operation upon the Mathematical object, subject . If upon this result the same operation were repeated, the new result would be expressed by , or more concisely by , and so on. The quantity itself regarded as the result of the same operation upon some other function; the proper symbol for which is, by analogy, . Thus and are symbols of Multiplicative inverse, inverse operations, the former cancelling the effect of the latter on the subject . and in a similar manner are termed inverse functions.
Beginning in 1718, Thomas Twinin used the Slash (punctuation), division slash (Slash (punctuation), solidus), deriving it from the earlier Arabic horizontal fraction bar. Pierre-Simon Laplace, Pierre-Simon, marquis de Laplace developed the widely used Laplace operator, Laplacian differential operator.That is, In 1750, Gabriel Cramer developed "''Cramer's Rule''" for solving linear systems.
Euler and prime notations
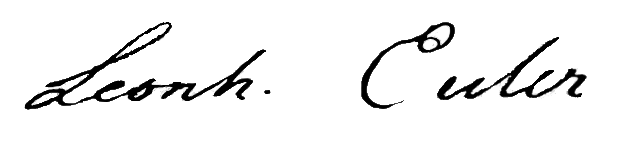 Leonhard Euler was one of the most prolific mathematicians in history, and also a prolific inventor of canonical notation. Contributions of Leonhard Euler to mathematics, His contributions include his use of ''e (mathematical constant), e'' to represent the base of natural logarithms. It is not known exactly why was chosen, but it was probably because the four letters of the alphabet were already commonly used to represent variables and other constants. Euler used to represent pi consistently. The use of was suggested by William Jones (mathematician), William Jones, who used it as shorthand for perimeter. Euler used to represent the square root of negative one,That is, although he earlier used it as an ''infinite number.''Today, the symbol created by John Wallis, , is used for infinity.As in, For
Leonhard Euler was one of the most prolific mathematicians in history, and also a prolific inventor of canonical notation. Contributions of Leonhard Euler to mathematics, His contributions include his use of ''e (mathematical constant), e'' to represent the base of natural logarithms. It is not known exactly why was chosen, but it was probably because the four letters of the alphabet were already commonly used to represent variables and other constants. Euler used to represent pi consistently. The use of was suggested by William Jones (mathematician), William Jones, who used it as shorthand for perimeter. Euler used to represent the square root of negative one,That is, although he earlier used it as an ''infinite number.''Today, the symbol created by John Wallis, , is used for infinity.As in, For summation
In mathematics, summation is the addition of a sequence of any kind of numbers, called ''addends'' or ''summands''; the result is their ''sum'' or ''total''. Beside numbers, other types of values can be summed as well: functions, vectors, mat ...
, Euler used sigma, Capital-sigma notation, Σ.Capital-sigma notation uses a symbol that compactly represents summation of many similar terms: the ''summation symbol'', ''Sigma, Σ'', an enlarged form of the upright capital Greek letter Sigma (letter), Sigma. This is defined as: Where, ''i'' represents the ''index of summation''; ''ai'' is an indexed variable representing each successive term in the series; ''m'' is the ''lower bound of summation'', and ''n'' is the ''upper bound of summation''. The ''"i = m"'' under the summation symbol means that the index ''i'' starts out equal to ''m''. The index, ''i'', is incremented by 1 for each successive term, stopping when ''i'' = ''n''. For function (mathematics), functions, Euler used the notation to represent a function of . In 1730, Euler wrote the gamma function.That is, .
valid for n > 0. In 1736, Euler produced his paper on the Seven Bridges of Königsberg initiating the study of graph theory. The William Emerson (mathematician), mathematician William Emerson would develop the proportionality sign.That is,
∝
Proportionality is the ratio of one quantity to another, especially the ratio of a part compared to a whole. In a mathematical context, a proportion is the statement of equality between two ratios; See Proportionality (mathematics), the relationship of two variables whose ratio is constant. See also aspect ratio, geometric proportions. Much later in the abstract expressions of the value of various proportional phenomena, the parts-per notation would become useful as a set of pseudo units to describe small values of miscellaneous Dimensionless quantity, dimensionless quantities. Marquis de Condorcet, in 1768, advanced the partial differential sign.The ''Curl (mathematics), curly d'' or ''Jacobi's delta''. In 1771, Alexandre-Théophile Vandermonde deduced the importance of topological features when discussing the Knot theory, properties of knots related to the geometry of position. Between 1772 and 1788, Joseph-Louis Lagrange re-formulated the formulas and calculations of Classical "Newtonian" mechanics, called Lagrangian mechanics. The prime symbol for derivatives was also made by Lagrange.
Gauss, Hamilton, and Matrix notations
At the turn of the 19th century, Carl Friedrich Gauss developed the Identity (mathematics), identity sign for congruence relation and, in Quadratic reciprocity, the Floor and ceiling functions, integral part. Gauss contributed function (mathematics), functions of complex variables, ingeometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, and on the convergence of series (mathematics), series. He gave the satisfactory proofs of the fundamental theorem of algebra and of the quadratic reciprocity law. Gauss developed the theory of solving linear systems by using Gaussian elimination, which was initially listed as an advancement in geodesy. He would also develop the product sign. Also in this time, Niels Henrik Abel and Évariste GaloisGalois theory and Galois geometry is named after him. conducted their work on the solvability of equations, linking group theory and Field theory (mathematics), field theory.
After the 1800s, Christian Kramp would promote factorial
In mathematics, the factorial of a non-negative denoted is the product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times (n-1) \times (n-2) \t ...
notation during his research in generalized factorial function which applied to non-integers. Joseph Diaz Gergonne introduced the set inclusion signs.That is, "subset of" and "superset of"; This would later be redeveloped by Ernst Schröder (mathematician), Ernst Schröder. Peter Gustav Lejeune Dirichlet developed Dirichlet L-function, Dirichlet ''L''-functions to give the proof of Dirichlet's theorem on arithmetic progressions and began analytic number theory.A science of numbers that uses methods from mathematical analysis to solve problems about the integers. In 1828, Gauss proved his Theorema Egregium (''remarkable theorem'' in Latin), establishing property of surfaces. In the 1830s, George Green (mathematician), George Green developed Green's function. In 1829. Carl Gustav Jacob Jacobi publishes Fundamenta nova theoriae functionum ellipticarum with his Elliptic function, elliptic theta functions. By 1841, Karl Weierstrass, the "father of modern mathematical analysis, analysis", elaborated on the concept of absolute value and the determinant of a matrix.
Matrix notation would be more fully developed by Arthur Cayley in his three papers, on subjects which had been suggested by reading the Mécanique analytique of Lagrange and some of the works of Laplace. Cayley defined matrix multiplication and matrix inverses. Cayley used a single letter to denote a matrix, thus treating a matrix as an aggregate object. He also realized the connection between matrices and determinants, and wrote "''There would be many things to say about this theory of matrices which should, it seems to me, precede the theory of determinants''".Marie A. Vitulli, Vitulli, Marie. "A Brief History of Linear Algebra and Matrix Theory". Department of Mathematics. University of Oregon. Originally at: darkwing.uoregon.edu/~vitulli/441.sp04/LinAlgHistory.html
William Rowan Hamilton would introduce the nabla symbolThat is, (or, later called ''del'', ∇) for vector differentials. This was previously used by Hamilton as a general-purpose Operator (mathematics), operator sign. Hamilton reformulated Newtonian mechanics, now called Hamiltonian mechanics. This work has proven central to the modern study of classical field theories such as electromagnetism. This was also important to the development of quantum mechanics.See Hamiltonian (quantum mechanics). In mathematics, he is perhaps best known as the inventor of Classical Hamiltonian quaternions, quaternion notationThat is, History of quaternions, and biquaternions. Hamilton also introduced the word "tensor" in 1846.Though his use describes something different from what is now meant by a tensor. Namely, the norm (mathematics), norm operation in a certain type of algebraic system (now known as a Clifford algebra). James Cockle (lawyer), James Cockle would develop the tessarinesThat is,where
and, in 1849, coquaternions. In 1848, James Joseph Sylvester introduced into matrix algebra the term Matrix (mathematics), matrix.This is Latin for "womb".
Maxwell, Clifford, and Ricci notations
 In 1864 James Clerk Maxwell reduced all of the then current knowledge of electromagnetism into a linked set of differential equations with 20 equations in 20 variables, contained in ''A Dynamical Theory of the Electromagnetic Field''. (This article accompanied an 8 December 1864 presentation by Maxwell to the Royal Society.) (See Maxwell's equations.) The method of calculation which it is necessary to employ was given by Lagrange, and afterwards developed, with some modifications, by Hamilton's equations. It is usually referred to as Hamilton's principle; when the equations in the original form are used they are known as Lagrange's equations. In 1871 Richard Dedekind called a set of real or complex numbers which is closed under the four arithmetic operations a field (mathematics), field. In 1873 Maxwell presented ''A Treatise on Electricity and Magnetism''.
In 1878, William Kingdon Clifford published his Elements of Dynamic. Clifford developed split-biquaternions,That is, History of quaternions, which he called ''algebraic motors''. Clifford obviated quaternion study by separating the
In 1864 James Clerk Maxwell reduced all of the then current knowledge of electromagnetism into a linked set of differential equations with 20 equations in 20 variables, contained in ''A Dynamical Theory of the Electromagnetic Field''. (This article accompanied an 8 December 1864 presentation by Maxwell to the Royal Society.) (See Maxwell's equations.) The method of calculation which it is necessary to employ was given by Lagrange, and afterwards developed, with some modifications, by Hamilton's equations. It is usually referred to as Hamilton's principle; when the equations in the original form are used they are known as Lagrange's equations. In 1871 Richard Dedekind called a set of real or complex numbers which is closed under the four arithmetic operations a field (mathematics), field. In 1873 Maxwell presented ''A Treatise on Electricity and Magnetism''.
In 1878, William Kingdon Clifford published his Elements of Dynamic. Clifford developed split-biquaternions,That is, History of quaternions, which he called ''algebraic motors''. Clifford obviated quaternion study by separating the dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an algebra ...
and cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and is ...
of two vectors from the complete quaternion notation.Clifford intersected algebra with Hamilton's quaternions by replacing Hermann Grassmann's rule ''epep'' = 0 by the rule ''epep'' = 1. For more details, see exterior algebra. This approach made vector calculus available to engineers and others working in three dimensions and skeptical of the Phase (waves), lead–lag effectSee: Phasor, Group (mathematics), Signal velocity, Polyphase system, Harmonic oscillator, and RLC series circuit in the Four-dimensional space, fourth dimension.Or the concept of a fourth spatial dimension. See also: Spacetime, the unification of time and space as a four-dimensional Continuum (measurement), continuum; and, Minkowski space, the mathematical setting for special relativity. The common vector notations are used when working with vectors which are vector (geometric), spatial or more abstract members of vector spaces, while angle notation (or phasor (sine waves), phasor notation) is a notation used in electronics.
In 1881, Leopold Kronecker defined what he called a "domain of rationality", which is a field extension of the Field of rationals, field of rational numbers in modern terms. In 1882, wrote the book titled "Linear Algebra". Lord Kelvin's Aether theories, aetheric atomic theory, atom theory (1860s) led Peter Guthrie Tait, in 1885, to publish a topology, topological table of knots with up to ten crossings known as the Tait conjectures. In 1893, Heinrich M. Weber gave the clear definition of an Finite field, abstract field.See also: Field (mathematics), Mathematic fields and Field extension Tensor calculus was developed by Gregorio Ricci-Curbastro between 1887 and 1896, presented in 1892 under the title ''absolute differential calculus'', and the contemporary usage of "tensor" was stated by Woldemar Voigt in 1898. In 1895, Henri Poincaré published ''Analysis Situs (paper), Analysis Situs''. In 1897, Charles Proteus Steinmetz would publish :openlibrary:books/OL7218906M/Theory and calculation of alternating current phenomena, ''Theory and Calculation of Alternating Current Phenomena'', with the assistance of Ernst J. Berg.
From formula mathematics to tensors
In 1895 Giuseppe Peano issued his ''Formulario mathematico'', an effort to digest mathematics into terse text based on special symbols. He would provide a definition of a vector space and linear map. He would also introduce the Intersection (set theory), intersection sign, the union sign, the membership sign (is an element of), and existential quantifierThis raises questions of the existence theorem, pure existence theorems. (there exists). Peano would pass to Bertrand Russell his work in 1900 at a Paris conference; it so impressed Russell that Russell too was taken with the drive to render mathematics more concisely. The result was Principia Mathematica written with Alfred North Whitehead. This treatise marks a watershed in modern literature where symbol became dominant.Peano's ''Formulario Mathematico'', though less popular than Russell's work, continued through five editions. The fifth appeared in 1908 and included 4200 formulas and theorems. Ricci-Curbastro and Tullio Levi-Civita popularized the tensor index notation around 1900.Mathematical logic and abstraction
At the beginning of this period, Felix Klein's "Erlangen program" identified the underlying theme of various geometries, defining each of them as the study of Invariant (mathematics), properties invariant under a given group of Symmetry, symmetries. This level of abstraction revealed connections between geometry and abstract algebra. Georg CantorInventor of set theory would introduce the Aleph number, aleph symbol for cardinal numbers of transfinite sets.''Transfinite arithmetic'' is the generalization of elementary arithmetic to infinity, infinite quantities like infinite sets; See Transfinite numbers, Transfinite induction, and Transfinite interpolation. See also Ordinal arithmetic. His notation for the cardinal numbers was the Hebrew letter (aleph number, aleph) with a natural number subscript; for the ordinals he employed the Greek letter ω (omega). This notation is still in use today in ordinal notation of a finite sequence of symbols from a finite alphabet which names an ordinal number according to some scheme which gives meaning to the language. Cantor's theorem, His theory created a Controversy over Cantor's theory, great deal of controversy. Cantor would, in his study of Fourier series, consider point sets in Euclidean space. After the turn of the 20th century, Josiah Willard Gibbs would in physical chemistry introduce middle dot fordot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an algebra ...
and the multiplication sign for cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and is ...
s. He would also supply notation for the scalar and vector products, which was introduced in ''Vector Analysis (Gibbs/Wilson), Vector Analysis''. In 1904, Ernst Zermelo promotes axiom of choice and his proof of the well-ordering theorem. Bertrand Russell would shortly afterward introduce logical disjunction (Logical disjunction, OR) in 1906. Also in 1906, Poincaré would publish ''On the Dynamics of the Electron'' and Maurice Fréchet introduced metric space. Later, Gerhard Kowalewski and Cuthbert Edmund Cullis would successively introduce matrices notation, parenthetical matrix and box matrix notation respectively. After 1907, mathematiciansSuch as Max Dehn, James Waddell Alexander II, J. W. Alexander, and others. studied knots from the point of view of the knot group and invariants from Homology (mathematics), homology theory.Such as the Alexander polynomial. In 1908, Joseph Wedderburn's structure theorems were formulated for finite-dimensional algebra over a field, algebras over a field. Also in 1908, Ernst Zermelo proposed "definite" property and the first axiomatic set theory, Zermelo set theory. In 1910 Ernst Steinitz published the influential paper ''Algebraic Theory of Fields''.(German: Algebraische Theorie der Körper)In this paper Steinitz axiomatically studied the properties of fields and defined many important field theoretic concepts like prime field, perfect field and the transcendence degree of a field extension. In 1911, Steinmetz would publis''Theory and Calculation of Transient Electric Phenomena and Oscillations''
 Albert Einstein, in 1916, introduced the Einstein notationThe indices range over Set (mathematics), set ,
Albert Einstein, in 1916, introduced the Einstein notationThe indices range over Set (mathematics), set ,is reduced by the convention to:
Upper indices are not Exponentiation, exponents but are indices of coordinates,
coefficient
In mathematics, a coefficient is a multiplicative factor in some term of a polynomial, a series, or an expression; it is usually a number, but may be any expression (including variables such as , and ). When the coefficients are themselves var ...
s or basis vectors.See also: Ricci calculus which summed over a set of index notation, indexed terms in a formula, thus exerting notational brevity. Arnold Sommerfeld would create the contour integral sign in 1917. Also in 1917, Dimitry Mirimanoff proposes axiom of regularity. In 1919, Theodor Kaluza would solve general relativity equations using Five-dimensional space, five dimensions, the results would have electromagnetic equations emerge. This would be published in 1921 in "Zum Unitätsproblem der Physik". In 1922, Abraham Fraenkel and Thoralf Skolem independently proposed replacing the axiom schema of specification with the axiom schema of replacement. Also in 1922, Zermelo–Fraenkel set theory was developed. In 1923, Steinmetz would publis
''Four Lectures on Relativity and Space''
Around 1924, Jan Arnoldus Schouten would develop the modern notation and formalism for the Ricci calculus framework during the absolute differential calculus applications to general relativity and differential geometry in the early twentieth century.Ricci calculus constitutes the rules of index notation and manipulation for tensors and tensor fields. See also: In 1925, Enrico Fermi would describe a Fermi–Dirac statistics, system comprising many identical particles that obey the Pauli exclusion principle, afterwards developing a diffusion equation (Fermi age equation). In 1926, Oskar Klein would develop the Kaluza–Klein theory. In 1928, Emil Artin abstracted ring theory with Artinian rings. In 1933, Andrey Kolmogorov introduces the ''Kolmogorov axioms''. In 1937, Bruno de Finetti deduced the "Coherence (philosophical gambling strategy), operational subjective" concept.
Mathematical symbolism
Mathematical abstraction began as a process of extracting the underlying essence of a mathematical concept, removing any dependence on real world objects with which it might originally have been connected, and generalizing it so that it has wider applications or matching among other abstract descriptions of equivalent phenomena. Two abstract areas of modern mathematics are category theory and model theory. Bertrand Russell, said, "''Ordinary language is totally unsuited for expressing what physics really asserts, since the words of everyday life are not sufficiently abstract. Only mathematics and mathematical logic can say as little as the physicist means to say''". Though, one can substituted mathematics for real world objects, and wander off through equation after equation, and can build a concept structure which has no relation to reality. Symbolic logic studies the purely formal properties of strings of symbols. The interest in this area springs from two sources. First, the notation used in symbolic logic can be seen as representing the words used in philosophical logic. Second, the rules for manipulating symbols found in symbolic logic can be implemented on a computer, computing machine. Symbolic logic is usually divided into two subfields, propositional logic and predicate logic. Other logics of interest include temporal logic, modal logic and fuzzy logic. The area of symbolic logic called propositional logic, also called ''propositional calculus'', studies the properties of sentences formed from logical constant, constantsHere a logical constant is a symbol in symbolic logic that has the same meaning in all models, such as the symbol "=" for "equals".A ''constant'', in a mathematical context, is a Mathematical constant, number that arises naturally in mathematics, such as π or e; Such constant (mathematics), mathematics constant value do not change. It can mean polynomial constant term (the term of degree 0) or the constant of integration, a free parameter arising in integration.
Related, the physical constant are a physical quantity generally believed to be universal and unchanging. Constant (programming), Programming constants are a values that, unlike a variable, cannot be reassociated with a different value. and logical operators. The corresponding logical operations are known, respectively, as logical conjunction, conjunction,
disjunction
In logic, disjunction is a logical connective typically notated as \lor and read aloud as "or". For instance, the English language sentence "it is raining or it is snowing" can be represented in logic using the disjunctive formula R \lor S ...
, material conditional, biconditional, and negation. These operators are denoted as reserved word, keywordsThough not an index term, keywords are terms that represent information. A keyword is a word with special meaning (this is a semantic definition), while syntactically these are terminal symbols in the phrase grammar. See reserved word for the related concept. and by symbolic notation.
Some of the introduced mathematical logic notation during this time included the set of symbols used in Boolean algebra (logic), Boolean algebra. This was created by George Boole in 1854. Boole himself did not see logic as a branch of mathematics, but it has come to be encompassed anyway. Symbols found in Boolean algebra include (AND), (OR), and (''not''). With these symbols, and letters to represent different truth values, one can make logical statements such as , that is "(''a'' is true OR ''a'' is ''not'' true) is true", meaning it is true that ''a'' is either true or not true (i.e. false). Boolean algebra has many practical uses as it is, but it also was the start of what would be a large set of symbols to be used in logic.Most of these symbols can be found in propositional calculus, a formal system described as . is the set of elements, such as the ''a'' in the example with Boolean algebra above. is the set that contains the subsets that contain operations, such as or . contains the inference rules, which are the rules dictating how inferences may be logically made, and contains the axioms. See also: Propositional calculus#propcalc table, Basic and Derived Argument Forms. Predicate logic, originally called ''predicate calculus'', expands on propositional logic by the introduction of Variable (mathematics), variablesUsually denoted by ''x'', ''y'', ''z'', or other lowercase lettersHere a symbols that represents a quantity in a mathematical expression, a Variable (mathematics), mathematical variable as used in many sciences.
Variables can be symbolic name associated with a value and whose associated value may be changed, known in computer science as a Variable (computer science), variable reference. A ''variable'' can also be the operationalization, operationalized way in which the attribute is represented for further data processing (e.g., a logical set of attributes). See also: Dependent and independent variables in statistics. and by sentences containing variables, called Predicate (mathematical logic), predicates.Usually denoted by an uppercase letter followed by a list of variables, such as P(''x'') or Q(''y'',''z'')
Here a Predicate (mathematical logic), mathematical logic predicate, a fundamental concept in first-order logic. Predicate (grammar), Grammatical predicates are grammatical components of a sentence.
Related is the syntactic predicate in parser technology which are guidelines for the parser process. In computer programming, a branch predication allows a choice to execute or not to execute a given instruction based on the content of a machine register. In addition, predicate logic allows Quantifiers (logic), quantifiers.Representing ALL and EXISTS With these logic symbols and additional Quantifier (logic), quantifiers from predicate logic,e.g. ∃ for "there exists" and ∀ for "for all" Validity (logic), valid Mathematical proof, proofs Argumentation theory#Mathematical argumentation, can be made that are Absurdity, irrationally artificial,See also: Dialetheism, Contradiction, and Paradox but syntactical.Related, dict:facetious, facetious abstract nonsense describes certain kinds of arguments and methods related to category theory which resembles comical Non sequitur (literary device), literary non-sequitur devices (not Non sequitur (logic), illogical non-sequiturs).
Gödel incompleteness notation
While proving his incompleteness theorems,Gödel's incompleteness theorems shows that Hilbert's program to find a complete and consistent set of axioms for all mathematics is impossible, giving a contested negative answer to Hilbert's second problem Kurt Gödel created an alternative to the symbols normally used in logic. He used Gödel numbers, which were numbers that represented operations with set numbers, and variables with the prime numbers greater than 10. With Gödel numbers, logic statements can be broken down into a number sequence. Gödel then took this one step farther, taking the ''n'' prime numbers and putting them to the power of the numbers in the sequence. These numbers were then multiplied together to get the final product, giving every logic statement its own number.For example, take the statement "There exists a number ''x'' such that it is not ''y''". Using the symbols of propositional calculus, this would become: .If the Gödel numbers replace the symbols, it becomes:.
There are ten numbers, so the ten prime numbers are found and these are: .
Then, the Gödel numbers are made the powers of the respective primes and multiplied, giving: .
The resulting number is approximately .
Contemporary notation and topics
Early 20th-century notation
Abstraction of notation is an ongoing process and the historical development of many mathematical topics exhibits a progression from the concrete to the abstract. Various set notations would be developed for fundamental object Set (mathematics), sets. Around 1924, David Hilbert and Richard Courant published "Methoden der mathematischen Physik, Methods of mathematical physics. Partial differential equations". In 1926, Oskar Klein and Walter Gordon (physicist), Walter Gordon proposed the Klein–Gordon equation to describe relativistic particles.The Klein–Gordon equation is:The first formulation of a quantum mechanics, quantum theory describing radiation and matter interaction is due to Paul Adrien Maurice Dirac, who, during 1920, was first able to compute the coefficient of spontaneous emission of an atom. In 1928, the relativistic wave equation, relativistic Dirac equation was formulated by Dirac to explain the behavior of the relativistically moving electron.The Dirac equation in the form originally proposed by Dirac is:
where, is the wave function for the electron, and are the space and time coordinates, is the rest mass of the electron, is the momentum, understood to be the momentum operator in the Schrödinger equation, Schrödinger theory, is the speed of light, and is the reduced Planck constant. Dirac described the quantification of the electromagnetic field as an ensemble of harmonic oscillators with the introduction of the concept of creation and annihilation operators of particles. In the following years, with contributions from Wolfgang Pauli, Eugene Wigner, Pascual Jordan, and Werner Heisenberg, and an elegant formulation of quantum electrodynamics due to Enrico Fermi, physicists came to believe that, in principle, it would be possible to perform any computation for any physical process involving photons and charged particles. In 1931, Alexandru Proca developed the Proca equation (Euler–Lagrange equation)That is,
for the vector meson theory of nuclear forces and the relativistic quantum field equations. John Archibald Wheeler in 1937 develops S-matrix. Studies by Felix Bloch with Arnold Nordsieck, and Victor Weisskopf, in 1937 and 1939, revealed that such computations were reliable only at a first order of Perturbation theory (quantum mechanics), perturbation theory, a problem already pointed out by Robert Oppenheimer. At higher orders in the series infinities emerged, making such computations meaningless and casting serious doubts on the internal consistency of the theory itself. With no solution for this problem known at the time, it appeared that a fundamental incompatibility existed between special relativity and quantum mechanics. In the 1930s, the double-struck capital Z for integer number sets was created by Edmund Landau. Nicolas Bourbaki created the double-struck capital Q for rational number sets. In 1935, Gerhard Gentzen made universal quantifiers. In 1936, Tarski's undefinability theorem is stated by Alfred Tarski and proved.The theorem applies more generally to any sufficiently strong formal system, showing that truth in the standard model of the system cannot be defined within the system. In 1938, Kurt Gödel, Gödel proposes the constructible universe in the paper "
The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis
'". André Weil and Nicolas Bourbaki would develop the empty set sign in 1939. That same year, Nathan Jacobson would coin the double-struck capital C for complex number sets. Around the 1930s, Voigt notationNamed to honor Voigt's 1898 work. would be developed for multilinear algebra as a way to represent a symmetric tensor by reducing its order. Schoenflies notation, Schönflies notationNamed after Arthur Moritz Schoenflies became one of two conventions used to describe point groups (the other being Hermann–Mauguin notation). Also in this time, van der Waerden notation became popular for the usage of two-component spinors (Weyl spinors) in four spacetime dimensions. Arend Heyting would introduce Heyting algebra and Heyting arithmetic. The arrow, e.g., →, was developed for function notation in 1936 by Øystein Ore to denote images of specific elements.See Galois connections.Oystein Ore would also write
Number Theory and Its History
. Later, in 1940, it took its present form, e.g., ''f: X → Y'', through the work of Witold Hurewicz. Werner Heisenberg, in 1941, proposed the S-matrix theory of particle interactions.
 Bra–ket notation (Dirac notation) is a standard notation for describing quantum states, composed of bracket, angle brackets and vertical bars. It can also be used to denote abstract vector space, vectors and linear functionals. It is so called because the inner product (or
Bra–ket notation (Dirac notation) is a standard notation for describing quantum states, composed of bracket, angle brackets and vertical bars. It can also be used to denote abstract vector space, vectors and linear functionals. It is so called because the inner product (or dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an algebra ...
on a complex vector space) of two states is denoted by a bra, ket consisting of a left part, ⟨''φ'', , and a right part, , ''ψ''⟩. The notation was introduced in 1939 by Paul Dirac,
though the notation has precursors in Hermann Grassmann, Grassmann's use of the notation [''φ'', ''ψ''] for his inner products nearly 100 years previously.
Bra–ket notation is widespread in quantum mechanics: almost every phenomenon that is explained using quantum mechanics—including a large portion of modern physics—is usually explained with the help of bra–ket notation. The notation establishes an encoded abstract representation-independence, producing a versatile specific representation (e.g., ''x'', or ''p'', or eigenfunction base) without much dict:ado, ado, or excessive reliance on, the Nature (philosophy), nature of the linear spaces involved. The overlap expression ⟨''φ'', ''ψ''⟩ is typically interpreted as the probability amplitude for the Quantum state, state ''ψ'' to wavefunction collapse, collapse into the state ''Φ#Use as a symbol, ϕ''. The Feynman slash notation (Dirac slash notation) was developed by Richard Feynman for the study of Dirac fields in quantum field theory.
In 1948, Valentine Bargmann and Eugene Wigner proposed the relativistic wave equations, relativistic Bargmann–Wigner equations to describe free particles and the equations are in the form of multi-component spinor field wavefunctions. In 1950, W. V. D. Hodge, William Vallance Douglas Hodge presented "Hodge conjecture, The topological invariants of algebraic varieties" at the Proceedings of the International Congress of Mathematicians. Between 1954 and 1957, Eugenio Calabi worked on the Calabi conjecture for Kähler metrics and the development of Calabi–Yau manifolds. In 1957, Tullio Regge formulated the mathematical property of potential scattering in the Schrödinger equation.That the scattering amplitude can be thought of as an analytic function of the angular momentum, and that the position of the poles determine power-law growth rates of the amplitude in the purely mathematical region of large values of the cosine of the scattering angle. Stanley Mandelstam, along with Regge, did the initial development of the Regge theory of strong interaction phenomenology. In 1958, Murray Gell-Mann and Richard Feynman, along with George Sudarshan and Robert Marshak, deduced the chiral, chiral structures of the weak interaction in physics. Geoffrey Chew, along with others, would promote matrix notation for the strong interaction, and the associated Bootstrapping (physics), bootstrap principle, in 1960. In the 1960s, set-builder notation was developed for describing a Set (mathematics), set by stating the properties that its members must satisfy. Also in the 1960s, tensors are abstracted within category theory by means of the concept of monoidal category. Later, multi-index notation eliminates conventional notions used in multivariable calculus, partial differential equations, and the theory of distribution (mathematics), distributions, by abstracting the concept of an integer index notation, index to an ordered tuple of indices.
Modern mathematical notation
In the modern mathematics of special relativity, electromagnetism and Wave, wave theory, the d'Alembert operatorThat is, Also known as the d'Alembertian or wave operator. is the Laplace operator of Minkowski space. The Levi-Civita symbolAlso known as, "permutation symbol" (see: permutation), "antisymmetric symbol" (see: Self-complementary graph, antisymmetric), or "alternating symbol" is used in tensor calculus. After the full Lorentz covariance formulations that were finite at any order in a perturbation series of quantum electrodynamics, Sin-Itiro Tomonaga, Julian Schwinger and Richard Feynman were jointly awarded with a Nobel prize in physics in 1965. Their contributions, and those of Freeman Dyson, were about covariant and gauge invariant formulations of quantum electrodynamics that allow computations of observables at any order of Perturbation theory (quantum mechanics), perturbation theory. Feynman's mathematical technique, based on his Feynman diagram, diagrams, initially seemed very different from the field-theoretic, Operator (physics), operator-based approach of Schwinger and Tomonaga, but Freeman Dyson later showed that the two approaches were equivalent. Renormalization, the need to attach a physical meaning at certain divergences appearing in the theory throughintegral
In mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented i ...
s, has subsequently become one of the fundamental aspects of quantum field theory and has come to be seen as a criterion for a theory's general acceptability. Quantum electrodynamics has served as the model and template for subsequent quantum field theories. Peter Higgs, Jeffrey Goldstone, and others, Sheldon Glashow, Steven Weinberg and Abdus Salam independently showed how the weak nuclear force and quantum electrodynamics could be merged into a single electroweak force. In the late 1960s, the particle zoo was composed of the then known elementary particles before the discovery of quarks.
 John Horton Conway, John Conway would further various notations, including the Conway chained arrow notation, the Conway notation (knot theory), Conway notation of knot theory, and the Conway polyhedron notation. The Coxeter notation system classifies symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter and Norman Johnson (mathematician), Norman Johnson more comprehensively defined it.
Combinatorics, Combinatorial LCF notationDevised by Joshua Lederberg and extended by Harold Scott MacDonald Coxeter, Coxeter and Robert Frucht, Frucht has been developed for the representation of cubic graphs that are Hamiltonian path, Hamiltonian. The cycle notation is the convention for writing down a permutation in terms of its constituent cyclic permutation, cycles. This is also called circular notation and the permutation called a ''cyclic'' or ''circular'' permutation.
John Horton Conway, John Conway would further various notations, including the Conway chained arrow notation, the Conway notation (knot theory), Conway notation of knot theory, and the Conway polyhedron notation. The Coxeter notation system classifies symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M. Coxeter and Norman Johnson (mathematician), Norman Johnson more comprehensively defined it.
Combinatorics, Combinatorial LCF notationDevised by Joshua Lederberg and extended by Harold Scott MacDonald Coxeter, Coxeter and Robert Frucht, Frucht has been developed for the representation of cubic graphs that are Hamiltonian path, Hamiltonian. The cycle notation is the convention for writing down a permutation in terms of its constituent cyclic permutation, cycles. This is also called circular notation and the permutation called a ''cyclic'' or ''circular'' permutation.
Computers and markup notation
In 1931, IBM produces the List of IBM products, IBM 601 Multiplying Punch; it is an electromechanical machine that could read two numbers, up to 8 digits long, from a card and punch their product onto the same card. In 1934, Wallace Eckert used a rigged IBM 601 Multiplying Punch to automate the integration of differential equations. In 1936, Alan Turing publishesOn Computable Numbers, With an Application to the Entscheidungsproblem
.And, in 1938, . John von Neumann, pioneer of the digital computer and of computer science,Among von Neumann's other contributions include the application of operator theory to quantum mechanics, in the development of functional analysis, and on various forms of operator theory. in 1945, writes the unfinished work, incomplete ''First Draft of a Report on the EDVAC''. In 1962, Kenneth E. Iverson developed an integral part notation, which became APL (programming language), APL, for manipulating arrays that he taught to his students, and described in his book ''A Programming Language''. In 1970, Edgar F. Codd proposed relational algebra as a relational model, relational model of data for database query languages. In 1971, Stephen Cook publishes "P versus NP problem, The complexity of theorem proving procedures" In the 1970s within computer architecture, Quote notation was developed for a representing number system of
rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all ration ...
s. Also in this decade, the Z notation (just like the APL (programming language), APL language, long before it) uses many non-ASCII symbols, the specification includes suggestions for rendering the Z notation symbols in ASCII and in LaTeX. There are presently various C mathematical functions (Math.h) and numerical libraries. They are Library (computing), libraries used in software development for performing numerical analysis, numerical calculations. These calculations can be handled by symbolic executions; analyzing a program to determine what inputs cause each part of a program to execute. Mathematica and SymPy are examples of computational software programs based on symbolic mathematics.
Future of mathematical notation
 In the history of mathematical notation, ideographic symbol notation has come full circle with the rise of computer visualization systems. The notations can be applied to abstract visualizations, such as for rendering some projections of a Calabi–Yau manifold, Calabi–Yau manifold. Examples of abstract visualization which properly belong to the mathematical imagination can be found in computer graphics. The need for such models abounds, for example, when the measures for the subject of study are actually random variables and not really ordinary mathematical functions.
In the history of mathematical notation, ideographic symbol notation has come full circle with the rise of computer visualization systems. The notations can be applied to abstract visualizations, such as for rendering some projections of a Calabi–Yau manifold, Calabi–Yau manifold. Examples of abstract visualization which properly belong to the mathematical imagination can be found in computer graphics. The need for such models abounds, for example, when the measures for the subject of study are actually random variables and not really ordinary mathematical functions.
See also
;Main relevance: Abuse of notation, Well-formed formula, Big O notation (L-notation), Dowker notation, Hungarian notation, Infix notation, Positional notation, Polish notation (Reverse Polish notation), Sign-value notation, History of writing numbers ; Numbers and quantities: List of numbers, Irrational number, Irrational and suspected irrational numbers, Euler–Mascheroni constant, γ, Apéry's constant, ζ(3), Square root of 2, , Square root of 3, , Square root of 5, , Golden ratio, φ, Plastic number, ρ, Silver ratio, δ''S'', Feigenbaum constants, α, E (mathematical constant), ''e'', Pi, π, Feigenbaum constants, δ, Physical constants, speed of light, ''c'', vacuum permittivity, ''ε''0, Planck's constant, ''h'', gravitational constant, ''G'', Greek letters used in mathematics, science, and engineering ;General relevance: Order of operations, Scientific notation (Engineering notation), Actuarial notation ;Dot notation: Chemical formula, Chemical notation (Lewis dot notation (Electron dot notation)), Dot-decimal notation ;Arrow notation: Knuth's up-arrow notation, infinitary combinatorics (Arrow notation (Ramsey theory)) ;Geometries: Projective geometry, Affine geometry, Finite geometry ;Lists and outlines: Outline of mathematics (List of mathematics history topics, Mathematics history topics and Lists of mathematics topics, Mathematics topics (List of mathematics categories, Mathematics categories)), List of mathematical theories, Mathematical theories ( List of first-order theories, First-order theories, List of theorems, Theorems and List of disproved mathematical ideas, Disproved mathematical ideas), List of mathematical proofs, Mathematical proofs (List of incomplete proofs, Incomplete proofs), List of mathematical identities, Mathematical identities, List of mathematical series, Mathematical series, List of mathematics reference tables, Mathematics reference tables, List of mathematical logic topics, Mathematical logic topics, List of mathematics-based methods, Mathematics-based methods, List of mathematical functions, Mathematical functions, List of transforms, Transforms and List of operators, Operators, List of points in mathematics, Points in mathematics, List of mathematical shapes, Mathematical shapes, List of knots, Knots (List of prime knots, Prime knots and List of mathematical knots and links, Mathematical knots and links), List of inequalities, Inequalities, Mathematical concepts named after places, List of mathematical topics in classical mechanics, Mathematical topics in classical mechanics, List of mathematical topics in quantum theory, Mathematical topics in quantum theory, List of mathematical topics in relativity, Mathematical topics in relativity, List of string theory topics, String theory topics, List of unsolved problems in mathematics, Unsolved problems in mathematics, List of mathematical jargon, Mathematical jargon, List of mathematical examples, Mathematical examples, List of mathematical abbreviations, Mathematical abbreviations, List of mathematical symbols ;Misc.: Hilbert's problems, Mathematical coincidence, Chess notation, Line notation, Musical notation (Dotted note), Whyte notation, Dice notation, recursive categorical syntax ;People: List of mathematicians, Mathematicians (List of amateur mathematicians, Amateur mathematicians and List of female mathematicians, Female mathematicians), Thomas Bradwardine, Thomas Harriot, Felix Hausdorff, Gaston Julia, Helge von Koch, Paul Lévy (mathematician), Paul Lévy, Aleksandr Lyapunov, Benoit Mandelbrot, Lewis Fry Richardson, Wacław Sierpiński, Saunders Mac Lane, Paul Cohen (mathematician), Paul Cohen, Gottlob Frege, G. S. Carr, Robert Recorde, Bartel Leendert van der Waerden, G. H. Hardy, E. M. Wright, James R. Newman, Carl Gustav Jacob Jacobi, Roger Joseph Boscovich, Eric W. Weisstein, List of mathematical probabilists, Mathematical probabilists, List of statisticians, StatisticiansNotes
References and citations
;General *Florian Cajori (1929) ''A History of Mathematical Notations'', 2 vols. Dover reprint in 1 vol., 1993. . ;CitationsFurther reading
;General:A Short Account of the History of Mathematics
By Walter William Rouse Ball.
A Primer of the History of Mathematics
By Walter William Rouse Ball.
A History of Elementary Mathematics
With Hints on Methods of Teaching. By Florian Cajori.
A History of Elementary Mathematics
By Florian Cajori.
A History of Mathematics
By Florian Cajori.
A Short History of Greek Mathematics
By James Gow (Author), James Gow.
On the Development of Mathematical Thought During the Nineteenth Century
By John Theodore Merz.
A New Mathematical and Philosophical Dictionary
By Peter Barlow.
Historical Introduction to Mathematical Literature
By George Abram Miller
A Brief History of Mathematics
By Karl Fink, Wooster Woodruff Beman, David Eugene Smith
History of Modern Mathematics
By David Eugene Smith.
History of modern mathematics
By David Eugene Smith, Mansfield Merriman. ;Other * Principia Mathematica
Volume 1
Volume 2
By Alfred North Whitehead, Bertrand Russell.
The Mathematical Principles of Natural Philosophy
Volume 1, Issue 1. By Sir Isaac Newton, Andrew Motte, William Davis, John Machin, William Emerson.
General investigations of curved surfaces of 1827 and 1825
By Carl Friedrich Gaus.
External links
Mathematical Notation: Past and Future
files.chem.vt.edu.
Some Common Mathematical Symbols and Abbreviations (with History)
Isaiah Lankham, Bruno Nachtergaele, Anne Schilling. {{History of science History of mathematics, Mathematical notation Mathematical notation Articles which contain graphical timelines