|
Well-defined
In mathematics, a well-defined expression or unambiguous expression is an expression (mathematics), expression whose definition assigns it a unique interpretation or value. Otherwise, the expression is said to be ''not well defined'', ill defined or ''ambiguous''. A function is well defined if it gives the same result when the representation of the input is changed without changing the value of the input. For instance, if f takes real numbers as input, and if f(0.5) does not equal f(1/2) then f is not well defined (and thus not a function). The term ''well-defined'' can also be used to indicate that a logical expression is unambiguous or uncontradictory. A function that is not well defined is not the same as a function that is undefined (mathematics), undefined. For example, if f(x)=\frac, then even though f(0) is undefined, this does not mean that the function is ''not'' well defined; rather, 0 is not in the Domain of a function, domain of f. Example Let A_0,A_1 be sets, let A = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expression (mathematics)
In mathematics, an expression is a written arrangement of symbol (mathematics), symbols following the context-dependent, syntax (logic), syntactic conventions of mathematical notation. Symbols can denote numbers, variable (mathematics), variables, operation (mathematics), operations, and function (mathematics), functions. Other symbols include punctuation marks and bracket (mathematics), brackets, used for Symbols of grouping, grouping where there is not a well-defined order of operations. Expressions are commonly distinguished from ''mathematical formula, formulas'': expressions are a kind of mathematical object, whereas formulas are statements ''about'' mathematical objects. This is analogous to natural language, where a noun phrase refers to an object, and a whole Sentence (linguistics), sentence refers to a fact. For example, 8x-5 is an expression, while the Inequality (mathematics), inequality 8x-5 \geq 3 is a formula. To ''evaluate'' an expression means to find a numeric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subtraction
Subtraction (which is signified by the minus sign, –) is one of the four Arithmetic#Arithmetic operations, arithmetic operations along with addition, multiplication and Division (mathematics), division. Subtraction is an operation that represents removal of objects from a collection. For example, in the adjacent picture, there are peaches—meaning 5 peaches with 2 taken away, resulting in a total of 3 peaches. Therefore, the ''difference'' of 5 and 2 is 3; that is, . While primarily associated with natural numbers in arithmetic, subtraction can also represent removing or decreasing physical and abstract quantities using different kinds of objects including negative numbers, Fraction (mathematics), fractions, irrational numbers, Euclidean vector, vectors, decimals, functions, and matrices. In a sense, subtraction is the inverse of addition. That is, if and only if . In words: the difference of two numbers is the number that gives the first one when added to the second one. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniqueness
Uniqueness is a state or condition wherein someone or something is unlike anything else in comparison, or is remarkable, or unusual. When used in relation to humans, it is often in relation to a person's personality, or some specific characteristics of it, signalling that it is unlike the personality traits that are prevalent in that individual's culture. When the term ''uniqueness'' is used in relation to an object, it is often within the realm of product, with the term being a factor used to publicize or market the product in order to make it stand out from other products within the same category. The notion of American exceptionalism is premised on the uniqueness of the West, particularly its well-defined secularism. See also * Loner *Scarcity In economics, scarcity "refers to the basic fact of life that there exists only a finite amount of human and nonhuman resources which the best technical knowledge is capable of using to produce only limited maximum amounts of each e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pathological (mathematics)
In mathematics, when a mathematical phenomenon runs counter to some intuition, then the phenomenon is sometimes called pathological. On the other hand, if a phenomenon does not run counter to intuition, it is sometimes called well-behaved or nice. These terms are sometimes useful in mathematical research and teaching, but there is no strict mathematical definition of pathological or well-behaved. In analysis A classic example of a pathology is the Weierstrass function, a function that is continuous everywhere but differentiable nowhere. The sum of a differentiable function and the Weierstrass function is again continuous but nowhere differentiable; so there are at least as many such functions as differentiable functions. In fact, using the Baire category theorem, one can show that continuous functions are generically nowhere differentiable. Such examples were deemed pathological when they were first discovered. To quote Henri Poincaré: Since Poincaré, nowhere differe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Representative (mathematics)
In mathematics, when the elements of some set S have a notion of equivalence (formalized as an equivalence relation), then one may naturally split the set S into equivalence classes. These equivalence classes are constructed so that elements a and b belong to the same equivalence class if, and only if, they are equivalent. Formally, given a set S and an equivalence relation \sim on S, the of an element a in S is denoted /math> or, equivalently, to emphasize its equivalence relation \sim, and is defined as the set of all elements in S with which a is \sim-related. The definition of equivalence relations implies that the equivalence classes form a partition of S, meaning, that every element of the set belongs to exactly one equivalence class. The set of the equivalence classes is sometimes called the quotient set or the quotient space of S by \sim, and is denoted by S /. When the set S has some structure (such as a group operation or a topology) and the equivalence rel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Definitionism
Definitionism (also called the classical theory of concepts) is the school of thought in which it is believed that a proper explanation of a theory consists of all the concepts used by that theory being well-defined. This approach has been criticized for its dismissal of the importance of ostensive definition An ostensive definition conveys the meaning of a term by pointing out examples. This type of definition is often used where the term is difficult to define verbally, either because the words will not be understood (as with children and new speake ...s. References Definition Epistemology of science Epistemological theories Concepts in the philosophy of science {{epistemology-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Operation (mathematics)
In mathematics, an operation is a function from a set to itself. For example, an operation on real numbers will take in real numbers and return a real number. An operation can take zero or more input values (also called "'' operands''" or "arguments") to a well-defined output value. The number of operands is the arity of the operation. The most commonly studied operations are binary operations (i.e., operations of arity 2), such as addition and multiplication, and unary operations (i.e., operations of arity 1), such as additive inverse and multiplicative inverse. An operation of arity zero, or nullary operation, is a constant. The mixed product is an example of an operation of arity 3, also called ternary operation. Generally, the arity is taken to be finite. However, infinitary operations are sometimes considered, in which case the "usual" operations of finite arity are called finitary operations. A partial operation is defined similarly to an operatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
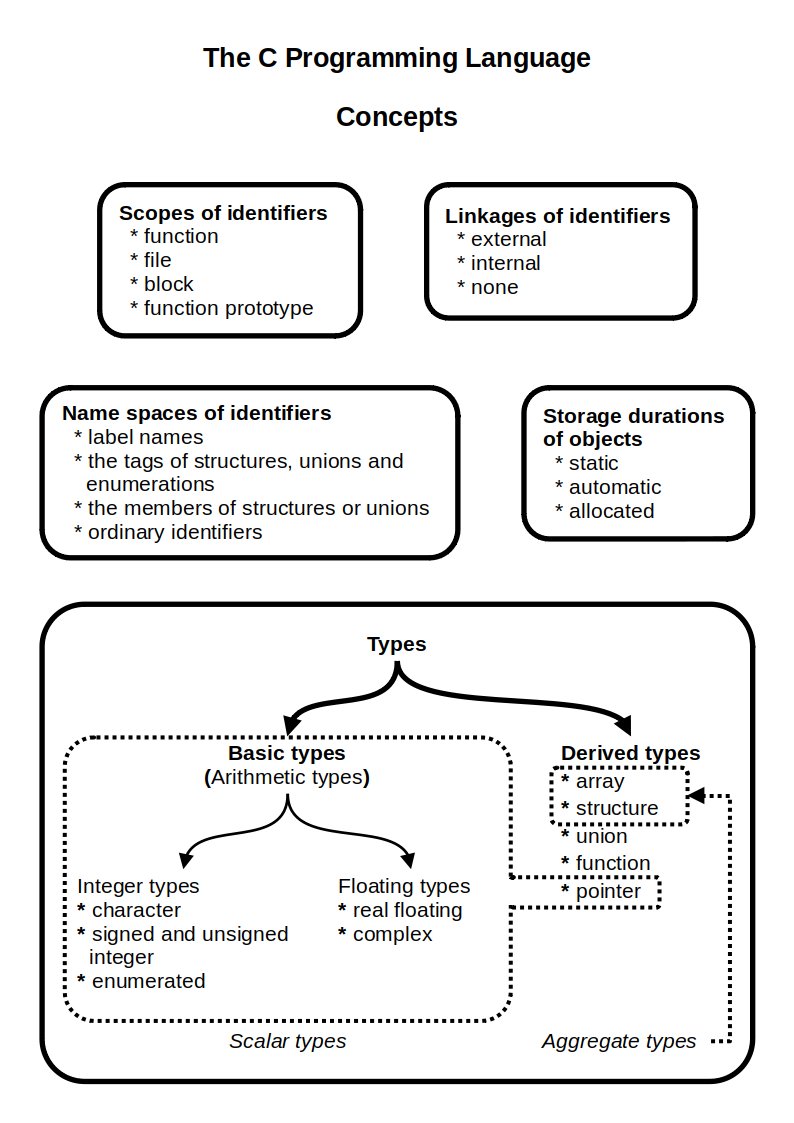
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Well-formed Formula
In mathematical logic, propositional logic and predicate logic, a well-formed formula, abbreviated WFF or wff, often simply formula, is a finite sequence of symbols from a given alphabet that is part of a formal language. The abbreviation wff is pronounced "woof", or sometimes "wiff", "weff", or "whiff". A formal language can be identified with the set of formulas in the language. A formula is a syntactic object that can be given a semantic meaning by means of an interpretation. Two key uses of formulas are in propositional logic and predicate logic. Introduction A key use of formulas is in propositional logic and predicate logic such as first-order logic. In those contexts, a formula is a string of symbols φ for which it makes sense to ask "is φ true?", once any free variables in φ have been instantiated. In formal logic, proofs can be represented by sequences of formulas with certain properties, and the final formula in the sequence is what is proven. Alth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Undefined (mathematics)
In mathematics, the term undefined refers to a value, function, or other expression that cannot be assigned a meaning within a specific formal system. Attempting to assign or use an undefined value within a particular formal system, may produce contradictory or meaningless results within that system. In practice, mathematicians may use the term ''undefined'' to warn that a particular calculation or property can produce mathematically inconsistent results, and therefore, it should be avoided. Caution must be taken to avoid the use of such undefined values in a deduction or proof. Whether a particular function or value is undefined, depends on the rules of the formal system in which it is used. For example, the imaginary number \sqrt is undefined within the set of real numbers. So it is meaningless to reason about the value, solely within the discourse of real numbers. However, defining the imaginary number i to be equal to \sqrt, allows there to be a consistent set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniqueness Quantification
In mathematics and logic, the term "uniqueness" refers to the property of being the one and only object satisfying a certain condition. This sort of quantification is known as uniqueness quantification or unique existential quantification, and is often denoted with the symbols " ∃!" or "∃=1". It is defined to mean there exists an object with the given property, and all objects with this property are equal. For example, the formal statement : \exists! n \in \mathbb\,(n - 2 = 4) may be read as "there is exactly one natural number n such that n - 2 =4". Proving uniqueness The most common technique to prove the unique existence of an object is to first prove the existence of the entity with the desired condition, and then to prove that any two such entities (say, ''a'' and ''b'') must be equal to each other (i.e. a = b). For example, to show that the equation x + 2 = 5 has exactly one solution, one would first start by establishing that at least one solution exists ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Existence
Existence is the state of having being or reality in contrast to nonexistence and nonbeing. Existence is often contrasted with essence: the essence of an entity is its essential features or qualities, which can be understood even if one does not know whether the entity exists. Ontology is the philosophical discipline studying the nature and types of existence. Singular existence is the existence of individual entities while general existence refers to the existence of concepts or universals. Entities present in space and time have Abstract and concrete, concrete existence in contrast to abstract entities, like numbers and sets. Other distinctions are between Subjunctive possibility, possible, Contingency (philosophy), contingent, and Metaphysical necessity, necessary existence and between Matter, physical and Mind, mental existence. The common view is that an entity either exists or not with nothing in between, but some philosophers say that there are degrees of existence, me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |