Ecological Theories

Theoretical ecology is the scientific discipline devoted to the study of ecological systems using theoretical methods such as simple conceptual models, mathematical models, computational simulations, and advanced data analysis. Effective models improve understanding of the natural world by revealing how the dynamics of species populations are often based on fundamental biological conditions and processes. Further, the field aims to unify a diverse range of empirical observations by assuming that common, mechanistic processes generate observable phenomena across species and ecological environments. Based on biologically realistic assumptions, theoretical ecologists are able to uncover novel, non-intuitive insights about natural processes. Theoretical results are often verified by empirical and observational studies, revealing the power of theoretical methods in both predicting and understanding the noisy, diverse biological world.

The field is broad and includes foundations in applied mathematics, computer science, biology, statistical physics, genetics, chemistry, evolution, and conservation biology. Theoretical ecology aims to explain a diverse range of phenomena in the life sciences, such as population growth and dynamics, fisheries, competition, evolutionary theory, epidemiology, animal behavior and group dynamics, food webs, ecosystems, spatial ecology, and the effects of climate change.

Theoretical ecology has further benefited from the advent of fast computing power, allowing the analysis and visualization of large-scale computational simulations of ecological phenomena. Importantly, these modern tools provide quantitative predictions about the effects of human induced environmental change on a diverse variety of ecological phenomena, such as: species invasions, climate change, the effect of fishing and hunting on food network stability, and the global carbon cycle.

Modelling approaches

As in most other sciences, mathematical models form the foundation of modern ecological theory.
* Phenomenological models: distill the functional and distributional shapes from observed patterns in the data, or researchers decide on functions and distribution that are flexible enough to match the patterns they or others (field or experimental ecologists) have found in the field or through experimentation.Bolker BM (2008
''Ecological models and data in R''
Princeton University Press, pages 6–9. .
* Mechanistic models: model the underlying processes directly, with functions and distributions that are based on theoretical reasoning about ecological processes of interest.

Ecological models can be deterministic or stochastic.

* Deterministic models always evolve in the same way from a given starting point. They represent the average, expected behavior of a system, but lack random variation. Many system dynamics models are deterministic.
* Stochastic models allow for the direct modeling of the random perturbations that underlie real world ecological systems. Markov chain models are stochastic.

Species can be modelled in continuous or discrete time.Soetaert K and Herman PMJ (2009
''A practical guide to ecological modelling''
Springer. .

* Continuous time is modelled using differential equations.
* Discrete time is modelled using difference equations. These model ecological processes that can be described as occurring over discrete time steps. Matrix algebra is often used to investigate the evolution of age-structured or stage-structured populations. The Leslie matrix, for example, mathematically represents the discrete time change of an age structured population.

Models are often used to describe real ecological reproduction processes of single or multiple species.
These can be modelled using stochastic branching processes. Examples are the dynamics of interacting populations (predation competition and mutualism), which, depending on the species of interest, may best be modeled over either continuous or discrete time. Other examples of such models may be found in the field of mathematical epidemiology where the dynamic relationships that are to be modeled are host–pathogen interactions.

Bifurcation theory is used to illustrate how small changes in parameter values can give rise to dramatically different long run outcomes, a mathematical fact that may be used to explain drastic ecological differences that come about in qualitatively very similar systems. Logistic maps are polynomial mappings, and are often cited as providing archetypal examples of how chaotic behaviour can arise from very simple non-linear dynamical equations. The maps were popularized in a seminal 1976 paper by the theoretical ecologist Robert May. The difference equation is intended to capture the two effects of reproduction and starvation.

In 1930, R.A. Fisher published his classic ''The Genetical Theory of Natural Selection'', which introduced the idea that frequency-dependent fitness brings a strategic aspect to evolution, where the payoffs to a particular organism, arising from the interplay of all of the relevant organisms, are the number of this organism' s viable offspring. In 1961, Richard Lewontin applied game theory to evolutionary biology in his ''Evolution and the Theory of Games'',
followed closely by John Maynard Smith, who in his seminal 1972 paper, “Game Theory and the Evolution of Fighting", defined the concept of the evolutionarily stable strategy.

Because ecological systems are typically nonlinear, they often cannot be solved analytically and in order to obtain sensible results, nonlinear, stochastic and computational techniques must be used. One class of computational models that is becoming increasingly popular are the agent-based models. These models can simulate the actions and interactions of multiple, heterogeneous, organisms where more traditional, analytical techniques are inadequate. Applied theoretical ecology yields results which are used in the real world. For example, optimal harvesting theory draws on optimization techniques developed in economics, computer science and operations research, and is widely used in fisheries.

Population ecology

Population ecology is a sub-field of ecology that deals with the dynamics of species populations and how these populations interact with the environment. It is the study of how the population sizes of species living together in groups change over time and space, and was one of the first aspects of ecology to be studied and modelled mathematically.

Exponential growth

The most basic way of modeling population dynamics is to assume that the rate of growth of a population depends only upon the population size at that time and the per capita growth rate of the organism. In other words, if the number of individuals in a population at a time t, is N(t), then the rate of population growth is given by:
:$\frac=rN(t)$
where r is the per capita growth rate, or the intrinsic growth rate of the organism. It can also be described as r = b-d, where b and d are the per capita time-invariant birth and death rates, respectively. This first order linear differential equation can be solved to yield the solution
:$N(t) = N(0) \ e^$,
a trajectory known as Malthusian growth, after Thomas Malthus, who first described its dynamics in 1798. A population experiencing Malthusian growth follows an exponential curve, where N(0) is the initial population size. The population grows when r > 0, and declines when r < 0. The model is most applicable in cases where a few organisms have begun a colony and are rapidly growing without any limitations or restrictions impeding their growth (e.g. bacteria inoculated in rich media).

Logistic growth

The exponential growth model makes a number of assumptions, many of which often do not hold. For example, many factors affect the intrinsic growth rate and is often not time-invariant. A simple modification of the exponential growth is to assume that the intrinsic growth rate varies with population size. This is reasonable: the larger the population size, the fewer resources available, which can result in a lower birth rate and higher death rate. Hence, we can replace the time-invariant r with r’(t) = (b –a*N(t)) – (d + c*N(t)), where a and c are constants that modulate birth and death rates in a population dependent manner (e.g. intraspecific competition). Both a and c will depend on other environmental factors which, we can for now, assume to be constant in this approximated model. The differential equation is now:Moss R, Watson A and Ollason J (1982
''Animal population dynamics''
Springer, page 52–54. .
:$\frac=((b-aN(t))-(d-cN(t)))N(t)$
This can be rewritten as:
:$\frac=rN(t) \left(1-\frac\right)$
where r = b-d and K = (b-d)/(a+c).

The biological significance of K becomes apparent when stabilities of the equilibria of the system are considered. The constant K is the carrying capacity of the population. The equilibria of the system are N = 0 and N = K. If the system is linearized, it can be seen that N = 0 is an unstable equilibrium while K is a stable equilibrium.

Structured population growth

Another assumption of the exponential growth model is that all individuals within a population are identical and have the same probabilities of surviving and of reproducing. This is not a valid assumption for species with complex life histories. The exponential growth model can be modified to account for this, by tracking the number of individuals in different age classes (e.g. one-, two-, and three-year-olds) or different stage classes (juveniles, sub-adults, and adults) separately, and allowing individuals in each group to have their own survival and reproduction rates.
The general form of this model is
:$\mathbf_ = \mathbf\mathbf_t$
where N_t is a vector of the number of individuals in each class at time ''t'' and L is a matrix that contains the survival probability and fecundity for each class. The matrix L is referred to as the Leslie matrix for age-structured models, and as the Lefkovitch matrix for stage-structured models.

If parameter values in L are estimated from demographic data on a specific population, a structured model can then be used to predict whether this population is expected to grow or decline in the long-term, and what the expected age distribution within the population will be. This has been done for a number of species including loggerhead sea turtles and right whales.

Community ecology

An ecological community is a group of trophically similar, sympatric species that actually or potentially compete in a local area for the same or similar resources. Interactions between these species form the first steps in analyzing more complex dynamics of ecosystems. These interactions shape the distribution and dynamics of species. Of these interactions, predation is one of the most widespread population activities.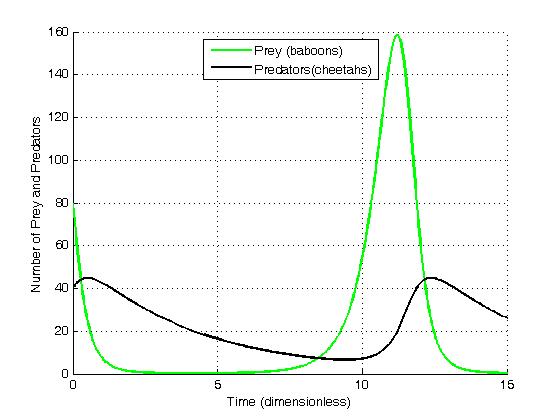
Taken in its most general sense, predation comprises predator–prey, host–pathogen, and host–parasitoid interactions.

Predator–prey interaction

Predator–prey interactions exhibit natural oscillations in the populations of both predator and the prey. In 1925, the American mathematician Alfred J. Lotka developed simple equations for predator–prey interactions in his book on biomathematics. The following year, the Italian mathematician Vito Volterra, made a statistical analysis of fish catches in the AdriaticGoel, N.S. et al., "On the Volterra and Other Non-Linear Models of Interacting Populations", ''Academic Press Inc.'', (1971) and independently developed the same equations. It is one of the earliest and most recognised ecological models, known as the Lotka-Volterra model:

:$\frac = N(t)(r-\alpha P(t))$
:$\frac = P(t)(c \alpha N(t) -d)$
where N is the prey and P is the predator population sizes, r is the rate for prey growth, taken to be exponential in the absence of any predators, α is the prey mortality rate for per-capita predation (also called ‘attack rate’), c is the efficiency of conversion from prey to predator, and d is the exponential death rate for predators in the absence of any prey.

Volterra originally used the model to explain fluctuations in fish and shark populations after fishing was curtailed during the First World War. However, the equations have subsequently been applied more generally. Other examples of these models include the Lotka-Volterra model of the snowshoe hare and Canadian lynx in North America, any infectious disease modeling such as the recent outbreak of SARS

and biological control of California red scale by the introduction of its parasitoid, '' Aphytis melinus''
.

A credible, simple alternative to the Lotka-Volterra predator–prey model and their common prey dependent generalizations is the ratio dependent or Arditi-Ginzburg model. The two are the extremes of the spectrum of predator interference models. According to the authors of the alternative view, the data show that true interactions in nature are so far from the Lotka–Volterra extreme on the interference spectrum that the model can simply be discounted as wrong. They are much closer to the ratio-dependent extreme, so if a simple model is needed one can use the Arditi–Ginzburg model as the first approximation.

Host–pathogen interaction

The second interaction, that of host and pathogen, differs from predator–prey interactions in that pathogens are much smaller, have much faster generation times, and require a host to reproduce. Therefore, only the host population is tracked in host–pathogen models. Compartmental models that categorize host population into groups such as susceptible, infected, and recovered (SIR) are commonly used.

Host–parasitoid interaction

The third interaction, that of host and parasitoid, can be analyzed by the Nicholson–Bailey model, which differs from Lotka-Volterra and SIR models in that it is discrete in time. This model, like that of Lotka-Volterra, tracks both populations explicitly. Typically, in its general form, it states:
: N_ = \lambda \ N_t \ 1 - f(N_t, P_t) /math>
:$P_ = c \ N_t \ f(N_t, p_t)$
where f(N_t, P_t) describes the probability of infection (typically, Poisson distribution), λ is the per-capita growth rate of hosts in the absence of parasitoids, and c is the conversion efficiency, as in the Lotka-Volterra model.

Competition and mutualism

In studies of the populations of two species, the Lotka-Volterra system of equations has been extensively used to describe dynamics of behavior between two species, N₁ and N₂. Examples include relations between '' D. discoiderum'' and '' E. coli'',
as well as theoretical analysis of the behavior of the system.
:$\frac = \frac\left( K_1 - N_1 + \alpha_N_2 \right)$
:$\frac = \frac\left( K_2 - N_2 + \alpha_N_1 \right)$
The r coefficients give a “base” growth rate to each species, while K coefficients correspond to the carrying capacity. What can really change the dynamics of a system, however are the α terms. These describe the nature of the relationship between the two species. When α₁₂ is negative, it means that N₂ has a negative effect on N₁, by competing with it, preying on it, or any number of other possibilities. When α₁₂ is positive, however, it means that N₂ has a positive effect on N₁, through some kind of mutualistic interaction between the two.
When both α₁₂ and α₂₁ are negative, the relationship is described as competitive. In this case, each species detracts from the other, potentially over competition for scarce resources.
When both α₁₂ and α₂₁ are positive, the relationship becomes one of mutualism. In this case, each species provides a benefit to the other, such that the presence of one aids the population growth of the other.

:''See Competitive Lotka–Volterra equations for further extensions of this model.''

Neutral theory

Unified neutral theory is a hypothesis proposed by Stephen P. Hubbell in 2001. The hypothesis aims to explain the diversity and relative abundance of species in ecological communities, although like other neutral theories in ecology, Hubbell's hypothesis assumes that the differences between members of an ecological community of trophically similar species are "neutral," or irrelevant to their success. Neutrality means that at a given trophic level in a food web, species are equivalent in birth rates, death rates, dispersal rates and speciation rates, when measured on a per-capita basis. This implies that biodiversity arises at random, as each species follows a random walk. This can be considered a null hypothesis to niche theory. The hypothesis has sparked controversy, and some authors consider it a more complex version of other null models that fit the data better.

Under unified neutral theory, complex ecological interactions are permitted among individuals of an ecological community (such as competition and cooperation), providing all individuals obey the same rules. Asymmetric phenomena such as parasitism and predation are ruled out by the terms of reference; but cooperative strategies such as swarming, and negative interaction such as competing for limited food or light are allowed, so long as all individuals behave the same way. The theory makes predictions that have implications for the management of biodiversity, especially the management of rare species. It predicts the existence of a fundamental biodiversity constant, conventionally written ''θ'', that appears to govern species richness on a wide variety of spatial and temporal scales.

Hubbell built on earlier neutral concepts, including MacArthur & Wilson's theory of island biogeography and Gould's concepts of symmetry and null models.

Spatial ecology

Biogeography

Biogeography is the study of the distribution of species in space and time. It aims to reveal where organisms live, at what abundance, and why they are (or are not) found in a certain geographical area.

Biogeography is most keenly observed on islands, which has led to the development of the subdiscipline of island biogeography. These habitats are often a more manageable areas of study because they are more condensed than larger ecosystems on the mainland. In 1967, Robert MacArthur and E.O. Wilson published ''The Theory of Island Biogeography''. This showed that the species richness in an area could be predicted in terms of factors such as habitat area, immigration rate and extinction rate. The theory is considered one of the fundamentals of ecological theory. The application of island biogeography theory to habitat fragments spurred the development of the fields of conservation biology and landscape ecology.

r/K-selection theory

A population ecology concept is r/K selection theory, one of the first predictive models in ecology used to explain life-history evolution. The premise behind the r/K selection model is that natural selection pressures change according to population density. For example, when an island is first colonized, density of individuals is low. The initial increase in population size is not limited by competition, leaving an abundance of available resources for rapid population growth. These early phases of population growth experience ''density-independent'' forces of natural selection, which is called ''r''-selection. As the population becomes more crowded, it approaches the island's carrying capacity, thus forcing individuals to compete more heavily for fewer available resources. Under crowded conditions, the population experiences density-dependent forces of natural selection, called ''K''-selection.

Niche theory

Metapopulations

Spatial analysis of ecological systems often reveals that assumptions that are valid for spatially homogenous populations – and indeed, intuitive – may no longer be valid when migratory subpopulations moving from one patch to another are considered. In a simple one-species formulation, a subpopulation may occupy a patch, move from one patch to another empty patch, or die out leaving an empty patch behind. In such a case, the proportion of occupied patches may be represented as
:$\frac = m p (1-p) - e p$
where m is the rate of colonization, and e is the rate of extinction. In this model, if e < m, the steady state value of p is 1 – (e/m) while in the other case, all the patches will eventually be left empty. This model may be made more complex by addition of another species in several different ways, including but not limited to game theoretic approaches, predator–prey interactions, etc. We will consider here an extension of the previous one-species system for simplicity. Let us denote the proportion of patches occupied by the first population as p₁, and that by the second as p₂. Then,
:$\frac = m_1 p_1 (1 - p_1) - e p_1$
:$\frac = m_2 p_2 (1 - p_1 - p_2) - e p_2 - m p_1 p_2$
In this case, if e is too high, p₁ and p₂ will be zero at steady state. However, when the rate of extinction is moderate, p₁ and p₂ can stably coexist. The steady state value of p₂ is given by
:$p^*_2 = \frac - \frac$
(p*₁ may be inferred by symmetry).
If e is zero, the dynamics of the system favor the species that is better at colonizing (i.e. has the higher m value). This leads to a very important result in theoretical ecology known as the Intermediate Disturbance Hypothesis, where the biodiversity (the number of species that coexist in the population) is maximized when the disturbance (of which e is a proxy here) is not too high or too low, but at intermediate levels.

The form of the differential equations used in this simplistic modelling approach can be modified. For example:
# Colonization may be dependent on p linearly (m*(1-p)) as opposed to the non-linear m*p*(1-p) regime described above. This mode of replication of a species is called the “rain of propagules”, where there is an abundance of new individuals entering the population at every generation. In such a scenario, the steady state where the population is zero is usually unstable.Vandermeer JH and Goldberg DE (2003
''Population ecology: first principles''
Princeton University Press, page 175–176. .
# Extinction may depend non-linearly on p (e*p*(1-p)) as opposed to the linear (e*p) regime described above. This is referred to as the “rescue effect” and it is again harder to drive a population extinct under this regime.

The model can also be extended to combinations of the four possible linear or non-linear dependencies of colonization and extinction on p are described in more detail in.

Ecosystem ecology

Introducing new elements, whether biotic or abiotic, into ecosystems can be disruptive. In some cases, it leads to ecological collapse, trophic cascades and the death of many species within the ecosystem. The abstract notion of ecological health attempts to measure the robustness and recovery capacity for an ecosystem; i.e. how far the ecosystem is away from its steady state. Often, however, ecosystems rebound from a disruptive agent. The difference between collapse or rebound depends on the toxicity of the introduced element and the resiliency of the original ecosystem.

If ecosystems are governed primarily by stochastic processes, through which its subsequent state would be determined by both predictable and random actions, they may be more resilient to sudden change than each species individually. In the absence of a balance of nature, the species composition of ecosystems would undergo shifts that would depend on the nature of the change, but entire ecological collapse would probably be infrequent events. In 1997, Robert Ulanowicz used information theory tools to describe the structure of ecosystems, emphasizing mutual information (correlations) in studied systems. Drawing on this methodology and prior observations of complex ecosystems, Ulanowicz depicts approaches to determining the stress levels on ecosystems and predicting system reactions to defined types of alteration in their settings (such as increased or reduced energy flow, and eutrophication.

Ecopath is a free ecosystem modelling software suite, initially developed by NOAA, and widely used in fisheries management as a tool for modelling and visualising the complex relationships that exist in real world marine ecosystems.

Food webs

Food webs provide a framework within which a complex network of predator–prey interactions can be organised. A food web model is a network of food chains. Each food chain starts with a primary producer or autotroph, an organism, such as a plant, which is able to manufacture its own food. Next in the chain is an organism that feeds on the primary producer, and the chain continues in this way as a string of successive predators. The organisms in each chain are grouped into trophic levels, based on how many links they are removed from the primary producers. The length of the chain, or trophic level, is a measure of the number of species encountered as energy or nutrients move from plants to top predators. Food energy flows from one organism to the next and to the next and so on, with some energy being lost at each level. At a given trophic level there may be one species or a group of species with the same predators and prey.

In 1927, Charles Elton published an influential synthesis on the use of food webs, which resulted in them becoming a central concept in ecology. In 1966, interest in food webs increased after Robert Paine's experimental and descriptive study of intertidal shores, suggesting that food web complexity was key to maintaining species diversity and ecological stability. Many theoretical ecologists, including Sir Robert May and Stuart Pimm, were prompted by this discovery and others to examine the mathematical properties of food webs. According to their analyses, complex food webs should be less stable than simple food webs. The apparent paradox between the complexity of food webs observed in nature and the mathematical fragility of food web models is currently an area of intensive study and debate. The paradox may be due partially to conceptual differences between persistence of a food web and equilibrial stability of a food web.May RM (2001
''Stability and Complexity in Model Ecosystems''
Princeton University Press, reprint of 1973 edition with new foreword. .Pimm SL (2002
''Food Webs''
University of Chicago Press, reprint of 1982 edition with new foreword. .

Systems ecology

Systems ecology can be seen as an application of general systems theory to ecology. It takes a holistic and interdisciplinary approach to the study of ecological systems, and particularly ecosystems. Systems ecology is especially concerned with the way the functioning of ecosystems can be influenced by human interventions. Like other fields in theoretical ecology, it uses and extends concepts from thermodynamics and develops other macroscopic descriptions of complex systems. It also takes account of the energy flows through the different trophic levels in the ecological networks. Systems ecology also considers the external influence of ecological economics, which usually is not otherwise considered in ecosystem ecology. For the most part, systems ecology is a subfield of ecosystem ecology.

Ecophysiology

This is the study of how "the environment, both physical and biological, interacts with the physiology of an organism. It includes the effects of climate and nutrients on physiological processes in both plants and animals, and has a particular focus on how physiological processes scale with organism size".

Behavioral ecology

Swarm behaviour

Swarm behaviour is a collective behaviour exhibited by animals of similar size which aggregate together, perhaps milling about the same spot or perhaps migrating in some direction. Swarm behaviour is commonly exhibited by insects, but it also occurs in the flocking of birds, the schooling of fish and the herd behaviour of quadrupeds. It is a complex emergent behaviour that occurs when individual agents follow simple behavioral rules.

Recently, a number of mathematical models have been discovered which explain many aspects of the emergent behaviour. Swarm algorithms follow a Lagrangian approach or an Eulerian approach. The Eulerian approach views the swarm as a field, working with the density of the swarm and deriving mean field properties. It is a hydrodynamic approach, and can be useful for modelling the overall dynamics of large swarms. However, most models work with the Lagrangian approach, which is an agent-based model following the individual agents (points or particles) that make up the swarm. Individual particle models can follow information on heading and spacing that is lost in the Eulerian approach. Examples include ant colony optimization, self-propelled particles and particle swarm optimization

Evolutionary ecology

The British biologist Alfred Russel Wallace is best known for independently proposing a theory of evolution due to natural selection that prompted Charles Darwin to publish his own theory. In his famous 1858 paper, Wallace proposed natural selection as a kind of feedback mechanism which keeps species and varieties adapted to their environment.

''The action of this principle is exactly like that of the centrifugal governor of the steam engine, which checks and corrects any irregularities almost before they become evident; and in like manner no unbalanced deficiency in the animal kingdom can ever reach any conspicuous magnitude, because it would make itself felt at the very first step, by rendering existence difficult and extinction almost sure soon to follow.''

The cybernetician and anthropologist Gregory Bateson observed in the 1970s that, though writing it only as an example, Wallace had "probably said the most powerful thing that’d been said in the 19th Century". Subsequently, the connection between natural selection and systems theory has become an area of active research.

Other theories

In contrast to previous ecological theories which considered floods to be catastrophic events, the river flood pulse concept argues that the annual flood pulse is the most important aspect and the most biologically productive feature of a river's ecosystem.Thorp, J. H., & Delong, M. D. (1994). The Riverine Productivity Model: An Heuristic View of Carbon Sources and Organic Processing in Large River Ecosystems. Oikos , 305-308Benke, A. C., Chaubey, I., Ward, G. M., & Dunn, E. L. (2000). Flood Pulse Dynamics of an Unregulated River Floodplain in the Southeastern U.S. Coastal Plain. Ecology , 2730-2741.

History

Theoretical ecology draws on pioneering work done by G. Evelyn Hutchinson and his students. Brothers H.T. Odum and E.P. Odum are generally recognised as the founders of modern theoretical ecology. Robert MacArthur brought theory to community ecology. Daniel Simberloff was the student of E.O. Wilson, with whom MacArthur collaborated on ''The Theory of Island Biogeography'', a seminal work in the development of theoretical ecology.Cuddington K and Beisner BE (2005
''Ecological paradigms lost: routes of theory change''
Academic Press. .

Simberloff added statistical rigour to experimental ecology and was a key figure in the SLOSS debate, about whether it is preferable to protect a single large or several small reserves. This resulted in the supporters of Jared Diamond's community assembly rules defending their ideas through Neutral Model Analysis. Simberloff also played a key role in the (still ongoing) debate on the utility of corridors for connecting isolated reserves.

Stephen P. Hubbell and Michael Rosenzweig combined theoretical and practical elements into works that extended MacArthur and Wilson's Island Biogeography Theory - Hubbell with his Unified Neutral Theory of Biodiversity and Biogeography and Rosenzweig with his Species Diversity in Space and Time.

Theoretical and mathematical ecologists

A tentative distinction can be made between mathematical ecologists, ecologists who apply mathematics to ecological problems, and mathematicians who develop the mathematics itself that arises out of ecological problems.

Some notable theoretical ecologists can be found in these categories:

* :Mathematical ecologists
* :Theoretical biologists

Journals

* ''The American Naturalist''
* ''Journal of Mathematical Biology''
* ''Journal of Theoretical Biology''
*
Theoretical Ecology
'
*
Theoretical Population Biology
'
*
Ecological Modelling
'

See also

* Butterfly effect
* Complex system biology
* Ecological systems theory
* Ecosystem model
* Integrodifference equation – widely used to model the dispersal and growth of populations
* Limiting similarity
* Mathematical biology
* Population dynamics
* Population modeling
* Quantitative ecology
* Taylor's law
* Theoretical biology

References

Further reading

* The classic text is ''Theoretical Ecology: Principles and Applications'', by Angela McLean and Robert May. The 2007 edition is published by the Oxford University Press. .

----

* Bolker BM (2008
''Ecological Models and Data in R''
Princeton University Press. .
* Case TJ (2000
''An illustrated guide to theoretical ecology''
Oxford University Press. .
* Caswell H (2000) ''Matrix Population Models: Construction, Analysis, and Interpretation'', Sinauer, 2nd Ed. .
* Edelstein-Keshet L (2005
''Mathematical Models in Biology''
Society for Industrial and Applied Mathematics. .
* Gotelli NJ (2008
''A Primer of Ecology''
Sinauer Associates, 4th Ed. .
* Gotelli NJ & A Ellison (2005
''A Primer Of Ecological Statistics''
Sinauer Associates Publishers. .
* Hastings A (1996
''Population Biology: Concepts and Models''
Springer. .
* Hilborn R & M Clark (1997
''The Ecological Detective: Confronting Models with Data''
Princeton University Press.
* Kokko H (2007
''Modelling for field biologists and other interesting people''
Cambridge University Press. .
* Kot M (2001
''Elements of Mathematical Ecology''
Cambridge University Press. .
*
* Murray JD (2002
''Mathematical Biology, Volume 1''
Springer, 3rd Ed. .
* Murray JD (2003
''Mathematical Biology, Volume 2''
Springer, 3rd Ed. .
* Pastor J (2008
''Mathematical Ecology of Populations and Ecosystems''
Wiley-Blackwell. .
* Roughgarden J (1998
''Primer of Ecological Theory''
Prentice Hall. .
* Ulanowicz R (1997
''Ecology: The Ascendant Perspective''
Columbia University Press.

{{DEFAULTSORT:Theoretical ecology

*
Ecology