|
Theoretical Ecology
Theoretical ecology is the scientific discipline devoted to the study of ecological systems using theoretical methods such as simple conceptual models, mathematical models, computational simulations, and advanced data analysis. Effective models improve understanding of the natural world by revealing how the dynamics of species populations are often based on fundamental biological conditions and processes. Further, the field aims to unify a diverse range of empirical observations by assuming that common, mechanistic processes generate observable phenomena across species and ecological environments. Based on biologically realistic assumptions, theoretical ecologists are able to uncover novel, non-intuitive insights about natural processes. Theoretical results are often verified by empirical and observational studies, revealing the power of theoretical methods in both predicting and understanding the noisy, diverse biological world. The field is broad and includes foundations in appli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology. Mainly the study of differential equations consists of the study of their solutions (the set of functions that satisfy each equation), and of the properties of their solutions. Only the simplest differential equations are solvable by explicit formulas; however, many properties of solutions of a given differential equation may be determined without computing them exactly. Often when a closed-form expression for the solutions is not available, solutions may be approximated numerically using computers. The theory of d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robert May, Baron May Of Oxford
Robert McCredie May, Baron May of Oxford, HonFAIB (8 January 1936 – 28 April 2020) was an Australian scientist who was Chief Scientific Adviser to the UK Government, President of the Royal Society, and a professor at the University of Sydney and Princeton University. He held joint professorships at the University of Oxford and Imperial College London. He was also a crossbench member of the House of Lords from 2001 until his retirement in 2017. May was a Fellow of Merton College, Oxford, and an appointed member of the council of the British Science Association. He was also a member of the advisory council for the Campaign for Science and Engineering. Early life and education May was born in Sydney on 8 January 1936, to lawyer Henry Wilkinson May and Kathleen Mitchell (née McCredie), who divorced when he was seven years old. His father was of prosperous middle-class Northern Irish origin, and his mother was the daughter of a Scottish engineer. May was educated at Sydney Boys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-linear
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists because most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems. Typically, the behavior of a nonlinear system is described in mathematics by a nonlinear system of equations, which is a set of simultaneous equations in which the unknowns (or the unknown functions in the case of differential equations) appear as variables of a polynomial of degree higher than one or in the argument of a function which is not a polynomial of degree one. In other words, in a nonlinear system of equations, the equation(s) to be solved cannot be written as a linear combination of the un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaos Theory
Chaos theory is an interdisciplinary area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions, and were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning that there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause a tornado in Texas. Small differences in initial conditions, such as those due to errors in measurements or due to rounding errors i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial Map
In algebra, a polynomial map or polynomial mapping P: V \to W between vector spaces over an infinite field ''k'' is a polynomial in linear functionals with coefficients in ''k''; i.e., it can be written as :P(v) = \sum_ \lambda_(v) \cdots \lambda_(v) w_ where the \lambda_: V \to k are linear functionals and the w_ are vectors in ''W''. For example, if W = k^m, then a polynomial mapping can be expressed as P(v) = (P_1(v), \dots, P_m(v)) where the P_i are (scalar-valued) polynomial functions on ''V''. (The abstract definition has an advantage that the map is manifestly free of a choice of basis.) When ''V'', ''W'' are finite-dimensional vector spaces and are viewed as algebraic varieties, then a polynomial mapping is precisely a morphism of algebraic varieties. One fundamental outstanding question regarding polynomial mappings is the Jacobian conjecture, which concerns the sufficiency of a polynomial mapping to be invertible. See also *Polynomial functor References *Claudio Pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
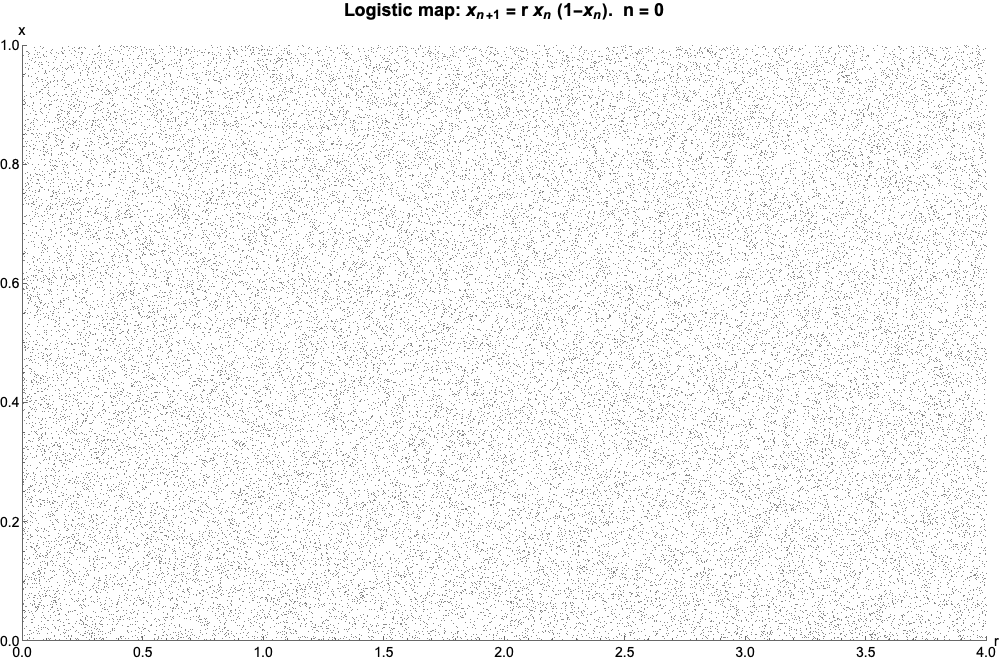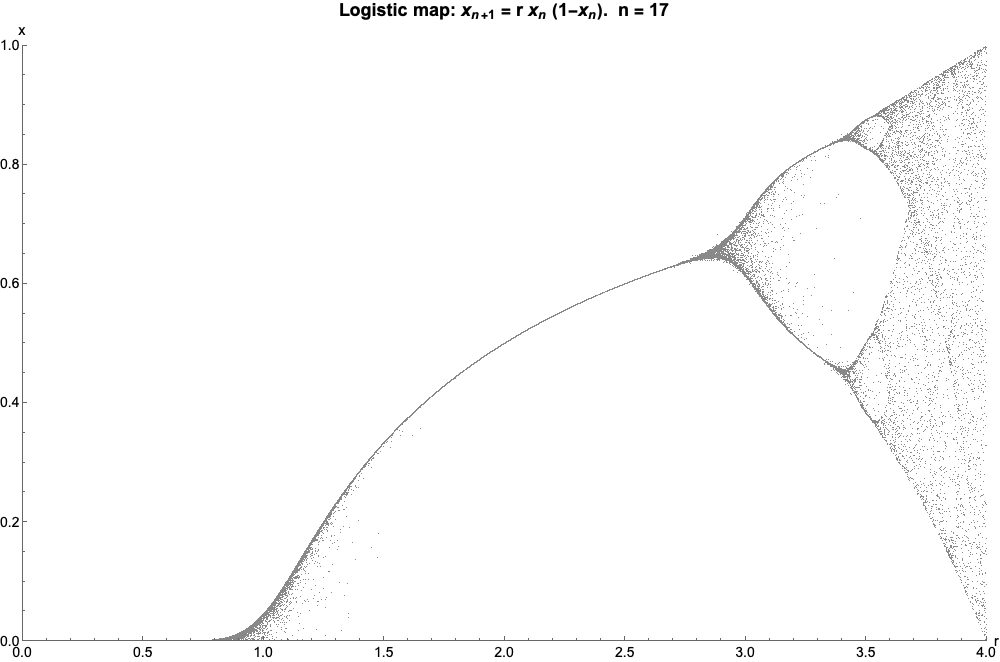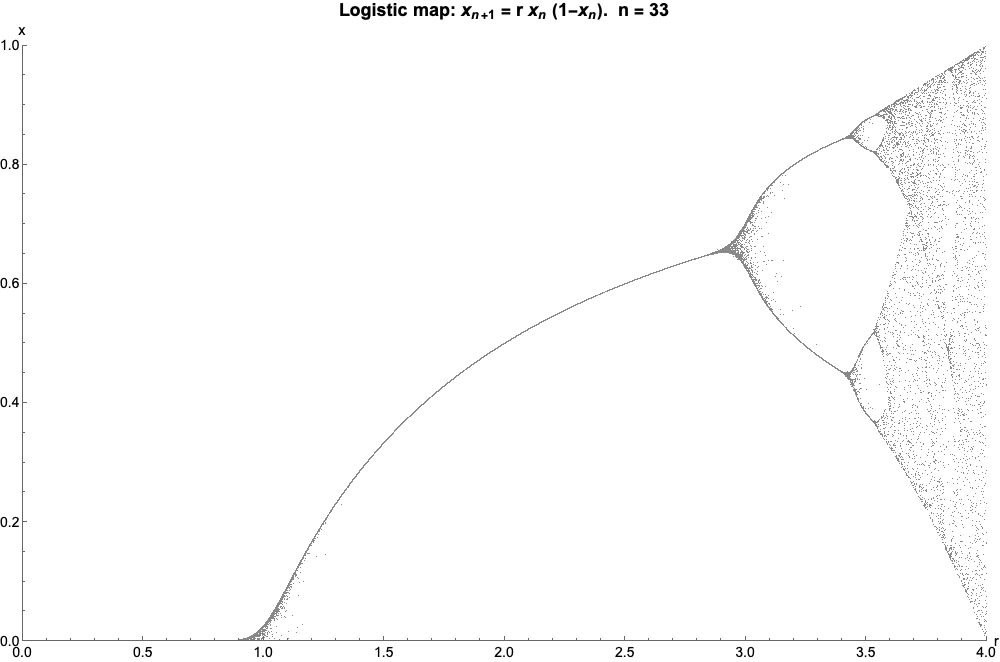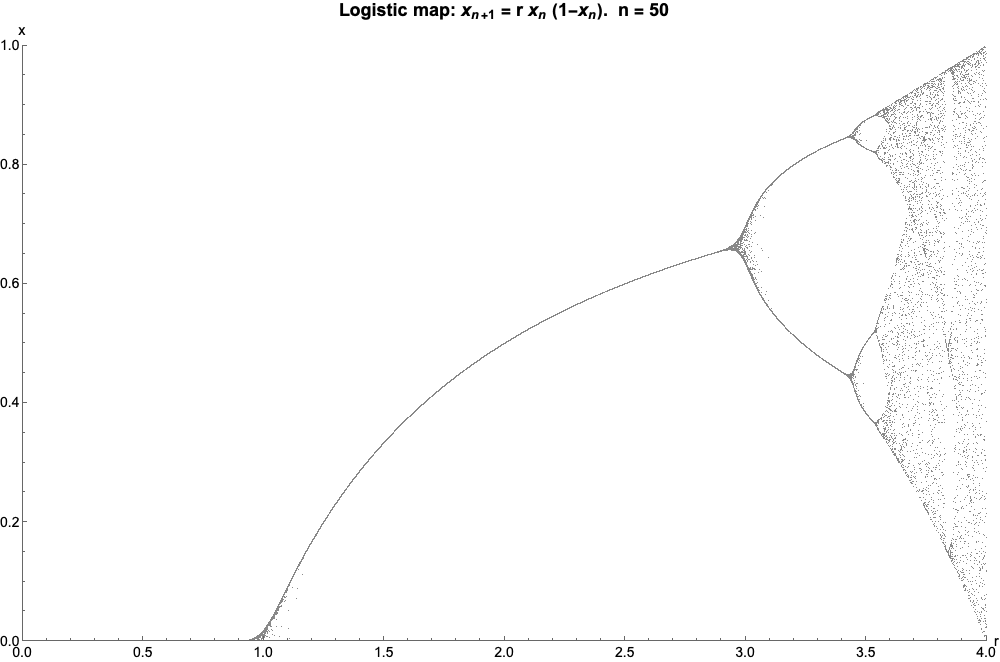
Logistic Map
The logistic map is a polynomial mapping (equivalently, recurrence relation) of degree 2, often referred to as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations. The map was popularized in a 1976 paper by the biologist Robert May, in part as a discrete-time demographic model analogous to the logistic equation written down by Pierre François Verhulst. Mathematically, the logistic map is written where is a number between zero and one, that represents the ratio of existing population to the maximum possible population. This nonlinear difference equation is intended to capture two effects: * ''reproduction'' where the population will increase at a rate proportional to the current population when the population size is small. * ''starvation'' (density-dependent mortality) where the growth rate will decrease at a rate proportional to the value obtained by taking the theoretical "carrying capacity" of the environment l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
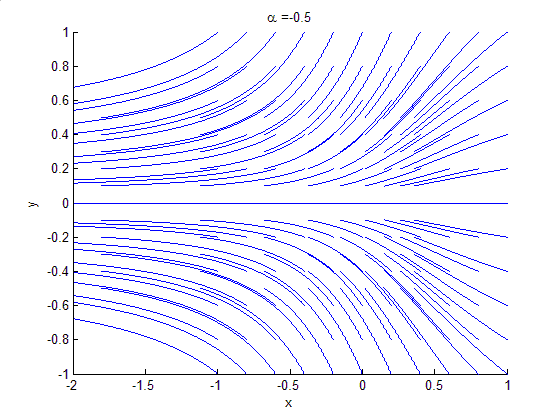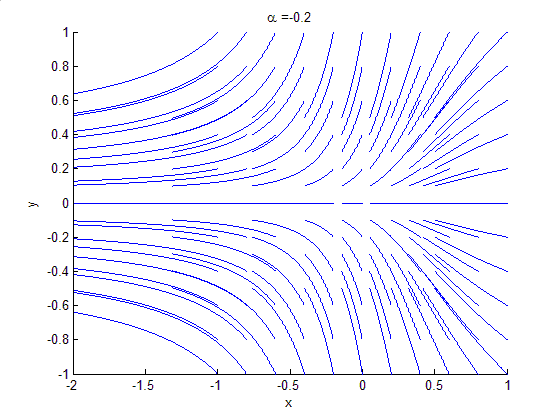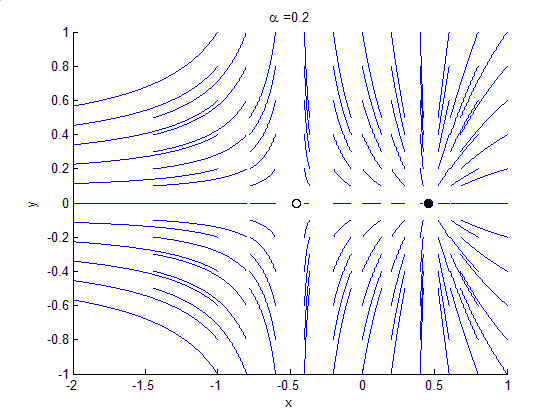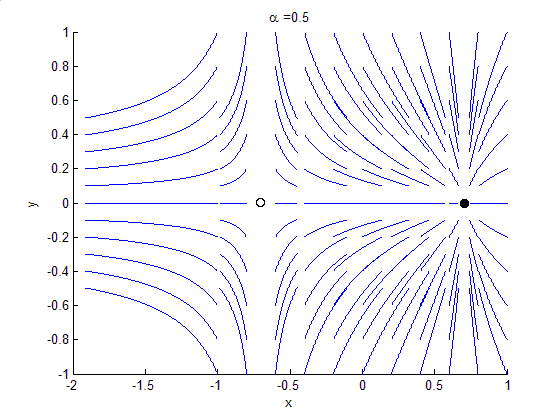
Bifurcation Theory
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems (described by ordinary, delay or partial differential equations) and discrete systems (described by maps). The name "bifurcation" was first introduced by Henri Poincaré in 1885 in the first paper in mathematics showing such a behavior. Henri Poincaré also later named various types of stationary points and classified them . Bifurcation types It is useful to divide bifurcations into two principal classes: * Local bifurcations, which can b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logistic Map Bifurcation Diagram, Matplotlib
Logistic may refer to: Mathematics * Logistic function, a sigmoid function used in many fields ** Logistic map, a recurrence relation that sometimes exhibits chaos ** Logistic regression, a statistical model using the logistic function ** Logit, the inverse of the logistic function ** Logistic distribution, the derivative of the logistic function, a continuous probability distribution, used in probability theory and statistics * Mathematical logic, subfield of mathematics exploring the applications of formal logic to mathematics Other uses * Logistics, the management of resources and their distributions ** Logistic engineering, the scientific study of logistics ** Military logistics Military logistics is the discipline of planning and carrying out the movement, supply, and maintenance of military forces. In its most comprehensive sense, it is those aspects or military operations that deal with: * Design, development, acqui ..., the study of logistics at the service of militar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epidemic Model
Compartmental models are a very general modelling technique. They are often applied to the mathematical modelling of infectious diseases. The population is assigned to compartments with labels – for example, S, I, or R, (Susceptible, Infectious, or Recovered). People may progress between compartments. The order of the labels usually shows the flow patterns between the compartments; for example SEIS means susceptible, exposed, infectious, then susceptible again. The origin of such models is the early 20th century, with important works being that of Ross in 1916, Ross and Hudson in 1917, Kermack and McKendrick in 1927 and Kendall in 1956. The Reed-Frost model was also a significant and widely-overlooked ancestor of modern epidemiological modelling approaches. The models are most often run with ordinary differential equations (which are deterministic), but can also be used with a stochastic (random) framework, which is more realistic but much more complicated to analyze. Models ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theoretical Ecology
Theoretical ecology is the scientific discipline devoted to the study of ecological systems using theoretical methods such as simple conceptual models, mathematical models, computational simulations, and advanced data analysis. Effective models improve understanding of the natural world by revealing how the dynamics of species populations are often based on fundamental biological conditions and processes. Further, the field aims to unify a diverse range of empirical observations by assuming that common, mechanistic processes generate observable phenomena across species and ecological environments. Based on biologically realistic assumptions, theoretical ecologists are able to uncover novel, non-intuitive insights about natural processes. Theoretical results are often verified by empirical and observational studies, revealing the power of theoretical methods in both predicting and understanding the noisy, diverse biological world. The field is broad and includes foundations in appli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Branching Process
In probability theory, a branching process is a type of mathematical object known as a stochastic process, which consists of collections of random variables. The random variables of a stochastic process are indexed by the natural numbers. The original purpose of branching processes was to serve as a mathematical model of a population in which each individual in generation n produces some random number of individuals in generation n+1, according, in the simplest case, to a fixed probability distribution that does not vary from individual to individual. Branching processes are used to model reproduction; for example, the individuals might correspond to bacteria, each of which generates 0, 1, or 2 offspring with some probability in a single time unit. Branching processes can also be used to model other systems with similar dynamics, e.g., the spread of surnames in genealogy or the propagation of neutrons in a nuclear reactor. A central question in the the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |