Chaos theory on:
[Wikipedia]
[Google]
[Amazon]

 Chaos theory is an
Chaos theory is an
 In common usage, "chaos" means "a state of disorder". However, in chaos theory, the term is defined more precisely. Although no universally accepted mathematical definition of chaos exists, a commonly used definition, originally formulated by Robert L. Devaney, says that to classify a dynamical system as chaotic, it must have these properties:
# it must be sensitive to initial conditions,
# it must be topologically transitive,
# it must have dense periodic orbits.
In some cases, the last two properties above have been shown to actually imply sensitivity to initial conditions. In the discrete-time case, this is true for all continuous maps on
In common usage, "chaos" means "a state of disorder". However, in chaos theory, the term is defined more precisely. Although no universally accepted mathematical definition of chaos exists, a commonly used definition, originally formulated by Robert L. Devaney, says that to classify a dynamical system as chaotic, it must have these properties:
# it must be sensitive to initial conditions,
# it must be topologically transitive,
# it must have dense periodic orbits.
In some cases, the last two properties above have been shown to actually imply sensitivity to initial conditions. In the discrete-time case, this is true for all continuous maps on
 Sensitivity to initial conditions means that each point in a chaotic system is arbitrarily closely approximated by other points that have significantly different future paths or trajectories. Thus, an arbitrarily small change or perturbation of the current trajectory may lead to significantly different future behavior.
Sensitivity to initial conditions is popularly known as the " butterfly effect", so-called because of the title of a paper given by Edward Lorenz in 1972 to the
Sensitivity to initial conditions means that each point in a chaotic system is arbitrarily closely approximated by other points that have significantly different future paths or trajectories. Thus, an arbitrarily small change or perturbation of the current trajectory may lead to significantly different future behavior.
Sensitivity to initial conditions is popularly known as the " butterfly effect", so-called because of the title of a paper given by Edward Lorenz in 1972 to the
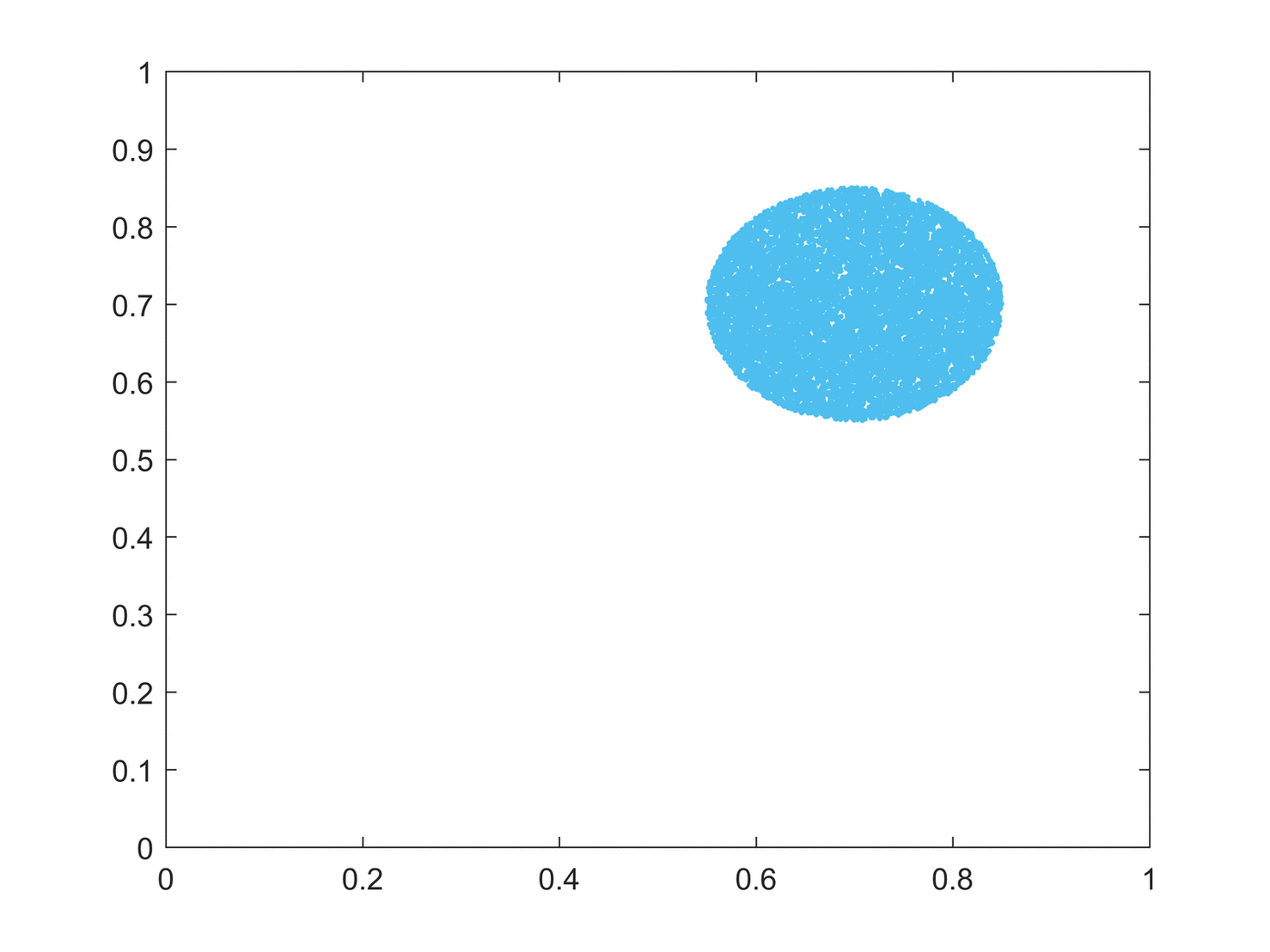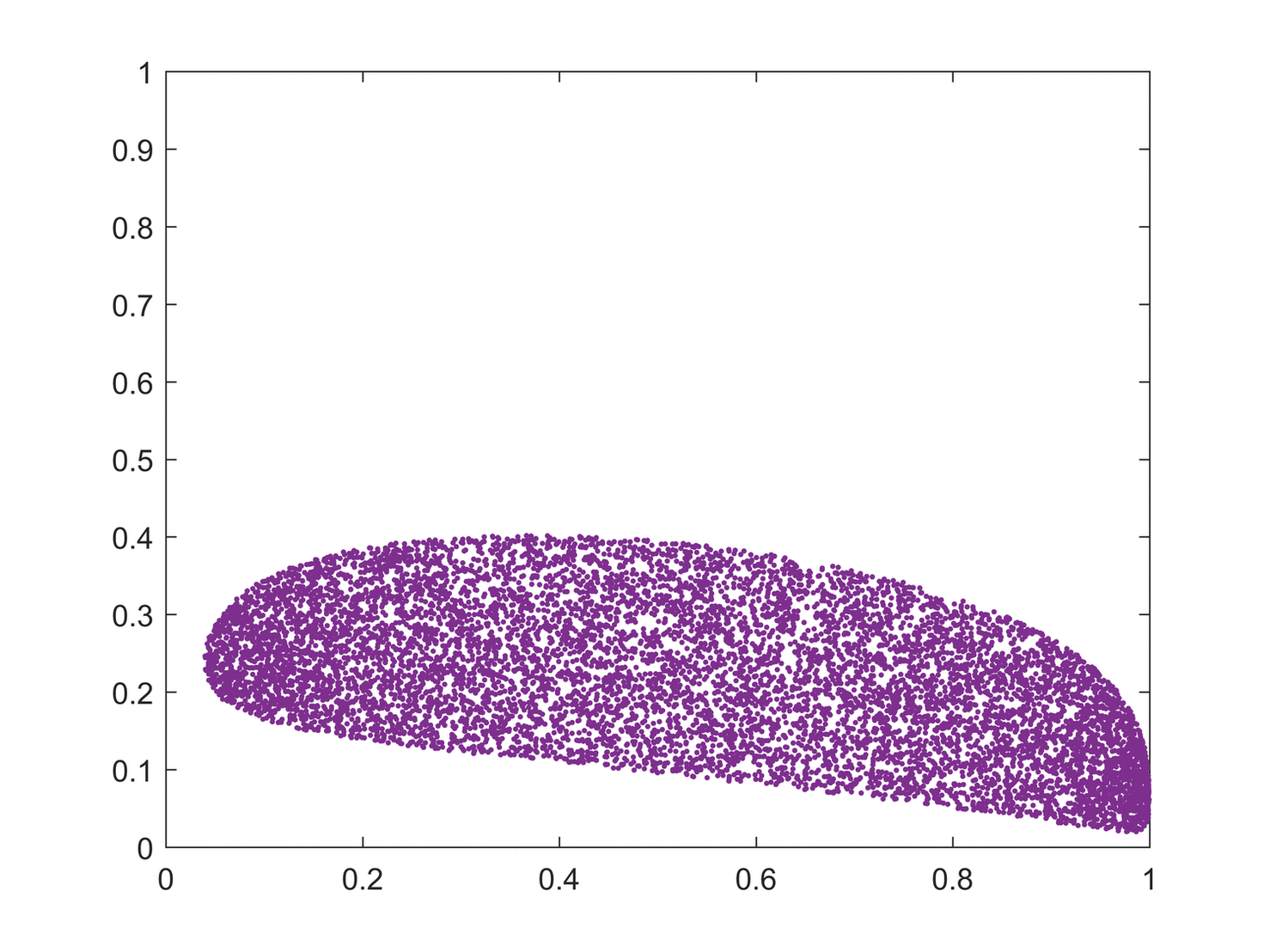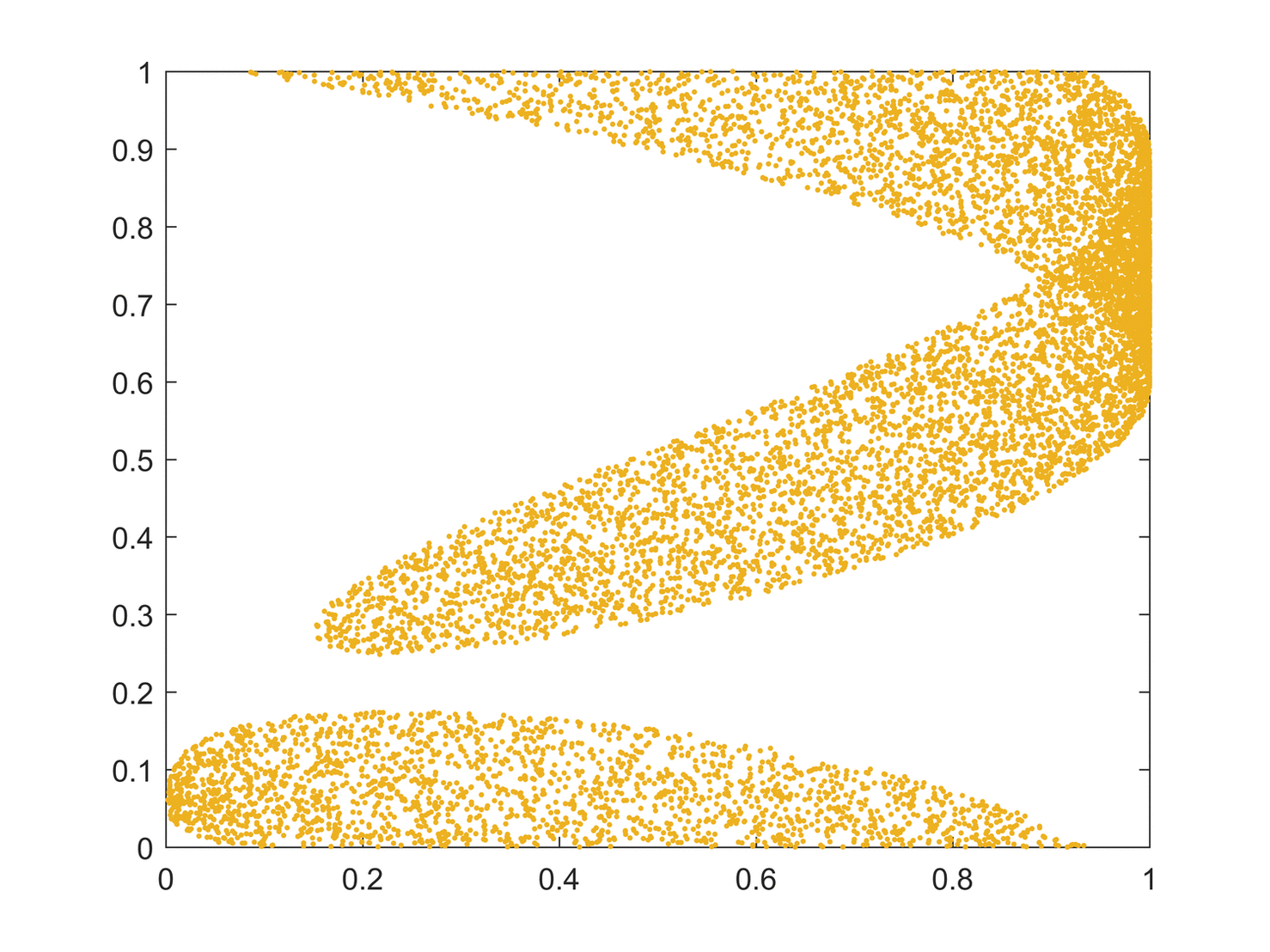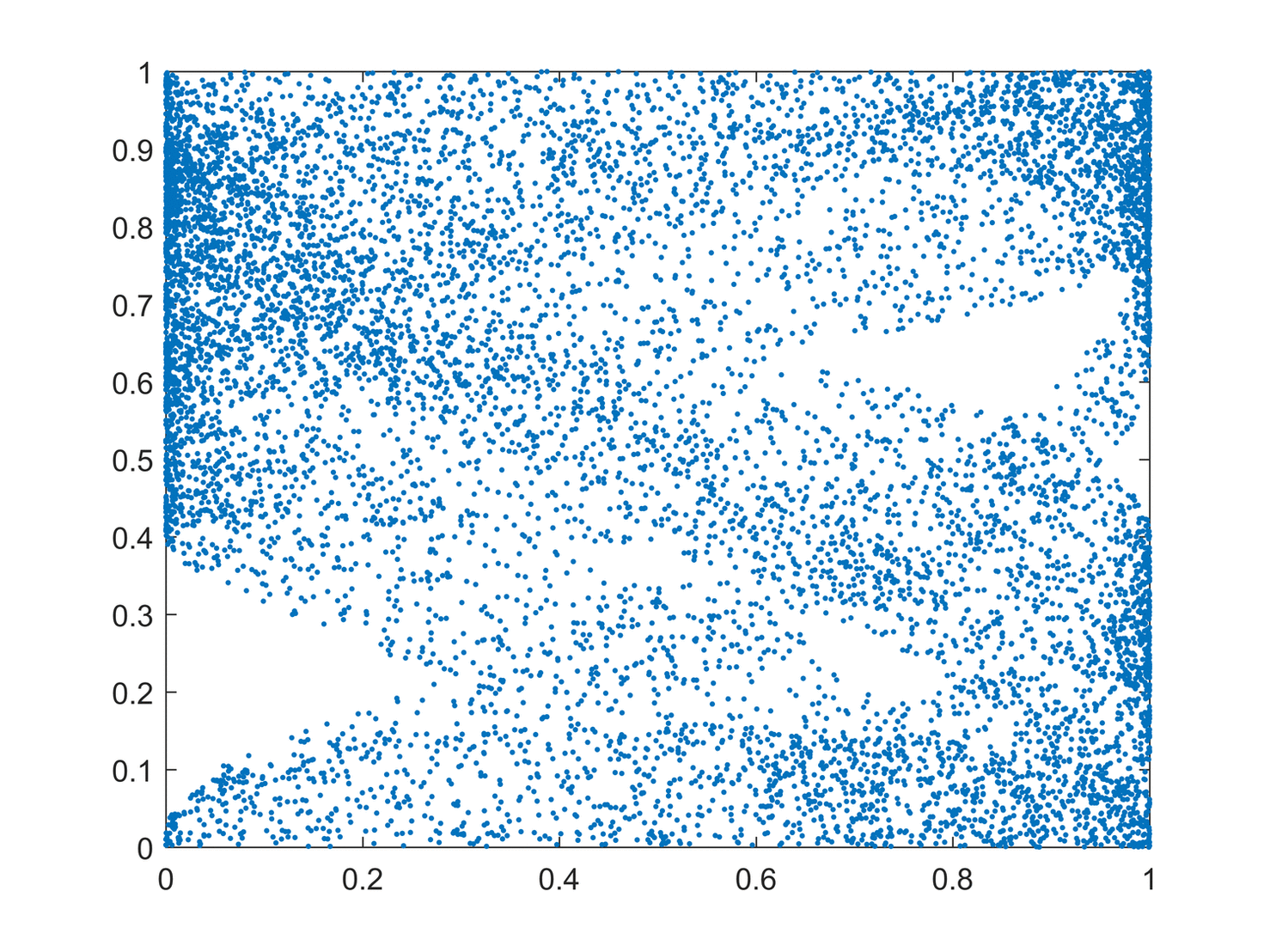
 Some dynamical systems, like the one-dimensional
Some dynamical systems, like the one-dimensional
 In contrast to single type chaotic solutions, recent studies using Lorenz models have emphasized the importance of considering various types of solutions. For example, coexisting chaotic and non-chaotic may appear within the same model (e.g., the double pendulum system) using the same modeling configurations but different initial conditions. The findings of attractor coexistence, obtained from classical and generalized Lorenz models, suggested a revised view that ŌĆ£the entirety of weather possesses a dual nature of chaos and order with distinct predictabilityŌĆØ, in contrast to the conventional view of ŌĆ£weather is chaoticŌĆØ.
In contrast to single type chaotic solutions, recent studies using Lorenz models have emphasized the importance of considering various types of solutions. For example, coexisting chaotic and non-chaotic may appear within the same model (e.g., the double pendulum system) using the same modeling configurations but different initial conditions. The findings of attractor coexistence, obtained from classical and generalized Lorenz models, suggested a revised view that ŌĆ£the entirety of weather possesses a dual nature of chaos and order with distinct predictabilityŌĆØ, in contrast to the conventional view of ŌĆ£weather is chaoticŌĆØ.
 Discrete chaotic systems, such as the
Discrete chaotic systems, such as the
or infinite-dimensional.
The Poincar├®ŌĆōBendixson theorem states that a two-dimensional differential equation has very regular behavior. The Lorenz attractor discussed below is generated by a system of three differential equations such as:
:
where , , and make up the system state, is time, and , , are the system
 Chaos theory is an
Chaos theory is an interdisciplinary
Interdisciplinarity or interdisciplinary studies involves the combination of multiple academic disciplines into one activity (e.g., a research project). It draws knowledge from several other fields like sociology, anthropology, psychology, ec ...
area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws
Law is a set of rules that are created and are enforceable by social or governmental institutions to regulate behavior,Robertson, ''Crimes against humanity'', 90. with its precise definition a matter of longstanding debate. It has been vario ...
of dynamical system
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water i ...
s that are highly sensitive to initial conditions, and were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex system
A complex system is a system composed of many components which may interact with each other. Examples of complex systems are Earth's global climate, organisms, the human brain, infrastructure such as power grid, transportation or communication sy ...
s, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as ill ...
, and self-organization
Self-organization, also called spontaneous order in the social sciences, is a process where some form of overall order arises from local interactions between parts of an initially disordered system. The process can be spontaneous when suffic ...
. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other ...
can result in large differences in a later state (meaning that there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil
Brazil ( pt, Brasil; ), officially the Federative Republic of Brazil (Portuguese: ), is the largest country in both South America and Latin America. At and with over 217 million people, Brazil is the world's fifth-largest country by area ...
can cause a tornado
A tornado is a violently rotating column of air that is in contact with both the surface of the Earth and a cumulonimbus cloud or, in rare cases, the base of a cumulus cloud. It is often referred to as a twister, whirlwind or cyclone, alt ...
in Texas
Texas (, ; Spanish language, Spanish: ''Texas'', ''Tejas'') is a state in the South Central United States, South Central region of the United States. At 268,596 square miles (695,662 km2), and with more than 29.1 million residents in 2 ...
.
Small differences in initial conditions, such as those due to errors in measurements or due to rounding errors in numerical computation, can yield widely diverging outcomes for such dynamical systems, rendering long-term prediction of their behavior impossible in general. This can happen even though these systems are deterministic, meaning that their future behavior follows a unique evolution and is fully determined by their initial conditions, with no random
In common usage, randomness is the apparent or actual lack of pattern or predictability in events. A random sequence of events, symbols or steps often has no order and does not follow an intelligible pattern or combination. Individual rando ...
elements involved. In other words, the deterministic nature of these systems does not make them predictable. This behavior is known as deterministic chaos, or simply chaos. The theory was summarized by Edward Lorenz as:
Chaotic behavior exists in many natural systems, including fluid flow, heartbeat irregularities, weather, and climate. It also occurs spontaneously in some systems with artificial components, such as the road traffic. This behavior can be studied through the analysis of a chaotic mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in the natural sciences (such as physics, ...
, or through analytical techniques such as recurrence plots and Poincar├® map
In mathematics, particularly in dynamical systems, a first recurrence map or Poincar├® map, named after Henri Poincar├®, is the intersection of a periodic orbit in the state space of a continuous dynamical system with a certain lower-dimensional ...
s. Chaos theory has applications in a variety of disciplines, including meteorology
Meteorology is a branch of the atmospheric sciences (which include atmospheric chemistry and physics) with a major focus on weather forecasting. The study of meteorology dates back millennia, though significant progress in meteorology did no ...
, anthropology
Anthropology is the scientific study of humanity, concerned with human behavior, human biology, cultures, societies, and linguistics, in both the present and past, including past human species. Social anthropology studies patterns of be ...
, sociology
Sociology is a social science that focuses on society, human social behavior, patterns of social relationships, social interaction, and aspects of culture associated with everyday life. It uses various methods of empirical investigation and ...
, environmental science
Environmental science is an interdisciplinary academic field that integrates physics, biology, and geography (including ecology, chemistry, plant science, zoology, mineralogy, oceanography, limnology, soil science, geology and physical ...
, computer science
Computer science is the study of computation, automation, and information. Computer science spans theoretical disciplines (such as algorithms, theory of computation, information theory, and automation) to practical disciplines (includin ...
, engineering
Engineering is the use of scientific method, scientific principles to design and build machines, structures, and other items, including bridges, tunnels, roads, vehicles, and buildings. The discipline of engineering encompasses a broad rang ...
, economics
Economics () is the social science that studies the production, distribution, and consumption of goods and services.
Economics focuses on the behaviour and interactions of economic agents and how economies work. Microeconomics analy ...
, ecology
Ecology () is the study of the relationships between living organisms, including humans, and their physical environment. Ecology considers organisms at the individual, population, community, ecosystem, and biosphere level. Ecology overl ...
, and pandemic
A pandemic () is an epidemic of an infectious disease that has spread across a large region, for instance multiple continents or worldwide, affecting a substantial number of individuals. A widespread endemic disease with a stable number of i ...
crisis management
Crisis management is the process by which an organization deals with a disruptive and unexpected event that threatens to harm the organization or its stakeholders. The study of crisis management originated with large-scale industrial and envir ...
. The theory formed the basis for such fields of study as complex dynamical systems, edge of chaos theory, and self-assembly processes.
Introduction
Chaos theory concerns deterministic systems whose behavior can, in principle, be predicted. Chaotic systems are predictable for a while and then 'appear' to become random. The amount of time for which the behavior of a chaotic system can be effectively predicted depends on three things: how much uncertainty can be tolerated in the forecast, how accurately its current state can be measured, and a time scale depending on the dynamics of the system, called the Lyapunov time. Some examples of Lyapunov times are: chaotic electrical circuits, about 1 millisecond; weather systems, a few days (unproven); the inner solar system, 4 to 5 million years. In chaotic systems, the uncertainty in a forecast increases exponentially with elapsed time. Hence, mathematically, doubling the forecast time more than squares the proportional uncertainty in the forecast. This means, in practice, a meaningful prediction cannot be made over an interval of more than two or three times the Lyapunov time. When meaningful predictions cannot be made, the system appears random. Chaos theory is a method of qualitative and quantitative analysis to investigate the behavior of dynamic systems that cannot be explained and predicted by single data relationships, but must be explained and predicted by whole, continuous data relationships.Chaotic dynamics
metric space
In mathematics, a metric space is a set together with a notion of '' distance'' between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are the most general sett ...
s. In these cases, while it is often the most practically significant property, "sensitivity to initial conditions" need not be stated in the definition.
If attention is restricted to intervals, the second property implies the other two. An alternative and a generally weaker definition of chaos uses only the first two properties in the above list.
Sensitivity to initial conditions
 Sensitivity to initial conditions means that each point in a chaotic system is arbitrarily closely approximated by other points that have significantly different future paths or trajectories. Thus, an arbitrarily small change or perturbation of the current trajectory may lead to significantly different future behavior.
Sensitivity to initial conditions is popularly known as the " butterfly effect", so-called because of the title of a paper given by Edward Lorenz in 1972 to the
Sensitivity to initial conditions means that each point in a chaotic system is arbitrarily closely approximated by other points that have significantly different future paths or trajectories. Thus, an arbitrarily small change or perturbation of the current trajectory may lead to significantly different future behavior.
Sensitivity to initial conditions is popularly known as the " butterfly effect", so-called because of the title of a paper given by Edward Lorenz in 1972 to the American Association for the Advancement of Science
The American Association for the Advancement of Science (AAAS) is an American international non-profit organization with the stated goals of promoting cooperation among scientists, defending scientific freedom, encouraging scientific responsi ...
in Washington, D.C., entitled ''Predictability: Does the Flap of a Butterfly's Wings in Brazil set off a Tornado in Texas?''. The flapping wing represents a small change in the initial condition of the system, which causes a chain of events that prevents the predictability of large-scale phenomena. Had the butterfly not flapped its wings, the trajectory of the overall system could have been vastly different.
As suggested in Lorenz's book entitled ''"The Essence of Chaos"'', published in 1993,┬Ā''"sensitive dependence can serve as an acceptable definition of chaos"''. In the same book, Lorenz defined the butterfly effect as: ''"The phenomenon that a small alteration in the state of a dynamical system will cause subsequent states to differ greatly from the states that would have followed without the alteration."''┬ĀThe above definition is consistent with the sensitive dependence of solutions on initial conditions (SDIC). An idealized skiing model was developed to illustrate the sensitivity of time-varying paths to initial positions. A predictability horizon can be determined before the onset of SDIC (i.e., prior to significant separations of initial nearby trajectories).
A consequence of sensitivity to initial conditions is that if we start with a limited amount of information about the system (as is usually the case in practice), then beyond a certain time, the system would no longer be predictable. This is most prevalent in the case of weather, which is generally predictable only about a week ahead. This does not mean that one cannot assert anything about events far in the futureŌĆöonly that some restrictions on the system are present. For example, we know that the temperature of the surface of the earth will not naturally reach or fall below on earth (during the current geologic era), but we cannot predict exactly which day will have the hottest temperature of the year.
In more mathematical terms, the Lyapunov exponent
In mathematics, the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories. Quantitatively, two trajectories in phase space with in ...
measures the sensitivity to initial conditions, in the form of rate of exponential divergence from the perturbed initial conditions. More specifically, given two starting trajectories
A trajectory or flight path is the path that an object with mass in motion follows through space as a function of time. In classical mechanics, a trajectory is defined by Hamiltonian mechanics via canonical coordinates; hence, a complete traj ...
in the phase space
In dynamical system theory, a phase space is a space in which all possible states of a system are represented, with each possible state corresponding to one unique point in the phase space. For mechanical systems, the phase space usual ...
that are infinitesimally close, with initial separation , the two trajectories end up diverging at a rate given by
:
where is the time and is the Lyapunov exponent. The rate of separation depends on the orientation of the initial separation vector, so a whole spectrum of Lyapunov exponents can exist. The number of Lyapunov exponents is equal to the number of dimensions of the phase space, though it is common to just refer to the largest one. For example, the maximal Lyapunov exponent (MLE) is most often used, because it determines the overall predictability of the system. A positive MLE is usually taken as an indication that the system is chaotic.
In addition to the above property, other properties related to sensitivity of initial conditions also exist. These include, for example, measure-theoretical mixing (as discussed in ergodic
In mathematics, ergodicity expresses the idea that a point of a moving system, either a dynamical system or a stochastic process, will eventually visit all parts of the space that the system moves in, in a uniform and random sense. This implies t ...
theory) and properties of a K-system.
Non-periodicity
A chaotic system may have sequences of values for the evolving variable that exactly repeat themselves, giving periodic behavior starting from any point in that sequence. However, such periodic sequences are repelling rather than attracting, meaning that if the evolving variable is outside the sequence, however close, it will not enter the sequence and in fact, will diverge from it. Thus for almost all initial conditions, the variable evolves chaotically with non-periodic behavior.Topological mixing

Topological mixing
In mathematics, mixing is an abstract concept originating from physics: the attempt to describe the irreversible thermodynamic process of mixing in the everyday world: mixing paint, mixing drinks, industrial mixing, ''etc''.
The concept appear ...
(or the weaker condition of topological transitivity) means that the system evolves over time so that any given region or open set
In mathematics, open sets are a generalization of open intervals in the real line.
In a metric space (a set along with a distance defined between any two points), open sets are the sets that, with every point , contain all points that a ...
of its phase space
In dynamical system theory, a phase space is a space in which all possible states of a system are represented, with each possible state corresponding to one unique point in the phase space. For mechanical systems, the phase space usual ...
eventually overlaps with any other given region. This mathematical concept of "mixing" corresponds to the standard intuition, and the mixing of colored dyes or fluids is an example of a chaotic system.
Topological mixing is often omitted from popular accounts of chaos, which equate chaos with only sensitivity to initial conditions. However, sensitive dependence on initial conditions alone does not give chaos. For example, consider the simple dynamical system produced by repeatedly doubling an initial value. This system has sensitive dependence on initial conditions everywhere, since any pair of nearby points eventually becomes widely separated. However, this example has no topological mixing, and therefore has no chaos. Indeed, it has extremely simple behavior: all points except 0 tend to positive or negative infinity.
Topological transitivity
A map is said to be topologically transitive if for any pair of non-emptyopen set
In mathematics, open sets are a generalization of open intervals in the real line.
In a metric space (a set along with a distance defined between any two points), open sets are the sets that, with every point , contain all points that a ...
s , there exists such that . Topological transitivity is a weaker version of topological mixing
In mathematics, mixing is an abstract concept originating from physics: the attempt to describe the irreversible thermodynamic process of mixing in the everyday world: mixing paint, mixing drinks, industrial mixing, ''etc''.
The concept appear ...
. Intuitively, if a map is topologically transitive then given a point ''x'' and a region ''V'', there exists a point ''y'' near ''x'' whose orbit passes through ''V''. This implies that it is impossible to decompose the system into two open sets.
An important related theorem is the Birkhoff Transitivity Theorem. It is easy to see that the existence of a dense orbit implies topological transitivity. The Birkhoff Transitivity Theorem states that if ''X'' is a second countable, complete metric space
In mathematical analysis, a metric space is called complete (or a Cauchy space) if every Cauchy sequence of points in has a limit that is also in .
Intuitively, a space is complete if there are no "points missing" from it (inside or at the bo ...
, then topological transitivity implies the existence of a dense set
In topology and related areas of mathematics, a subset ''A'' of a topological space ''X'' is said to be dense in ''X'' if every point of ''X'' either belongs to ''A'' or else is arbitrarily "close" to a member of ''A'' — for instance, the ...
of points in ''X'' that have dense orbits.
Density of periodic orbits
For a chaotic system to have dense periodic orbits means that every point in the space is approached arbitrarily closely by periodic orbits. The one-dimensionallogistic map
The logistic map is a polynomial mapping (equivalently, recurrence relation) of degree 2, often referred to as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations. The map was popula ...
defined by ''x'' ŌåÆ 4 ''x'' (1 ŌĆō ''x'') is one of the simplest systems with density of periodic orbits. For example, ŌåÆ ŌåÆ (or approximately 0.3454915 ŌåÆ 0.9045085 ŌåÆ 0.3454915) is an (unstable) orbit of period 2, and similar orbits exist for periods 4, 8, 16, etc. (indeed, for all the periods specified by Sharkovskii's theorem).
Sharkovskii's theorem is the basis of the Li and Yorke (1975) proof that any continuous one-dimensional system that exhibits a regular cycle of period three will also display regular cycles of every other length, as well as completely chaotic orbits.
Strange attractors
 Some dynamical systems, like the one-dimensional
Some dynamical systems, like the one-dimensional logistic map
The logistic map is a polynomial mapping (equivalently, recurrence relation) of degree 2, often referred to as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations. The map was popula ...
defined by ''x'' ŌåÆ 4 ''x'' (1 ŌĆō ''x''), are chaotic everywhere, but in many cases chaotic behavior is found only in a subset of phase space. The cases of most interest arise when the chaotic behavior takes place on an attractor
In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain ...
, since then a large set of initial conditions leads to orbits that converge to this chaotic region.
An easy way to visualize a chaotic attractor is to start with a point in the basin of attraction of the attractor, and then simply plot its subsequent orbit. Because of the topological transitivity condition, this is likely to produce a picture of the entire final attractor, and indeed both orbits shown in the figure on the right give a picture of the general shape of the Lorenz attractor. This attractor results from a simple three-dimensional model of the Lorenz
Lorenz is an originally German name derived from the Roman surname Laurentius, which means "from Laurentum".
Given name
People with the given name Lorenz include:
* Prince Lorenz of Belgium (born 1955), member of the Belgian royal family by hi ...
weather system. The Lorenz attractor is perhaps one of the best-known chaotic system diagrams, probably because it is not only one of the first, but it is also one of the most complex, and as such gives rise to a very interesting pattern that, with a little imagination, looks like the wings of a butterfly.
Unlike fixed-point attractors and limit cycle
In mathematics, in the study of dynamical systems with two-dimensional phase space, a limit cycle is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinit ...
s, the attractors that arise from chaotic systems, known as strange attractors, have great detail and complexity. Strange attractors occur in both continuous dynamical systems (such as the Lorenz system) and in some discrete
Discrete may refer to:
*Discrete particle or quantum in physics, for example in quantum theory
*Discrete device, an electronic component with just one circuit element, either passive or active, other than an integrated circuit
*Discrete group, a ...
systems (such as the H├®non map
The H├®non map, sometimes called H├®nonŌĆōPomeau attractor/map, is a discrete-time dynamical system. It is one of the most studied examples of dynamical systems that exhibit chaotic behavior. The H├®non map takes a point (''xn'', ''yn'' ...
). Other discrete dynamical systems have a repelling structure called a Julia set, which forms at the boundary between basins of attraction of fixed points. Julia sets can be thought of as strange repellers. Both strange attractors and Julia sets typically have a fractal
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as il ...
structure, and the fractal dimension can be calculated for them.
Coexisting attractors
 In contrast to single type chaotic solutions, recent studies using Lorenz models have emphasized the importance of considering various types of solutions. For example, coexisting chaotic and non-chaotic may appear within the same model (e.g., the double pendulum system) using the same modeling configurations but different initial conditions. The findings of attractor coexistence, obtained from classical and generalized Lorenz models, suggested a revised view that ŌĆ£the entirety of weather possesses a dual nature of chaos and order with distinct predictabilityŌĆØ, in contrast to the conventional view of ŌĆ£weather is chaoticŌĆØ.
In contrast to single type chaotic solutions, recent studies using Lorenz models have emphasized the importance of considering various types of solutions. For example, coexisting chaotic and non-chaotic may appear within the same model (e.g., the double pendulum system) using the same modeling configurations but different initial conditions. The findings of attractor coexistence, obtained from classical and generalized Lorenz models, suggested a revised view that ŌĆ£the entirety of weather possesses a dual nature of chaos and order with distinct predictabilityŌĆØ, in contrast to the conventional view of ŌĆ£weather is chaoticŌĆØ.
Minimum complexity of a chaotic system
logistic map
The logistic map is a polynomial mapping (equivalently, recurrence relation) of degree 2, often referred to as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations. The map was popula ...
, can exhibit strange attractors whatever their dimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coor ...
ality. Universality of one-dimensional maps with parabolic maxima and Feigenbaum constants , is well visible with map proposed as a toy
model for discrete laser dynamics:
,
where stands for electric field amplitude, is laser gain as bifurcation parameter. The gradual increase of at interval with qualitatively the same , \infty) changes dynamics from regular to chaotic one with qualitatively the same bifurcation diagram as those for logistic map
The logistic map is a polynomial mapping (equivalently, recurrence relation) of degree 2, often referred to as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations. The map was popula ...
.
In contrast, for continuous dynamical systems, the Poincar├®ŌĆōBendixson theorem">continuous function (topology)">continuous dynamical systems, the Finite-dimensional linear system">Poincar├®ŌĆōBendixson theorem shows that a strange attractor can only arise in three or more dimensions. Dimension (vector space)">Finite-dimensional linear systems are never chaotic; for a dynamical system to display chaotic behavior, it must be either nonlinearity">nonlinear
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other ...parameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when ...
s. Five of the terms on the right hand side are linear, while two are quadratic; a total of seven terms. Another well-known chaotic attractor is generated by the R├Čssler equations, which have only one nonlinear term out of seven. Sprott found a three-dimensional system with just five terms, that had only one nonlinear term, which exhibits chaos for certain parameter values. Zhang and Heidel showed that, at least for dissipative and conservative quadratic systems, three-dimensional quadratic systems with only three or four terms on the right-hand side cannot exhibit chaotic behavior. The reason is, simply put, that solutions to such systems are asymptotic
In analytic geometry, an asymptote () of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the ''x'' or ''y'' coordinates tends to infinity. In projective geometry and related contexts, ...
to a two-dimensional surface and therefore solutions are well behaved.
While the Poincar├®ŌĆōBendixson theorem shows that a continuous dynamical system on the Euclidean plane cannot be chaotic, two-dimensional continuous systems with non-Euclidean geometry can exhibit chaotic behavior. Perhaps surprisingly, chaos may occur also in linear systems, provided they are infinite dimensional. A theory of linear chaos is being developed in a branch of mathematical analysis known as functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure (e.g. inner product, norm, topology, etc.) and the linear functions defined ...
.
The above elegant set of three ordinary differential equations has been referred to as the three-dimensional Lorenz model. Since 1963, higher-dimensional Lorenz models have been developed in numerous studies for examining the impact of an increased degree of nonlinearity, as well as its collective effect with heating and dissipations, on solution stability.
Infinite dimensional maps
The straightforward generalization of coupled discrete maps is based upon convolution integral which mediates interaction between spatially distributed maps: , where kernel is propagator derived as Green function of a relevant physical system, might be logistic map alike