Cycloids on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 The
The
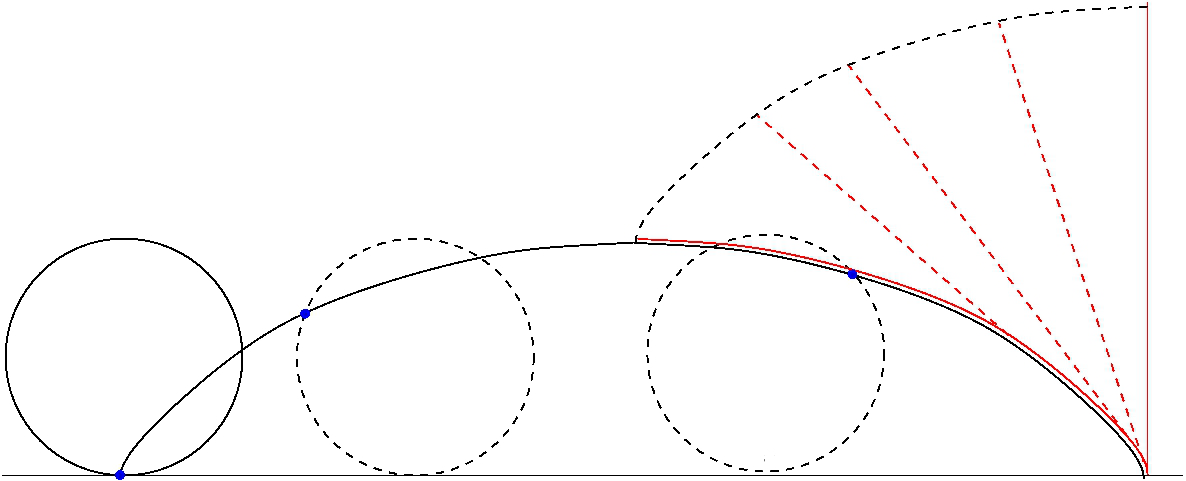
 This demonstration uses the rolling-wheel definition of cycloid, as well as the instantaneous velocity vector of a moving point, tangent to its trajectory. In the adjacent picture, and are two points belonging to two rolling circles, with the base of the first just above the top of the second. Initially, and coincide at the intersection point of the two circles. When the circles roll horizontally with the same speed, and traverse two cycloid curves. Considering the red line connecting and at a given time, one proves ''the line is always'' ''tangent to the lower arc at and orthogonal to the upper arc at ''. Let be the point in common between the upper and lower circles at the given time. Then:
* are colinear: indeed the equal rolling speed gives equal angles , and thus . The point lies on the line therefore and analogously . From the equality of and one has that also . It follows .
*If is the meeting point between the perpendicular from to the line segment and the tangent to the circle at , then the triangle is isosceles, as is easily seen from the construction: and . For the previous noted equality between and then and is isosceles.
*Drawing from the orthogonal segment to , from the straight line tangent to the upper circle, and calling the meeting point, one sees that is a rhombus using the theorems on angles between parallel lines
*Now consider the velocity of . It can be seen as the sum of two components, the rolling velocity and the drifting velocity , which are equal in modulus because the circles roll without skidding. is parallel to , while is tangent to the lower circle at and therefore is parallel to . The rhombus constituted from the components and is therefore similar (same angles) to the rhombus because they have parallel sides. Then , the total velocity of , is parallel to because both are diagonals of two rhombuses with parallel sides and has in common with the contact point . Thus the velocity vector lies on the prolongation of . Because is tangent to the cycloid at , it follows that also coincides with the tangent to the lower cycloid at .
*Analogously, it can be easily demonstrated that is orthogonal to (the other diagonal of the rhombus).
*This proves that the tip of a wire initially stretched on a half arch of the lower cycloid and fixed to the upper circle at will follow the point along its path ''without changing its length'' because the speed of the tip is at each moment orthogonal to the wire (no stretching or compression). The wire will be at the same time tangent at to the lower arc because of the tension and the facts demonstrated above. (If it were not tangent there would be a discontinuity at and consequently unbalanced tension forces.)
This demonstration uses the rolling-wheel definition of cycloid, as well as the instantaneous velocity vector of a moving point, tangent to its trajectory. In the adjacent picture, and are two points belonging to two rolling circles, with the base of the first just above the top of the second. Initially, and coincide at the intersection point of the two circles. When the circles roll horizontally with the same speed, and traverse two cycloid curves. Considering the red line connecting and at a given time, one proves ''the line is always'' ''tangent to the lower arc at and orthogonal to the upper arc at ''. Let be the point in common between the upper and lower circles at the given time. Then:
* are colinear: indeed the equal rolling speed gives equal angles , and thus . The point lies on the line therefore and analogously . From the equality of and one has that also . It follows .
*If is the meeting point between the perpendicular from to the line segment and the tangent to the circle at , then the triangle is isosceles, as is easily seen from the construction: and . For the previous noted equality between and then and is isosceles.
*Drawing from the orthogonal segment to , from the straight line tangent to the upper circle, and calling the meeting point, one sees that is a rhombus using the theorems on angles between parallel lines
*Now consider the velocity of . It can be seen as the sum of two components, the rolling velocity and the drifting velocity , which are equal in modulus because the circles roll without skidding. is parallel to , while is tangent to the lower circle at and therefore is parallel to . The rhombus constituted from the components and is therefore similar (same angles) to the rhombus because they have parallel sides. Then , the total velocity of , is parallel to because both are diagonals of two rhombuses with parallel sides and has in common with the contact point . Thus the velocity vector lies on the prolongation of . Because is tangent to the cycloid at , it follows that also coincides with the tangent to the lower cycloid at .
*Analogously, it can be easily demonstrated that is orthogonal to (the other diagonal of the rhombus).
*This proves that the tip of a wire initially stretched on a half arch of the lower cycloid and fixed to the upper circle at will follow the point along its path ''without changing its length'' because the speed of the tip is at each moment orthogonal to the wire (no stretching or compression). The wire will be at the same time tangent at to the lower arc because of the tension and the facts demonstrated above. (If it were not tangent there would be a discontinuity at and consequently unbalanced tension forces.)
 The
The
 If a simple pendulum is suspended from the cusp of an inverted cycloid, such that the string is constrained to be tangent to one of its arches, and the pendulum's length ''L'' is equal to that of half the arc length of the cycloid (i.e., twice the diameter of the generating circle, ''L = 4r''), the bob of the
If a simple pendulum is suspended from the cusp of an inverted cycloid, such that the string is constrained to be tangent to one of its arches, and the pendulum's length ''L'' is equal to that of half the arc length of the cycloid (i.e., twice the diameter of the generating circle, ''L = 4r''), the bob of the 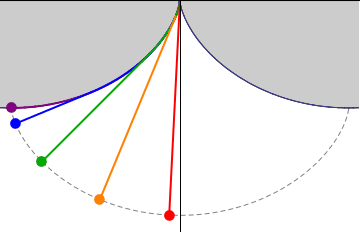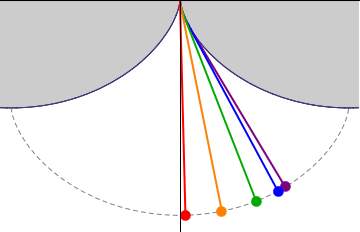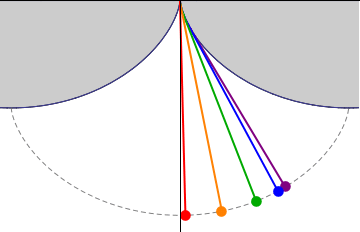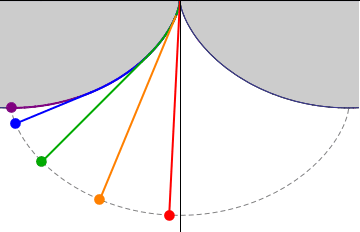 The 17th-century Dutch mathematician
The 17th-century Dutch mathematician
 The cycloidal arch was used by architect
The cycloidal arch was used by architect
link.aps.org
* Edward Kasner & James Newman (1940)
Cycloids
at
A Treatise on The Cycloid and all forms of Cycloidal Curves
monograph by Richard A. Proctor, B.A. posted b
*
Cycloid Curves
' by Sean Madsen with contributions by David von Seggern, Wolfram Demonstrations Project.
Cycloid on PlanetPTC (Mathcad)
by Tom Apostol {{Authority control Roulettes (curve)
 In
In geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, a cycloid is the curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line (geometry), line, but that does not have to be Linearity, straight.
Intuitively, a curve may be thought of as the trace left by a moving point (ge ...
traced by a point on a circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
as it rolls
Roll or Rolls may refer to:
Movement about the longitudinal axis
* Roll angle (or roll rotation), one of the 3 angular degrees of freedom of any stiff body (for example a vehicle), describing motion about the longitudinal axis
** Roll (aviation), ...
along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette
Roulette is a casino game named after the French word meaning ''little wheel'' which was likely developed from the Italian game Biribi''.'' In the game, a player may choose to place a bet on a single number, various groupings of numbers, the ...
, a curve generated by a curve rolling on another curve.
The cycloid, with the cusps pointing upward, is the curve of fastest descent under uniform gravity
In physics, gravity () is a fundamental interaction which causes mutual attraction between all things with mass or energy. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the stro ...
(the brachistochrone curve). It is also the form of a curve for which the period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve).
History
The cycloid has been called "TheHelen
Helen may refer to:
People
* Helen of Troy, in Greek mythology, the most beautiful woman in the world
* Helen (actress) (born 1938), Indian actress
* Helen (given name), a given name (including a list of people with the name)
Places
* Helen, ...
of Geometers" as it caused frequent quarrels among 17th-century mathematicians.
Historians of mathematics have proposed several candidates for the discoverer of the cycloid. Mathematical historian Paul Tannery cited similar work by the Syrian philosopher Iamblichus
Iamblichus (; grc-gre, Ἰάμβλιχος ; Aramaic: 𐡉𐡌𐡋𐡊𐡅 ''Yamlīḵū''; ) was a Syrian neoplatonic philosopher of Arabic origin. He determined a direction later taken by neoplatonism. Iamblichus was also the biographer of ...
as evidence that the curve was known in antiquity. English mathematician John Wallis
John Wallis (; la, Wallisius; ) was an English clergyman and mathematician who is given partial credit for the development of infinitesimal calculus. Between 1643 and 1689 he served as chief cryptographer for Parliament and, later, the royal ...
writing in 1679 attributed the discovery to Nicholas of Cusa
Nicholas of Cusa (1401 – 11 August 1464), also referred to as Nicholas of Kues and Nicolaus Cusanus (), was a German Catholic cardinal, philosopher, theologian, jurist, mathematician, and astronomer. One of the first German proponents of Renai ...
, but subsequent scholarship indicates that either Wallis was mistaken or the evidence he used is now lost. Galileo Galilei
Galileo di Vincenzo Bonaiuti de' Galilei (15 February 1564 – 8 January 1642) was an Italian astronomer, physicist and engineer, sometimes described as a polymath. Commonly referred to as Galileo, his name was pronounced (, ). He was ...
's name was put forward at the end of the 19th century and at least one author reports credit being given to Marin Mersenne
Marin Mersenne, OM (also known as Marinus Mersennus or ''le Père'' Mersenne; ; 8 September 1588 – 1 September 1648) was a French polymath whose works touched a wide variety of fields. He is perhaps best known today among mathematicians for ...
. Beginning with the work of Moritz Cantor and Siegmund Günther
Adam Wilhelm Siegmund Günther (6 February 1848 – 3 February 1923) was a German geographer, mathematician, historian of mathematics and natural scientist.
Early life
Born in 1848 to a German businessman, Günther would go on to attend several G ...
, scholars now assign priority to French mathematician Charles de Bovelles
Charles de Bovelles ( la, Carolus Bovillus; born c. 1475 at Saint-Quentin, died at Ham, Somme after 1566) was a French mathematician and philosopher, and canon of Noyon. His ''Géométrie en françoys'' (1511) was the first scientific work to be ...
based on his description of the cycloid in his ''Introductio in geometriam'', published in 1503. In this work, Bovelles mistakes the arch traced by a rolling wheel as part of a larger circle with a radius 120% larger than the smaller wheel.
Galileo originated the term ''cycloid'' and was the first to make a serious study of the curve. According to his student Evangelista Torricelli
Evangelista Torricelli ( , also , ; 15 October 160825 October 1647) was an Italian physicist and mathematician, and a student of Galileo. He is best known for his invention of the barometer, but is also known for his advances in optics and work o ...
, in 1599 Galileo attempted the quadrature of the cycloid (determining the area under the cycloid) with an unusually empirical approach that involved tracing both the generating circle and the resulting cycloid on sheet metal, cutting them out and weighing them. He discovered the ratio was roughly 3:1, which is the true value, but he incorrectly concluded the ratio was an irrational fraction, which would have made quadrature impossible. Around 1628, Gilles Persone de Roberval likely learned of the quadrature problem from Père Marin Mersenne and effected the quadrature in 1634 by using Cavalieri's Theorem. However, this work was not published until 1693 (in his ''Traité des Indivisibles'').
Constructing the tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More ...
of the cycloid dates to August 1638 when Mersenne received unique methods from Roberval, Pierre de Fermat
Pierre de Fermat (; between 31 October and 6 December 1607 – 12 January 1665) was a French mathematician who is given credit for early developments that led to infinitesimal calculus, including his technique of adequality. In particular, he ...
and René Descartes
René Descartes ( or ; ; Latinized: Renatus Cartesius; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and science. Mathem ...
. Mersenne passed these results along to Galileo, who gave them to his students Torricelli and Viviana, who were able to produce a quadrature. This result and others were published by Torricelli in 1644, which is also the first printed work on the cycloid. This led to Roberval charging Torricelli with plagiarism, with the controversy cut short by Torricelli's early death in 1647.
In 1658, Blaise Pascal had given up mathematics for theology but, while suffering from a toothache, began considering several problems concerning the cycloid. His toothache disappeared, and he took this as a heavenly sign to proceed with his research. Eight days later he had completed his essay and, to publicize the results, proposed a contest. Pascal proposed three questions relating to the center of gravity
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the balance point) is the unique point where the weight function, weighted relative position (vector), position of the distributed mass sums to zero. Thi ...
, area and volume of the cycloid, with the winner or winners to receive prizes of 20 and 40 Spanish doubloon
The doubloon (from Spanish ''doblón'', or "double", i.e. ''double escudo'') was a two-''escudo'' gold coin worth approximately $4 (four Spanish dollars) or 32 '' reales'',
and weighing 6.766 grams (0.218 troy ounce) of 22-karat gold (or 0.917 fi ...
s. Pascal, Roberval and Senator Carcavy were the judges, and neither of the two submissions (by John Wallis
John Wallis (; la, Wallisius; ) was an English clergyman and mathematician who is given partial credit for the development of infinitesimal calculus. Between 1643 and 1689 he served as chief cryptographer for Parliament and, later, the royal ...
and Antoine de Lalouvère
Antoine is a French given name (from the Latin ''Antonius'' meaning 'highly praise-worthy') that is a variant of Danton, Titouan, D'Anton and Antonin.
The name is used in France, Switzerland, Belgium, Canada, West Greenland, Haiti, French Guiana ...
) was judged to be adequate. While the contest was ongoing, Christopher Wren
Sir Christopher Wren PRS FRS (; – ) was one of the most highly acclaimed English architects in history, as well as an anatomist, astronomer, geometer, and mathematician-physicist. He was accorded responsibility for rebuilding 52 churches ...
sent Pascal a proposal for a proof of the rectification
Rectification has the following technical meanings:
Mathematics
* Rectification (geometry), truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points
* Rectifiable curve, in mathematics
* Recti ...
of the cycloid; Roberval claimed promptly that he had known of the proof for years. Wallis published Wren's proof (crediting Wren) in Wallis's ''Tractus Duo'', giving Wren priority for the first published proof.
Fifteen years later, Christiaan Huygens
Christiaan Huygens, Lord of Zeelhem, ( , , ; also spelled Huyghens; la, Hugenius; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor, who is regarded as one of the greatest scientists of ...
had deployed the cycloidal pendulum to improve chronometers and had discovered that a particle would traverse a segment of an inverted cycloidal arch in the same amount of time, regardless of its starting point. In 1686, Gottfried Wilhelm Leibniz
Gottfried Wilhelm (von) Leibniz . ( – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat. He is one of the most prominent figures in both the history of philosophy and the history of mathema ...
used analytic geometry to describe the curve with a single equation. In 1696, Johann Bernoulli posed the brachistochrone problem
In physics and mathematics, a brachistochrone curve (), or curve of fastest descent, is the one lying on the plane between a point ''A'' and a lower point ''B'', where ''B'' is not directly below ''A'', on which a bead slides frictionlessly unde ...
, the solution of which is a cycloid.
Equations
The cycloid through the origin, generated by a circle of radius rolling over the ''-''axis on the positive side (), consists of the points , with where is a realparameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when ...
corresponding to the angle through which the rolling circle has rotated. For given , the circle's centre lies at .
The Cartesian equation
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in t ...
is obtained by solving the '-equation for and substituting into the ''-''equation:or, eliminating the multiple-valued inverse cosine:When is viewed as a function of , the cycloid is differentiable everywhere except at the cusps on the -axis, with the derivative tending toward or near a cusp. The map from to is differentiable, in fact of class ∞, with derivative 0 at the cusps.
The slope of the tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More ...
to the cycloid at the point is given by .
A cycloid segment from one cusp to the next is called an arch of the cycloid, for example the points with and .
Considering the cycloid as the graph of a function , it satisfies the differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, an ...
:
:
Involute
 The
The involute
In mathematics, an involute (also known as an evolvent) is a particular type of curve that is dependent on another shape or curve. An involute of a curve is the locus of a point on a piece of taut string as the string is either unwrapped from or ...
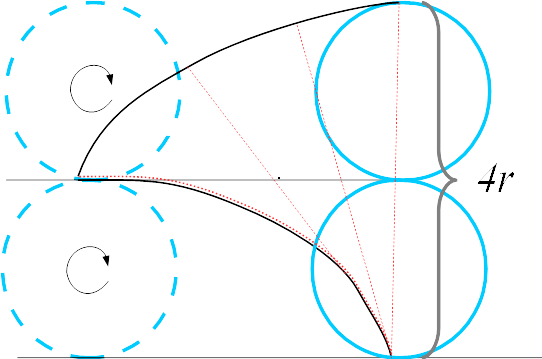
of the cycloid has exactly the same shape as the cycloid it originates from. This can visualized as the path traced by the tip of a wire initially lying on a half arch of the cycloid: as it unrolls while remaining tangent to the original cycloid, it describes a new cycloid (see also cycloidal pendulum
In geometry, a cycloid is the curve traced by a point on a circle as it rolls along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette, a curve generated by a curve rolling on another curv ...
and arc length
ARC may refer to:
Business
* Aircraft Radio Corporation, a major avionics manufacturer from the 1920s to the '50s
* Airlines Reporting Corporation, an airline-owned company that provides ticket distribution, reporting, and settlement services
* ...
).
Demonstration
 This demonstration uses the rolling-wheel definition of cycloid, as well as the instantaneous velocity vector of a moving point, tangent to its trajectory. In the adjacent picture, and are two points belonging to two rolling circles, with the base of the first just above the top of the second. Initially, and coincide at the intersection point of the two circles. When the circles roll horizontally with the same speed, and traverse two cycloid curves. Considering the red line connecting and at a given time, one proves ''the line is always'' ''tangent to the lower arc at and orthogonal to the upper arc at ''. Let be the point in common between the upper and lower circles at the given time. Then:
* are colinear: indeed the equal rolling speed gives equal angles , and thus . The point lies on the line therefore and analogously . From the equality of and one has that also . It follows .
*If is the meeting point between the perpendicular from to the line segment and the tangent to the circle at , then the triangle is isosceles, as is easily seen from the construction: and . For the previous noted equality between and then and is isosceles.
*Drawing from the orthogonal segment to , from the straight line tangent to the upper circle, and calling the meeting point, one sees that is a rhombus using the theorems on angles between parallel lines
*Now consider the velocity of . It can be seen as the sum of two components, the rolling velocity and the drifting velocity , which are equal in modulus because the circles roll without skidding. is parallel to , while is tangent to the lower circle at and therefore is parallel to . The rhombus constituted from the components and is therefore similar (same angles) to the rhombus because they have parallel sides. Then , the total velocity of , is parallel to because both are diagonals of two rhombuses with parallel sides and has in common with the contact point . Thus the velocity vector lies on the prolongation of . Because is tangent to the cycloid at , it follows that also coincides with the tangent to the lower cycloid at .
*Analogously, it can be easily demonstrated that is orthogonal to (the other diagonal of the rhombus).
*This proves that the tip of a wire initially stretched on a half arch of the lower cycloid and fixed to the upper circle at will follow the point along its path ''without changing its length'' because the speed of the tip is at each moment orthogonal to the wire (no stretching or compression). The wire will be at the same time tangent at to the lower arc because of the tension and the facts demonstrated above. (If it were not tangent there would be a discontinuity at and consequently unbalanced tension forces.)
This demonstration uses the rolling-wheel definition of cycloid, as well as the instantaneous velocity vector of a moving point, tangent to its trajectory. In the adjacent picture, and are two points belonging to two rolling circles, with the base of the first just above the top of the second. Initially, and coincide at the intersection point of the two circles. When the circles roll horizontally with the same speed, and traverse two cycloid curves. Considering the red line connecting and at a given time, one proves ''the line is always'' ''tangent to the lower arc at and orthogonal to the upper arc at ''. Let be the point in common between the upper and lower circles at the given time. Then:
* are colinear: indeed the equal rolling speed gives equal angles , and thus . The point lies on the line therefore and analogously . From the equality of and one has that also . It follows .
*If is the meeting point between the perpendicular from to the line segment and the tangent to the circle at , then the triangle is isosceles, as is easily seen from the construction: and . For the previous noted equality between and then and is isosceles.
*Drawing from the orthogonal segment to , from the straight line tangent to the upper circle, and calling the meeting point, one sees that is a rhombus using the theorems on angles between parallel lines
*Now consider the velocity of . It can be seen as the sum of two components, the rolling velocity and the drifting velocity , which are equal in modulus because the circles roll without skidding. is parallel to , while is tangent to the lower circle at and therefore is parallel to . The rhombus constituted from the components and is therefore similar (same angles) to the rhombus because they have parallel sides. Then , the total velocity of , is parallel to because both are diagonals of two rhombuses with parallel sides and has in common with the contact point . Thus the velocity vector lies on the prolongation of . Because is tangent to the cycloid at , it follows that also coincides with the tangent to the lower cycloid at .
*Analogously, it can be easily demonstrated that is orthogonal to (the other diagonal of the rhombus).
*This proves that the tip of a wire initially stretched on a half arch of the lower cycloid and fixed to the upper circle at will follow the point along its path ''without changing its length'' because the speed of the tip is at each moment orthogonal to the wire (no stretching or compression). The wire will be at the same time tangent at to the lower arc because of the tension and the facts demonstrated above. (If it were not tangent there would be a discontinuity at and consequently unbalanced tension forces.)
Area
Using the above parameterization , the area under one arch, is given by: This is three times the area of the rolling circle. This and similar results can be obtained geometrically without calculation by Mamikon'svisual calculus
Visual calculus, invented by Mamikon Mnatsakanian (known as Mamikon), is an approach to solving a variety of integral calculus problems. Many problems that would otherwise seem quite difficult yield to the method with hardly a line of calculatio ...
.
Arc length
 The
The arc length
ARC may refer to:
Business
* Aircraft Radio Corporation, a major avionics manufacturer from the 1920s to the '50s
* Airlines Reporting Corporation, an airline-owned company that provides ticket distribution, reporting, and settlement services
* ...
of one arch is given by
Another geometric way to calculate the length of the cycloid is to notice that when a wire describing an involute
In mathematics, an involute (also known as an evolvent) is a particular type of curve that is dependent on another shape or curve. An involute of a curve is the locus of a point on a piece of taut string as the string is either unwrapped from or ...
has been completely unwrapped from half an arch, it extends itself along two diameters, a length of . This is thus equal to half the length of arch, and that of a complete arch is .
Cycloidal pendulum
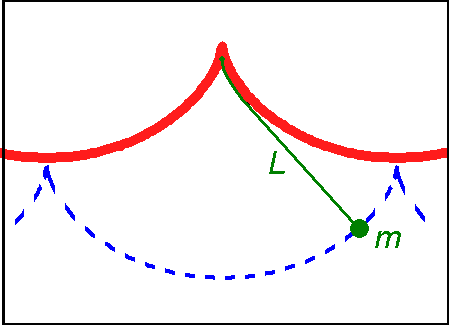
 If a simple pendulum is suspended from the cusp of an inverted cycloid, such that the string is constrained to be tangent to one of its arches, and the pendulum's length ''L'' is equal to that of half the arc length of the cycloid (i.e., twice the diameter of the generating circle, ''L = 4r''), the bob of the
If a simple pendulum is suspended from the cusp of an inverted cycloid, such that the string is constrained to be tangent to one of its arches, and the pendulum's length ''L'' is equal to that of half the arc length of the cycloid (i.e., twice the diameter of the generating circle, ''L = 4r''), the bob of the pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the ...
also traces a cycloid path. Such a pendulum is isochronous, with equal-time swings regardless of amplitude. Introducing a coordinate system centred in the position of the cusp, the equation of motion is given by:
where is the angle that the straight part of the string makes with the vertical axis, and is given by
where is the "amplitude", is the radian frequency of the pendulum and ''g'' the gravitational acceleration.
 The 17th-century Dutch mathematician
The 17th-century Dutch mathematician Christiaan Huygens
Christiaan Huygens, Lord of Zeelhem, ( , , ; also spelled Huyghens; la, Hugenius; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor, who is regarded as one of the greatest scientists of ...
discovered and proved these properties of the cycloid while searching for more accurate pendulum clock designs to be used in navigation.
Related curves
Several curves are related to the cycloid. * Trochoid: generalization of a cycloid in which the point tracing the curve may be inside the rolling circle (curtate) or outside (prolate). * Hypocycloid: variant of a cycloid in which a circle rolls on the inside of another circle instead of a line. *Epicycloid
In geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point on the circumference of a circle—called an ''epicycle''—which rolls without slipping around a fixed circle. It is a particular kind of roulette.
Equati ...
: variant of a cycloid in which a circle rolls on the outside of another circle instead of a line.
* Hypotrochoid
In geometry, a hypotrochoid is a roulette traced by a point attached to a circle of radius rolling around the inside of a fixed circle of radius , where the point is a distance from the center of the interior circle.
The parametric equations f ...
: generalization of a hypocycloid where the generating point may not be on the edge of the rolling circle.
* Epitrochoid: generalization of an epicycloid where the generating point may not be on the edge of the rolling circle.
All these curves are roulettes
The Roulettes are the Royal Australian Air Force's formation aerobatic display team.
They provide about 150 flying displays a year, in Australia and in friendly countries around the Southeast Asian region. The Roulettes form part of the RAAF ...
with a circle rolled along another curve of uniform curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
For curves, the canonic ...
. The cycloid, epicycloids, and hypocycloids have the property that each is similar to its evolute. If ''q'' is the product of that curvature with the circle's radius, signed positive for epi- and negative for hypo-, then the similitude ratio of curve to evolute is 1 + 2''q''.
The classic Spirograph toy traces out hypotrochoid and epitrochoid curves.
Other uses
 The cycloidal arch was used by architect
The cycloidal arch was used by architect Louis Kahn
Louis Isadore Kahn (born Itze-Leib Schmuilowsky; – March 17, 1974) was an Estonian-born American architect based in Philadelphia. After working in various capacities for several firms in Philadelphia, he founded his own atelier in 1935. Whi ...
in his design for the Kimbell Art Museum
The Kimbell Art Museum in Fort Worth, Texas, hosts an art collection as well as traveling art exhibitions, educational programs and an extensive research library. Its initial artwork came from the private collection of Kay and Velma Kimbell, wh ...
in Fort Worth, Texas
Fort Worth is the fifth-largest city in the U.S. state of Texas and the 13th-largest city in the United States. It is the county seat of Tarrant County, covering nearly into four other counties: Denton, Johnson, Parker, and Wise. According ...
. It was also used by Wallace K. Harrison
Wallace Kirkman Harrison (September 28, 1895 – December 2, 1981) was an American architect. Harrison started his professional career with the firm of Corbett, Harrison & MacMurray, participating in the construction of Rockefeller Center. He is ...
in the design of the Hopkins Center
Hopkins Center for the Arts at Dartmouth College is located at 4 East Wheelock Street in Hanover, New Hampshire. The center, which was designed by Wallace Harrison and foreshadows his later design of Manhattan's Lincoln Center, is the college's cu ...
at Dartmouth College
Dartmouth College (; ) is a private research university in Hanover, New Hampshire. Established in 1769 by Eleazar Wheelock, it is one of the nine colonial colleges chartered before the American Revolution. Although founded to educate Native A ...
in Hanover, New Hampshire
Hanover is a town located along the Connecticut River in Grafton County, New Hampshire, United States. As of the 2020 census, its population was 11,870. The town is home to the Ivy League university Dartmouth College, the U.S. Army Corps of Eng ...
.
Early research indicated that some transverse arching curves of the plates of golden age violins are closely modeled by curtate cycloid curves. Later work indicates that curtate cycloids do not serve as general models for these curves, which vary considerably.
See also
*Cyclogon
In geometry, a cyclogon is the curve traced by a vertex of a polygon that rolls without slipping along a straight line. There are no restrictions on the nature of the polygon. It can be a regular polygon like an equilateral triangle or a square. ...
* Cycloid gear
The cycloidal gear profile is a form of toothed gear used in mechanical clocks, rather than the involute gear form used for most other gears. The gear tooth profile is based on the epicycloid and hypocycloid curves, which are the curves generate ...
* List of periodic functions
This is a list of some well-known periodic functions. The constant function , where is independent of , is periodic with any period, but lacks a ''fundamental period''. A definition is given for some of the following functions, though each funct ...
* Tautochrone curve
References
Further reading
* ''An application from physics'': Ghatak, A. & Mahadevan, L. Crack street: the cycloidal wake of acylinder
A cylinder (from ) has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.
A cylinder may also be defined as an infin ...
tearing through a sheet. Physical Review Letters, 91, (2003)link.aps.org
* Edward Kasner & James Newman (1940)
Mathematics and the Imagination
''Mathematics and the Imagination'' is a book published in New York by Simon & Schuster in 1940. The authors are Edward Kasner and James R. Newman. The illustrator Rufus Isaacs (game theorist), Rufus Isaacs provided 169 figures. It rapidly became ...
, pp 196–200, Simon & Schuster
Simon & Schuster () is an American publishing company and a subsidiary of Paramount Global. It was founded in New York City on January 2, 1924 by Richard L. Simon and M. Lincoln Schuster. As of 2016, Simon & Schuster was the third largest publ ...
.
*
External links
* * Retrieved April 27, 2007.Cycloids
at
cut-the-knot
Alexander Bogomolny (January 4, 1948 July 7, 2018) was a Soviet-born Israeli-American mathematician. He was Professor Emeritus of Mathematics at the University of Iowa, and formerly research fellow at the Moscow Institute of Electronics and Math ...
A Treatise on The Cycloid and all forms of Cycloidal Curves
monograph by Richard A. Proctor, B.A. posted b
*
Cycloid Curves
' by Sean Madsen with contributions by David von Seggern, Wolfram Demonstrations Project.
Cycloid on PlanetPTC (Mathcad)
by Tom Apostol {{Authority control Roulettes (curve)