|
Visual Calculus
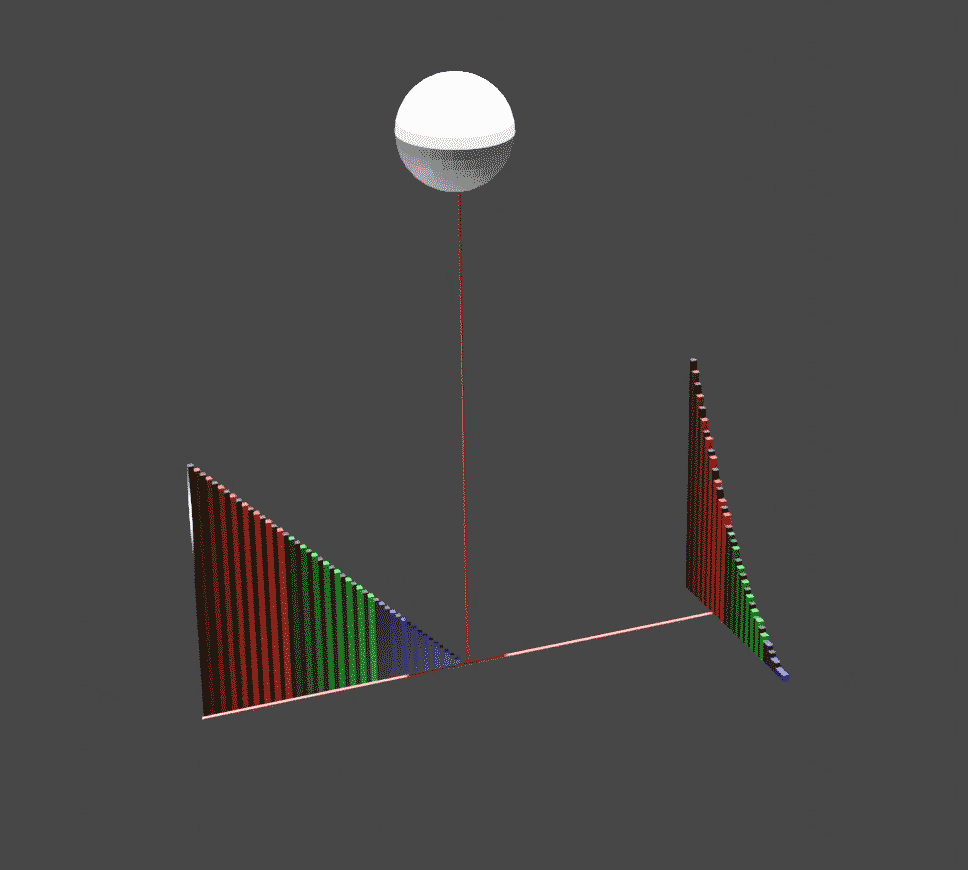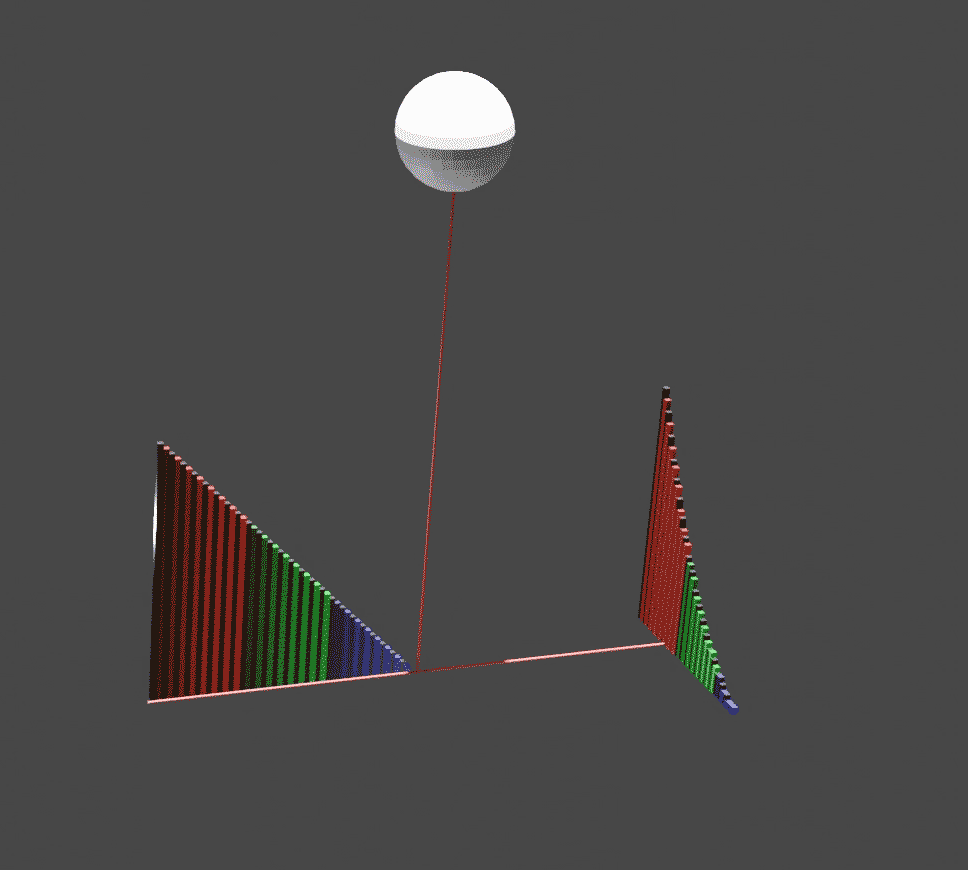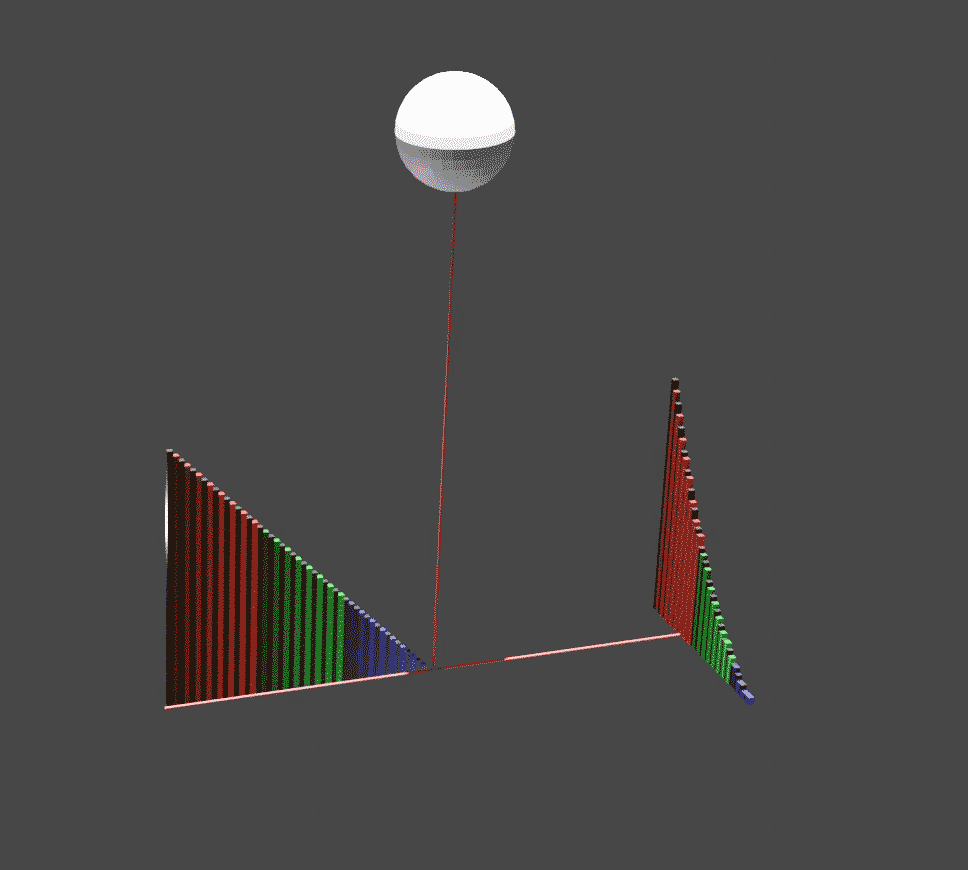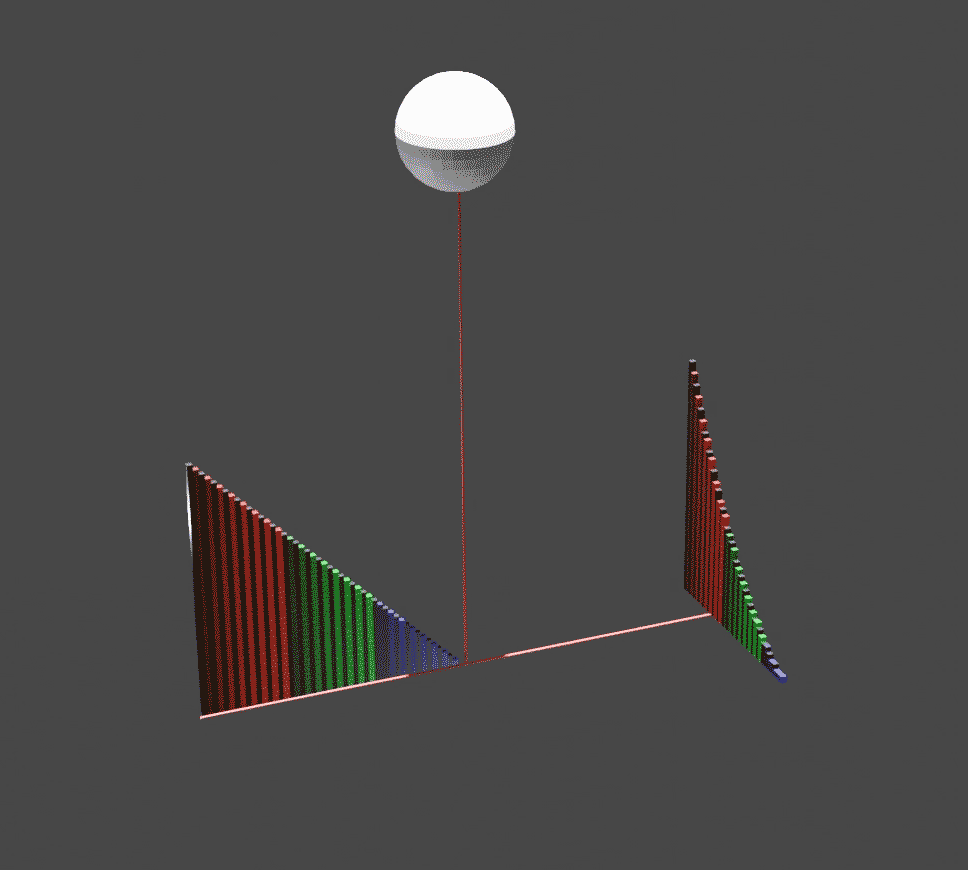
Visual calculus, invented by Mamikon Mnatsakanian (known as Mamikon), is an approach to solving a variety of Integral, integral calculus problems. Many problems that would otherwise seem quite difficult yield to the method with hardly a line of calculation. Mamikon collaborated with Tom Apostol on the 2013 book ''New Horizons in Geometry'' describing the subject. Description Mamikon devised his method in 1959 while an undergraduate, first applying it to a well-known geometry problem: find the area of a ring (annulus (mathematics), annulus), given the length of a Chord (geometry), chord tangent to the inner circumference. Perhaps surprisingly, no additional information is needed; the solution does not depend on the ring's inner and outer dimensions. The traditional approach involves algebra and application of the Pythagorean theorem. Mamikon's method, however, envisions an alternate construction of the ring: first the inner circle alone is drawn, then a constant-length tangent is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cavalieri's Principle
In geometry, Cavalieri's principle, a modern implementation of the method of indivisibles, named after Bonaventura Cavalieri, is as follows: * 2-dimensional case: Suppose two regions in a plane are included between two parallel lines in that plane. If every line parallel to these two lines intersects both regions in line segments of equal length, then the two regions have equal areas. * 3-dimensional case: Suppose two regions in three-space (solids) are included between two parallel planes. If every plane parallel to these two planes intersects both regions in cross section (geometry), cross-sections of equal area, then the two regions have equal volumes. Today Cavalieri's principle is seen as an early step towards integral calculus, and while it is used in some forms, such as its generalization in Fubini's theorem and layer cake representation, results using Cavalieri's principle can often be shown more directly via integration. In the other direction, Cavalieri's principle gre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations. Originally called infinitesimal calculus or "the calculus of infinitesimals", it has two major branches, differential calculus and integral calculus. The former concerns instantaneous Rate of change (mathematics), rates of change, and the slopes of curves, while the latter concerns accumulation of quantities, and areas under or between curves. These two branches are related to each other by the fundamental theorem of calculus. They make use of the fundamental notions of convergence (mathematics), convergence of infinite sequences and Series (mathematics), infinite series to a well-defined limit (mathematics), limit. It is the "mathematical backbone" for dealing with problems where variables change with time or another reference variable. Infinitesimal calculus was formulated separately ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MathWorld
''MathWorld'' is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at Urbana–Champaign. History Eric W. Weisstein, the creator of the site, was a physics and astronomy student who got into the habit of writing notes on his mathematical readings. In 1995 he put his notes online and called it "Eric's Treasure Trove of Mathematics." It contained hundreds of pages/articles, covering a wide range of mathematical topics. The site became popular as an extensive single resource on mathematics on the web. In 1998, he made a contract with CRC Press and the contents of the site were published in print and CD-ROM form, titled ''CRC Concise Encyclopedia of Mathematics''. The free online version became only partially accessible to the public. In 1999 Weisstein we ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Planimeter
A planimeter, also known as a platometer, is a measuring instrument used to determine the area of an arbitrary two-dimensional shape. Construction There are several kinds of planimeters, but all operate in a similar way. The precise way in which they are constructed varies, with the main types of mechanical planimeter being polar, linear, and Prytz or "hatchet" planimeters. The Swiss mathematician Jakob Amsler-Laffon built the first modern planimeter in 1854, the concept having been pioneered by Johann Martin Hermann in 1818. Many developments followed Amsler's famous planimeter, including electronic versions. The Amsler (polar) type consists of a two-bar linkage. At the end of one link is a pointer, used to trace around the boundary of the shape to be measured. The other end of the linkage pivots freely on a weight that keeps it from moving. Near the junction of the two links is a measuring wheel of calibrated diameter, with a scale to show fine rotation, and worm gearing for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pappus's Centroid Theorem
In mathematics, Pappus's centroid theorem (also known as the Guldinus theorem, Pappus–Guldinus theorem or Pappus's theorem) is either of two related theorems dealing with the surface areas and volumes of surfaces and solids of revolution. The theorems are attributed to Pappus of Alexandria and Paul Guldin. Pappus's statement of this theorem appears in print for the first time in 1659, but it was known before, by Kepler in 1615 and by Guldin in 1640. The first theorem The first theorem states that the surface area ''A'' of a surface of revolution generated by rotating a plane curve ''C'' about an axis external to ''C'' and on the same plane is equal to the product of the arc length ''s'' of ''C'' and the distance ''d'' traveled by the geometric centroid of ''C'': A = sd. For example, the surface area of the torus with minor radius ''r'' and major radius ''R'' is A = (2\pi r)(2\pi R) = 4\pi^2 R r. Proof A curve given by the positive function f(x) is bounded by two points ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Method Of Mechanical Theorems
''The Method of Mechanical Theorems'' (), also referred to as ''The Method'', is one of the major surviving works of the ancient Greece, ancient Greek polymath Archimedes. ''The Method'' takes the form of a letter from Archimedes to Eratosthenes, the chief librarian at the Library of Alexandria, and contains the first attested explicit use of method of indivisibles, indivisibles (indivisibles are geometric versions of infinitesimals). The work was originally thought to be lost, but in 1906 was rediscovered in the celebrated Archimedes Palimpsest. The palimpsest includes Archimedes' account of the "mechanical method", so called because it relies on the Center of mass, center of weights of figures (centroid) and the Lever#Law of the lever, law of the lever, which were demonstrated by Archimedes in ''On the Equilibrium of Planes''. Archimedes did not admit the method of indivisibles as part of rigorous mathematics, and therefore did not publish his method in the formal treatises tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hodograph
A hodograph is a diagram that gives a vectorial visual representation of the movement of a body or a fluid. It is the locus of one end of a variable vector, with the other end fixed. The position of any plotted data on such a diagram is proportional to the velocity of the moving particle. It is also called a velocity diagram. It appears to have been used by James Bradley, but its practical development is mainly from Sir William Rowan Hamilton, who published an account of it in the '' Proceedings of the Royal Irish Academy'' in 1846. Applications It is used in physics, astronomy, solid and fluid mechanics to plot deformation of material, motion of planets or any other data that involves the velocities of different parts of a body. Meteorology In meteorology, hodographs are used to plot winds from soundings of the Earth's atmosphere. It is a polar diagram where wind direction is indicated by the angle from the center axis and its strength by the distance from the center. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it Rolling, rolls along a Line (geometry), straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette (curve), roulette, a curve generated by a curve rolling on another curve. The cycloid, with the Cusp (singularity), cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the Frequency, period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). In physics, when a charged particle at rest is put under a uniform Electric field, electric and magnetic field perpendicular to one another, the particle’s trajectory draws out a cycloid. History The cycloid has been called "The Helen of Geometers" as, like Helen of Troy, it caused frequent quarrels among 17th-centur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mamikon Mnatsakanian
Mamikon A. Mnatsakanian (17 April 1942 – 12 April 2021) () was an Armenian physicist. In 1959, he discovered a new proof of the Pythagorean theorem. He received a Ph.D. in physics in 1969 from Yerevan State University, where he became professor of astrophysics. As an undergraduate he specialized in the development of geometric methods for solving calculus problems by a visual approach that makes no use of formulas, which he later developed into his system of visual calculus. He was a Project Associate at Project Mathematics! at the California Institute of Technology. With co-author Tom Apostol, he won the Paul R. Halmos – Lester R. Ford Award given by the Mathematical Association of America for author excellence, in 2005, 2008, and 2010. When Apostol met Mamikon he wrote, "As a teacher of calculus for more than 50 years and as an author of a couple of textbooks on the subject, I was stunned to learn that many standard problems in calculus can be easily solved by an inno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mamikon Cycloid
Mamikon () is an Armenian masculine given name. Notable people with this name include: * Mamikon Gharibyan (born 2004), an Armenian chess grandmaster * Mamikon Mnatsakanian Mamikon A. Mnatsakanian (17 April 1942 – 12 April 2021) () was an Armenian physicist. In 1959, he discovered a new proof of the Pythagorean theorem. He received a Ph.D. in physics in 1969 from Yerevan State University, where he became professor ... (1942 – 2021), an Armenian mathematician {{given name Armenian masculine given names Masculine given names ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |