|
Spirograph
Spirograph is a geometric drawing device that produces mathematical roulette curves of the variety technically known as hypotrochoids and epitrochoids. The well-known toy version was developed by British engineer Denys Fisher and first sold in 1965. The name has been a registered trademark of Hasbro Inc. since 1998 following purchase of the company that had acquired the Denys Fisher company. The Spirograph brand was relaunched worldwide in 2013, with its original product configurations, by Kahootz Toys. History In 1827, Greek-born English architect and engineer Peter Hubert Desvignes developed and advertised a "Speiragraph", a device to create elaborate spiral drawings. A man named J. Jopling soon claimed to have previously invented similar methods. When working in Vienna between 1845 and 1848, Desvignes constructed a version of the machine that would help prevent banknote forgeries, as any of the nearly endless variations of roulette patterns that it could produce were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spirograph2 (cropped)
Spirograph is a geometric drawing device that produces mathematical roulette curves of the variety technically known as hypotrochoids and epitrochoids. The well-known toy version was developed by British engineer Denys Fisher and first sold in 1965. The name has been a registered trademark of Hasbro Inc. since 1998 following purchase of the company that had acquired the Denys Fisher company. The Spirograph brand was relaunched worldwide in 2013, with its original product configurations, by Kahootz Toys. History In 1827, Greek-born English architect and engineer Peter Hubert Desvignes developed and advertised a "Speiragraph", a device to create elaborate spiral drawings. A man named J. Jopling soon claimed to have previously invented similar methods. When working in Vienna between 1845 and 1848, Desvignes constructed a version of the machine that would help prevent banknote forgeries, as any of the nearly endless variations of roulette patterns that it could produce were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kahootz Toys
Kahootz Toys was a toy company based in Ann Arbor, Michigan, best known for the relaunch of the classic toy Spirograph. Kahootz founded in January 2012 by Doug Cass, Colleen Loughman, Joe Yassay, and Brent Oeschger after their previous company, Giddy Up, was sold. Kahootz' initial product offerings were Spirograph and Pomz. In a 2013 interview, Cass stated that they brought back the Spirograph because they saw an opportunity for success in the nostalgia market and felt that it would do well. The first shipment of Spirograph arrived just before Christmas in 2012. The Spirograph (along with Kahootz' Lite-Brite) was exhibited at the 2013 Sweet Suite 13 show in Chicago, Illinois and the 2014 American International Toy Fair in New York City, New York. Since then, Kahootz Toys has expanded and released numerous new products and lines. In 2019 Kahootz launched Y'Art™, a brand of craft kits that allows consumers to color-by-number with yarn. The craft kits were debuted at Toy Fai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Denys Fisher
Denys Fisher (11 May 1918 – 17 September 2002) was an English engineer who invented the spirograph toy and created the company Denys Fisher Toys. He left Leeds University to join the family firmKingfisher (Lubrication) Ltd In 1960 he left the firm to set up his own company, Denys Fisher Engineering, in Leeds. In 1961 the company won a contract with NATO to supply springs and precision components for its 20 mm cannon. Between 1962 and 1964 he developed various drawing machines from Meccano pieces, eventually producing a prototype Spirograph. Patented in 16 countries, it went on sale in Schofields department store in Leeds in 1965. A year later, Fisher licensed Spirograph to Kenner Products in the United States. In 1967 Spirograph was chosen as the UK Toy of the Year. Denys Fisher Toys, which also produced other toys and board games, was sold to Palitoy in 1970 and it was subsequently bought by Hasbro. Through the 1980s and 1990s Fisher continued to work with Hasbro in dev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypocycloid
In geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle. As the radius of the larger circle is increased, the hypocycloid becomes more like the cycloid created by rolling a circle on a line. Properties If the smaller circle has radius , and the larger circle has radius , then the parametric equations for the curve can be given by either: :\begin & x (\theta) = (R - r) \cos \theta + r \cos \left(\frac \theta \right) \\ & y (\theta) = (R - r) \sin \theta - r \sin \left( \frac \theta \right) \end or: :\begin & x (\theta) = r (k - 1) \cos \theta + r \cos \left( (k - 1) \theta \right) \\ & y (\theta) = r (k - 1) \sin \theta - r \sin \left( (k - 1) \theta \right) \end If is an integer, then the curve is closed, and has cusps (i.e., sharp corners, where the curve is not differentiable). Specially for the curve is a straight line and the circles are called Cardano circles. Girolamo Car ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kenner Products
Kenner Products, known simply as Kenner, was an American toy company founded in 1946. Throughout its history, the Kenner brand produced several highly recognizable toys and merchandise lines including action figures like the original series of ''Star Wars'', ''Jurassic Park'' and ''Batman'' as well as die cast models. The company was closed by its corporate parent Hasbro in 2000. History Kenner was founded in 1946 in Cincinnati, Ohio, by brothers Albert, Phillip and Joseph L. Steiner. The company was named after the street where the original corporate offices were located, just north of Cincinnati Union Terminal. It was a pioneer in the use of television advertisement for the marketing of merchandise across the United States, beginning in 1958. In the early 1960s, Kenner introduced its corporate mascot, The Kenner Gooney Bird, which would be used in both its company logo (''"It's Kenner! It's fun!"'') and TV ads, in both animated form and puppetry. One commercial was produce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Guilloché
Guilloché (; or guilloche) is a decorative technique in which a very precise, intricate and repetitive pattern is mechanically engraved into an underlying material via engine turning, which uses a machine of the same name, also called a rose engine lathe. This mechanical technique improved on more time-consuming designs achieved by hand and allowed for greater delicacy, precision, and closeness of line, as well as greater speed. The term ''guilloche'' is also used more generally for repetitive architectural patterns of intersecting or overlapping spirals or other shapes, as used in the Ancient Near East, classical Greece and Rome and neo-classical architecture, and Early Medieval interlace decoration in Anglo-Saxon art and elsewhere. Medieval Cosmatesque stone inlay designs with two ribbons winding around a series of regular central points are very often called guilloche. These central points are often blank, but may contain a figure, such as a rose. These senses are a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
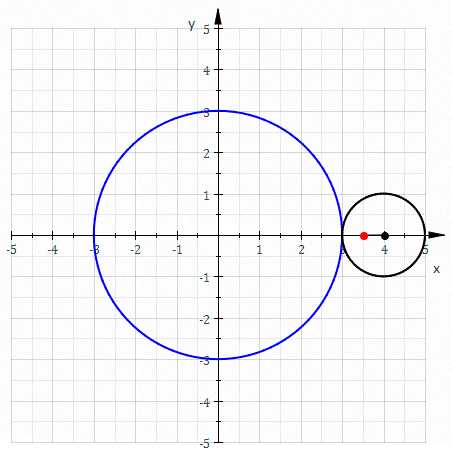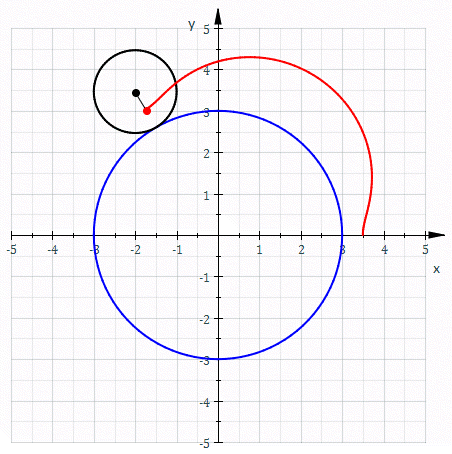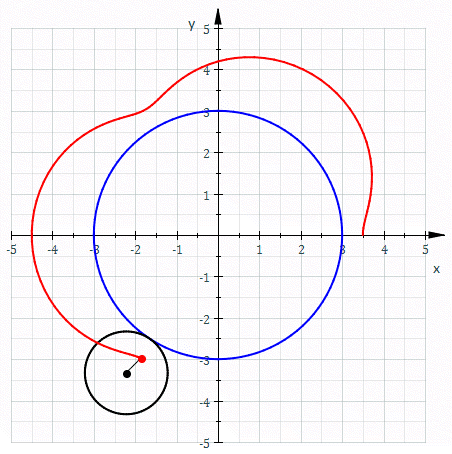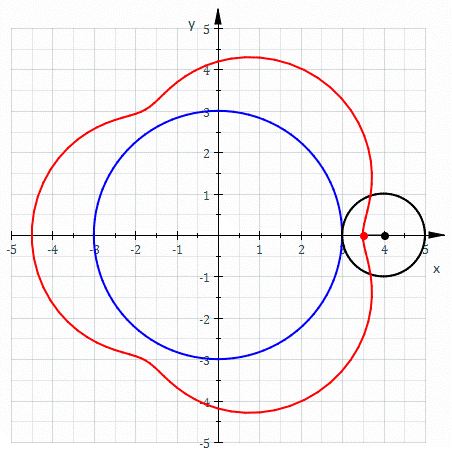
Hypotrochoid
In geometry, a hypotrochoid is a roulette traced by a point attached to a circle of radius rolling around the inside of a fixed circle of radius , where the point is a distance from the center of the interior circle. The parametric equations for a hypotrochoid are: :\begin & x (\theta) = (R - r)\cos\theta + d\cos\left(\theta\right) \\ & y (\theta) = (R - r)\sin\theta - d\sin\left(\theta\right) \end where is the angle formed by the horizontal and the center of the rolling circle (these are not polar equations because is not the polar angle). When measured in radian, takes values from 0 to 2 \pi \times \tfrac (where is least common multiple). Special cases include the hypocycloid with and the ellipse with and . The eccentricity of the ellipse is :e=\frac becoming 1 when d=r (see Tusi couple). The classic Spirograph toy traces out hypotrochoid and epitrochoid curves. Hypotrochoids describe the support of the eigenvalues of some random matrices with cyclic correlatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epitrochoid
In geometry, an epitrochoid ( or ) is a roulette traced by a point attached to a circle of radius rolling around the outside of a fixed circle of radius , where the point is at a distance from the center of the exterior circle. The parametric equations for an epitrochoid are :\begin & x (\theta) = (R + r)\cos\theta - d\cos\left(\theta\right) \\ & y (\theta) = (R + r)\sin\theta - d\sin\left(\theta\right) \end The parameter is geometrically the polar angle of the center of the exterior circle. (However, is not the polar angle of the point (x(\theta),y(\theta)) on the epitrochoid.) Special cases include the limaçon with and the epicycloid with . The classic Spirograph toy traces out epitrochoid and hypotrochoid curves. The orbits of planets in the once popular geocentric Ptolemaic system are epitrochoids (see deferent and epicycle). The orbit of the moon, when centered around the sun, approximates an epitrochoid. The combustion chamber of the Wankel engine is an epitro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Lathe
A geometric lathe was used for making ornamental patterns on the plates used in printing bank notes and postage stamps. It is sometimes called a guilloché lathe. It was developed early in the nineteenth century when efforts were introduced to combat forgery, and is an adaptation of an ornamental turning lathe. The lathe was able to generate intersecting and interlacing patterns of fine lines in various shapes, which were almost impossible to forge by hand-engraving. They were used by many national mints. Further reading *Peter Bower, 'Economic warfare: Banknote Forgery as a deliberate weapon', and Maureen Greenland, 'Compound plate printing and nineteenth-century bank notes, in Virginia Hewitt, ed. ''The Banker's Art: Studies in paper money'', pp 46–63, and pp 84–87, The British Museum Press, 1995, () See also * Security printing * Spirograph * Tusi couple * Guilloché Guilloché (; or guilloche) is a decorative technique in which a very precise, intricate and re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyclograph
A cyclograph (also known as an arcograph) is an instrument for drawing arcs of large diameter circles whose centres are inconveniently or inaccessibly located, one version of which was invented by Scottish architect and mathematician Peter Nicholson. Description In his autobiography, published in 1904, polymath Herbert Spencer eloquently describes his own near re-invention of Nicholson's cyclograph while working as a civil engineer for the Birmingham and Gloucester Railway. See also * Spirograph Spirograph is a geometric drawing device that produces mathematical roulette curves of the variety technically known as hypotrochoids and epitrochoids. The well-known toy version was developed by British engineer Denys Fisher and first sold in ... References {{reflist, colwidth=30em Technical drawing tools ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apsidal Precession
In celestial mechanics, apsidal precession (or apsidal advance) is the precession (gradual rotation) of the line connecting the apsides (line of apsides) of an astronomical body's orbit. The apsides are the orbital points closest (periapsis) and farthest (apoapsis) from its primary body. The apsidal precession is the first time derivative of the argument of periapsis, one of the six main orbital elements of an orbit. Apsidal precession is considered positive when the orbit's axis rotates in the same direction as the orbital motion. An apsidal period is the time interval required for an orbit to precess through 360°. History The ancient Greek astronomer Hipparchus noted the apsidal precession of the Moon's orbit (as the revolution of the Moon's apogee with a period of approximately 8.85 years); it is corrected for in the Antikythera Mechanism (circa 80 BCE) (with the supposed value of 8.88 years per full cycle, correct to within 0.34% of current measurements). The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |