Cycloid Osculating Circle Evolute 2 on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 The
The
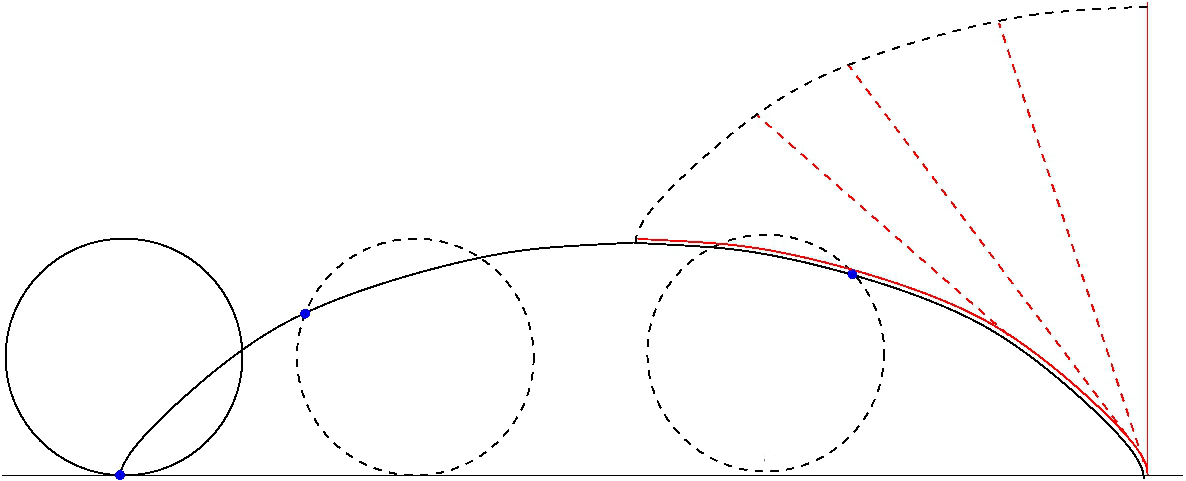
 This demonstration uses the rolling-wheel definition of cycloid, as well as the instantaneous velocity vector of a moving point, tangent to its trajectory. In the adjacent picture, and are two points belonging to two rolling circles, with the base of the first just above the top of the second. Initially, and coincide at the intersection point of the two circles. When the circles roll horizontally with the same speed, and traverse two cycloid curves. Considering the red line connecting and at a given time, one proves ''the line is always'' ''tangent to the lower arc at and orthogonal to the upper arc at ''. Let be the point in common between the upper and lower circles at the given time. Then:
* are colinear: indeed the equal rolling speed gives equal angles , and thus . The point lies on the line therefore and analogously . From the equality of and one has that also . It follows .
*If is the meeting point between the perpendicular from to the line segment and the tangent to the circle at , then the triangle is isosceles, as is easily seen from the construction: and . For the previous noted equality between and then and is isosceles.
*Drawing from the orthogonal segment to , from the straight line tangent to the upper circle, and calling the meeting point, one sees that is a
This demonstration uses the rolling-wheel definition of cycloid, as well as the instantaneous velocity vector of a moving point, tangent to its trajectory. In the adjacent picture, and are two points belonging to two rolling circles, with the base of the first just above the top of the second. Initially, and coincide at the intersection point of the two circles. When the circles roll horizontally with the same speed, and traverse two cycloid curves. Considering the red line connecting and at a given time, one proves ''the line is always'' ''tangent to the lower arc at and orthogonal to the upper arc at ''. Let be the point in common between the upper and lower circles at the given time. Then:
* are colinear: indeed the equal rolling speed gives equal angles , and thus . The point lies on the line therefore and analogously . From the equality of and one has that also . It follows .
*If is the meeting point between the perpendicular from to the line segment and the tangent to the circle at , then the triangle is isosceles, as is easily seen from the construction: and . For the previous noted equality between and then and is isosceles.
*Drawing from the orthogonal segment to , from the straight line tangent to the upper circle, and calling the meeting point, one sees that is a
 The
The
 If a simple pendulum is suspended from the cusp of an inverted cycloid, such that the string is constrained to be tangent to one of its arches, and the pendulum's length ''L'' is equal to that of half the arc length of the cycloid (i.e., twice the diameter of the generating circle, ''L = 4r''), the bob of the
If a simple pendulum is suspended from the cusp of an inverted cycloid, such that the string is constrained to be tangent to one of its arches, and the pendulum's length ''L'' is equal to that of half the arc length of the cycloid (i.e., twice the diameter of the generating circle, ''L = 4r''), the bob of the 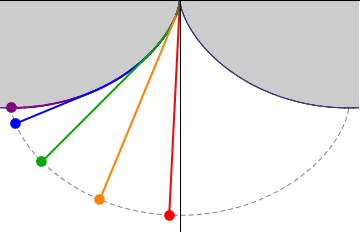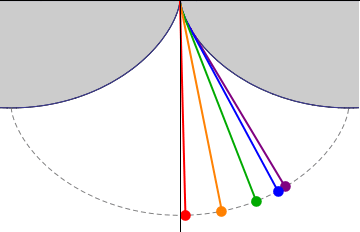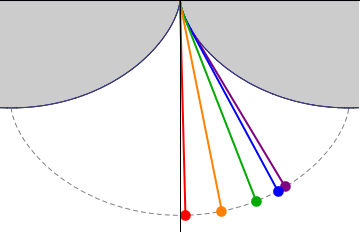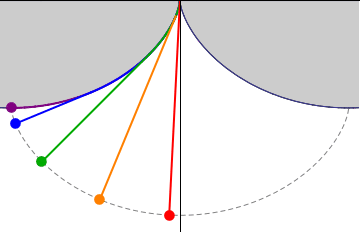 The 17th-century Dutch mathematician
The 17th-century Dutch mathematician
 The cycloidal arch was used by architect
The cycloidal arch was used by architect
link.aps.org
* Edward Kasner & James Newman (1940) Mathematics and the Imagination, pp 196–200,
Cycloids
at cut-the-knot
A Treatise on The Cycloid and all forms of Cycloidal Curves
monograph by Richard A. Proctor, B.A. posted b
*
Cycloid Curves
' by Sean Madsen with contributions by David von Seggern,
Cycloid on PlanetPTC (Mathcad)
by Tom Apostol {{Authority control Roulettes (curve)
 In
In geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, a cycloid is the curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
traced by a point on a circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
as it rolls along a straight line
In geometry, a line is an infinitely long object with no width, depth, or curvature. Thus, lines are one-dimensional objects, though they may exist in two, three, or higher dimension spaces. The word ''line'' may also refer to a line segment ...
without slipping. A cycloid is a specific form of trochoid
In geometry, a trochoid () is a roulette curve formed by a circle rolling along a line. It is the curve traced out by a point fixed to a circle (where the point may be on, inside, or outside the circle) as it rolls along a straight line. If the ...
and is an example of a roulette
Roulette is a casino game named after the French word meaning ''little wheel'' which was likely developed from the Italian game Biribi''.'' In the game, a player may choose to place a bet on a single number, various groupings of numbers, the ...
, a curve generated by a curve rolling on another curve.
The cycloid, with the cusps pointing upward, is the curve of fastest descent under uniform gravity
In physics, gravity () is a fundamental interaction which causes mutual attraction between all things with mass or energy. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the str ...
(the brachistochrone curve
In physics and mathematics, a brachistochrone curve (), or curve of fastest descent, is the one lying on the plane between a point ''A'' and a lower point ''B'', where ''B'' is not directly below ''A'', on which a bead slides frictionlessly unde ...
). It is also the form of a curve for which the period of an object in simple harmonic motion
In mechanics and physics, simple harmonic motion (sometimes abbreviated ) is a special type of periodic motion of a body resulting from a dynamic equilibrium between an inertial force, proportional to the acceleration of the body away from the ...
(rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve
A tautochrone or isochrone curve (from Greek prefixes tauto- meaning ''same'' or iso- ''equal'', and chrono ''time'') is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independ ...
).
History
The cycloid has been called "The Helen of Geometers" as it caused frequent quarrels among 17th-century mathematicians. Historians of mathematics have proposed several candidates for the discoverer of the cycloid. Mathematical historianPaul Tannery
Paul Tannery (20 December 1843 – 27 November 1904) was a French mathematician and historian of mathematics. He was the older brother of mathematician Jules Tannery, to whose ''Notions Mathématiques'' he contributed an historical chapter. Tho ...
cited similar work by the Syrian philosopher Iamblichus as evidence that the curve was known in antiquity. English mathematician John Wallis
John Wallis (; la, Wallisius; ) was an English clergyman and mathematician who is given partial credit for the development of infinitesimal calculus. Between 1643 and 1689 he served as chief cryptographer for Parliament and, later, the roya ...
writing in 1679 attributed the discovery to Nicholas of Cusa
Nicholas of Cusa (1401 – 11 August 1464), also referred to as Nicholas of Kues and Nicolaus Cusanus (), was a German Catholic cardinal, philosopher, theologian, jurist, mathematician, and astronomer. One of the first German proponents of Ren ...
, but subsequent scholarship indicates that either Wallis was mistaken or the evidence he used is now lost. Galileo Galilei
Galileo di Vincenzo Bonaiuti de' Galilei (15 February 1564 – 8 January 1642) was an Italian astronomer, physicist and engineer, sometimes described as a polymath. Commonly referred to as Galileo, his name was pronounced (, ). He w ...
's name was put forward at the end of the 19th century and at least one author reports credit being given to Marin Mersenne
Marin Mersenne, OM (also known as Marinus Mersennus or ''le Père'' Mersenne; ; 8 September 1588 – 1 September 1648) was a French polymath whose works touched a wide variety of fields. He is perhaps best known today among mathematicians for ...
. Beginning with the work of Moritz Cantor
Moritz Benedikt Cantor (23 August 1829 – 10 April 1920) was a German historian of mathematics.
Biography
Cantor was born at Mannheim. He came from a Sephardi Jewish family that had emigrated to the Netherlands from Portugal, another branch of ...
and Siegmund Günther, scholars now assign priority to French mathematician Charles de Bovelles based on his description of the cycloid in his ''Introductio in geometriam'', published in 1503. In this work, Bovelles mistakes the arch traced by a rolling wheel as part of a larger circle with a radius 120% larger than the smaller wheel.
Galileo originated the term ''cycloid'' and was the first to make a serious study of the curve. According to his student Evangelista Torricelli
Evangelista Torricelli ( , also , ; 15 October 160825 October 1647) was an Italian physicist and mathematician, and a student of Galileo. He is best known for his invention of the barometer, but is also known for his advances in optics and work ...
, in 1599 Galileo attempted the quadrature of the cycloid (determining the area under the cycloid) with an unusually empirical approach that involved tracing both the generating circle and the resulting cycloid on sheet metal, cutting them out and weighing them. He discovered the ratio was roughly 3:1, which is the true value, but he incorrectly concluded the ratio was an irrational fraction, which would have made quadrature impossible. Around 1628, Gilles Persone de Roberval likely learned of the quadrature problem from Père Marin Mersenne and effected the quadrature in 1634 by using Cavalieri's Theorem. However, this work was not published until 1693 (in his ''Traité des Indivisibles'').
Constructing the tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. Mo ...
of the cycloid dates to August 1638 when Mersenne received unique methods from Roberval, Pierre de Fermat
Pierre de Fermat (; between 31 October and 6 December 1607 – 12 January 1665) was a French mathematician who is given credit for early developments that led to infinitesimal calculus, including his technique of adequality. In particular, he ...
and René Descartes
René Descartes ( or ; ; Latinized: Renatus Cartesius; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and science. Mathe ...
. Mersenne passed these results along to Galileo, who gave them to his students Torricelli and Viviana, who were able to produce a quadrature. This result and others were published by Torricelli in 1644, which is also the first printed work on the cycloid. This led to Roberval charging Torricelli with plagiarism, with the controversy cut short by Torricelli's early death in 1647.
In 1658, Blaise Pascal had given up mathematics for theology but, while suffering from a toothache, began considering several problems concerning the cycloid. His toothache disappeared, and he took this as a heavenly sign to proceed with his research. Eight days later he had completed his essay and, to publicize the results, proposed a contest. Pascal proposed three questions relating to the center of gravity
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the balance point) is the unique point where the weighted relative position of the distributed mass sums to zero. This is the point to which a force may ...
, area and volume of the cycloid, with the winner or winners to receive prizes of 20 and 40 Spanish doubloon
The doubloon (from Spanish ''doblón'', or "double", i.e. ''double escudo'') was a two-'' escudo'' gold coin worth approximately $4 (four Spanish dollars) or 32 '' reales'',
and weighing 6.766 grams (0.218 troy ounce) of 22- karat gold (or 0.91 ...
s. Pascal, Roberval and Senator Carcavy were the judges, and neither of the two submissions (by John Wallis
John Wallis (; la, Wallisius; ) was an English clergyman and mathematician who is given partial credit for the development of infinitesimal calculus. Between 1643 and 1689 he served as chief cryptographer for Parliament and, later, the roya ...
and Antoine de Lalouvère) was judged to be adequate. While the contest was ongoing, Christopher Wren
Sir Christopher Wren PRS FRS (; – ) was one of the most highly acclaimed English architects in history, as well as an anatomist, astronomer, geometer, and mathematician-physicist. He was accorded responsibility for rebuilding 52 churc ...
sent Pascal a proposal for a proof of the rectification of the cycloid; Roberval claimed promptly that he had known of the proof for years. Wallis published Wren's proof (crediting Wren) in Wallis's ''Tractus Duo'', giving Wren priority for the first published proof.
Fifteen years later, Christiaan Huygens
Christiaan Huygens, Lord of Zeelhem, ( , , ; also spelled Huyghens; la, Hugenius; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor, who is regarded as one of the greatest scientists ...
had deployed the cycloidal pendulum to improve chronometers and had discovered that a particle would traverse a segment of an inverted cycloidal arch in the same amount of time, regardless of its starting point. In 1686, Gottfried Wilhelm Leibniz
Gottfried Wilhelm (von) Leibniz . ( – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat. He is one of the most prominent figures in both the history of philosophy and the history of mat ...
used analytic geometry to describe the curve with a single equation. In 1696, Johann Bernoulli
Johann Bernoulli (also known as Jean or John; – 1 January 1748) was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family. He is known for his contributions to infinitesimal calculus and educating ...
posed the brachistochrone problem, the solution of which is a cycloid.
Equations
The cycloid through the origin, generated by a circle of radius rolling over the ''-''axis on the positive side (), consists of the points , with where is a realparameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when ...
corresponding to the angle through which the rolling circle has rotated. For given , the circle's centre lies at .
The Cartesian equation is obtained by solving the '-equation for and substituting into the ''-''equation:or, eliminating the multiple-valued inverse cosine:When is viewed as a function of , the cycloid is differentiable everywhere except at the cusps on the -axis, with the derivative tending toward or near a cusp. The map from to is differentiable, in fact of class ∞, with derivative 0 at the cusps.
The slope of the tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. Mo ...
to the cycloid at the point is given by .
A cycloid segment from one cusp to the next is called an arch of the cycloid, for example the points with and .
Considering the cycloid as the graph of a function , it satisfies the differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, a ...
:
:
Involute
 The
The involute
In mathematics, an involute (also known as an evolvent) is a particular type of curve that is dependent on another shape or curve. An involute of a curve is the locus of a point on a piece of taut string as the string is either unwrapped from o ...
of the cycloid has exactly the same shape as the cycloid it originates from. This can visualized as the path traced by the tip of a wire initially lying on a half arch of the cycloid: as it unrolls while remaining tangent to the original cycloid, it describes a new cycloid (see also cycloidal pendulum and arc length
ARC may refer to:
Business
* Aircraft Radio Corporation, a major avionics manufacturer from the 1920s to the '50s
* Airlines Reporting Corporation, an airline-owned company that provides ticket distribution, reporting, and settlement services
...
).
Demonstration
 This demonstration uses the rolling-wheel definition of cycloid, as well as the instantaneous velocity vector of a moving point, tangent to its trajectory. In the adjacent picture, and are two points belonging to two rolling circles, with the base of the first just above the top of the second. Initially, and coincide at the intersection point of the two circles. When the circles roll horizontally with the same speed, and traverse two cycloid curves. Considering the red line connecting and at a given time, one proves ''the line is always'' ''tangent to the lower arc at and orthogonal to the upper arc at ''. Let be the point in common between the upper and lower circles at the given time. Then:
* are colinear: indeed the equal rolling speed gives equal angles , and thus . The point lies on the line therefore and analogously . From the equality of and one has that also . It follows .
*If is the meeting point between the perpendicular from to the line segment and the tangent to the circle at , then the triangle is isosceles, as is easily seen from the construction: and . For the previous noted equality between and then and is isosceles.
*Drawing from the orthogonal segment to , from the straight line tangent to the upper circle, and calling the meeting point, one sees that is a
This demonstration uses the rolling-wheel definition of cycloid, as well as the instantaneous velocity vector of a moving point, tangent to its trajectory. In the adjacent picture, and are two points belonging to two rolling circles, with the base of the first just above the top of the second. Initially, and coincide at the intersection point of the two circles. When the circles roll horizontally with the same speed, and traverse two cycloid curves. Considering the red line connecting and at a given time, one proves ''the line is always'' ''tangent to the lower arc at and orthogonal to the upper arc at ''. Let be the point in common between the upper and lower circles at the given time. Then:
* are colinear: indeed the equal rolling speed gives equal angles , and thus . The point lies on the line therefore and analogously . From the equality of and one has that also . It follows .
*If is the meeting point between the perpendicular from to the line segment and the tangent to the circle at , then the triangle is isosceles, as is easily seen from the construction: and . For the previous noted equality between and then and is isosceles.
*Drawing from the orthogonal segment to , from the straight line tangent to the upper circle, and calling the meeting point, one sees that is a rhombus
In plane Euclidean geometry, a rhombus (plural rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. Th ...
using the theorems on angles between parallel lines
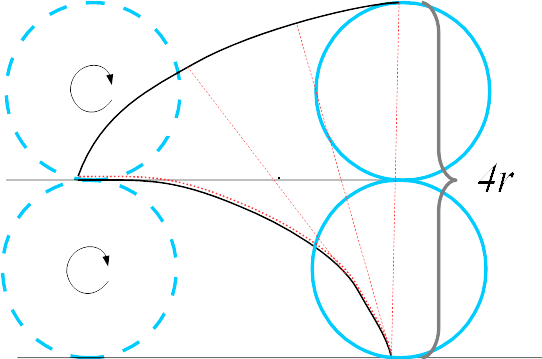
*Now consider the velocity of . It can be seen as the sum of two components, the rolling velocity and the drifting velocity , which are equal in modulus because the circles roll without skidding. is parallel to , while is tangent to the lower circle at and therefore is parallel to . The rhombus constituted from the components and is therefore similar (same angles) to the rhombus because they have parallel sides. Then , the total velocity of , is parallel to because both are diagonals of two rhombuses with parallel sides and has in common with the contact point . Thus the velocity vector lies on the prolongation of . Because is tangent to the cycloid at , it follows that also coincides with the tangent to the lower cycloid at .
*Analogously, it can be easily demonstrated that is orthogonal to (the other diagonal of the rhombus).
*This proves that the tip of a wire initially stretched on a half arch of the lower cycloid and fixed to the upper circle at will follow the point along its path ''without changing its length'' because the speed of the tip is at each moment orthogonal to the wire (no stretching or compression). The wire will be at the same time tangent at to the lower arc because of the tension and the facts demonstrated above. (If it were not tangent there would be a discontinuity at and consequently unbalanced tension forces.)
Area
Using the above parameterization , the area under one arch, is given by: This is three times the area of the rolling circle. This and similar results can be obtained geometrically without calculation by Mamikon's visual calculus.Arc length
 The
The arc length
ARC may refer to:
Business
* Aircraft Radio Corporation, a major avionics manufacturer from the 1920s to the '50s
* Airlines Reporting Corporation, an airline-owned company that provides ticket distribution, reporting, and settlement services
...
of one arch is given by
Another geometric way to calculate the length of the cycloid is to notice that when a wire describing an involute
In mathematics, an involute (also known as an evolvent) is a particular type of curve that is dependent on another shape or curve. An involute of a curve is the locus of a point on a piece of taut string as the string is either unwrapped from o ...
has been completely unwrapped from half an arch, it extends itself along two diameters, a length of . This is thus equal to half the length of arch, and that of a complete arch is .
Cycloidal pendulum
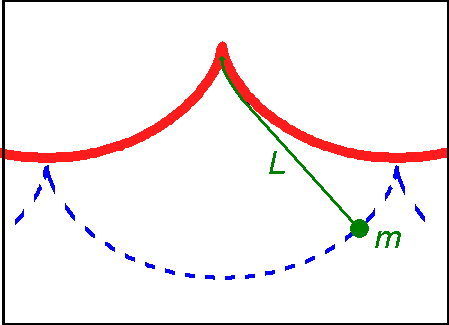
 If a simple pendulum is suspended from the cusp of an inverted cycloid, such that the string is constrained to be tangent to one of its arches, and the pendulum's length ''L'' is equal to that of half the arc length of the cycloid (i.e., twice the diameter of the generating circle, ''L = 4r''), the bob of the
If a simple pendulum is suspended from the cusp of an inverted cycloid, such that the string is constrained to be tangent to one of its arches, and the pendulum's length ''L'' is equal to that of half the arc length of the cycloid (i.e., twice the diameter of the generating circle, ''L = 4r''), the bob of the pendulum
A pendulum is a weight suspended from a wikt:pivot, pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, Mechanical equilibrium, equilibrium position, it is subject to a restoring force due to gravity that ...
also traces a cycloid path. Such a pendulum is isochronous, with equal-time swings regardless of amplitude. Introducing a coordinate system centred in the position of the cusp, the equation of motion is given by:
where is the angle that the straight part of the string makes with the vertical axis, and is given by
where is the "amplitude", is the radian frequency of the pendulum and ''g'' the gravitational acceleration.
 The 17th-century Dutch mathematician
The 17th-century Dutch mathematician Christiaan Huygens
Christiaan Huygens, Lord of Zeelhem, ( , , ; also spelled Huyghens; la, Hugenius; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor, who is regarded as one of the greatest scientists ...
discovered and proved these properties of the cycloid while searching for more accurate pendulum clock designs to be used in navigation.
Related curves
Several curves are related to the cycloid. *Trochoid
In geometry, a trochoid () is a roulette curve formed by a circle rolling along a line. It is the curve traced out by a point fixed to a circle (where the point may be on, inside, or outside the circle) as it rolls along a straight line. If the ...
: generalization of a cycloid in which the point tracing the curve may be inside the rolling circle (curtate) or outside (prolate).
* Hypocycloid
In geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle. As the radius of the larger circle is increased, the hypocycloid becomes more like the cycloid ...
: variant of a cycloid in which a circle rolls on the inside of another circle instead of a line.
* Epicycloid
In geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point on the circumference of a circle—called an ''epicycle''—which rolls without slipping around a fixed circle. It is a particular kind of roulette.
Equati ...
: variant of a cycloid in which a circle rolls on the outside of another circle instead of a line.
* Hypotrochoid: generalization of a hypocycloid where the generating point may not be on the edge of the rolling circle.
* Epitrochoid
In geometry, an epitrochoid ( or ) is a roulette traced by a point attached to a circle of radius rolling around the outside of a fixed circle of radius , where the point is at a distance from the center of the exterior circle.
The parametric ...
: generalization of an epicycloid where the generating point may not be on the edge of the rolling circle.
All these curves are roulettes
The Roulettes are the Royal Australian Air Force's formation aerobatic display team.
They provide about 150 flying displays a year, in Australia and in friendly countries around the Southeast Asian region. The Roulettes form part of the RAA ...
with a circle rolled along another curve of uniform curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
For curves, the can ...
. The cycloid, epicycloids, and hypocycloids have the property that each is similar to its evolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. That is to say that when the center of curvature of each point on a curve is drawn, the resultant shape will be the evolute of that c ...
. If ''q'' is the product
Product may refer to:
Business
* Product (business), an item that serves as a solution to a specific consumer problem.
* Product (project management), a deliverable or set of deliverables that contribute to a business solution
Mathematics
* Prod ...
of that curvature with the circle's radius, signed positive for epi- and negative for hypo-, then the similitude ratio of curve to evolute is 1 + 2''q''.
The classic Spirograph
Spirograph is a geometric drawing device that produces mathematical roulette curves of the variety technically known as hypotrochoids and epitrochoids. The well-known toy version was developed by British engineer Denys Fisher and first sold ...
toy traces out hypotrochoid and epitrochoid
In geometry, an epitrochoid ( or ) is a roulette traced by a point attached to a circle of radius rolling around the outside of a fixed circle of radius , where the point is at a distance from the center of the exterior circle.
The parametric ...
curves.
Other uses
 The cycloidal arch was used by architect
The cycloidal arch was used by architect Louis Kahn
Louis Isadore Kahn (born Itze-Leib Schmuilowsky; – March 17, 1974) was an Estonian-born American architect based in Philadelphia. After working in various capacities for several firms in Philadelphia, he founded his own atelier in 1935. Whi ...
in his design for the Kimbell Art Museum
The Kimbell Art Museum in Fort Worth, Texas, hosts an art collection as well as traveling art exhibitions, educational programs and an extensive research library. Its initial artwork came from the private collection of Kay and Velma Kimbell, w ...
in Fort Worth, Texas
Fort Worth is the List of cities in Texas by population, fifth-largest city in the U.S. state of Texas and the List of United States cities by population, 13th-largest city in the United States. It is the county seat of Tarrant County, Texas, T ...
. It was also used by Wallace K. Harrison in the design of the Hopkins Center at Dartmouth College
Dartmouth College (; ) is a private research university in Hanover, New Hampshire. Established in 1769 by Eleazar Wheelock, it is one of the nine colonial colleges chartered before the American Revolution. Although founded to educate Native ...
in Hanover, New Hampshire
Hanover is a town located along the Connecticut River in Grafton County, New Hampshire, United States. As of the 2020 census, its population was 11,870. The town is home to the Ivy League university Dartmouth College, the U.S. Army Corps of ...
.
Early research indicated that some transverse arching curves of the plates of golden age violins are closely modeled by curtate cycloid curves. Later work indicates that curtate cycloids do not serve as general models for these curves, which vary considerably.
See also
* Cyclogon *Cycloid gear
The cycloidal gear profile is a form of toothed gear used in mechanical clocks, rather than the involute gear form used for most other gears. The gear tooth profile is based on the epicycloid and hypocycloid curves, which are the curves genera ...
* List of periodic functions
* Tautochrone curve
A tautochrone or isochrone curve (from Greek prefixes tauto- meaning ''same'' or iso- ''equal'', and chrono ''time'') is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independ ...
References
Further reading
* ''An application from physics'': Ghatak, A. & Mahadevan, L. Crack street: the cycloidal wake of acylinder
A cylinder (from ) has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.
A cylinder may also be defined as an infi ...
tearing through a sheet. Physical Review Letters, 91, (2003)link.aps.org
* Edward Kasner & James Newman (1940) Mathematics and the Imagination, pp 196–200,
Simon & Schuster
Simon & Schuster () is an American publishing company and a subsidiary of Paramount Global. It was founded in New York City on January 2, 1924 by Richard L. Simon and M. Lincoln Schuster. As of 2016, Simon & Schuster was the third largest pub ...
.
*
External links
* * Retrieved April 27, 2007.Cycloids
at cut-the-knot
A Treatise on The Cycloid and all forms of Cycloidal Curves
monograph by Richard A. Proctor, B.A. posted b
*
Cycloid Curves
' by Sean Madsen with contributions by David von Seggern,
Wolfram Demonstrations Project
The Wolfram Demonstrations Project is an organized, open-source collection of small (or medium-size) interactive programs called Demonstrations, which are meant to visually and interactively represent ideas from a range of fields. It is hos ...
.
Cycloid on PlanetPTC (Mathcad)
by Tom Apostol {{Authority control Roulettes (curve)