compass and straightedge on:
[Wikipedia]
[Google]
[Amazon]
 In
In
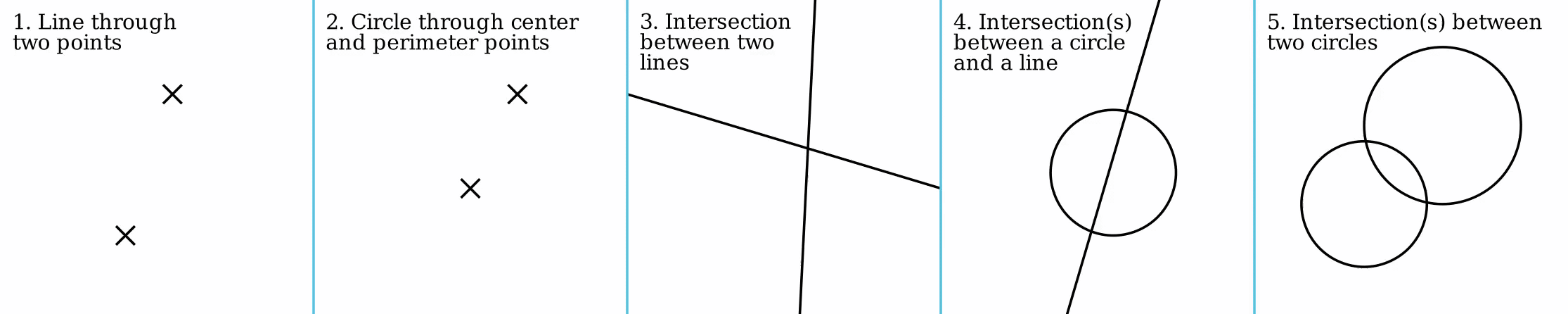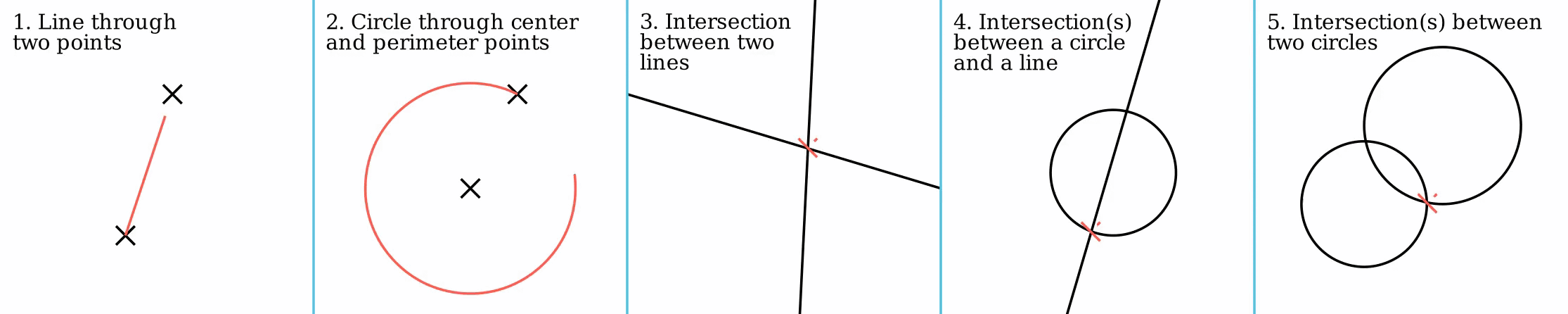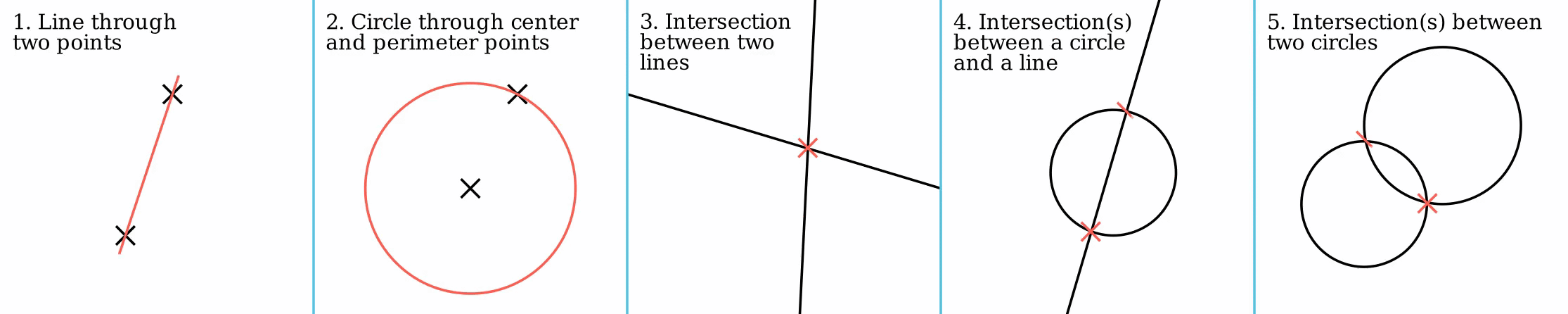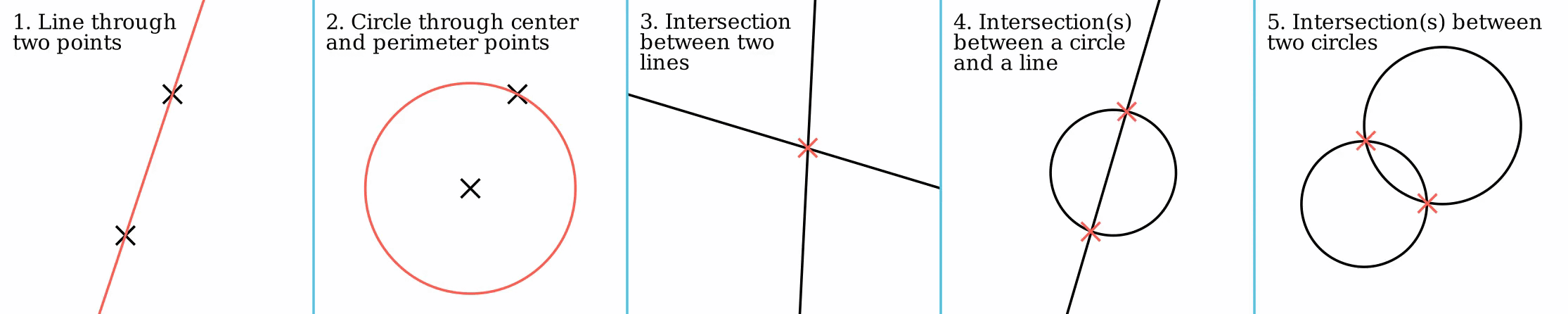 All straightedge-and-compass constructions consist of repeated application of five basic constructions using the points, lines and circles that have already been constructed. These are:
*Creating the line through two points
*Creating the
All straightedge-and-compass constructions consist of repeated application of five basic constructions using the points, lines and circles that have already been constructed. These are:
*Creating the line through two points
*Creating the
 Some
Some
Archimedes' trisection
or extract an arbitrary cube root (due to Nicomedes). Hence, any distance whose ratio to an existing distance is the solution of a
 Given a straight line segment called AB, could this be divided in three new equal segments and in many parts required by the use of
Given a straight line segment called AB, could this be divided in three new equal segments and in many parts required by the use of
Regular polygon constructions
by Dr. Math at ''The Math Forum @ Drexel''
Construction with the Compass Only
at ''
Angle Trisection by Hippocrates
at ''cut-the-knot'' * {{Authority control Greek mathematics
 In
In geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
s, and other geometric figures using only an idealized ruler
A ruler, sometimes called a rule, scale, line gauge, or metre/meter stick, is an instrument used to make length measurements, whereby a length is read from a series of markings called "rules" along an edge of the device. Usually, the instr ...
and a compass
A compass is a device that shows the cardinal directions used for navigation and geographic orientation. It commonly consists of a magnetized needle or other element, such as a compass card or compass rose, which can pivot to align itself with No ...
.
The idealized ruler, known as a straightedge
A straightedge or straight edge is a tool used for drawing straight lines, or checking their straightness. If it has equally spaced markings along its length, it is usually called a ruler.
Straightedges are used in the automotive service and ma ...
, is assumed to be infinite in length, have only one edge, and no markings on it. The compass is assumed to have no maximum or minimum radius, and is assumed to "collapse" when lifted from the page, so it may not be directly used to transfer distances. (This is an unimportant restriction since, using a multi-step procedure, a distance can be transferred even with a collapsing compass; see compass equivalence theorem. Note however that whilst a non-collapsing compass held against a straightedge might seem to be equivalent to marking it, the neusis construction is still impermissible and this is what unmarked really means: see Markable rulers below.) More formally, the only permissible constructions are those granted by the first three postulates of Euclid's ''Elements''.
It turns out to be the case that every point constructible using straightedge and compass may also be constructed using compass alone, or by straightedge alone if given a single circle and its center.
Ancient Greek mathematicians first conceived straightedge-and-compass constructions, and a number of ancient problems in plane geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set ...
impose this restriction. The ancient Greeks developed many constructions, but in some cases were unable to do so. Gauss
Johann Carl Friedrich Gauss (; ; ; 30 April 177723 February 1855) was a German mathematician, astronomer, Geodesy, geodesist, and physicist, who contributed to many fields in mathematics and science. He was director of the Göttingen Observat ...
showed that some polygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain.
The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon ...
s are constructible but that most are not. Some of the most famous straightedge-and-compass problems were proved impossible by Pierre Wantzel in 1837 using field theory, namely trisecting an arbitrary angle and doubling the volume of a cube (see § impossible constructions). Many of these problems are easily solvable provided that other geometric transformations are allowed; for example, neusis construction can be used to solve the former two problems.
In terms of algebra
Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic ope ...
, a length is constructible if and only if
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either bo ...
it represents a constructible number, and an angle is constructible if and only if its cosine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that ...
is a constructible number. A number is constructible if and only if it can be written using the four basic arithmetic operations and the extraction of square root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4 ...
s but of no higher-order roots.
Straightedge and compass tools
The "straightedge" and "compass" of straightedge-and-compass constructions are idealized versions of real-world rulers and compasses. *The straightedge is an infinitely long edge with no markings on it. It can only be used to draw a line segment between two points or to extend an existing line segment. *The compass can have an arbitrarily large radius with no markings on it (unlike certain real-world compasses). Circles and circular arcs can be drawn starting from two given points: the centre and a point on the circle. The compass may or may not collapse (i.e. fold after being taken off the page, erasing its 'stored' radius). *Lines and circles constructed have infinite precision and zero width. Actual compasses do not collapse and modern geometric constructions often use this feature. A 'collapsing compass' would appear to be a less powerful instrument. However, by the compass equivalence theorem in Proposition 2 of Book 1 ofEuclid's Elements
The ''Elements'' ( ) is a mathematics, mathematical treatise written 300 BC by the Ancient Greek mathematics, Ancient Greek mathematician Euclid.
''Elements'' is the oldest extant large-scale deductive treatment of mathematics. Drawing on the w ...
, no power is lost by using a collapsing compass. Although the proposition is correct, its proofs have a long and checkered history. In any case, the equivalence is why this feature is not stipulated in the definition of the ideal compass.
Each construction must be mathematically ''exact''. "Eyeballing" distances (looking at the construction and guessing at its accuracy) or using markings on a ruler are not permitted. Each construction must also ''terminate''. That is, it must have a finite number of steps and not be the limit of ever closer approximations. (If an unlimited number of steps is permitted, some otherwise-impossible constructions become possible by means of infinite sequences converging to a limit.)
Stated this way, straightedge-and-compass constructions appear to be a parlour game
A parlour or parlor game is a group game played indoors, named so as they were often played in a parlour. These games were extremely popular among the upper and middle classes in the United Kingdom and in the United States during the Victorian er ...
, rather than a serious practical problem; but the purpose of the restriction is to ensure that constructions can be ''proven'' to be ''exactly'' correct.
History
The ancient Greek mathematicians first attempted straightedge-and-compass constructions, and they discovered how to constructsums
In mathematics, summation is the addition of a sequence of numbers, called ''addends'' or ''summands''; the result is their ''sum'' or ''total''. Beside numbers, other types of values can be summed as well: functions, vectors, matrices, polynom ...
, differences, products
Product may refer to:
Business
* Product (business), an item that can be offered to a market to satisfy the desire or need of a customer.
* Product (project management), a deliverable or set of deliverables that contribute to a business solution
...
, ratio
In mathematics, a ratio () shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
s, and square root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4 ...
s of given lengths. They could also construct half of a given angle, a square whose area is twice that of another square, a square having the same area as a given polygon, and regular polygons
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex ...
of 3, 4, or 5 sides (or one with twice the number of sides of a given polygon). But they could not construct one third of a given angle except in particular cases, or a square with the same area as a given circle, or regular polygons with other numbers of sides.Bold, Benjamin. ''Famous Problems of Geometry and How to Solve Them'', Dover Publications, 1982 (orig. 1969). Nor could they construct the side of a cube whose volume is twice the volume of a cube with a given side.
Hippocrates
Hippocrates of Kos (; ; ), also known as Hippocrates II, was a Greek physician and philosopher of the Classical Greece, classical period who is considered one of the most outstanding figures in the history of medicine. He is traditionally referr ...
and Menaechmus
Menaechmus (, c. 380 – c. 320 BC) was an ancient Greek mathematician, list of geometers, geometer and philosopher born in Alopeconnesus or Prokonnesos in the Thracian Chersonese, who was known for his friendship with the renowned philosopher P ...
showed that the volume of the cube could be doubled by finding the intersections of hyperbola
In mathematics, a hyperbola is a type of smooth function, smooth plane curve, curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected component ( ...
s and parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactl ...
s, but these cannot be constructed by straightedge and compass. In the fifth century BCE, Hippias used a curve that he called a quadratrix to both trisect the general angle and square the circle, and Nicomedes in the second century BCE showed how to use a conchoid to trisect an arbitrary angle; but these methods also cannot be followed with just straightedge and compass.
No progress on the unsolved problems was made for two millennia, until in 1796 Gauss
Johann Carl Friedrich Gauss (; ; ; 30 April 177723 February 1855) was a German mathematician, astronomer, Geodesy, geodesist, and physicist, who contributed to many fields in mathematics and science. He was director of the Göttingen Observat ...
showed that a regular polygon with 17 sides could be constructed; five years later he showed the sufficient criterion for a regular polygon of ''n'' sides to be constructible.
In 1837 Pierre Wantzel published a proof of the impossibility of trisecting an arbitrary angle or of doubling the volume of a cube, based on the impossibility of constructing cube root
In mathematics, a cube root of a number is a number that has the given number as its third power; that is y^3=x. The number of cube roots of a number depends on the number system that is considered.
Every real number has exactly one real cub ...
s of lengths. He also showed that Gauss's sufficient constructibility condition for regular polygons is also necessary.
Then in 1882 Lindemann showed that is a transcendental number
In mathematics, a transcendental number is a real or complex number that is not algebraic: that is, not the root of a non-zero polynomial with integer (or, equivalently, rational) coefficients. The best-known transcendental numbers are and . ...
, and thus that it is impossible by straightedge and compass to construct a square with the same area as a given circle.
The basic constructions
 All straightedge-and-compass constructions consist of repeated application of five basic constructions using the points, lines and circles that have already been constructed. These are:
*Creating the line through two points
*Creating the
All straightedge-and-compass constructions consist of repeated application of five basic constructions using the points, lines and circles that have already been constructed. These are:
*Creating the line through two points
*Creating the circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
that contains one point and has a center at another point
*Creating the point at the intersection
In mathematics, the intersection of two or more objects is another object consisting of everything that is contained in all of the objects simultaneously. For example, in Euclidean geometry, when two lines in a plane are not parallel, their ...
of two (non-parallel) lines
*Creating the one point or two points in the intersection of a line and a circle (if they intersect)
*Creating the one point or two points in the intersection of two circles (if they intersect).
For example, starting with just two distinct points, we can create a line or either of two circles (in turn, using each point as centre and passing through the other point). If we draw both circles, two new points are created at their intersections. Drawing lines between the two original points and one of these new points completes the construction of an equilateral triangle.
Therefore, in any geometric problem we have an initial set of symbols (points and lines), an algorithm, and some results. From this perspective, geometry is equivalent to an axiomatic algebra
Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic ope ...
, replacing its elements by symbols. Probably Gauss
Johann Carl Friedrich Gauss (; ; ; 30 April 177723 February 1855) was a German mathematician, astronomer, Geodesy, geodesist, and physicist, who contributed to many fields in mathematics and science. He was director of the Göttingen Observat ...
first realized this, and used it to prove the impossibility of some constructions; only much later did Hilbert
David Hilbert (; ; 23 January 1862 – 14 February 1943) was a German mathematician and philosophy of mathematics, philosopher of mathematics and one of the most influential mathematicians of his time.
Hilbert discovered and developed a broad ...
find a complete set of axioms for geometry.
Common straightedge-and-compass constructions
The most-used straightedge-and-compass constructions include: * Constructing the perpendicular bisector from a segment * Finding themidpoint
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.
Formula
The midpoint of a segment in ''n''-dim ...
of a segment.
* Drawing a perpendicular line from a point to a line.
* Bisecting an angle
* Mirroring a point in a line
* Constructing a line through a point tangent to a circle
* Constructing a circle through 3 noncollinear points
* Drawing a line through a given point parallel to a given line.
Constructible points
One can associate an algebra to our geometry using aCartesian coordinate system
In geometry, a Cartesian coordinate system (, ) in a plane (geometry), plane is a coordinate system that specifies each point (geometry), point uniquely by a pair of real numbers called ''coordinates'', which are the positive and negative number ...
made of two lines, and represent points of our plane by vector
Vector most often refers to:
* Euclidean vector, a quantity with a magnitude and a direction
* Disease vector, an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematics a ...
s. Finally we can write these vectors as complex numbers.
Using the equations for lines and circles, one can show that the points at which they intersect lie in a quadratic extension
In mathematics, the term quadratic describes something that pertains to squares, to the operation of squaring, to terms of the second degree, or equations or formulas that involve such terms. ''Quadratus'' is Latin for ''square''.
Mathematics ...
of the smallest field ''F'' containing two points on the line, the center of the circle, and the radius of the circle. That is, they are of the form , where ''x'', ''y'', and ''k'' are in ''F''.
Since the field of constructible points is closed under ''square roots'', it contains all points that can be obtained by a finite sequence of quadratic extensions of the field of complex numbers with rational coefficients. By the above paragraph, one can show that any constructible point can be obtained by such a sequence of extensions. As a corollary of this, one finds that the degree of the minimal polynomial for a constructible point (and therefore of any constructible length) is a power of 2. In particular, any constructible point (or length) is an algebraic number
In mathematics, an algebraic number is a number that is a root of a function, root of a non-zero polynomial in one variable with integer (or, equivalently, Rational number, rational) coefficients. For example, the golden ratio (1 + \sqrt)/2 is ...
, though not every algebraic number is constructible; for example, is algebraic but not constructible.
Constructible angles
There is abijection
In mathematics, a bijection, bijective function, or one-to-one correspondence is a function between two sets such that each element of the second set (the codomain) is the image of exactly one element of the first set (the domain). Equival ...
between the angles that are constructible and the points that are constructible on any constructible circle. The angles that are constructible form an abelian group
In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is commu ...
under addition modulo 2π (which corresponds to multiplication of the points on the unit circle viewed as complex numbers). The angles that are constructible are exactly those whose tangent (or equivalently, sine or cosine) is constructible as a number. For example, the regular heptadecagon
In geometry, a heptadecagon, septadecagon or 17-gon is a seventeen-sided polygon.
Regular heptadecagon
A ''regular polygon, regular heptadecagon'' is represented by the Schläfli symbol .
Construction
As 17 is a Fermat prime, the regular he ...
(the seventeen-sided regular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex ...
) is constructible because
:
as discovered by Gauss
Johann Carl Friedrich Gauss (; ; ; 30 April 177723 February 1855) was a German mathematician, astronomer, Geodesy, geodesist, and physicist, who contributed to many fields in mathematics and science. He was director of the Göttingen Observat ...
.
The group of constructible angles is closed under the operation that halves angles (which corresponds to taking square roots in the complex numbers). The only angles of finite order that may be constructed starting with two points are those whose order is either a power of two, or a product of a power of two and a set of distinct Fermat primes. In addition there is a dense set of constructible angles of infinite order.
Relation to complex arithmetic
Given a set of points in theEuclidean plane
In mathematics, a Euclidean plane is a Euclidean space of Two-dimensional space, dimension two, denoted \textbf^2 or \mathbb^2. It is a geometric space in which two real numbers are required to determine the position (geometry), position of eac ...
, selecting any one of them to be called 0 and another to be called 1, together with an arbitrary choice of orientation
Orientation may refer to:
Positioning in physical space
* Map orientation, the relationship between directions on a map and compass directions
* Orientation (housing), the position of a building with respect to the sun, a concept in building des ...
allows us to consider the points as a set of complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s.
Given any such interpretation of a set of points as complex numbers, the points constructible using valid straightedge-and-compass constructions alone are precisely the elements of the smallest field containing the original set of points and closed under the complex conjugate
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, if a and b are real numbers, then the complex conjugate of a + bi is a - ...
and square root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4 ...
operations (to avoid ambiguity, we can specify the square root with complex argument less than π). The elements of this field are precisely those that may be expressed as a formula in the original points using only the operations of addition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol, +) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication, and Division (mathematics), divis ...
, subtraction
Subtraction (which is signified by the minus sign, –) is one of the four Arithmetic#Arithmetic operations, arithmetic operations along with addition, multiplication and Division (mathematics), division. Subtraction is an operation that repre ...
, multiplication
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division (mathematics), division. The result of a multiplication operation is called a ''Product (mathem ...
, division, complex conjugate
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, if a and b are real numbers, then the complex conjugate of a + bi is a - ...
, and square root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4 ...
, which is easily seen to be a countable dense subset of the plane. Each of these six operations corresponding to a simple straightedge-and-compass construction. From such a formula it is straightforward to produce a construction of the corresponding point by combining the constructions for each of the arithmetic operations. More efficient constructions of a particular set of points correspond to shortcuts in such calculations.
Equivalently (and with no need to arbitrarily choose two points) we can say that, given an arbitrary choice of orientation, a set of points determines a set of complex ratios given by the ratios of the differences between any two pairs of points. The set of ratios constructible using straightedge and compass from such a set of ratios is precisely the smallest field containing the original ratios and closed under taking complex conjugates and square roots.
For example, the real part, imaginary part and modulus of a point or ratio ''z'' (taking one of the two viewpoints above) are constructible as these may be expressed as
:
:
:
''Doubling the cube'' and ''trisection of an angle'' (except for special angles such as any ''φ'' such that ''φ''/(2)) is a rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for example,
The set of all ...
with denominator
A fraction (from , "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight-fifths, thre ...
not divisible by 3) require ratios which are the solution to cubic equation
In algebra, a cubic equation in one variable is an equation of the form
ax^3+bx^2+cx+d=0
in which is not zero.
The solutions of this equation are called roots of the cubic function defined by the left-hand side of the equation. If all of th ...
s, while ''squaring the circle'' requires a transcendental ratio. None of these are in the fields described, hence no straightedge-and-compass construction for these exists.
Impossible constructions
The ancient Greeks thought that the construction problems they could not solve were simply obstinate, not unsolvable. With modern methods, however, these straightedge-and-compass constructions have been shown to be logically impossible to perform. (The problems themselves, however, are solvable, and the Greeks knew how to solve them without the constraint of working only with straightedge and compass.)Squaring the circle
The most famous of these problems,squaring the circle
Squaring the circle is a problem in geometry first proposed in Greek mathematics. It is the challenge of constructing a square (geometry), square with the area of a circle, area of a given circle by using only a finite number of steps with a ...
, otherwise known as the quadrature of the circle, involves constructing a square with the same area as a given circle using only straightedge and compass.
Squaring the circle has been proved impossible, as it involves generating a transcendental number
In mathematics, a transcendental number is a real or complex number that is not algebraic: that is, not the root of a non-zero polynomial with integer (or, equivalently, rational) coefficients. The best-known transcendental numbers are and . ...
, that is, . Only certain algebraic number
In mathematics, an algebraic number is a number that is a root of a function, root of a non-zero polynomial in one variable with integer (or, equivalently, Rational number, rational) coefficients. For example, the golden ratio (1 + \sqrt)/2 is ...
s can be constructed with ruler and compass alone, namely those constructed from the integers with a finite sequence of operations of addition, subtraction, multiplication, division, and taking square roots. The phrase "squaring the circle" is often used to mean "doing the impossible" for this reason.
Without the constraint of requiring solution by ruler and compass alone, the problem is easily solvable by a wide variety of geometric and algebraic means, and was solved many times in antiquity.
A method which comes very close to approximating the "quadrature of the circle" can be achieved using a Kepler triangle.
Doubling the cube
Doubling the cube is the construction, using only a straightedge and compass, of the edge of a cube that has twice the volume of a cube with a given edge. This is impossible because the cube root of 2, though algebraic, cannot be computed from integers by addition, subtraction, multiplication, division, and taking square roots. This follows because its minimal polynomial over the rationals has degree 3. This construction is possible using a straightedge with two marks on it and a compass.Angle trisection
Angle trisection is the construction, using only a straightedge and a compass, of an angle that is one-third of a given arbitrary angle. This is impossible in the general case. For example, the angle 2/5radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at ...
s (72° = 360°/5) can be trisected, but the angle of /3 radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at ...
s (60 °) cannot be trisected. The general trisection problem is also easily solved when a straightedge with two marks on it is allowed (a neusis
In geometry, the neusis (; ; plural: ) is a geometric construction method that was used in antiquity by Greek mathematics, Greek mathematicians.
Geometric construction
The neusis construction consists of fitting a line element of given length ...
construction).
Distance to an ellipse
The line segment from any point in the plane to the nearest point on acircle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
can be constructed, but the segment from any point in the plane to the nearest point on an ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special ty ...
of positive eccentricity
Eccentricity or eccentric may refer to:
* Eccentricity (behavior), odd behavior on the part of a person, as opposed to being "normal"
Mathematics, science and technology Mathematics
* Off-Centre (geometry), center, in geometry
* Eccentricity (g ...
cannot in general be constructed. See Note that results proven here are mostly a consequence of the non-constructivity of conics. If the initial conic is considered as a given, then the proof must be reviewed to check if other distinct conic needs to be generated. As an example, constructions for normals of a parabola are known, but they need to use an intersection between circle and the parabola itself. So they are not constructible in the sense that the parabola is not constructible.
Alhazen's problem
In 1997, theOxford
Oxford () is a City status in the United Kingdom, cathedral city and non-metropolitan district in Oxfordshire, England, of which it is the county town.
The city is home to the University of Oxford, the List of oldest universities in continuou ...
mathematician Peter M. Neumann proved the theorem that there is no ruler-and-compass construction for the general solution of the ancient Alhazen's problem (billiard problem or reflection from a spherical mirror).
Constructing regular polygons
 Some
Some regular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex ...
s (e.g. a pentagon
In geometry, a pentagon () is any five-sided polygon or 5-gon. The sum of the internal angles in a simple polygon, simple pentagon is 540°.
A pentagon may be simple or list of self-intersecting polygons, self-intersecting. A self-intersecting ...
) are easy to construct with straightedge and compass; others are not. This led to the question: Is it possible to construct all regular polygons with straightedge and compass?
Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; ; ; 30 April 177723 February 1855) was a German mathematician, astronomer, geodesist, and physicist, who contributed to many fields in mathematics and science. He was director of the Göttingen Observatory and ...
in 1796 showed that a regular 17-sided polygon can be constructed, and five years later showed that a regular ''n''-sided polygon can be constructed with straightedge and compass if the odd prime factor
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
s of ''n'' are distinct Fermat prime
In mathematics, a Fermat number, named after Pierre de Fermat (1601–1665), the first known to have studied them, is a positive integer of the form:F_ = 2^ + 1, where ''n'' is a non-negative integer. The first few Fermat numbers are: 3, 5, ...
s. Gauss conjecture
In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis or Fermat's conjecture (now a theorem, proven in 1995 by Andrew Wiles), ha ...
d that this condition was also necessary; the conjecture was proven by Pierre Wantzel in 1837.
The first few constructible regular polygons have the following numbers of sides:
: 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272...
There are known to be an infinitude of constructible regular polygons with an even number of sides (because if a regular ''n''-gon is constructible, then so is a regular 2''n''-gon and hence a regular 4''n''-gon, 8''n''-gon, etc.). However, there are only 5 known Fermat primes, giving only 31 known constructible regular ''n''-gons with an odd number of sides.
Constructing a triangle from three given characteristic points or lengths
Sixteen key points of atriangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimension ...
are its vertices, the midpoints of its sides, the feet of its altitudes
Altitude is a distance measurement, usually in the vertical or "up" direction, between a reference datum and a point or object. The exact definition and reference datum varies according to the context (e.g., aviation, geometry, geographical s ...
, the feet of its internal angle bisectors, and its circumcenter
In geometry, the circumscribed circle or circumcircle of a triangle is a circle that passes through all three vertices. The center of this circle is called the circumcenter of the triangle, and its radius is called the circumradius. The circumcen ...
, centroid
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the figure. The same definition extends to any object in n-d ...
, orthocenter
The orthocenter of a triangle, usually denoted by , is the point (geometry), point where the three (possibly extended) altitude (triangle), altitudes intersect. The orthocenter lies inside the triangle if and only if the triangle is acute trian ...
, and incenter
In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bis ...
. These can be taken three at a time to yield 139 distinct nontrivial problems of constructing a triangle from three points. Of these problems, three involve a point that can be uniquely constructed from the other two points; 23 can be non-uniquely constructed (in fact for infinitely many solutions) but only if the locations of the points obey certain constraints; in 74 the problem is constructible in the general case; and in 39 the required triangle exists but is not constructible.
Twelve key lengths of a triangle are the three side lengths, the three altitudes
Altitude is a distance measurement, usually in the vertical or "up" direction, between a reference datum and a point or object. The exact definition and reference datum varies according to the context (e.g., aviation, geometry, geographical s ...
, the three medians, and the three angle bisectors. Together with the three angles, these give 95 distinct combinations, 63 of which give rise to a constructible triangle, 30 of which do not, and two of which are underdefined.
Restricted constructions
Various attempts have been made to restrict the allowable tools for constructions under various rules, in order to determine what is still constructible and how it may be constructed, as well as determining the minimum criteria necessary to still be able to construct everything that compass and straightedge can.Constructing with only ruler or only compass
It is possible (according to the Mohr–Mascheroni theorem) to construct anything with just a compass if it can be constructed with a ruler and compass, provided that the given data and the data to be found consist of discrete points (not lines or circles). The truth of this theorem depends on the truth of Archimedes' axiom, which is not first-order in nature. Examples of compass-only constructions include Napoleon's problem. It is impossible to take a square root with just a ruler, so some things that cannot be constructed with a ruler can be constructed with a compass; but (by thePoncelet–Steiner theorem
In the branch of mathematics known as Euclidean geometry, the Poncelet–Steiner theorem is one of several results concerning compass and straightedge constructions having additional restrictions imposed on the traditional rules. This result, rela ...
) given a single circle and its center, they can be constructed.
Extended constructions
The ancient Greeks classified constructions into three major categories, depending on the complexity of the tools required for their solution. If a construction used only a straightedge and compass, it was called planar; if it also required one or more conic sections (other than the circle), then it was called solid; the third category included all constructions that did not fall into either of the other two categories. This categorization meshes nicely with the modern algebraic point of view. A complex number that can be expressed using only the field operations and square roots (as described above) has a planar construction. A complex number that includes also the extraction of cube roots has a solid construction. In the language of fields, a complex number that is planar has degree a power of two, and lies in afield extension
In mathematics, particularly in algebra, a field extension is a pair of fields K \subseteq L, such that the operations of ''K'' are those of ''L'' restricted to ''K''. In this case, ''L'' is an extension field of ''K'' and ''K'' is a subfield of ...
that can be broken down into a tower of fields where each extension has degree two. A complex number that has a solid construction has degree with prime factors of only two and three, and lies in a field extension that is at the top of a tower of fields where each extension has degree 2 or 3.
Solid constructions
A point has a solid construction if it can be constructed using a straightedge, compass, and a (possibly hypothetical) conic drawing tool that can draw any conic with already constructed focus, directrix, and eccentricity. The same set of points can often be constructed using a smaller set of tools. For example, using a compass, straightedge, and a piece of paper on which we have the parabola y=x2 together with the points (0,0) and (1,0), one can construct any complex number that has a solid construction. Likewise, a tool that can draw any ellipse with already constructed foci and major axis (think two pins and a piece of string) is just as powerful. The ancient Greeks knew that doubling the cube and trisecting an arbitrary angle both had solid constructions.Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
gave a neusis
In geometry, the neusis (; ; plural: ) is a geometric construction method that was used in antiquity by Greek mathematics, Greek mathematicians.
Geometric construction
The neusis construction consists of fitting a line element of given length ...
construction of the regular heptagon
In geometry, a heptagon or septagon is a seven-sided polygon or 7-gon.
The heptagon is sometimes referred to as the septagon, using ''Wikt:septa-, septa-'' (an elision of ''Wikt:septua-, septua-''), a Latin-derived numerical prefix, rather than ...
, which was interpreted by medieval Arabic commentators, Bartel Leendert van der Waerden
Bartel Leendert van der Waerden (; 2 February 1903 – 12 January 1996) was a Dutch mathematician and historian of mathematics.
Biography
Education and early career
Van der Waerden learned advanced mathematics at the University of Amste ...
, and others as being based on a solid construction, but this has been disputed, as other interpretations are possible. The quadrature of the circle does not have a solid construction.
A regular ''n''-gon has a solid construction if and only if ''n''=2''a''3''b''''m'' where ''a'' and ''b'' are some non-negative integers and ''m'' is a product of zero or more distinct Pierpont prime
In number theory, a Pierpont prime is a prime number of the form
2^u\cdot 3^v + 1\,
for some nonnegative integers and . That is, they are the prime numbers for which is 3-smooth. They are named after the mathematician James Pierpont, who us ...
s (primes of the form 2''r''3''s''+1). Therefore, regular ''n''-gon admits a solid, but not planar, construction if and only if ''n'' is in the sequence
: 7, 9, 13, 14, 18, 19, 21, 26, 27, 28, 35, 36, 37, 38, 39, 42, 45, 52, 54, 56, 57, 63, 65, 70, 72, 73, 74, 76, 78, 81, 84, 90, 91, 95, 97...
The set of ''n'' for which a regular ''n''-gon has no solid construction is the sequence
: 11, 22, 23, 25, 29, 31, 33, 41, 43, 44, 46, 47, 49, 50, 53, 55, 58, 59, 61, 62, 66, 67, 69, 71, 75, 77, 79, 82, 83, 86, 87, 88, 89, 92, 93, 94, 98, 99, 100...
Like the question with Fermat primes, it is an open question as to whether there are an infinite number of Pierpont primes.
Angle trisection
What if, together with the straightedge and compass, we had a tool that could (only) trisect an arbitrary angle? Such constructions are solid constructions, but there exist numbers with solid constructions that cannot be constructed using such a tool. For example, we cannot double the cube with such a tool. On the other hand, every regular n-gon that has a solid construction can be constructed using such a tool.Origami
The mathematical theory of origami is more powerful than straightedge-and-compass construction. Folds satisfying the Huzita–Hatori axioms can construct exactly the same set of points as the extended constructions using a compass and conic drawing tool. Therefore,origami
) is the Japanese art of paper folding. In modern usage, the word "origami" is often used as an inclusive term for all folding practices, regardless of their culture of origin. The goal is to transform a flat square sheet of paper into a ...
can also be used to solve cubic equations (and hence quartic equations), and thus solve two of the classical problems.
Markable rulers
Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
, Nicomedes and Apollonius
Apollonius () is a masculine given name which may refer to:
People Ancient world Artists
* Apollonius of Athens (sculptor) (fl. 1st century BC)
* Apollonius of Tralles (fl. 2nd century BC), sculptor
* Apollonius (satyr sculptor)
* Apo ...
gave constructions involving the use of a markable ruler. This would permit them, for example, to take a line segment, two lines (or circles), and a point; and then draw a line which passes through the given point and intersects the two given lines, such that the distance between the points of intersection equals the given segment. This the Greeks called ''neusis'' ("inclination", "tendency" or "verging"), because the new line ''tends'' to the point.
In this expanded scheme, we can trisect an arbitrary angle (seArchimedes' trisection
or extract an arbitrary cube root (due to Nicomedes). Hence, any distance whose ratio to an existing distance is the solution of a
cubic
Cubic may refer to:
Science and mathematics
* Cube (algebra), "cubic" measurement
* Cube, a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex
** Cubic crystal system, a crystal system w ...
or a quartic equation
In mathematics, a quartic equation is one which can be expressed as a ''quartic function'' equaling zero. The general form of a quartic equation is
:ax^4+bx^3+cx^2+dx+e=0 \,
where ''a'' ≠ 0.
The quartic is the highest order polynom ...
is constructible. Using a markable ruler, regular polygons with solid constructions, like the heptagon
In geometry, a heptagon or septagon is a seven-sided polygon or 7-gon.
The heptagon is sometimes referred to as the septagon, using ''Wikt:septa-, septa-'' (an elision of ''Wikt:septua-, septua-''), a Latin-derived numerical prefix, rather than ...
, are constructible; and John H. Conway and Richard K. Guy give constructions for several of them.
The neusis construction is more powerful than a conic drawing tool, as one can construct complex numbers that do not have solid constructions. In fact, using this tool one can solve some quintics that are not solvable using radicals. It is known that one cannot solve an irreducible polynomial of prime degree greater or equal to 7 using the neusis construction, so it is not possible to construct a regular 23-gon or 29-gon using this tool. Benjamin and Snyder proved that it is possible to construct the regular 11-gon, but did not give a construction. It is still open as to whether a regular 25-gon or 31-gon is constructible using this tool.
Trisect a straight segment
 Given a straight line segment called AB, could this be divided in three new equal segments and in many parts required by the use of
Given a straight line segment called AB, could this be divided in three new equal segments and in many parts required by the use of intercept theorem
The intercept theorem, also known as Thales's theorem, basic proportionality theorem or side splitter theorem, is an important theorem in elementary geometry about the ratios of various line segments that are created if two ray (geometry), rays w ...
.
Computation of binary digits
In 1998 Simon Plouffe gave a ruler-and-compassalgorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algo ...
that can be used to compute binary digit
Binary may refer to:
Science and technology Mathematics
* Binary number, a representation of numbers using only two values (0 and 1) for each digit
* Binary function, a function that takes two arguments
* Binary operation, a mathematical o ...
s of certain numbers.
The algorithm involves the repeated doubling of an angle and becomes physically impractical after about 20 binary digits.
See also
*Carlyle circle
In mathematics, a Carlyle circle is a certain circle in a coordinate plane associated with a quadratic equation; it is named after Thomas Carlyle. The circle has the property that the equation solving, solutions of the quadratic equation are the ho ...
* Geometric cryptography
* Geometrography
*List of interactive geometry software
Interactive geometry software (IGS) or dynamic geometry environments (DGEs) are computer programs which allow one to create and then manipulate Geometry, geometric constructions, primarily in Euclidean plane geometry, plane geometry. In most IGS, o ...
, most of them show straightedge-and-compass constructions
* Mathematics of paper folding
*Underwood Dudley
Underwood Dudley (born January 6, 1937) is an American mathematician and writer. His popular works include several books describing crank mathematics by pseudomathematicians who incorrectly believe they have squared the circle or done other im ...
, a mathematician who has made a sideline of collecting false straightedge-and-compass proofs.
References
External links
Regular polygon constructions
by Dr. Math at ''The Math Forum @ Drexel''
Construction with the Compass Only
at ''
cut-the-knot
Alexander Bogomolny (January 4, 1948 July 7, 2018) was a Soviet Union, Soviet-born Israeli Americans, Israeli-American mathematician. He was Professor Emeritus of Mathematics at the University of Iowa, and formerly research fellow at the Moscow ...
''
Angle Trisection by Hippocrates
at ''cut-the-knot'' * {{Authority control Greek mathematics