Circular Path on:
[Wikipedia]
[Google]
[Amazon]
A circular arc is the arc of a
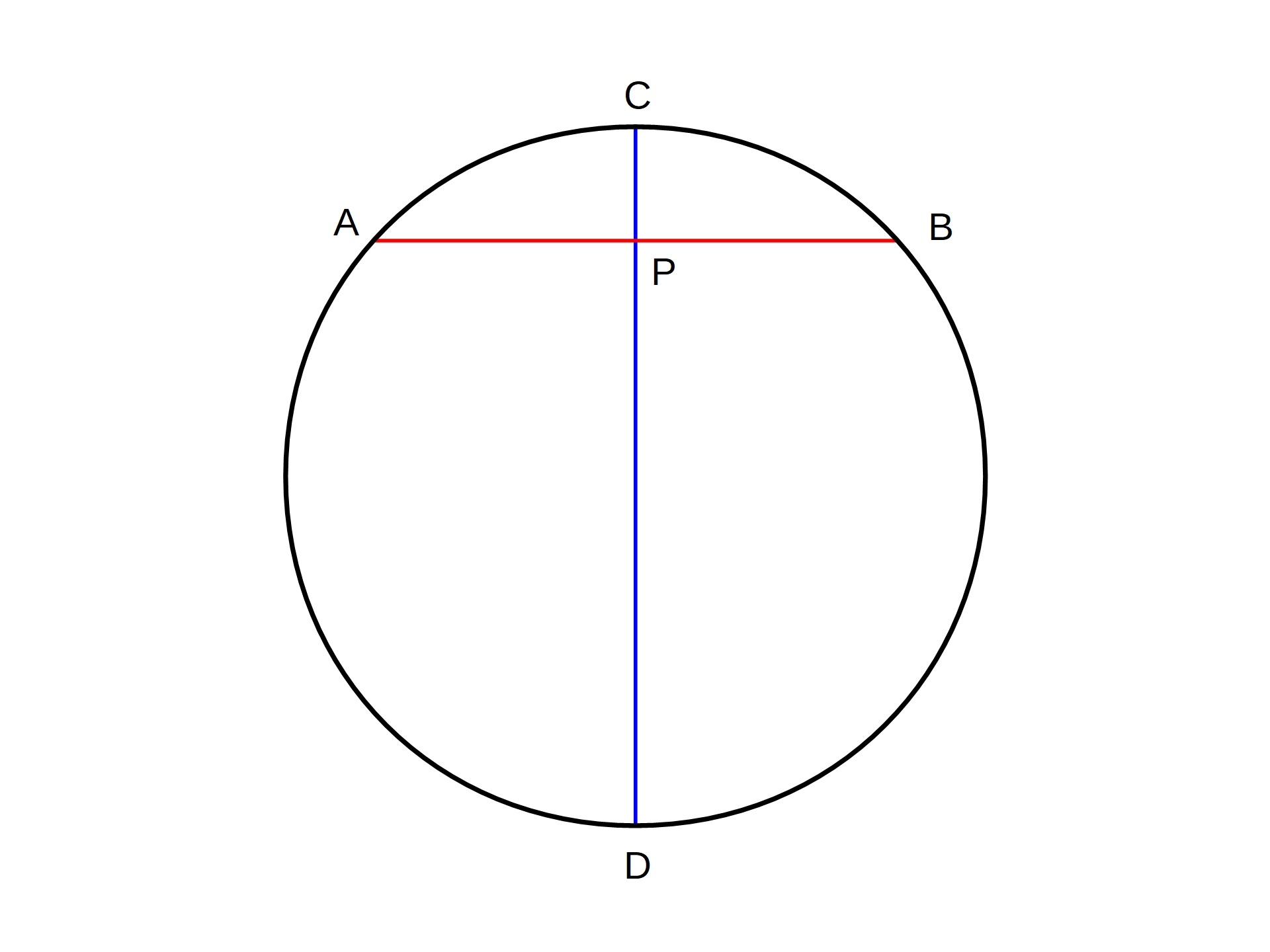 Using the intersecting chords theorem (also known as
Using the intersecting chords theorem (also known as
Table of contents for Math Open Reference Circle pages
With interactive animation
With interactive animation *{{MathWorld , urlname=Arc , title=Arc Circles Curves
circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
between a pair of distinct points
A point is a small dot or the sharp tip of something. Point or points may refer to:
Mathematics
* Point (geometry), an entity that has a location in space or on a plane, but has no extent; more generally, an element of some abstract topologica ...
. If the two points are not directly opposite each other, one of these arcs, the minor arc, subtends an angle at the center of the circle that is less than radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at ...
s (180 degrees); and the other arc, the major arc, subtends an angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
greater than radians. The arc of a circle is defined as the part or segment of the circumference
In geometry, the circumference () is the perimeter of a circle or ellipse. The circumference is the arc length of the circle, as if it were opened up and straightened out to a line segment. More generally, the perimeter is the curve length arou ...
of a circle. A straight line that connects the two ends of the arc is known as a '' chord'' of a circle. If the length
Length is a measure of distance. In the International System of Quantities, length is a quantity with Dimension (physical quantity), dimension distance. In most systems of measurement a Base unit (measurement), base unit for length is chosen, ...
of an arc is exactly half of the circle, it is known as a '' semicircular arc''.
Length
The length (more precisely,arc length
Arc length is the distance between two points along a section of a curve. Development of a formulation of arc length suitable for applications to mathematics and the sciences is a problem in vector calculus and in differential geometry. In the ...
) of an arc of a circle with radius ''r'' and subtending an angle ''θ'' (measured in radians) with the circle center — i.e., the central angle
A central angle is an angle whose apex (vertex) is the center O of a circle and whose legs (sides) are radii intersecting the circle in two distinct points A and B. Central angles are subtended by an arc between those two points, and the arc l ...
— is
:
This is because
:
Substituting in the circumference
:
and, with ''α'' being the same angle measured in degrees, since ''θ'' = , the arc length equals
:
A practical way to determine the length of an arc in a circle is to plot two lines from the arc's endpoints to the center of the circle, measure the angle where the two lines meet the center, then solve for L by cross-multiplying the statement:
:measure of angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
in degrees/360° = ''L''/circumference.
For example, if the measure of the angle is 60 degrees and the circumference is 24 inches, then
:
This is so because the circumference of a circle and the degrees of a circle, of which there are always 360, are directly proportional.
The upper half of a circle can be parameterized as
:
Then the arc length from to is
:
Sector area
The area of the sector formed by an arc and the center of a circle (bounded by the arc and the two radii drawn to its endpoints) is : The area ''A'' has the same proportion to thecircle area
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting ...
as the angle ''θ'' to a full circle:
:
We can cancel on both sides:
:
By multiplying both sides by ''r'', we get the final result:
:
Using the conversion described above, we find that the area of the sector for a central angle measured in degrees is
:
Segment area
The area of the shape bounded by the arc and the straight line between its two end points is : To get the area of the arc segment, we need to subtract the area of the triangle, determined by the circle's center and the two end points of the arc, from the area . SeeCircular segment
In geometry, a circular segment or disk segment (symbol: ) is a region of a disk which is "cut off" from the rest of the disk by a straight line. The complete line is known as a '' secant'', and the section inside the disk as a '' chord''.
More ...
for details.
Radius
 Using the intersecting chords theorem (also known as
Using the intersecting chords theorem (also known as power of a point
In elementary plane geometry, the power of a point is a real number that reflects the relative distance of a given point from a given circle. It was introduced by Jakob Steiner in 1826.
Specifically, the power \Pi(P) of a point P with respect to ...
or secant tangent theorem) it is possible to calculate the radius ''r'' of a circle given the height ''H'' and the width ''W'' of an arc:
Consider the chord with the same endpoints as the arc. Its perpendicular bisector is another chord, which is a diameter of the circle. The length of the first chord is ''W'', and it is divided by the bisector into two equal halves, each with length . The total length of the diameter is 2''r'', and it is divided into two parts by the first chord. The length of one part is the sagitta
Sagitta is a dim but distinctive constellation in the northern sky. Its name is Latin for 'arrow', not to be confused with the significantly larger constellation Sagittarius 'the archer'. It was included among the 48 constellations listed by t ...
of the arc, ''H'', and the other part is the remainder of the diameter, with length 2''r'' − ''H''. Applying the intersecting chords theorem to these two chords produces
:
whence
:
so
:
The arc, chord, and sagitta derive their names respectively from the Latin words for bow, bowstring, and arrow.
See also
*Biarc
A biarc is a smooth curve formed from two circular arcs. In order to make the biarc smooth (Geometric continuity, ''G''1 continuous), the two arcs should have the same tangent at the connecting point where they meet.
Biarcs are commonly used in ge ...
*Circle of a sphere
In spherical geometry, a spherical circle (often shortened to circle) is the locus of points on a sphere at constant spherical distance (the ''spherical radius'') from a given point on the sphere (the ''pole'' or ''spherical center''). It is ...
*Circular-arc graph
In graph theory, a circular-arc graph is the intersection graph of a set of arcs on the circle. It has one vertex for each arc in the set, and an edge between every pair of vertices corresponding to arcs that intersect.
Formally, let
:I_1, I ...
*Circular interpolation
Circular may refer to:
* The shape of a circle
* ''Circular'' (album), a 2006 album by Spanish singer Vega
* Circular letter (disambiguation), a document addressed to many destinations
** Government circular, a written statement of government pol ...
*Lemon (geometry)
In geometry, a lemon is a geometric shape that is constructed as the surface of revolution of a circular arc of angle less than half of a full circle rotated about an axis passing through the endpoints of the lens (or arc). The surface of revolut ...
*Meridian arc
In geodesy and navigation, a meridian arc is the curve (geometry), curve between two points near the Earth's surface having the same longitude. The term may refer either to a arc (geometry), segment of the meridian (geography), meridian, or to its ...
*Circumference
In geometry, the circumference () is the perimeter of a circle or ellipse. The circumference is the arc length of the circle, as if it were opened up and straightened out to a line segment. More generally, the perimeter is the curve length arou ...
*Circular motion
In physics, circular motion is movement of an object along the circumference of a circle or rotation along a circular arc. It can be uniform, with a constant rate of rotation and constant tangential speed, or non-uniform with a changing rate ...
*Tangential speed
Tangential speed is the speed of an object undergoing circular motion, i.e., moving along a circular path. A point on the outside edge of a merry-go-round or turntable travels a greater distance in one complete rotation than a point nearer the c ...
External links
Table of contents for Math Open Reference Circle pages
With interactive animation
With interactive animation *{{MathWorld , urlname=Arc , title=Arc Circles Curves