|
Circular Path
A circular arc is the arc (geometry), arc of a circle between a pair of distinct Point (geometry), points. If the two points are not directly opposite each other, one of these arcs, the minor arc, subtended angle, subtends an angle at the center of the circle that is less than Pi, radians (180 Degree (angle), degrees); and the other arc, the major arc, subtends an angle greater than radians. The arc of a circle is defined as the part or segment of the circumference of a circle. A straight line that connects the two ends of the arc is known as a ''chord (geometry), chord'' of a circle. If the length of an arc is exactly half of the circle, it is known as a ''semicircle, semicircular arc''. Length The length (more precisely, arc length) of an arc of a circle with radius ''r'' and subtending an angle ''θ'' (measured in radians) with the circle center — i.e., the central angle — is : L = \theta r. This is because :\frac=\frac. Substituting in the circumference :\frac=\fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle Arc
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
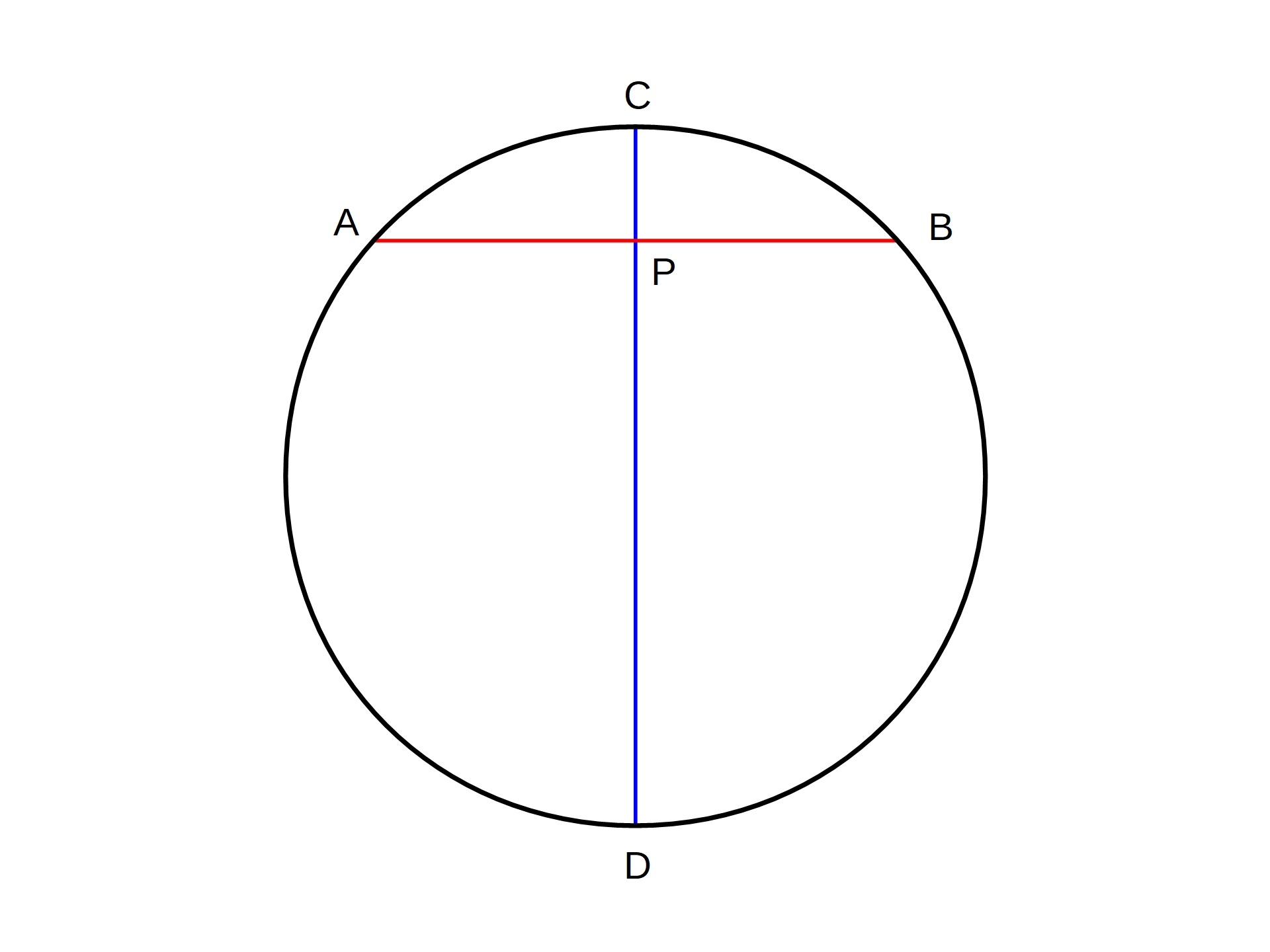
Power Of A Point
In elementary plane geometry, the power of a point is a real number that reflects the relative distance of a given point from a given circle. It was introduced by Jakob Steiner in 1826. Specifically, the power \Pi(P) of a point P with respect to a circle c with center O and radius r is defined by : \Pi(P)=, PO, ^2 - r^2. If P is ''outside'' the circle, then \Pi(P)>0, if P is ''on'' the circle, then \Pi(P)=0 and if P is ''inside'' the circle, then \Pi(P)<0. Due to the Pythagorean theorem the number has the simple geometric meanings shown in the diagram: For a point outside the circle is the squared tangential distance of point to the circle . Points with equal power, isolines of , are circles concentric to circle . Steiner used the power of a point for proofs of several statements on circles, for example: * Determination of a circle, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangential Speed
Tangential speed is the speed of an object undergoing circular motion, i.e., moving along a circular path. A point on the outside edge of a merry-go-round or turntable travels a greater distance in one complete rotation than a point nearer the center. Travelling a greater distance in the same time means a greater speed, and so linear speed is greater on the outer edge of a rotating object than it is closer to the axis. This speed along a circular path is known as ''tangential speed'' because the direction of motion is tangent to the circumference of the circle. For circular motion, the terms linear speed and tangential speed are used interchangeably, and is measured in SI units as meters per second (m/s). Formula Rotational speed (or rotational frequency) measures the number of revolutions per unit of time. All parts of a rigid merry-go-round or turntable turn about the axis of rotation in the same amount of time. Thus, all parts share the same rate of rotation, or the same numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular Motion
In physics, circular motion is movement of an object along the circumference of a circle or rotation along a circular arc. It can be uniform, with a constant rate of rotation and constant tangential speed, or non-uniform with a changing rate of rotation. The rotation around a fixed axis of a three-dimensional body involves the circular motion of its parts. The equations of motion describe the movement of the center of mass of a body, which remains at a constant distance from the axis of rotation. In circular motion, the distance between the body and a fixed point on its surface remains the same, i.e., the body is assumed rigid. Examples of circular motion include: special satellite orbits around the Earth (circular orbits), a ceiling fan's blades rotating around a hub, a stone that is tied to a rope and is being swung in circles, a car turning through a curve in a race track, an electron moving perpendicular to a uniform magnetic field, and a gear turning inside a mechani ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circumference
In geometry, the circumference () is the perimeter of a circle or ellipse. The circumference is the arc length of the circle, as if it were opened up and straightened out to a line segment. More generally, the perimeter is the curve length around any closed figure. Circumference may also refer to the circle itself, that is, the Locus (geometry), locus corresponding to the Edge (geometry), edge of a Disk (geometry), disk. The is the circumference, or length, of any one of its great circles. Circle The circumference of a circle is the distance around it, but if, as in many elementary treatments, distance is defined in terms of straight lines, this cannot be used as a definition. Under these circumstances, the circumference of a circle may be defined as the Limit (mathematics), limit of the perimeters of inscribed regular polygons as the number of sides increases without bound. The term circumference is used when measuring physical objects, as well as when considering abstrac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meridian Arc
In geodesy and navigation, a meridian arc is the curve (geometry), curve between two points near the Earth's surface having the same longitude. The term may refer either to a arc (geometry), segment of the meridian (geography), meridian, or to its Arc length, length. Both the practical determination of meridian arcs (employing measuring instruments in field campaigns) as well as its theoretical calculation (based on geometry and abstract mathematics) have been pursued for many years. Measurement The purpose of measuring meridian arcs is to determine a figure of the Earth. One or more measurements of meridian arcs can be used to infer the shape of the reference ellipsoid that best approximates the geoid in the region of the measurements. Measurements of meridian arcs at several latitudes along many meridians around the world can be combined in order to approximate a ''geocentric ellipsoid'' intended to fit the entire world. The earliest determinations of the size of a spherical E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lemon (geometry)
In geometry, a lemon is a geometric shape that is constructed as the surface of revolution of a circular arc of angle less than half of a full circle rotated about an axis passing through the endpoints of the lens (or arc). The surface of revolution of the complementary arc of the same circle, through the same axis, is called an apple. The apple and lemon together make up a spindle torus (or ''self-crossing torus'' or ''self-intersecting torus''). The lemon forms the boundary of a convex set, while its surrounding apple is non-convex. The ball in North American football has a shape resembling a geometric lemon. However, although used with a related meaning in geometry, the term "football" is more commonly used to refer to a surface of revolution whose Gaussian curvature is positive and constant, formed from a more complicated curve than a circular arc. Alternatively, a football may refer to a more abstract orbifold, a surface modeled locally on a sphere except at two points. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular Interpolation
*
{{disambiguation ...
Circular may refer to: * The shape of a circle * ''Circular'' (album), a 2006 album by Spanish singer Vega * Circular letter (other), a document addressed to many destinations ** Government circular, a written statement of government policy **Circulaire * Circular reasoning, a type of logical fallacy * Circular reference *Circular Quay, Australia *Circular Park, Armenia See also * Circular DNA (other) * Circular Line (other) * Circularity (other) Circularity may refer to: *Circular definition *Circular economy *Circular reasoning Circular reasoning (, "circle in proving"; also known as circular logic) is a fallacy, logical fallacy in which the reasoner begins with what they are trying ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular-arc Graph
In graph theory, a circular-arc graph is the intersection graph of a set of arcs on the circle. It has one vertex for each arc in the set, and an edge between every pair of vertices corresponding to arcs that intersect. Formally, let :I_1, I_2, \ldots, I_n \subset C_1 be a set of arcs. Then the corresponding circular-arc graph is ''G'' = (''V'', ''E'') where : V = \ and : \ \in E \iff I_\alpha \cap I_\beta \neq \varnothing. A family of arcs that corresponds to G is called an ''arc model''. Recognition demonstrated the first polynomial recognition algorithm for circular-arc graphs, which runs in (n^3) time. gave the first linear ((n+m)) time recognition algorithm, where m is the number of edges. More recently, Kaplan and Nussbaum developed a simpler linear time recognition algorithm. Relation to other graph classes Circular-arc graphs are a natural generalization of interval graphs. If a circular-arc graph ''G'' has an arc model that leaves some point of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle Of A Sphere
In spherical geometry, a spherical circle (often shortened to circle) is the locus of points on a sphere at constant spherical distance (the ''spherical radius'') from a given point on the sphere (the ''pole'' or ''spherical center''). It is a curve of constant geodesic curvature relative to the sphere, analogous to a line or circle in the Euclidean plane; the curves analogous to straight lines are called ''great circles'', and the curves analogous to planar circles are called small circles or lesser circles. If the sphere is embedded in three-dimensional Euclidean space, its circles are the intersections of the sphere with planes, and the great circles are intersections with planes passing through the center of the sphere. Fundamental concepts Intrinsic characterization A spherical circle with zero geodesic curvature is called a ''great circle'', and is a geodesic analogous to a straight line in the plane. A great circle separates the sphere into two equal '' hem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biarc
A biarc is a smooth curve formed from two circular arcs. In order to make the biarc smooth (Geometric continuity, ''G''1 continuous), the two arcs should have the same tangent at the connecting point where they meet. Biarcs are commonly used in geometric modeling and computer graphics. They can be used to approximation, approximate Spline (mathematics), splines and other curve, plane curves by placing the two outer endpoints of the biarc along the curve to be approximated, with a tangent that matches the curve, and then choosing a middle point that best fits the curve. This choice of three points and two tangents determines a unique pair of circular arcs, and the Locus (mathematics), locus of middle points for which these two arcs form a biarc is itself a circular arc. In particular, to approximate a Bézier curve in this way, the middle point of the biarc should be chosen as the incenter of the triangle formed by the two endpoints of the Bézier curve and the point where their two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bow (weapon)
The bow and arrow is a ranged weapon system consisting of an elastic launching device (bow) and long-shafted projectiles (arrows). Humans used bows and arrows for hunting and aggression long before recorded history, and the practice was common to many prehistoric cultures. They were important weapons of war from ancient history until the early modern period, when they were rendered increasingly obsolete by the development of the more powerful and accurate firearms. Today, bows and arrows are mostly used for hunting and sports. Archery is the art, practice, or skill of using bows to shoot arrows.Paterson ''Encyclopaedia of Archery'' p. 17 A person who shoots arrows with a bow is called a bowman or an archer. Someone who makes bows is known as a bowyer,Paterson ''Encyclopaedia of Archery'' p. 31 someone who makes arrows is a fletcher,Paterson ''Encyclopaedia of Archery'' p. 56 and someone who manufactures metal arrowheads is an arrowsmith.Paterson ''Encyclopaedia of Archery'' p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |