|
Biarc
A biarc is a smooth curve formed from two circular arcs. In order to make the biarc smooth ( ''G''1 continuous), the two arcs should have the same tangent at the connecting point where they meet. Biarcs are commonly used in geometric modeling and computer graphics. They can be used to approximate splines and other plane curves by placing the two outer endpoints of the biarc along the curve to be approximated, with a tangent that matches the curve, and then choosing a middle point that best fits the curve. This choice of three points and two tangents determines a unique pair of circular arcs, and the locus of middle points for which these two arcs form a biarc is itself a circular arc. In particular, to approximate a Bézier curve A Bézier curve ( ) is a parametric curve used in computer graphics and related fields. A set of discrete "control points" defines a smooth, continuous curve by means of a formula. Usually the curve is intended to approximate a real-world shape t ... ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bézier Curve
A Bézier curve ( ) is a parametric curve used in computer graphics and related fields. A set of discrete "control points" defines a smooth, continuous curve by means of a formula. Usually the curve is intended to approximate a real-world shape that otherwise has no mathematical representation or whose representation is unknown or too complicated. The Bézier curve is named after French engineer Pierre Bézier (1910–1999), who used it in the 1960s for designing curves for the bodywork of Renault cars. Other uses include the design of computer fonts and animation. Bézier curves can be combined to form a Bézier spline, or generalized to higher dimensions to form Bézier surfaces. The Bézier triangle is a special case of the latter. In vector graphics, Bézier curves are used to model smooth curves that can be scaled indefinitely. "Paths", as they are commonly referred to in image manipulation programs, are combinations of linked Bézier curves. Paths are not bound by the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
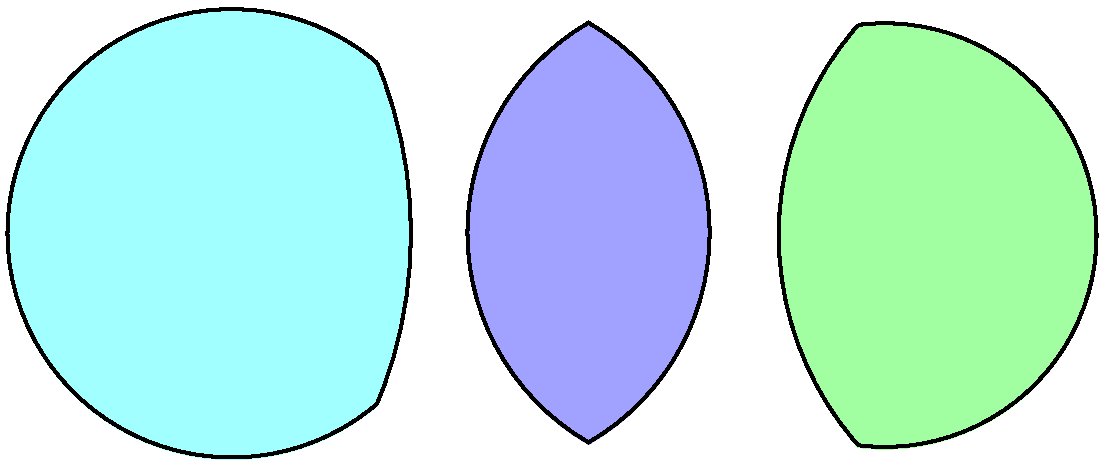
Lune (geometry)
In plane geometry, a lune () is the concave-convex region bounded by two circular arcs. It has one boundary portion for which the connecting segment of any two nearby points moves outside the region and another boundary portion for which the connecting segment of any two nearby points lies entirely inside the region. A convex-convex region is termed a lens. Formally, a lune is the relative complement of one disk in another (where they intersect but neither is a subset of the other). Alternatively, if A and B are disks, then A \smallsetminus A \cap B is a lune. Squaring the lune In the 5th century BC, Hippocrates of Chios showed that the Lune of Hippocrates and two other lunes could be exactly squared (converted into a square having the same area) by straightedge and compass. In 1766 the Finnish mathematician Daniel Wijnquist, quoting Daniel Bernoulli Daniel Bernoulli FRS (; – 27 March 1782) was a Swiss mathematician and physicist and was one of the many promi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lens (geometry)
In 2-dimensional geometry, a lens is a convex region bounded by two circular arcs joined to each other at their endpoints. In order for this shape to be convex, both arcs must bow outwards (convex-convex). This shape can be formed as the intersection of two circular disks. It can also be formed as the union of two circular segments (regions between the chord of a circle and the circle itself), joined along a common chord. Types If the two arcs of a lens have equal radius, it is called a symmetric lens, otherwise is an asymmetric lens. The vesica piscis is one form of a symmetric lens, formed by arcs of two circles whose centers each lie on the opposite arc. The arcs meet at angles of 120° at their endpoints. Area ;Symmetric The area of a symmetric lens can be expressed in terms of the radius ''R'' and arc lengths ''θ'' in radians: :A = R^2\left(\theta - \sin \theta \right). ;Asymmetric The area of an asymmetric lens formed from circles of radii ''R'' and ''r'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incenter
In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle. Together with the centroid, circumcenter, and orthocenter, it is one of the four triangle centers known to the ancient Greeks, and the only one of the four that does not in general lie on the Euler line. It is the first listed center, X(1), in Clark Kimberling's Encyclopedia of Triangle Centers, and the identity element of the multiplicative group of triangle centers.. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Locus (mathematics)
In geometry, a locus (plural: ''loci'') (Latin word for "place", "location") is a set of all points (commonly, a line, a line segment, a curve or a surface), whose location satisfies or is determined by one or more specified conditions.. In other words, the set of the points that satisfy some property is often called the ''locus of a point'' satisfying this property. The use of the singular in this formulation is a witness that, until the end of the 19th century, mathematicians did not consider infinite sets. Instead of viewing lines and curves as sets of points, they viewed them as places where a point may be ''located'' or may move. History and philosophy Until the beginning of the 20th century, a geometrical shape (for example a curve) was not considered as an infinite set of points; rather, it was considered as an entity on which a point may be located or on which it moves. Thus a circle in the Euclidean plane was defined as the ''locus'' of a point that is at a given dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Smooth Curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that appeared more than 2000 years ago in Euclid's ''Elements'': "The urvedline is ��the first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which ��will leave from its imaginary moving some vestige in length, exempt of any width." This definition of a curve has been formalized in modern mathematics as: ''A curve is the image of an interval to a topological space by a continuous function''. In some contexts, the function that defines the curve is called a ''parametrization'', and the curve is a parametric curve. In this article, these curves are sometimes called ''topological curves'' to distinguish them from more constrained curves suc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |