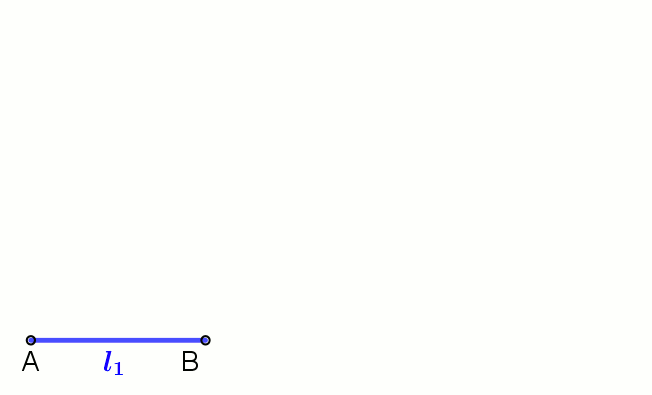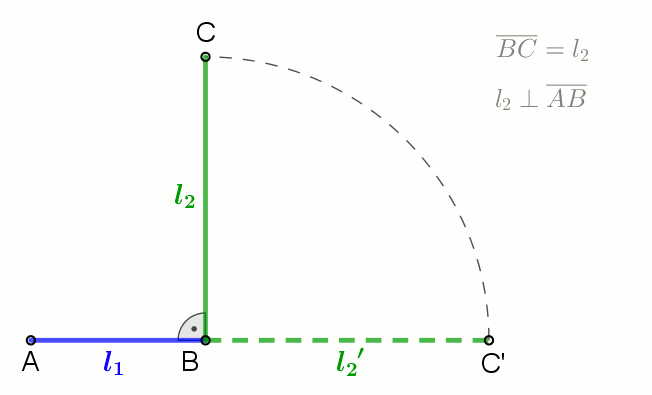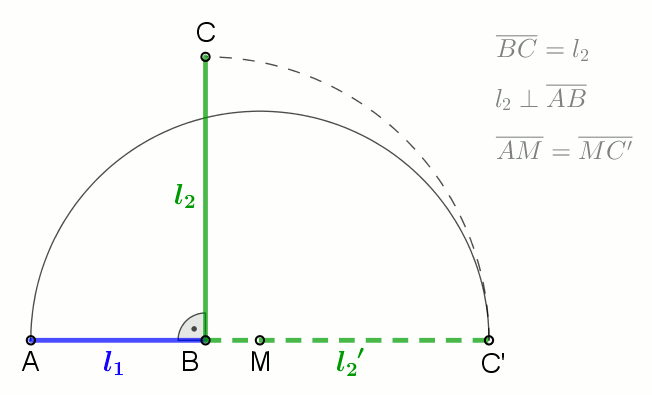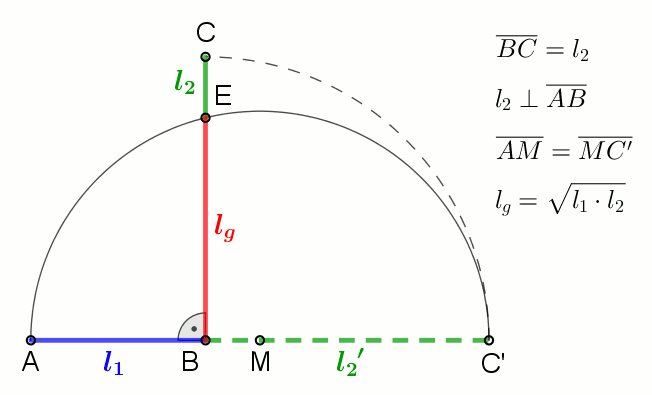|
Semicircle
In mathematics (and more specifically geometry), a semicircle is a one-dimensional locus of points that forms half of a circle. The full arc of a semicircle always measures 180° (equivalently, radians, or a half-turn). It has only one line of symmetry (reflection symmetry). In non-technical usage, the term "semicircle" is sometimes used to refer to a half- disk, which is a two-dimensional geometric shape that also includes the diameter segment from one end of the arc to the other as well as all the interior points. By Thales' theorem, any triangle inscribed in a semicircle with a vertex at each of the endpoints of the semicircle and the third vertex elsewhere on the semicircle is a right triangle, with a right angle at the third vertex. All lines intersecting the semicircle perpendicularly are concurrent at the center of the circle containing the given semicircle. Uses A semicircle can be used to construct the arithmetic and geometric means of two lengths using str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the centre is called the radius. Usually, the radius is required to be a positive number. A circle with r=0 (a single point) is a degenerate case. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted. Specifically, a circle is a simple closed curve that divides the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is only the boundary and the whole figure is called a '' disc''. A circle may also be defined as a special ki ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perpendicular
In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle (90 degrees or π/2 radians). The condition of perpendicularity may be represented graphically using the ''perpendicular symbol'', ⟂. It can be defined between two lines (or two line segments), between a line and a plane, and between two planes. Perpendicularity is one particular instance of the more general mathematical concept of ''orthogonality''; perpendicularity is the orthogonality of classical geometric objects. Thus, in advanced mathematics, the word "perpendicular" is sometimes used to describe much more complicated geometric orthogonality conditions, such as that between a surface and its '' normal vector''. Definitions A line is said to be perpendicular to another line if the two lines intersect at a right angle. Explicitly, a first line is perpendicular to a second line if (1) the two lines meet; and (2) at the point of intersection the straight angle on one side ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Straight Line
In geometry, a line is an infinitely long object with no width, depth, or curvature. Thus, lines are one-dimensional objects, though they may exist in two, three, or higher dimension spaces. The word ''line'' may also refer to a line segment in everyday life, which has two points to denote its ends. Lines can be referred by two points that lay on it (e.g., \overleftrightarrow) or by a single letter (e.g., \ell). Euclid described a line as "breadthless length" which "lies evenly with respect to the points on itself"; he introduced several postulates as basic unprovable properties from which he constructed all of geometry, which is now called Euclidean geometry to avoid confusion with other geometries which have been introduced since the end of the 19th century (such as non-Euclidean, projective and affine geometry). In modern mathematics, given the multitude of geometries, the concept of a line is closely tied to the way the geometry is described. For instance, in analytic ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane (geometry)
In mathematics, a plane is a Euclidean ( flat), two- dimensional surface that extends indefinitely. A plane is the two-dimensional analogue of a point (zero dimensions), a line (one dimension) and three-dimensional space. Planes can arise as subspaces of some higher-dimensional space, as with one of a room's walls, infinitely extended, or they may enjoy an independent existence in their own right, as in the setting of two-dimensional Euclidean geometry. Sometimes the word ''plane'' is used more generally to describe a two-dimensional surface, for example the hyperbolic plane and elliptic plane. When working exclusively in two-dimensional Euclidean space, the definite article is used, so ''the'' plane refers to the whole space. Many fundamental tasks in mathematics, geometry, trigonometry, graph theory, and graphing are performed in a two-dimensional space, often in the plane. Euclidean geometry Euclid set forth the first great landmark of mathematical thought, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arbelos
In geometry, an arbelos is a plane region bounded by three semicircles with three apexes such that each corner of each semicircle is shared with one of the others (connected), all on the same side of a straight line (the ''baseline'') that contains their diameters. The earliest known reference to this figure is in Archimedes's ''Book of Lemmas'', where some of its mathematical properties are stated as Propositions 4 through 8. The word ''arbelos'' is Greek for 'shoemaker's knife'. The figure is closely related to the Pappus chain. Properties Two of the semicircles are necessarily concave, with arbitrary diameters and ; the third semicircle is convex, with diameter Area The area of the arbelos is equal to the area of a circle with diameter . Proof: For the proof, reflect the arbelos over the line through the points and , and observe that twice the area of the arbelos is what remains when the areas of the two smaller circles (with diameters , ) are subtracted from the area ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arbelos
In geometry, an arbelos is a plane region bounded by three semicircles with three apexes such that each corner of each semicircle is shared with one of the others (connected), all on the same side of a straight line (the ''baseline'') that contains their diameters. The earliest known reference to this figure is in Archimedes's ''Book of Lemmas'', where some of its mathematical properties are stated as Propositions 4 through 8. The word ''arbelos'' is Greek for 'shoemaker's knife'. The figure is closely related to the Pappus chain. Properties Two of the semicircles are necessarily concave, with arbitrary diameters and ; the third semicircle is convex, with diameter Area The area of the arbelos is equal to the area of a circle with diameter . Proof: For the proof, reflect the arbelos over the line through the points and , and observe that twice the area of the arbelos is what remains when the areas of the two smaller circles (with diameters , ) are subtracted from the area ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lemma (mathematics)
In mathematics, informal logic and argument mapping, a lemma (plural lemmas or lemmata) is a generally minor, proven proposition which is used as a stepping stone to a larger result. For that reason, it is also known as a "helping theorem" or an "auxiliary theorem". In many cases, a lemma derives its importance from the theorem it aims to prove; however, a lemma can also turn out to be more important than originally thought. The word "lemma" derives from the Ancient Greek ("anything which is received", such as a gift, profit, or a bribe). Comparison with theorem There is no formal distinction between a lemma and a theorem, only one of intention (see Theorem terminology). However, a lemma can be considered a minor result whose sole purpose is to help prove a more substantial theorem – a step in the direction of proof. Well-known lemmas A good stepping stone can lead to many others. Some powerful results in mathematics are known as lemmas, first named for their originally mi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadrature (mathematics)
In mathematics, quadrature is a historical term which means the process of determining area. This term is still used nowadays in the context of differential equations, where "solving an equation by quadrature" or "reduction to quadrature" means expressing its solution in terms of integrals. Quadrature problems served as one of the main sources of problems in the development of calculus, and introduce important topics in mathematical analysis. History Antiquity Greek mathematicians understood the determination of an area of a figure as the process of geometrically constructing a square having the same area (''squaring''), thus the name ''quadrature'' for this process. The Greek geometers were not always successful (see squaring the circle), but they did carry out quadratures of some figures whose sides were not simply line segments, such as the lune of Hippocrates and the parabola. By a certain Greek tradition, these constructions had to be performed using only a compass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides ''a'', ''b'' and the hypotenuse ''c'', often called the Pythagorean equation: :a^2 + b^2 = c^2 , The theorem is named for the Greek philosopher Pythagoras, born around 570 BC. The theorem has been proven numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years. When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies the Pythagorean relation: the squared ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radius
In classical geometry, a radius ( : radii) of a circle or sphere is any of the line segments from its center to its perimeter, and in more modern usage, it is also their length. The name comes from the latin ''radius'', meaning ray but also the spoke of a chariot wheel. as a function of axial position ../nowiki>" Spherical coordinates In a spherical coordinate system, the radius describes the distance of a point from a fixed origin. Its position if further defined by the polar angle measured between the radial direction and a fixed zenith direction, and the azimuth angle, the angle between the orthogonal projection of the radial direction on a reference plane that passes through the origin and is orthogonal to the zenith, and a fixed reference direction in that plane. See also *Bend radius *Filling radius in Riemannian geometry *Radius of convergence * Radius of convexity *Radius of curvature *Radius of gyration ''Radius of gyration'' or gyradius of a body about the axis of r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Mean
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a set of numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean is defined as the th root of the product of numbers, i.e., for a set of numbers , the geometric mean is defined as :\left(\prod_^n a_i\right)^\frac = \sqrt /math> or, equivalently, as the arithmetic mean in logscale: :\exp For instance, the geometric mean of two numbers, say 2 and 8, is just the square root of their product, that is, \sqrt = 4. As another example, the geometric mean of the three numbers 4, 1, and 1/32 is the cube root of their product (1/8), which is 1/2, that is, \sqrt = 1/2. The geometric mean applies only to positive numbers. The geometric mean is often used for a set of numbers whose values are meant to be multiplied together or are exponential in nature, such as a set of growth figures: values of the human population or int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
