Antiderivatives

In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function is a differentiable function whose derivative is equal to the original function . This can be stated symbolically as . The process of solving for antiderivatives is called antidifferentiation (or indefinite integration), and its opposite operation is called ''differentiation'', which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as and .

Antiderivatives are related to definite integrals through the second fundamental theorem of calculus: the definite integral of a function over a closed interval where the function is Riemann integrable is equal to the difference between the values of an antiderivative evaluated at the endpoints of the interval.

In physics, antiderivatives arise in the context of rectilinear motion (e.g., in explaining the relationship between position, velocity and acceleration). The discrete equivalent of the notion of antiderivative is antidifference.

Examples

The function $F(x) = \tfrac$ is an antiderivative of $f(x) = x^2$, since the derivative of $\tfrac$ is $x^2$, and since the derivative of a constant is zero, $x^2$ will have an infinite number of antiderivatives, such as $\tfrac, \tfrac+1, \tfrac-2$, etc. Thus, all the antiderivatives of $x^2$ can be obtained by changing the value of in $F(x) = \tfrac+c$, where is an arbitrary constant known as the constant of integration. 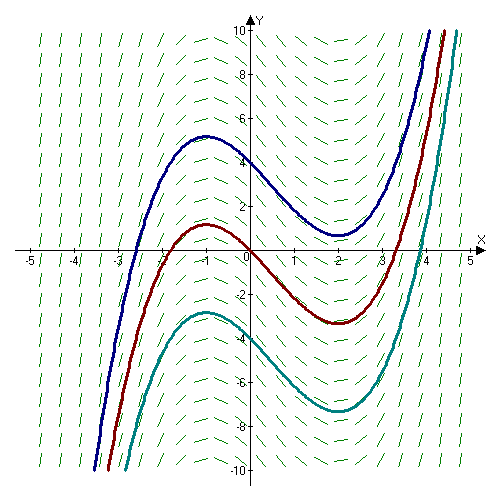Essentially, the graphs of antiderivatives of a given function are vertical translations of each other, with each graph's vertical location depending upon the value .

More generally, the power function $f(x) = x^n$ has antiderivative $F(x) = \tfrac + c$ if , and $F(x) = \ln , x, + c$ if .

In physics, the integration of acceleration yields velocity plus a constant. The constant is the initial velocity term that would be lost upon taking the derivative of velocity, because the derivative of a constant term is zero. This same pattern applies to further integrations and derivatives of motion (position, velocity, acceleration, and so on). Thus, integration produces the relations of acceleration, velocity and displacement:
:$\int a\ \mathrmt = v + C$
:$\int v\ \mathrmt = d + C$

Uses and properties

Antiderivatives can be used to compute definite integrals, using the fundamental theorem of calculus: if is an antiderivative of the integrable function over the interval ,b/math>, then:

:$\int_a^b f(x)\,\mathrmx = F(b) - F(a).$

Because of this, each of the infinitely many antiderivatives of a given function may be called the "indefinite integral" of ''f'' and written using the integral symbol with no bounds:
:$\int f(x)\,\mathrmx.$

If is an antiderivative of , and the function is defined on some interval, then every other antiderivative of differs from by a constant: there exists a number such that $G(x) = F(x)+c$ for all . is called the constant of integration. If the domain of is a disjoint union of two or more (open) intervals, then a different constant of integration may be chosen for each of the intervals. For instance

:$F(x)=\begin-\frac+c_1\quad x<0\\-\frac+c_2\quad x>0\end$

is the most general antiderivative of $f(x)=1/x^2$ on its natural domain $(-\infty,0)\cup(0,\infty).$

Every continuous function has an antiderivative, and one antiderivative is given by the definite integral of with variable upper boundary:
:$F(x)=\int_0^x f(t)\,\mathrmt.$
Varying the lower boundary produces other antiderivatives (but not necessarily all possible antiderivatives). This is another formulation of the fundamental theorem of calculus.

There are many functions whose antiderivatives, even though they exist, cannot be expressed in terms of elementary functions (like polynomials, exponential functions, logarithms, trigonometric functions, inverse trigonometric functions and their combinations). Examples of these are
:$\int e^\,\mathrmx,\qquad \int \sin x^2\,\mathrmx, \qquad\int \frac\,\mathrmx,\qquad \int\frac\,\mathrmx,\qquad \int x^\,\mathrmx.$
''From left to right, the functions are the error function, the Fresnel function, the sine integral, the logarithmic integral function and sophomore's dream.'' For a more detailed discussion, see also Differential Galois theory.

Techniques of integration

Finding antiderivatives of elementary functions is often considerably harder than finding their derivatives (indeed, there is no pre-defined method for computing indefinite integrals). For some elementary functions, it is impossible to find an antiderivative in terms of other elementary functions. To learn more, see elementary functions and nonelementary integral.

There exist many properties and techniques for finding antiderivatives. These include, among others:

* The linearity of integration (which breaks complicated integrals into simpler ones)
* Integration by substitution, often combined with trigonometric identities or the natural logarithm
* The inverse chain rule method (a special case of integration by substitution)
* Integration by parts (to integrate products of functions)
* Inverse function integration (a formula that expresses the antiderivative of the inverse of an invertible and continuous function , in terms of the antiderivative of and of ).
* The method of partial fractions in integration (which allows us to integrate all rational functions—fractions of two polynomials)
* The Risch algorithm
* Additional techniques for multiple integrations (see for instance double integrals, polar coordinates, the Jacobian and the Stokes' theorem)
* Numerical integration (a technique for approximating a definite integral when no elementary antiderivative exists, as in the case of )
* Algebraic manipulation of integrand (so that other integration techniques, such as integration by substitution, may be used)
*Cauchy formula for repeated integration (to calculate the -times antiderivative of a function) $\int_^x \int_^ \cdots \int_^ f(x_n) \,\mathrmx_n \cdots \, \mathrmx_2\, \mathrmx_1 = \int_^x f(t) \frac\,\mathrmt.$

Computer algebra systems can be used to automate some or all of the work involved in the symbolic techniques above, which is particularly useful when the algebraic manipulations involved are very complex or lengthy. Integrals which have already been derived can be looked up in a table of integrals.

Of non-continuous functions

Non-continuous functions can have antiderivatives. While there are still open questions in this area, it is known that:
* Some highly pathological functions with large sets of discontinuities may nevertheless have antiderivatives.
* In some cases, the antiderivatives of such pathological functions may be found by Riemann integration, while in other cases these functions are not Riemann integrable.

Assuming that the domains of the functions are open intervals:

* A necessary, but not sufficient, condition for a function to have an antiderivative is that have the intermediate value property. That is, if is a subinterval of the domain of and is any real number between and , then there exists a between and such that . This is a consequence of Darboux's theorem.
* The set of discontinuities of must be a meagre set. This set must also be an F-sigma set (since the set of discontinuities of any function must be of this type). Moreover, for any meagre F-sigma set, one can construct some function having an antiderivative, which has the given set as its set of discontinuities.
* If has an antiderivative, is bounded on closed finite subintervals of the domain and has a set of discontinuities of Lebesgue measure 0, then an antiderivative may be found by integration in the sense of Lebesgue. In fact, using more powerful integrals like the Henstock–Kurzweil integral, every function for which an antiderivative exists is integrable, and its general integral coincides with its antiderivative.
* If has an antiderivative on a closed interval ,b/math>, then for any choice of partition a=x_0 if one chooses sample points x_i^*\in _,x_i/math> as specified by the mean value theorem, then the corresponding Riemann sum telescopes to the value $F(b)-F(a)$.
::$\begin \sum_^n f(x_i^*)(x_i-x_) & = \sum_^n$(x_i)-F(x_)\\
& = F(x_n)-F(x_0) = F(b)-F(a)
\end
:However if is unbounded, or if is bounded but the set of discontinuities of has positive Lebesgue measure, a different choice of sample points $x_i^*$ may give a significantly different value for the Riemann sum, no matter how fine the partition. See Example 4 below.

Some examples

Basic formulae

* If $f(x) = g(x)$, then $\int g(x) \mathrmx = f(x) + C$.

* $\int 1\ \mathrmx = x + C$
* $\int a\ \mathrmx = ax + C$
* $\int x^n \mathrmx = \frac + C;\ n \neq -1$
* $\int \sin\ \mathrmx = -\cos + C$
* $\int \cos\ \mathrmx = \sin + C$
* $\int \sec^2\ \mathrmx = \tan + C$
* $\int \csc^2\ \mathrmx = -\cot + C$
* $\int \sec\tan\ \mathrmx = \sec + C$
* $\int \csc\cot\ \mathrmx = -\csc + C$
* $\int \frac\ \mathrmx = \ln, x, + C$
* $\int e^ \mathrmx = e^ + C$
* $\int a^ \mathrmx = \frac + C;\ a > 0,\ a \neq 1$

See also

* Antiderivative (complex analysis)
* Formal antiderivative
* Jackson integral
* Lists of integrals
* Symbolic integration
* Area

Notes

References

Further reading

* ''Introduction to Classical Real Analysis'', by Karl R. Stromberg; Wadsworth, 1981 (se
also


''Historical Essay On Continuity Of Derivatives''
by Dave L. Renfro

External links

Wolfram Integrator
— Free online symbolic integration with Mathematica

Mathematical Assistant on Web
— symbolic computations online. Allows users to integrate in small steps (with hints for next step (integration by parts, substitution, partial fractions, application of formulas and others), powered by Maxima

Function Calculator
from WIMS


at HyperPhysics

Antiderivatives and indefinite integrals
at the Khan Academy

Integral calculator
at Symbolab

The Antiderivative
at MIT

Introduction to Integrals
at SparkNotes

Antiderivatives
at Harvy Mudd College

{{Authority control

Integral calculus
Linear operators in calculus