|
Henstock–Kurzweil Integral
In mathematics, the Henstock–Kurzweil integral or generalized Riemann integral or gauge integral – also known as the (narrow) Denjoy integral (pronounced ), Luzin integral or Perron integral, but not to be confused with the more general wide Denjoy integral – is one of a number of inequivalent definitions of the integral of a function. It is a generalization of the Riemann integral, and in some situations is more general than the Lebesgue integral. In particular, a function is Lebesgue integrable if and only if the function and its absolute value are Henstock–Kurzweil integrable. This integral was first defined by Arnaud Denjoy (1912). Denjoy was interested in a definition that would allow one to integrate functions like :f(x)=\frac\sin\left(\frac\right). This function has a singularity at 0, and is not Lebesgue integrable. However, it seems natural to calculate its integral except over the interval and then let . Trying to create a general theory, Denjoy used t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cousin's Theorem
In real analysis, a branch of mathematics, Cousin's theorem states that: :If for every point of a closed region (in modern terms, " closed and bounded") there is a circle of finite radius (in modern term, a " neighborhood"), then the region can be divided into a finite number of subregions such that each subregion is interior to a circle of a given set having its center in the subregion.Hildebrandt 1925, p. 29 This result was originally proved by Pierre Cousin, a student of Henri Poincaré, in 1895, and it extends the original Heine–Borel theorem on compactness for arbitrary covers of compact subsets of \mathbb^n. However, Pierre Cousin did not receive any credit. Cousin's theorem was generally attributed to Henri Lebesgue as the Borel–Lebesgue theorem. Lebesgue was aware of this result in 1898, and proved it in his 1903 dissertation. In modern terms, it is stated as: :Let \mathcal be a full cover of 'a'', ''b'' that is, a collection of closed subintervals of 'a'', ''b''wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Space
In mathematical analysis, a metric space is called complete (or a Cauchy space) if every Cauchy sequence of points in has a limit that is also in . Intuitively, a space is complete if there are no "points missing" from it (inside or at the boundary). For instance, the set of rational numbers is not complete, because e.g. \sqrt is "missing" from it, even though one can construct a Cauchy sequence of rational numbers that converges to it (see further examples below). It is always possible to "fill all the holes", leading to the ''completion'' of a given space, as explained below. Definition Cauchy sequence A sequence x_1, x_2, x_3, \ldots in a metric space (X, d) is called Cauchy if for every positive real number r > 0 there is a positive integer N such that for all positive integers m, n > N, d\left(x_m, x_n\right) < r. Complete space A metric space is complete if any of the following equivalent conditions are satisfied: :#Every |
Barrelled Space
In functional analysis and related areas of mathematics, a barrelled space (also written barreled space) is a topological vector space (TVS) for which every barrelled set in the space is a neighbourhood for the zero vector. A barrelled set or a barrel in a topological vector space is a set that is convex, balanced, absorbing, and closed. Barrelled spaces are studied because a form of the Banach–Steinhaus theorem still holds for them. Barrelled spaces were introduced by . Barrels A convex and balanced subset of a real or complex vector space is called a and it is said to be , , or . A or a in a topological vector space (TVS) is a subset that is a closed absorbing disk; that is, a barrel is a convex, balanced, closed, and absorbing subset. Every barrel must contain the origin. If \dim X \geq 2 and if S is any subset of X, then S is a convex, balanced, and absorbing set of X if and only if this is all true of S \cap Y in Y for every 2-dimensional vector subspace Y; ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexiewicz Norm
In mathematics — specifically, in integration theory — the Alexiewicz norm is an integral norm associated to the Henstock–Kurzweil integral. The Alexiewicz norm turns the space of Henstock–Kurzweil integrable functions into a topological vector space that is barrelled but not complete. The Alexiewicz norm is named after the Polish mathematician Andrzej Alexiewicz, who introduced it in 1948. Definition Let HK(R) denote the space of all functions ''f'': R → R that have finite Henstock–Kurzweil integral. Define the Alexiewicz semi-norm of ''f'' ∈ HK(R) by :\, f \, := \sup \left\. This defines a semi-norm on HK(R); if functions that are equal Lebesgue-almost everywhere are identified, then this procedure defines a ''bona fide'' norm on the quotient of HK(R) by the equivalence relation of equality almost everywhere. (Note that the only constant function ''f'': R → R that is integrable is the one with co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lebesgue Differentiation Theorem
In mathematics, the Lebesgue differentiation theorem is a theorem of real analysis, which states that for almost every point, the value of an integrable function is the limit of infinitesimal averages taken about the point. The theorem is named for Henri Lebesgue. Statement For a Lebesgue integrable real or complex-valued function ''f'' on R''n'', the indefinite integral is a set function which maps a measurable set ''A'' to the Lebesgue integral of f \cdot \mathbf_A, where \mathbf_ denotes the characteristic function of the set ''A''. It is usually written A \mapsto \int_ f\ \mathrm\lambda, with ''λ'' the ''n''–dimensional Lebesgue measure. The ''derivative'' of this integral at ''x'' is defined to be \lim_ \frac \int_f \, \mathrm\lambda, where , ''B'', denotes the volume (i.e., the Lebesgue measure) of a ball ''B'' centered at ''x'', and ''B'' → ''x'' means that the diameter of ''B'' tends to 0. The ''Lebesgue differentiation theorem'' states ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second Fundamental Theorem Of Calculus
The fundamental theorem of calculus is a theorem that links the concept of differentiating a function (calculating its slopes, or rate of change at each time) with the concept of integrating a function (calculating the area under its graph, or the cumulative effect of small contributions). The two operations are inverses of each other apart from a constant value which depends on where one starts to compute area. The first part of the theorem, the first fundamental theorem of calculus, states that for a function , an antiderivative or indefinite integral may be obtained as the integral of over an interval with a variable upper bound. This implies the existence of antiderivatives for continuous functions. Conversely, the second part of the theorem, the second fundamental theorem of calculus, states that the integral of a function over a fixed interval is equal to the change of any antiderivative between the ends of the interval. This greatly simplifies the calculation of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dominated Convergence Theorem
In measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which almost everywhere convergence of a sequence of functions implies convergence in the ''L''1 norm. Its power and utility are two of the primary theoretical advantages of Lebesgue integration over Riemann integration. In addition to its frequent appearance in mathematical analysis and partial differential equations, it is widely used in probability theory, since it gives a sufficient condition for the convergence of expected values of random variables. Statement Lebesgue's dominated convergence theorem. Let (f_n) be a sequence of complex-valued measurable functions on a measure space . Suppose that the sequence converges pointwise to a function f and is dominated by some integrable function g in the sense that : , f_n(x), \le g(x) for all numbers ''n'' in the index set of the sequence and all points x\in S. Then ''f'' is integrable (in the Lebesgue sense) and : \lim_ \int_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monotone Convergence Theorem
In the mathematical field of real analysis, the monotone convergence theorem is any of a number of related theorems proving the convergence of monotonic sequences (sequences that are non-decreasing or non-increasing) that are also bounded. Informally, the theorems state that if a sequence is increasing and bounded above by a supremum, then the sequence will converge to the supremum; in the same way, if a sequence is decreasing and is bounded below by an infimum, it will converge to the infimum. Convergence of a monotone sequence of real numbers Lemma 1 If a sequence of real numbers is increasing and bounded above, then its supremum is the limit. Proof Let (a_n)_ be such a sequence, and let \ be the set of terms of (a_n)_ . By assumption, \ is non-empty and bounded above. By the least-upper-bound property of real numbers, c = \sup_n \ exists and is finite. Now, for every \varepsilon > 0, there exists N such that a_N > c - \varepsilon , since otherwise c - \varepsilon is an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Absolute Convergence
In mathematics, an infinite series of numbers is said to converge absolutely (or to be absolutely convergent) if the sum of the absolute values of the summands is finite. More precisely, a real or complex series \textstyle\sum_^\infty a_n is said to converge absolutely if \textstyle\sum_^\infty \left, a_n\ = L for some real number \textstyle L. Similarly, an improper integral of a function, \textstyle\int_0^\infty f(x)\,dx, is said to converge absolutely if the integral of the absolute value of the integrand is finite—that is, if \textstyle\int_0^\infty , f(x), dx = L. Absolute convergence is important for the study of infinite series because its definition is strong enough to have properties of finite sums that not all convergent series possess - a convergent series that is not absolutely convergent is called conditionally convergent, while absolutely convergent series behave "nicely". For instance, rearrangements do not change the value of the sum. This is not true f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measurable Function
In mathematics and in particular measure theory, a measurable function is a function between the underlying sets of two measurable spaces that preserves the structure of the spaces: the preimage of any measurable set is measurable. This is in direct analogy to the definition that a continuous function between topological spaces preserves the topological structure: the preimage of any open set is open. In real analysis, measurable functions are used in the definition of the Lebesgue integral. In probability theory, a measurable function on a probability space is known as a random variable. Formal definition Let (X,\Sigma) and (Y,\Tau) be measurable spaces, meaning that X and Y are sets equipped with respective \sigma-algebras \Sigma and \Tau. A function f:X\to Y is said to be measurable if for every E\in \Tau the pre-image of E under f is in \Sigma; that is, for all E \in \Tau f^(E) := \ \in \Sigma. That is, \sigma (f)\subseteq\Sigma, where \sigma (f) is the σ-a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
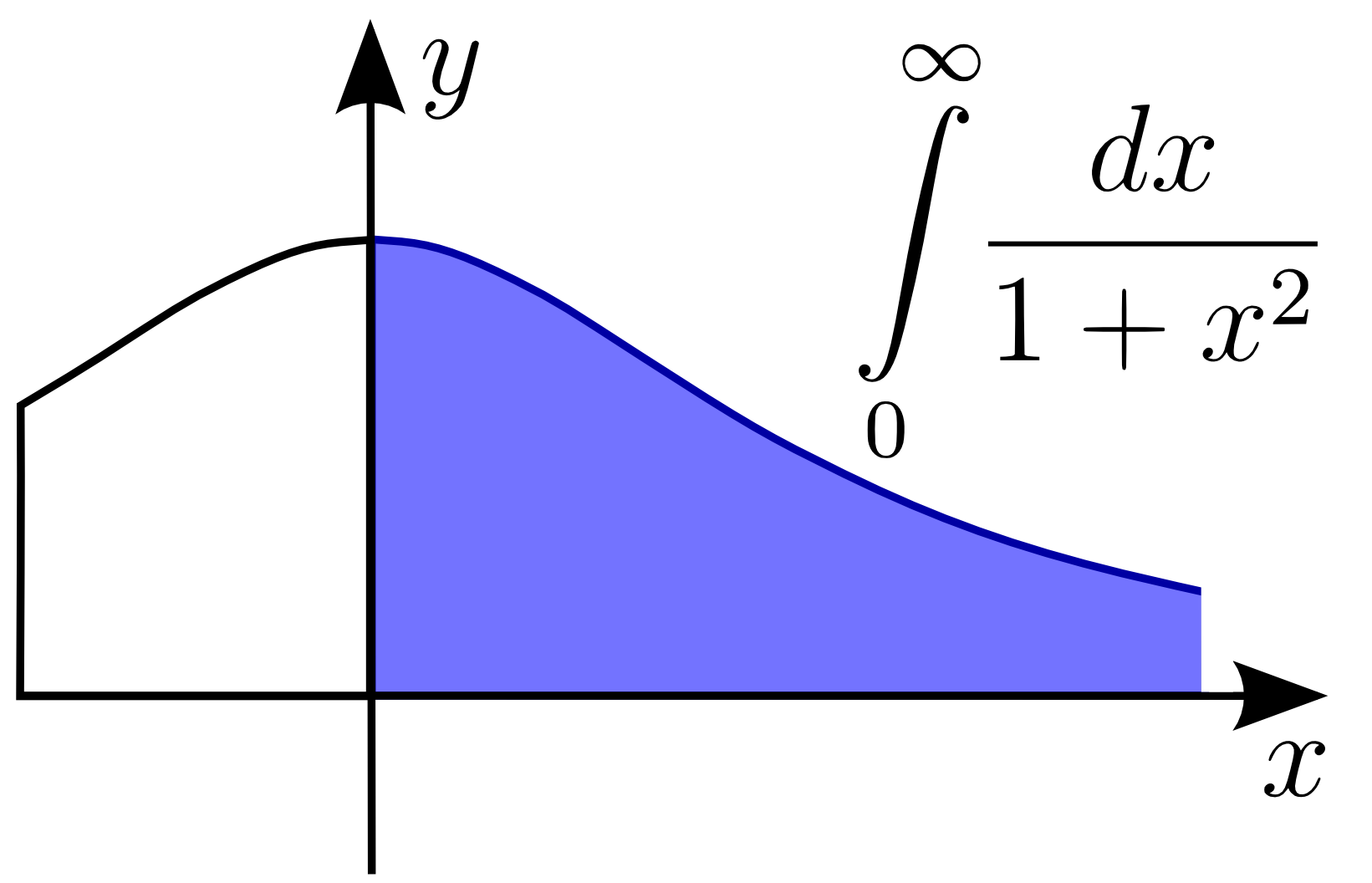
Improper Integral
In mathematical analysis, an improper integral is the limit of a definite integral as an endpoint of the interval(s) of integration approaches either a specified real number or positive or negative infinity; or in some instances as both endpoints approach limits. Such an integral is often written symbolically just like a standard definite integral, in some cases with ''infinity'' as a limit of integration. Specifically, an improper integral is a limit of the form: :\lim_ \int_a^bf(x)\, dx, \quad \lim_ \int_a^bf(x)\, dx or :\lim_ \int_a^cf(x)\ dx,\quad \lim_ \int_c^bf(x)\ dx in which one takes a limit in one or the other (or sometimes both) endpoints . By abuse of notation, improper integrals are often written symbolically just like standard definite integrals, perhaps with ''infinity'' among the limits of integration. When the definite integral exists (in the sense of either the Riemann integral or the more powerful Lebesgue integral), this ambiguity is resolved as both the pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |