|
Nonelementary Integral
In mathematics, a nonelementary antiderivative of a given elementary function is an antiderivative (or indefinite integral) that is, itself, not an elementary function.Weisstein, Eric W. "Elementary Function." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/ElementaryFunction.html From MathWorld Accessed 24 Apr 2017. A theorem by Liouville in 1835 provided the first proof that nonelementary antiderivatives exist. This theorem also provides a basis for the Risch algorithm for determining (with difficulty) which elementary functions have elementary antiderivatives. Examples Examples of functions with nonelementary antiderivatives include: *\sqrt (elliptic integral) *\frac (logarithmic integral) *e^ (error function, Gaussian integral) *\sin(x^2) and \cos(x^2) (Fresnel integral) *\frac = \operatorname(x) (sine integral, Dirichlet integral) *\frac (exponential integral) *e^ \,(in terms of the exponential integral) *\ln(\ln x) \,(in terms of the logarithmic i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Integral
In mathematics, the exponential integral Ei is a special function on the complex plane. It is defined as one particular definite integral of the ratio between an exponential function and its argument. Definitions For real non-zero values of ''x'', the exponential integral Ei(''x'') is defined as : \operatorname(x) = -\int_^\infty \fract\,dt = \int_^x \fract\,dt. The Risch algorithm shows that Ei is not an elementary function. The definition above can be used for positive values of ''x'', but the integral has to be understood in terms of the Cauchy principal value due to the singularity of the integrand at zero. For complex values of the argument, the definition becomes ambiguous due to branch points at 0 and Instead of Ei, the following notation is used, :E_1(z) = \int_z^\infty \frac\, dt,\qquad, (z), 0. Properties Several properties of the exponential integral below, in certain cases, allow one to avoid its explicit evaluation through the definition ab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Liouvillian Function
In mathematics, the Liouvillian functions comprise a set of functions including the elementary functions and their repeated integrals. Liouvillian functions can be recursively defined as integrals of other Liouvillian functions. More explicitly, a Liouvillian function is a function of one variable which is the composition of a finite number of arithmetic operations , exponentials, constants, solutions of algebraic equations (a generalization of ''n''th roots), and antiderivatives. The logarithm function does not need to be explicitly included since it is the integral of 1/x. It follows directly from the definition that the set of Liouvillian functions is closed under arithmetic operations, composition, and integration. It is also closed under differentiation. It is not closed under limits and infinite sums. Liouvillian functions were introduced by Joseph Liouville in a series of papers from 1833 to 1841. Examples All elementary functions are Liouvillian. Examples of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bounded Interval
In mathematics, a real interval is the set of all real numbers lying between two fixed endpoints with no "gaps". Each endpoint is either a real number or positive or negative infinity, indicating the interval extends without a bound. A real interval can contain neither endpoint, either endpoint, or both endpoints, excluding any endpoint which is infinite. For example, the set of real numbers consisting of , , and all numbers in between is an interval, denoted and called the unit interval; the set of all positive real numbers is an interval, denoted ; the set of all real numbers is an interval, denoted ; and any single real number is an interval, denoted . Intervals are ubiquitous in mathematical analysis. For example, they occur implicitly in the epsilon-delta definition of continuity; the intermediate value theorem asserts that the image of an interval by a continuous function is an interval; integrals of real functions are defined over an interval; etc. Interval arithmet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
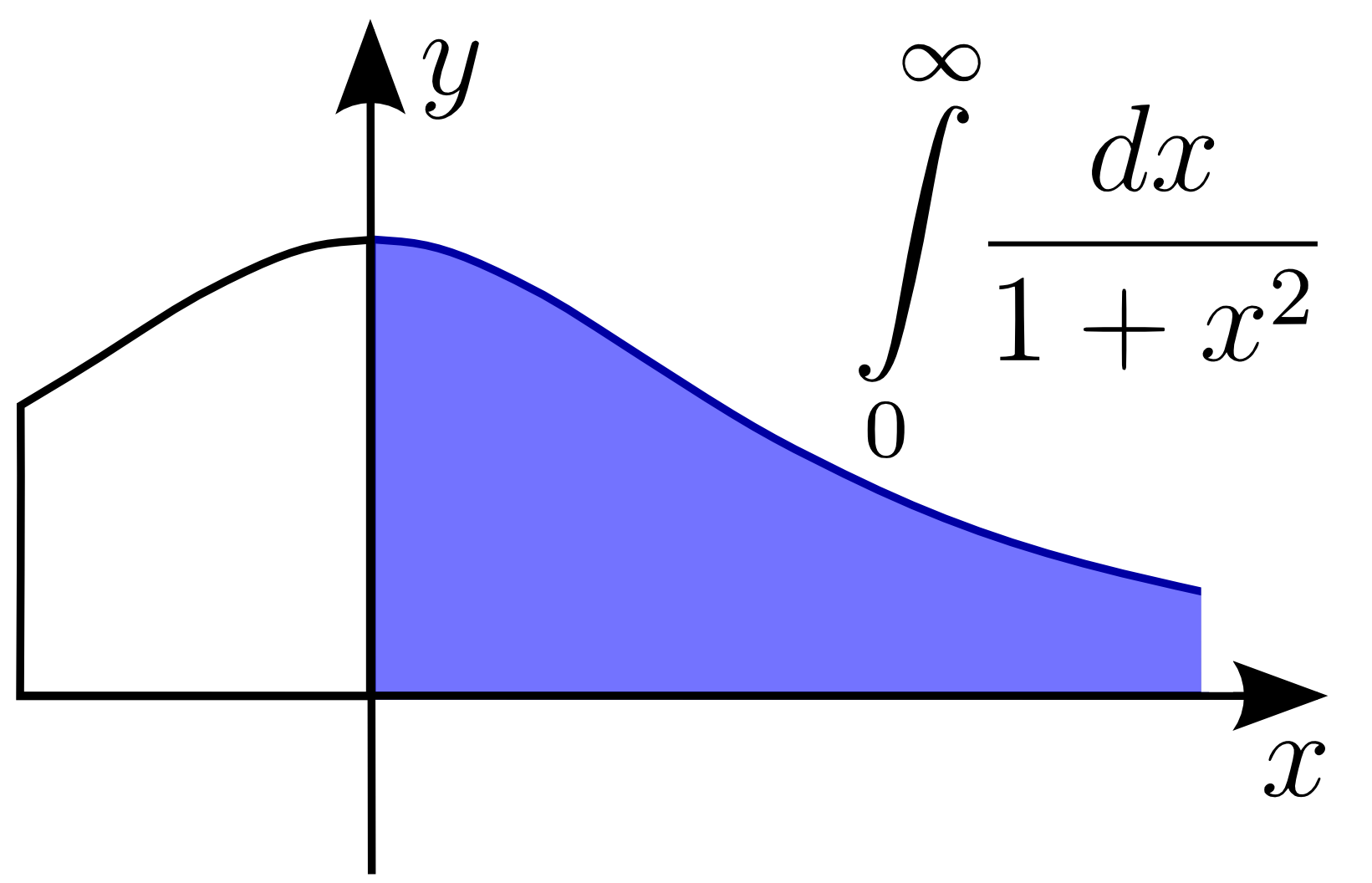
Improper Integral
In mathematical analysis, an improper integral is an extension of the notion of a definite integral to cases that violate the usual assumptions for that kind of integral. In the context of Riemann integrals (or, equivalently, Darboux integrals), this typically involves unboundedness, either of the set over which the integral is taken or of the integrand (the function being integrated), or both. It may also involve bounded but not closed sets or bounded but not continuous functions. While an improper integral is typically written symbolically just like a standard definite integral, it actually represents a limit of a definite integral or a sum of such limits; thus improper integrals are said to converge or diverge. If a regular definite integral (which may retronymically be called a proper integral) is worked out as if it is improper, the same answer will result. In the simplest case of a real-valued function of a single variable integrated in the sense of Riemann (or Darbou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Integration
In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral. The term numerical quadrature (often abbreviated to quadrature) is more or less a synonym for "numerical integration", especially as applied to one-dimensional integrals. Some authors refer to numerical integration over more than one dimension as cubature; others take "quadrature" to include higher-dimensional integration. The basic problem in numerical integration is to compute an approximate solution to a definite integral :\int_a^b f(x) \, dx to a given degree of accuracy. If is a smooth function integrated over a small number of dimensions, and the domain of integration is bounded, there are many methods for approximating the integral to the desired precision. Numerical integration has roots in the geometrical problem of finding a square with the same area as a given plane figure ('' quadrature'' or ''squaring''), as in the quadrature of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Definite Integral
In mathematics, an integral is the continuous analog of a sum, which is used to calculate areas, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. the other being differentiation. Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter. A definite integral computes the signed area of the region in the plane that is bounded by the graph of a given function between two points in the real line. Conventionally, areas above the horizontal axis of the plane are positive while areas below are negative. Integrals also refer to the concept of an ''antiderivative'', a function whose deri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radius Of Convergence
In mathematics, the radius of convergence of a power series is the radius of the largest Disk (mathematics), disk at the Power series, center of the series in which the series Convergent series, converges. It is either a non-negative real number or \infty. When it is positive, the power series absolute convergence, converges absolutely and compact convergence, uniformly on compact sets inside the open disk of radius equal to the radius of convergence, and it is the Taylor series of the analytic function to which it converges. In case of multiple singularities of a function (singularities are those values of the argument for which the function is not defined), the radius of convergence is the shortest or minimum of all the respective distances (which are all non-negative numbers) calculated from the center of the disk of convergence to the respective singularities of the function. Definition For a power series ''f'' defined as: :f(z) = \sum_^\infty c_n (z-a)^n, where *''a'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is a Expression (mathematics), mathematical expression consisting of indeterminate (variable), indeterminates (also called variable (mathematics), variables) and coefficients, that involves only the operations of addition, subtraction, multiplication and exponentiation to nonnegative integer powers, and has a finite number of terms. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problem (mathematics education), word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; and they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analytic Function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions. Functions of each type are infinitely differentiable, but complex analytic functions exhibit properties that do not generally hold for real analytic functions. A function is analytic if and only if for every x_0 in its domain, its Taylor series about x_0 converges to the function in some neighborhood of x_0 . This is stronger than merely being infinitely differentiable at x_0 , and therefore having a well-defined Taylor series; the Fabius function provides an example of a function that is infinitely differentiable but not analytic. Definitions Formally, a function f is ''real analytic'' on an open set D in the real line if for any x_0\in D one can write f(x) = \sum_^\infty a_ \left( x-x_0 \right)^ = a_0 + a_1 (x-x_0) + a_2 (x-x_0)^2 + \cdots in which the coefficients a_0, a_1, \dots a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally more accurate as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Special Functions
Special functions are particular mathematical functions that have more or less established names and notations due to their importance in mathematical analysis, functional analysis, geometry, physics, or other applications. The term is defined by consensus, and thus lacks a general formal definition, but the list of mathematical functions contains functions that are commonly accepted as special. Tables of special functions Many special functions appear as solutions of differential equations or integrals of elementary functions. Therefore, tables of integrals usually include descriptions of special functions, and tables of special functions include most important integrals; at least, the integral representation of special functions. Because symmetries of differential equations are essential to both physics and mathematics, the theory of special functions is closely related to the theory of Lie groups and Lie algebras, as well as certain topics in mathematical physics. Symbolic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
