5-cell Prism on:
[Wikipedia]
[Google]
[Amazon]
In geometry, a uniform
a,b,b,a, like ,3,3,3 doubling the symmetry order. Uniform polytopes in these group with symmetric rings contain this extended symmetry.
If all mirrors of a given color are unringed (inactive) in a given uniform polytope, it will have a lower symmetry construction by removing all of the inactive mirrors. If all the nodes of a given color are ringed (active), an alternation operation can generate a new 5-polytope with chiral symmetry, shown as "empty" circled nodes", but the geometry is not generally adjustable to create uniform solutions. ;Fundamental families
;Uniform prisms
There are 5 finite categorical uniform prismatic families of polytopes based on the nonprismatic uniform 4-polytopes. There is one infinite family of 5-polytopes based on prisms of the uniform duoprisms ××.
;Uniform duoprisms
There are 3 categorical uniform duoprismatic families of polytopes based on
;Fundamental families
;Uniform prisms
There are 5 finite categorical uniform prismatic families of polytopes based on the nonprismatic uniform 4-polytopes. There is one infinite family of 5-polytopes based on prisms of the uniform duoprisms ××.
;Uniform duoprisms
There are 3 categorical uniform duoprismatic families of polytopes based on
Coxeter diagram !colspan=5, Element counts !rowspan=2, Vertex
figure !colspan=6 , Facet counts by location: ,3,3,3, - BGCOLOR="#e0e0f0" !4, , 3, , 2, , 1, , 0 !
,3,3BR>(10) !
,3,2BR>(40) !
,2,3BR>(80) !
,3,3BR>(80) !
,3,3BR>(32) ! Alt , - BGCOLOR="#f0e0e0" !20 , , (0,0,0,0,1)√2, ,
triacontaditeron (tac)
, , 32, , 80, , 80, , 40, , 10 , ,
{3,3,4}, , - , , - , , - , , - , ,
{3,3,3}, , , - BGCOLOR="#f0e0e0" !21 , , (0,0,0,1,1)√2, , Rectified 5-orthoplex
rectified triacontaditeron (rat)
, , 42, , 240, , 400, , 240, , 40 , ,
{ }×{3,4}, ,
{3,3,4} , , - , , - , , - , ,
r{3,3,3} , , , - BGCOLOR="#f0e0e0" !22 , , (0,0,0,1,2)√2, , Truncated 5-orthoplex
truncated triacontaditeron (tot)
, , 42, , 240, , 400, , 280, , 80 , ,
(Octah.pyr), ,
{3,3,4} , , - , , - , , - , ,
t{3,3,3}, , , - BGCOLOR="#e0f0e0" !23 , , (0,0,1,1,1)√2, , Birectified 5-cube
penteractitriacontaditeron (nit)
(Birectified 5-orthoplex)
, , 42, , 280, , 640, , 480, , 80 , ,
{4}×{3}, ,
r{3,3,4} , , - , , - , , - , ,
r{3,3,3} , , , -BGCOLOR="#f0e0e0" !24 , , (0,0,1,1,2)√2, , Cantellated 5-orthoplex
small rhombated triacontaditeron (sart)
, , 82, , 640, , 1520, , 1200, , 240 , ,
Prism-wedge, ,
r{3,3,4}, ,
{ }×{3,4} , , - , , - , ,
rr{3,3,3} , , , - BGCOLOR="#f0e0e0" !25 , , (0,0,1,2,2)√2, , Bitruncated 5-orthoplex
bitruncated triacontaditeron (bittit)
, , 42, , 280, , 720, , 720, , 240 , , , ,
, , 
t{3,3,4} , , - , , - , , - , ,
2t{3,3,3} , , , - BGCOLOR="#f0e0e0" !26 , , (0,0,1,2,3)√2, ,
great rhombated triacontaditeron (gart)
, , 82, , 640, , 1520, , 1440, , 480 , , , ,
, , 
t{3,3,4}, ,
{ }×{3,4} , , -, , - , ,
t0,1,3{3,3,3} , , , - BGCOLOR="#e0e0f0" !27 , , (0,1,1,1,1)√2, ,
rectified penteract (rin)
, , 42, , 200, , 400, , 320, , 80 , ,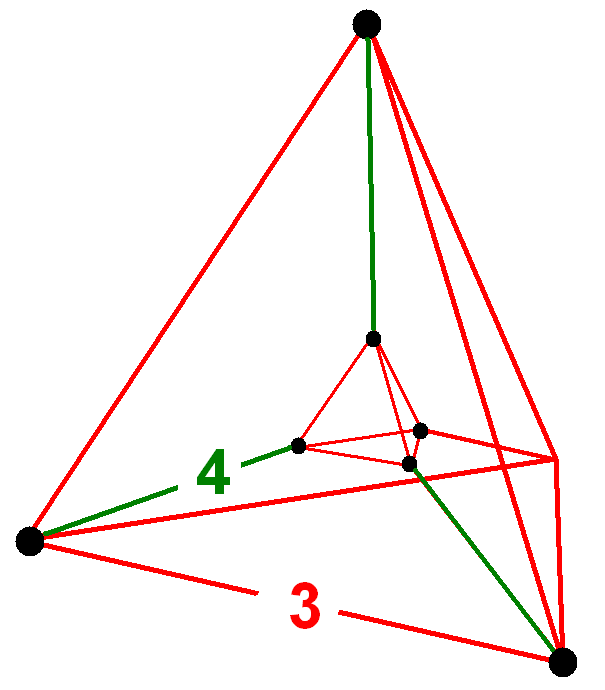
{3,3}×{ }, ,
r{4,3,3}, , - , , - , , - , ,
{3,3,3} , , , -BGCOLOR="#f0e0e0" !28 , , (0,1,1,1,2)√2, , Runcinated 5-orthoplex
small prismated triacontaditeron (spat)
, , 162, , 1200, , 2160, , 1440, , 320 , , , ,
, , 
r{4,3,3} , ,
{ }×r{3,4} , ,
{3}×{4}, , , ,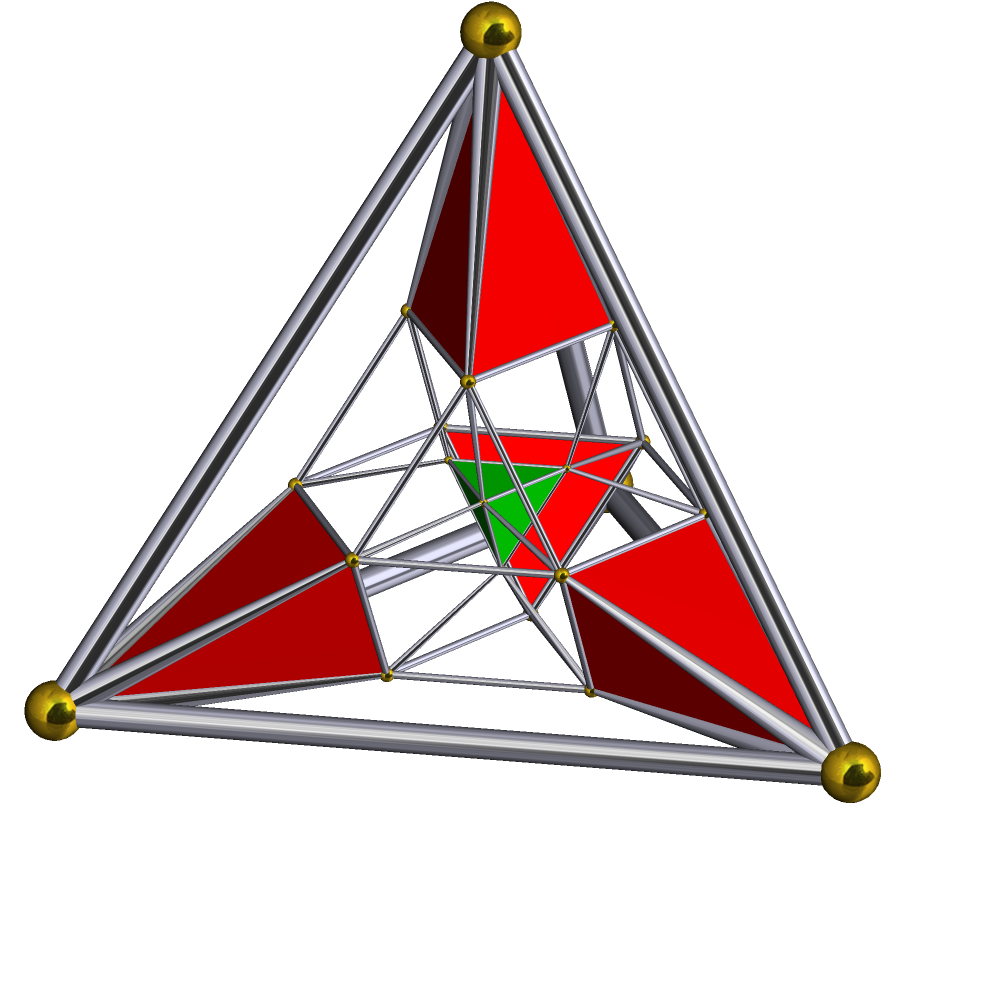
t0,3{3,3,3} , , , - BGCOLOR="#e0f0e0" !29 , , (0,1,1,2,2)√2, ,
small birhombated penteractitriacontaditeron (sibrant)
(Bicantellated 5-orthoplex)
, , 122, , 840, , 2160, , 1920, , 480 , , , ,
, , 
rr{3,3,4}, , - , ,
{4}×{3}, , - , ,
rr{3,3,3} , , , - BGCOLOR="#f0e0e0" !30 , , (0,1,1,2,3)√2, ,
prismatotruncated triacontaditeron (pattit)
, , 162, , 1440, , 3680, , 3360, , 960 , , , ,
, , 
rr{3,3,4} , ,
{ }×r{3,4} , ,
{6}×{4}, , - , ,
t0,1,3{3,3,3} , , , - BGCOLOR="#e0e0f0" !31 , , (0,1,2,2,2)√2, , Bitruncated 5-cube
bitruncated penteract (bittin)
, , 42, , 280, , 720, , 800, , 320 , ,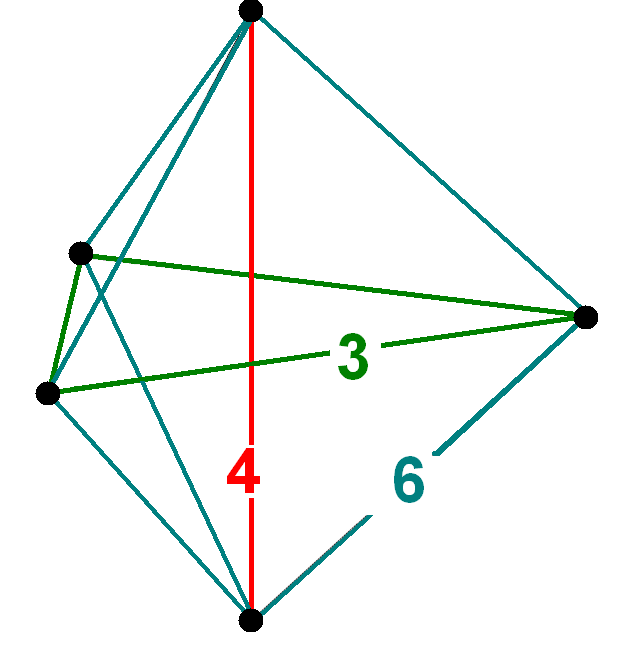 , ,
, , 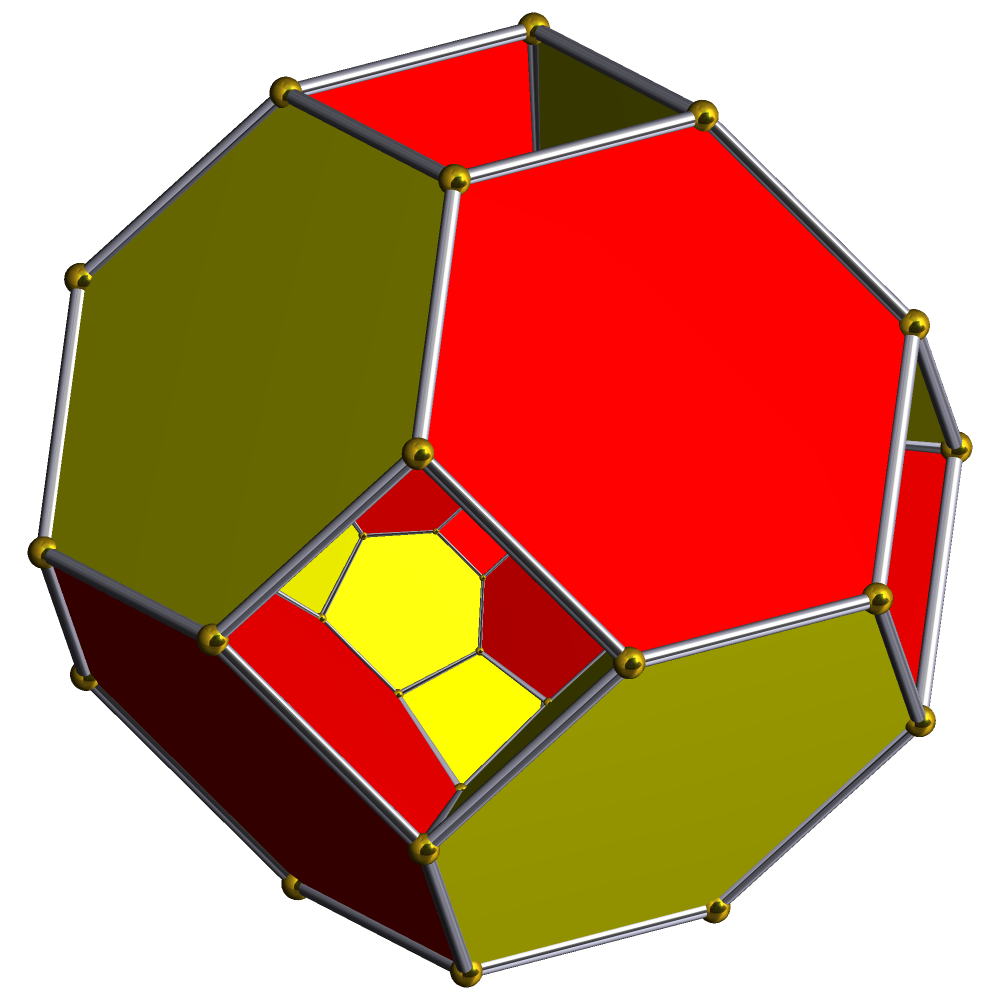
2t{4,3,3}, , - , , - , , - , ,
t{3,3,3} , , , - BGCOLOR="#f0e0e0" !32 , , (0,1,2,2,3)√2, , Runcicantellated 5-orthoplex
prismatorhombated triacontaditeron (pirt)
, , 162, , 1200, , 2960, , 2880, , 960 , ,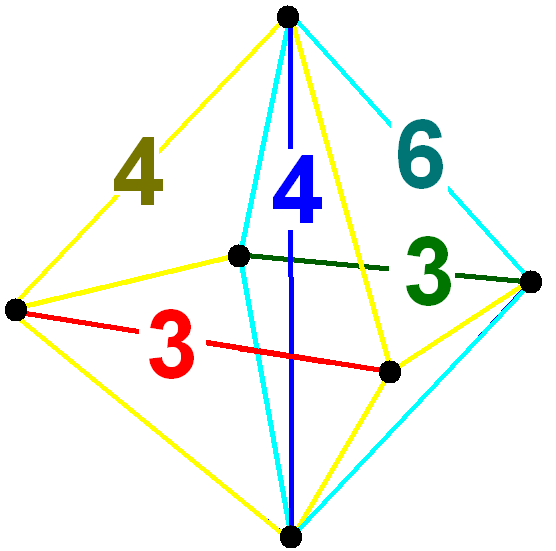 , ,
, , 
2t{4,3,3}, ,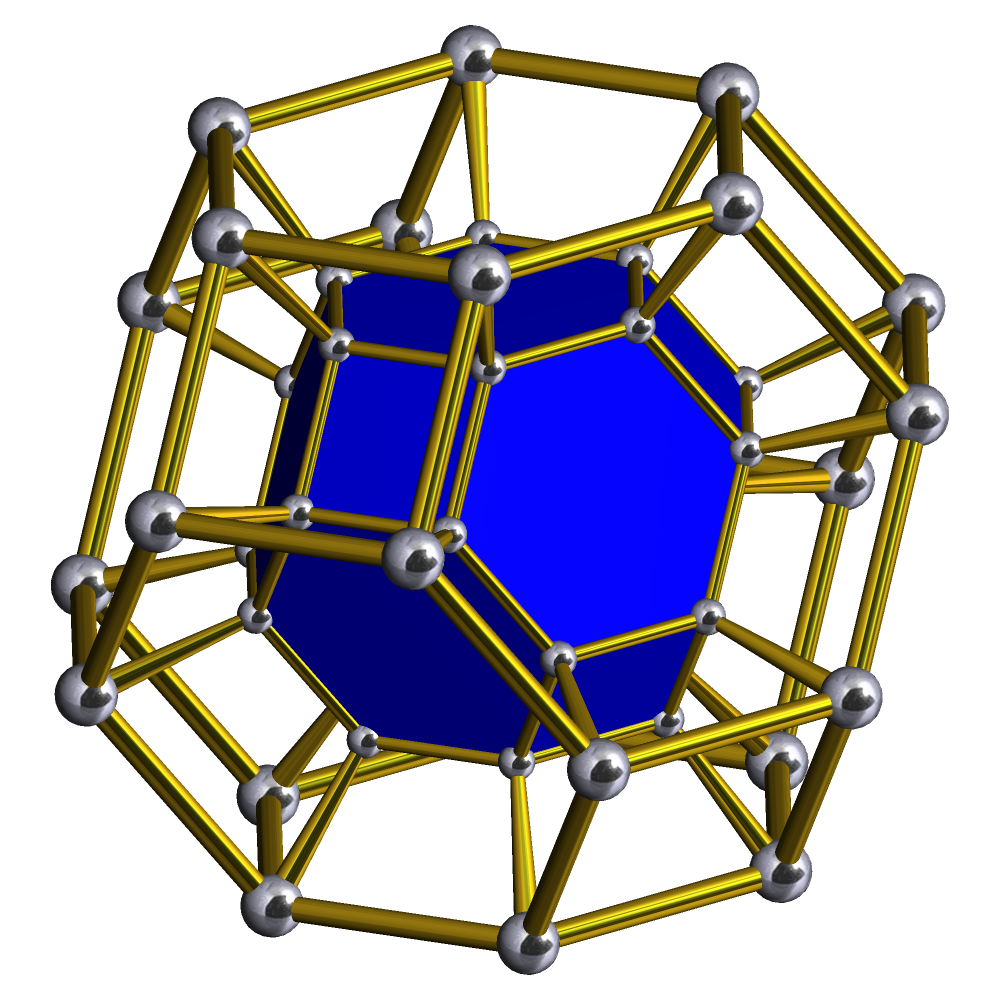
{ }×t{3,4}, ,
{3}×{4} , , - , ,
t0,1,3{3,3,3} , , , - BGCOLOR="#e0f0e0" !33 , , (0,1,2,3,3)√2, , Bicantitruncated 5-cube
great birhombated triacontaditeron (gibrant)
(Bicantitruncated 5-orthoplex)
, , 122, , 840, , 2160, , 2400, , 960 , , , ,
, , 
tr{3,3,4}, , - , ,
{4}×{3}, , - , ,
rr{3,3,3} , , , - BGCOLOR="#f0e0e0" !34 , , (0,1,2,3,4)√2, ,
great prismated triacontaditeron (gippit)
, , 162, , 1440, , 4160, , 4800, , 1920 , , , ,
, , 
tr{3,3,4} , ,
{ }×t{3,4} , ,
{6}×{4}, , - , ,
t0,1,2,3{3,3,3} , , , - BGCOLOR="#e0e0f0" !35 , , (1,1,1,1,1), ,
penteract (pent)
, , 10, , 40, , 80, , 80, , 32 , ,
{3,3,3}, ,
{4,3,3}, , - , , - , , - , , - , , , - BGCOLOR="#e0f0e0" !36 , , (1,1,1,1,1)
+ (0,0,0,0,1)√2, , Stericated 5-cube
small cellated penteractitriacontaditeron (scant)
(Stericated 5-orthoplex)
, , 242, , 800, , 1040, , 640, , 160 , ,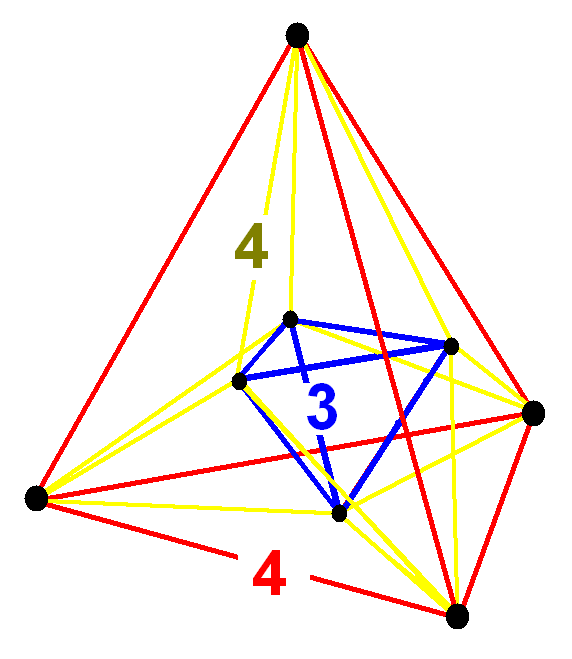
Tetr.antiprm, ,
{4,3,3}, ,
{4,3}×{ }, ,
{4}×{3}, ,
{ }×{3,3}, ,
{3,3,3} , , , - BGCOLOR="#e0e0f0" !37 , , (1,1,1,1,1)
+ (0,0,0,1,1)√2, , Runcinated 5-cube
small prismated penteract (span)
, , 202, , 1240, , 2160, , 1440, , 320 , , , ,
, , 
t0,3{4,3,3}, , - , ,
{4}×{3}, ,
{ }×r{3,3}, ,
r{3,3,3} , , , - BGCOLOR="#f0e0e0" !38 , , (1,1,1,1,1)
+ (0,0,0,1,2)√2, , Steritruncated 5-orthoplex
celliprismated triacontaditeron (cappin)
, , 242, , 1520, , 2880, , 2240, , 640 , , , ,
, , 
t0,3{4,3,3} , ,
{4,3}×{ } , ,
{6}×{4} , ,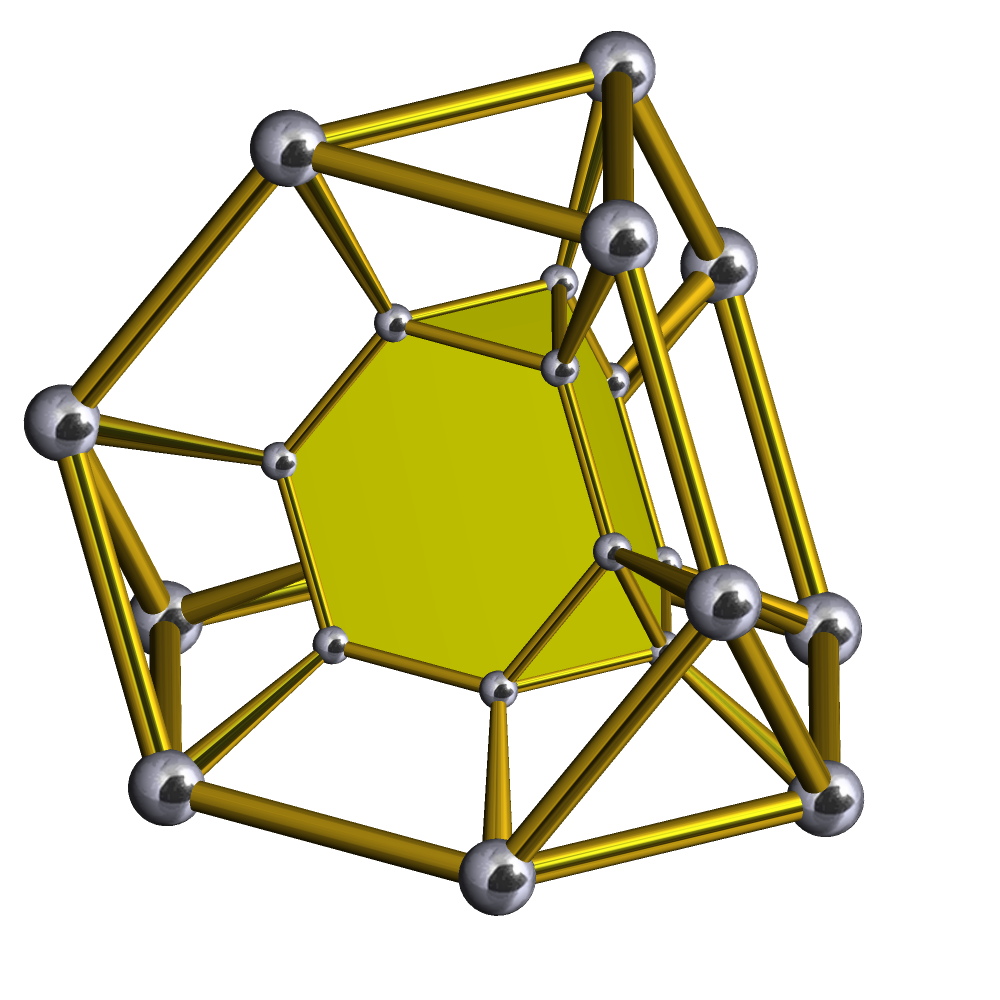
{ }×t{3,3} , ,
t{3,3,3} , , , - BGCOLOR="#e0e0f0" !39 , , (1,1,1,1,1)
+ (0,0,1,1,1)√2, , Cantellated 5-cube
small rhombated penteract (sirn)
, , 122, , 680, , 1520, , 1280, , 320 , ,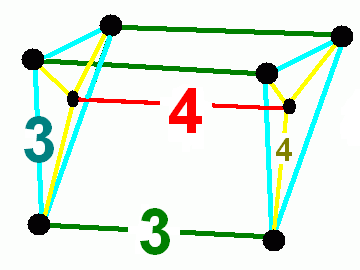
Prism-wedge, ,
rr{4,3,3}, , - , , - , ,
{ }×{3,3}, ,
r{3,3,3} , , , - BGCOLOR="#e0f0e0" !40 , , (1,1,1,1,1)
+ (0,0,1,1,2)√2, ,
cellirhombated penteractitriacontaditeron (carnit)
(Stericantellated 5-orthoplex)
, , 242, , 2080, , 4720, , 3840, , 960 , , , ,
, , 
rr{4,3,3}, ,
rr{4,3}×{ }, ,
{4}×{3}, ,
{ }×rr{3,3}, ,
rr{3,3,3} , , , - BGCOLOR="#e0e0f0" !41 , , (1,1,1,1,1)
+ (0,0,1,2,2)√2, ,
prismatorhombated penteract (prin)
, , 202, , 1240, , 2960, , 2880, , 960 , ,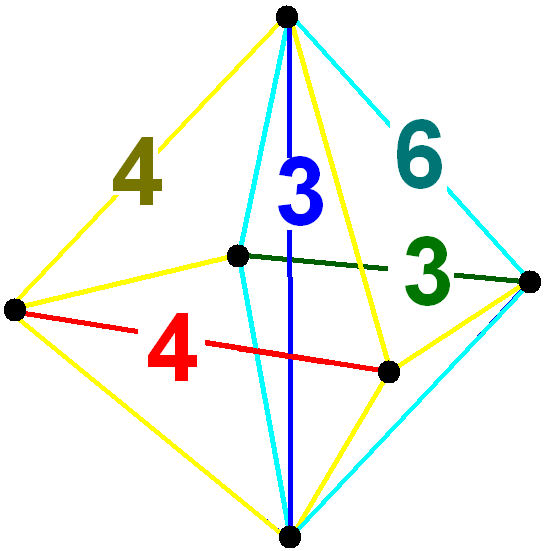 , ,
, , 
t0,2,3{4,3,3}, , - , ,
{4}×{3}, ,
{ }×t{3,3}, ,
2t{3,3,3} , , , - BGCOLOR="#f0e0e0" !42 , , (1,1,1,1,1)
+ (0,0,1,2,3)√2, , Stericantitruncated 5-orthoplex
celligreatorhombated triacontaditeron (cogart)
, , 242, , 2320, , 5920, , 5760, , 1920 , ,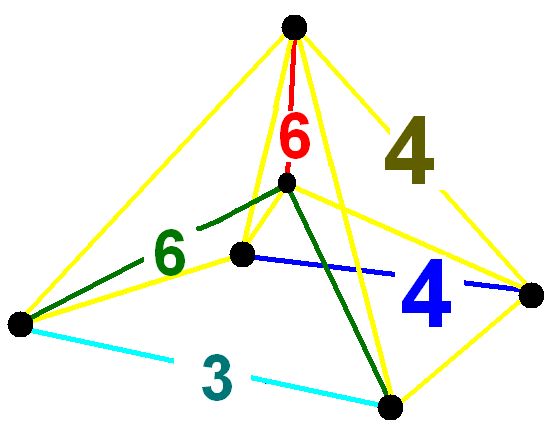 , ,
, , 
t0,2,3{4,3,3}, ,
rr{4,3}×{ }, ,
{6}×{4}, ,
{ }×tr{3,3}, ,
tr{3,3,3} , , , - BGCOLOR="#e0e0f0" !43 , , (1,1,1,1,1)
+ (0,1,1,1,1)√2, ,
truncated penteract (tan)
, , 42, , 200, , 400, , 400, , 160 , ,
Tetrah.pyr, ,
t{4,3,3}, , - , , - , , - , ,
{3,3,3} , , , - BGCOLOR="#e0e0f0" !44 , , (1,1,1,1,1)
+ (0,1,1,1,2)√2, , Steritruncated 5-cube
celliprismated triacontaditeron (capt)
, , 242, , 1600, , 2960, , 2240, , 640 , , , ,
, , 
t{4,3,3}, ,
t{4,3}×{ }, ,
{8}×{3}, ,
{ }×{3,3}, ,
t0,3{3,3,3} , , , - BGCOLOR="#e0e0f0" !45 , , (1,1,1,1,1)
+ (0,1,1,2,2)√2, ,
prismatotruncated penteract (pattin)
, , 202, , 1560, , 3760, , 3360, , 960 , ,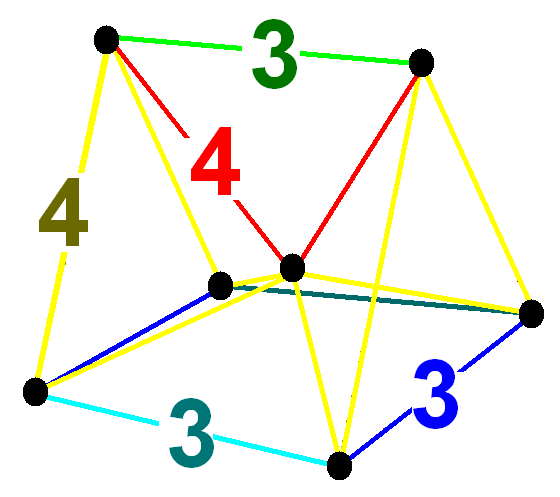 , ,
, , 
t0,1,3{4,3,3} , , - , ,
{8}×{3}, ,
{ }×r{3,3} , ,
rr{3,3,3} , , , - BGCOLOR="#e0f0e0" !46 , , (1,1,1,1,1)
+ (0,1,1,2,3)√2, , Steriruncitruncated 5-cube
celliprismatotruncated penteractitriacontaditeron (captint)
(Steriruncitruncated 5-orthoplex)
, , 242, , 2160, , 5760, , 5760, , 1920 , , , ,
, , 
t0,1,3{4,3,3}, ,
t{4,3}×{ }, ,
{8}×{6}, ,
{ }×t{3,3}, ,
t0,1,3{3,3,3} , , , - BGCOLOR="#e0e0f0" !47 , , (1,1,1,1,1)
+ (0,1,2,2,2)√2, , Cantitruncated 5-cube
great rhombated penteract (girn)
, , 122, , 680, , 1520, , 1600, , 640 , , , ,
, , 
tr{4,3,3}, , - , , - , ,
{ }×{3,3}, ,
t{3,3,3} , , , - BGCOLOR="#e0e0f0" !48 , , (1,1,1,1,1)
+ (0,1,2,2,3)√2, ,
celligreatorhombated penteract (cogrin)
, , 242, , 2400, , 6000, , 5760, , 1920 , , , ,
, , 
tr{4,3,3}, ,
tr{4,3}×{ }, ,
{8}×{3}, ,
{ }×rr{3,3}, ,
t0,1,3{3,3,3} , , , - BGCOLOR="#e0e0f0" !49 , , (1,1,1,1,1)
+ (0,1,2,3,3)√2, ,
great prismated penteract (gippin)
, , 202, , 1560, , 4240, , 4800, , 1920 , , , ,
, , 
t0,1,2,3{4,3,3}, , - , ,
{8}×{3}, ,
{ }×t{3,3}, ,
tr{3,3,3} , , , - BGCOLOR="#e0f0e0" !50 , , (1,1,1,1,1)
+ (0,1,2,3,4)√2, ,
great cellated penteractitriacontaditeron (gacnet)
(omnitruncated 5-orthoplex)
, , 242, , 2640, , 8160, , 9600, , 3840 , ,
Irr. {3,3,3}, ,
tr{4,3}×{ }, ,
tr{4,3}×{ }, ,
{8}×{6}, ,
{ }×tr{3,3}, ,
t0,1,2,3{3,3,3} , , , - BGCOLOR="#d0f0f0" !51 , ,
hemipenteract (hin)
= , 26 , 120 , 160 , 80 , 16 ,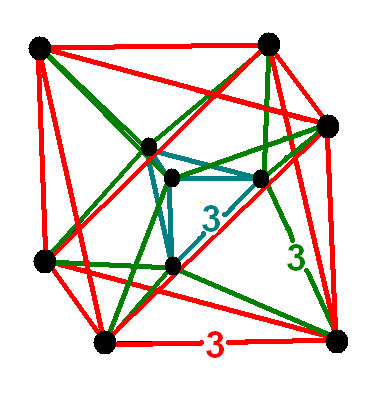
r{3,3,3} ,
h{4,3,3} , - , - , - , - , (16)

{3,3,3} , - BGCOLOR="#d0f0f0" !52 , , Cantic 5-cube
Truncated hemipenteract (thin)
= , 42 , 280 , 640 , 560 , 160 ,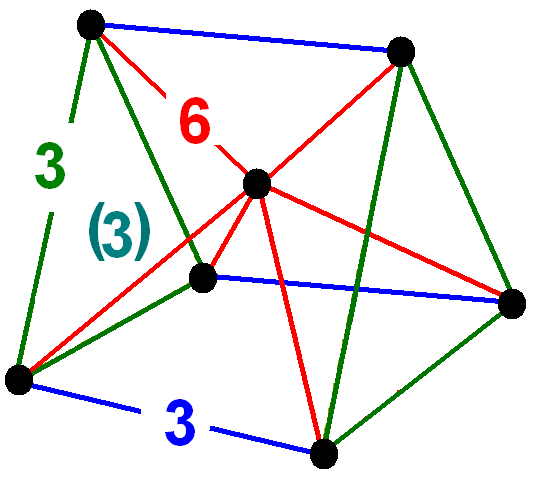 ,
, 
h2{4,3,3} , - , - , - , (16)

r{3,3,3} , (16)

t{3,3,3} , - BGCOLOR="#d0f0f0" !53 , ,
Small rhombated hemipenteract (sirhin)
= , 42 , 360 , 880 , 720 , 160 , ,
h3{4,3,3} , - , - , - , (16)

r{3,3,3} , (16)

rr{3,3,3} , - BGCOLOR="#d0f0f0" !54 , , Steric 5-cube
Small prismated hemipenteract (siphin)
= , 82 , 480 , 720 , 400 , 80 , ,
h{4,3,3} ,
h{4,3}×{} , - , - , (16)

{3,3,3} , (16)

t0,3{3,3,3} , - BGCOLOR="#d0f0f0" !55 , ,
Great rhombated hemipenteract (girhin)
= , 42 , 360 , 1040 , 1200 , 480 , ,
h2,3{4,3,3} , - , - , - , (16)

2t{3,3,3} , (16)

tr{3,3,3} , - BGCOLOR="#d0f0f0" !56 , ,
Prismatotruncated hemipenteract (pithin)
= , 82 , 720 , 1840 , 1680 , 480 , ,
h2{4,3,3} ,
h2{4,3}×{} , - , - , (16)

rr{3,3,3} , (16)

t0,1,3{3,3,3} , - BGCOLOR="#d0f0f0" !57 , ,
Prismatorhombated hemipenteract (pirhin)
= , 82 , 560 , 1280 , 1120 , 320 , ,
h3{4,3,3} ,
h{4,3}×{} , - , - , (16)

t{3,3,3} , (16)

t0,1,3{3,3,3} , - BGCOLOR="#d0f0f0" !58 , ,
Great prismated hemipenteract (giphin)
= , 82 , 720 , 2080 , 2400 , 960 , ,
h2,3{4,3,3} ,
h2{4,3}×{} , - , - , (16)

tr{3,3,3} , (16)

t0,1,2,3{3,3,3} , - BGCOLOR="#d0f0f0" !Nonuniform , , Alternated runcicantitruncated 5-orthoplex
Snub prismatotriacontaditeron (snippit)
Snub hemipenteract (snahin)
= , 1122 , 6240 , 10880 , 6720 , 960 , ,
sr{3,3,4} , sr{2,3,4} , sr{3,2,4} , - , ht0,1,2,3{3,3,3} , (960)

Irr. {3,3,3} , - BGCOLOR="#d0f0f0" !Nonuniform , , Edge-snub 5-orthoplex
Pyritosnub penteract (pysnan)
, 1202 , 7920 , 15360 , 10560 , 1920 , , sr3{3,3,4} , sr3{2,3,4} , sr3{3,2,4} ,
s{3,3}×{ } , ht0,1,2,3{3,3,3} , (960)

Irr. {3,3}×{ } , - BGCOLOR="#d0f0f0" !Nonuniform , , Snub 5-cube
Snub penteract (snan)
, 2162 , 12240 , 21600 , 13440 , 960 , , ht0,1,2,3{3,3,4} , ht0,1,2,3{2,3,4} , ht0,1,2,3{3,2,4} , ht0,1,2,3{3,3,2} , ht0,1,2,3{3,3,3} , (1920)

Irr. {3,3,3}
Johnson and Bowers names !colspan=5, Element counts !rowspan=2, Vertex
figure !colspan=6 , Facets by location: 1,2,1 , - !4 !3 !2 !1 !0 !
,3,3BR>(16) !
1,1,1BR>(10) !
,3� nbsp;BR>(40) !
nbsp;� � nbsp;BR>(80) !
,3,3BR>(16) ! Alt , - ! 1, =
h{4,3,3,3},
Hemipenteract (hin) , 26 , 120 , 160 , 80 , 16 ,
r{3,3,3} ,
{3,3,3} ,
h{4,3,3} , - , - , - , , - ! 2, =
h2{4,3,3,3}, cantic 5-cube
Truncated hemipenteract (thin) , 42 , 280 , 640 , 560 , 160 , ,
t{3,3,3} ,
h2{4,3,3} , - , - ,
r{3,3,3} , , - ! 3, =
h3{4,3,3,3},
Small rhombated hemipenteract (sirhin) , 42 , 360 , 880 , 720 , 160 , ,
rr{3,3,3} ,
h3{4,3,3} , - , - ,
r{3,3,3} , , - ! 4, =
h4{4,3,3,3}, steric 5-cube
Small prismated hemipenteract (siphin) , 82 , 480 , 720 , 400 , 80 , ,
t0,3{3,3,3} ,
h{4,3,3} ,
h{4,3}×{} , - ,
{3,3,3} , , - ! 5, =
h2,3{4,3,3,3},
Great rhombated hemipenteract (girhin) , 42 , 360 , 1040 , 1200 , 480 , ,
2t{3,3,3} ,
h2,3{4,3,3} , - , - ,
tr{3,3,3} , , - ! 6, =
h2,4{4,3,3,3},
Prismatotruncated hemipenteract (pithin) , 82 , 720 , 1840 , 1680 , 480 , ,
t0,1,3{3,3,3} ,
h2{4,3,3} ,
h2{4,3}×{} , - ,
rr{3,3,3} , , - ! 7, =
h3,4{4,3,3,3},
Prismatorhombated hemipenteract (pirhin) , 82 , 560 , 1280 , 1120 , 320 , ,
t0,1,3{3,3,3} ,
h3{4,3,3} ,
h{4,3}×{} , - ,
t{3,3,3} , , - ! 8, =
h2,3,4{4,3,3,3},
Great prismated hemipenteract (giphin) , 82 , 720 , 2080 , 2400 , 960 , ,
t0,1,2,3{3,3,3} ,
h2,3{4,3,3} ,
h2{4,3}×{} , - ,
tr{3,3,3} , , - bgcolor="#D0F0F0" ! Nonuniform , =
ht0,1,2,3{3,3,3,4}, alternated runcicantitruncated 5-orthoplex
Snub hemipenteract (snahin) , 1122 , 6240 , 10880 , 6720 , 960 , , ht0,1,2,3{3,3,3} ,
sr{3,3,4} , sr{2,3,4} , sr{3,2,4} , ht0,1,2,3{3,3,3} , (960)
Irr. {3,3,3}
and Schläfli
symbols
Name !colspan=5 rowspan=1, Element counts , - ! Facets, , Cells, , Faces, , Edges, , Vertices , - , 59 , = {3,3,3}×{ }
Cantellated 5-cell prism (srippip) , 22, , 120, , 250, , 210, , 60 , - BGCOLOR="#e0f0e0" , 63 , = t0,3{3,3,3}×{ }
Cantitruncated 5-cell prism (grippip) , 22, , 120, , 280, , 300, , 120 , - , 66 , = t0,1,3{3,3,3}×{ }
Runcitruncated 5-cell prism (prippip) , 32, , 180, , 390, , 360, , 120 , - BGCOLOR="#e0f0e0" , 67 , = t0,1,2,3{3,3,3}×{ }
Omnitruncated 5-cell prism (gippiddip) , 32, , 210, , 540, , 600, , 240
and Schläfli
symbols
Name !colspan=5 rowspan=1, Element counts , - ! Facets, , Cells, , Faces, , Edges, , Vertices , - BGCOLOR="#f0e0e0" , 6'', , = {4,3,3}×{ }
Tesseractic prism (pent)
(Same as
Cantellated tesseractic prism (srittip) , 58, , 360, , 784, , 672, , 192 , - BGCOLOR="#e0f0e0" , 71, , = t0,3{4,3,3}×{ }
Runcinated tesseractic prism (sidpithip) , 82, , 368, , 608, , 448, , 128 , - BGCOLOR="#e0f0e0" , 72, , = 2t{4,3,3}×{ }
Bitruncated tesseractic prism (tahp) , 26, , 168, , 432, , 480, , 192 , - BGCOLOR="#f0e0e0" , 73, , = tr{4,3,3}×{ }
Cantitruncated tesseractic prism (grittip) , 58, , 360, , 880, , 960, , 384 , - BGCOLOR="#f0e0e0" , 74, , = t0,1,3{4,3,3}×{ }
Runcitruncated tesseractic prism (prohp) , 82, , 528, , 1216, , 1152, , 384 , - BGCOLOR="#e0f0e0" , 75, , = t0,1,2,3{4,3,3}×{ }
Rectified 16-cell prism (icope)
(Same as 24-cell prism) , 26, , 144, , 288, , 216, , 48 , - BGCOLOR="#e0e0f0" , 78, , = t{3,3,4}×{ }
Cantellated 16-cell prism (ricope)
(Same as rectified 24-cell prism) , 50, , 336, , 768, , 672, , 192 , - BGCOLOR="#e0e0f0" , 80, , = tr{3,3,4}×{ }
Cantitruncated 16-cell prism (ticope)
(Same as truncated 24-cell prism) , 50, , 336, , 864, , 960, , 384 , - BGCOLOR="#e0e0f0" , 81, , = t0,1,3{3,3,4}×{ }
Runcitruncated 16-cell prism (prittip) , 82, , 528, , 1216, , 1152, , 384 , - BGCOLOR="#a0e0f0" , 82, , = sr{3,3,4}×{ }
rectified tesseractic alterprism (rita) , 50, , 288, , 464, , 288, , 64 , - BGCOLOR="#a0e0f0" , Nonuniform, ,
truncated 16-cell alterprism (thexa) , 26, , 168, , 384, , 336, , 96 , - BGCOLOR="#a0e0f0" , Nonuniform, ,
bitruncated tesseractic alterprism (taha) , 50, , 288, , 624, , 576, , 192
and Schläfli
symbols
Name !colspan=5 rowspan=1, Element counts , - ! Facets, , Cells, , Faces, , Edges, , Vertices , - , 7, = {3,4,3}×{ }
24-cell prism (icope) , 26, , 144, , 288, , 216, , 48 , - , 9, = r{3,4,3}×{ }
rectified 24-cell prism (ricope) , 50, , 336, , 768, , 672, , 192 , - , 0, = t{3,4,3}×{ }
cantellated 24-cell prism (sricope) , 146, , 1008, , 2304, , 2016, , 576 , - BGCOLOR="#b0f0b0" , 84, , = t0,3{3,4,3}×{ }
runcinated 24-cell prism (spiccup) , 242, , 1152, , 1920, , 1296, , 288 , - BGCOLOR="#b0f0b0" , 85, , = 2t{3,4,3}×{ }
bitruncated 24-cell prism (contip) , 50, , 432, , 1248, , 1440, , 576 , - , 86, , = tr{3,4,3}×{ }
cantitruncated 24-cell prism (gricope) , 146, , 1008, , 2592, , 2880, , 1152 , - , 87, , = t0,1,3{3,4,3}×{ }
runcitruncated 24-cell prism (pricope) , 242, , 1584, , 3648, , 3456, , 1152 , - BGCOLOR="#b0f0b0" , 88, , = t0,1,2,3{3,4,3}×{ }
omnitruncated 24-cell prism (gippiccup) , 242, , 1872, , 5088, , 5760, , 2304 , - BGCOLOR="#b0e0f0" , 2, = s{3,4,3}×{ }
and Schläfli
symbols
Name !colspan=5 rowspan=1, Element counts , - ! Facets, , Cells, , Faces, , Edges, , Vertices , - BGCOLOR="#f0e0e0" , 89, , = {5,3,3}×{ }
120-cell prism (hipe) , 122, , 960, , 2640, , 3000, , 1200 , - BGCOLOR="#f0e0e0" , 90, , = r{5,3,3}×{ }
Rectified 120-cell prism (rahipe) , 722, , 4560, , 9840, , 8400, , 2400 , - BGCOLOR="#f0e0e0" , 91, , = t{5,3,3}×{ }
Truncated 120-cell prism (thipe) , 722, , 4560, , 11040, , 12000, , 4800 , - BGCOLOR="#f0e0e0" , 92, , = rr{5,3,3}×{ }
Cantellated 120-cell prism (srahip) , 1922, , 12960, , 29040, , 25200, , 7200 , - BGCOLOR="#e0f0e0" , 93, , = t0,3{5,3,3}×{ }
Bitruncated 120-cell prism (xhip) , 722, , 5760, , 15840, , 18000, , 7200 , - BGCOLOR="#f0e0e0" , 95, , = tr{5,3,3}×{ }
Cantitruncated 120-cell prism (grahip) , 1922, , 12960, , 32640, , 36000, , 14400 , - BGCOLOR="#f0e0e0" , 96, , = t0,1,3{5,3,3}×{ }
Runcitruncated 120-cell prism (prixip) , 2642, , 18720, , 44880, , 43200, , 14400 , - BGCOLOR="#e0f0e0" , 97, , = t0,1,2,3{5,3,3}×{ }
Truncated 600-cell prism (texip) , 722, , 5040, , 11520, , 10080, , 2880 , - BGCOLOR="#e0e0f0" , 101, , = rr{3,3,5}×{ }
Cantellated 600-cell prism (srixip) , 1442, , 11520, , 28080, , 25200, , 7200 , - BGCOLOR="#e0e0f0" , 102, , = tr{3,3,5}×{ }
Cantitruncated 600-cell prism (grixip) , 1442, , 11520, , 31680, , 36000, , 14400 , - BGCOLOR="#e0e0f0" , 103, , = t0,1,3{3,3,5}×{ }
Runcitruncated 600-cell prism (prahip) , 2642, , 18720, , 44880, , 43200, , 14400
, - align=center ! Cantellated , t0,2{p,q,r,s}, , rr{p,q,r,s} , , align=left, In addition to vertex truncation, each original edge is ''beveled'' with new rectangular faces appearing in their place.
, - align=center ! Runcinated , colspan=2, t0,3{p,q,r,s} , , align=left, Runcination reduces cells and creates new cells at the vertices and edges. , - align=center ! Stericated , t0,4{p,q,r,s}, , 2r2r{p,q,r,s} , , align=left, Sterication reduces facets and creates new facets (hypercells) at the vertices and edges in the gaps. (Same as expansion operation for 5-polytopes.) , - align=center !
= [4,3,3,5]:
= ,3,3,5 There are 5 regular compact convex hyperbolic honeycombs in H4 space:Coxeter, The Beauty of Geometry: Twelve Essays, Chapter 10: Regular honeycombs in hyperbolic space, Summary tables IV p213 {, class="wikitable" , + Compact regular convex hyperbolic honeycombs , - !Honeycomb name ! Schläfli
Symbol
{p,q,r,s} ! Coxeter diagram !Facet
type
{p,q,r} !Cell
type
{p,q} !Face
type
{p} !Face
figure
{s} !Edge
figure
{r,s} ! Vertex
figure
{q,r,s} !
Symbol
{p,q,r,s} ! Coxeter diagram !Facet
type
{p,q,r} !Cell
type
{p,q} !Face
type
{p} !Face
figure
{s} !Edge
figure
{r,s} ! Vertex
figure
{q,r,s} !
= [(3,3,4,3,4)]:
= [3 �[]]: , align= = ,/3\,3,4
= ,4,31,1
= ,32,1
= ,31,1,1 , align= = ,4,3,4
** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', ath. Zeit. 46 (1940) 380-407, MR 2,10** (Paper 23) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes II'', ath. Zeit. 188 (1985) 559-591(p. 287 5D Euclidean groups, p. 298 Four-dimensionsal honeycombs) ** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', ath. Zeit. 200 (1988) 3-45* N.W. Johnson: ''The Theory of Uniform Polytopes and Honeycombs'', Ph.D. Dissertation, University of Toronto, 1966 * James E. Humphreys, ''Reflection Groups and Coxeter Groups'', Cambridge studies in advanced mathematics, 29 (1990) (Page 141, 6.9 List of hyperbolic Coxeter groups, figure 2
5-polytope
In geometry, a five-dimensional polytope (or 5-polytope) is a polytope in five-dimensional space, bounded by (4-polytope) facets, pairs of which share a polyhedral cell.
Definition
A 5-polytope is a closed five-dimensional figure with vertices ...
is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope facets.
The complete set of convex uniform 5-polytopes has not been determined, but many can be made as Wythoff constructions from a small set of symmetry groups
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient ...
. These construction operations are represented by the permutations of rings of the Coxeter diagrams.
History of discovery
* Regular polytopes: (convex faces) **1852: Ludwig Schläfli proved in his manuscript ''Theorie der vielfachen Kontinuität'' that there are exactly 3 regular polytopes in 5 or more dimensions. *Convex semiregular polytopes: (Various definitions before Coxeter's uniform category) **1900: Thorold Gosset enumerated the list of nonprismatic semiregular convex polytopes with regular facets ( convex regular 4-polytopes) in his publication ''On the Regular and Semi-Regular Figures in Space of n Dimensions''. *Convex uniform polytopes: **1940-1988: The search was expanded systematically byH.S.M. Coxeter
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century.
Biography
Coxeter was born in Kensington t ...
in his publication ''Regular and Semi-Regular Polytopes I, II, and III''.
**1966: Norman W. Johnson
Norman Woodason Johnson () was a mathematician at Wheaton College, Norton, Massachusetts.
Early life and education
Norman Johnson was born on in Chicago. His father had a bookstore and published a local newspaper.
Johnson earned his unde ...
completed his Ph.D. Dissertation under Coxeter, ''The Theory of Uniform Polytopes and Honeycombs'', University of Toronto
* Non-convex uniform polytopes:
**1966: Johnson describes two non-convex uniform antiprisms in 5-space in his dissertation.
**2000-2022: Jonathan Bowers and other researchers search for other non-convex uniform 5-polytopes, with a current count of 1294 known uniform 5-polytopes outside infinite families (convex and non-convex), excluding the prisms of the uniform 4-polytopes. The list is not proven complete.
Regular 5-polytopes
Regular 5-polytopes can be represented by theSchläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
, with s 4-polytope facets around each face. There are exactly three such regular polytopes, all convex:
* - 5-simplex
In five-dimensional geometry, a 5-simplex is a self-dual regular 5-polytope. It has six vertices, 15 edges, 20 triangle faces, 15 tetrahedral cells, and 6 5-cell facets. It has a dihedral angle of cos−1(), or approximately 78.46°.
The 5-s ...
* - 5-cube
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.
It is represented by Schläfli symbol or , constructed as 3 tesseracts, ...
* - 5-orthoplex
In five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell 4-faces.
It has two constructed forms, the first being regular with ...
There are no nonconvex regular polytopes in 5 dimensions or above.
Convex uniform 5-polytopes
There are 104 known convex uniform 5-polytopes, plus a number of infinite families of duoprism prisms, and polygon-polyhedron duoprisms. All except the ''grand antiprism prism'' are based on Wythoff constructions, reflection symmetry generated with Coxeter groups.Symmetry of uniform 5-polytopes in four dimensions
The5-simplex
In five-dimensional geometry, a 5-simplex is a self-dual regular 5-polytope. It has six vertices, 15 edges, 20 triangle faces, 15 tetrahedral cells, and 6 5-cell facets. It has a dihedral angle of cos−1(), or approximately 78.46°.
The 5-s ...
is the regular form in the A5 family. The 5-cube
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.
It is represented by Schläfli symbol or , constructed as 3 tesseracts, ...
and 5-orthoplex
In five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell 4-faces.
It has two constructed forms, the first being regular with ...
are the regular forms in the B5 family. The bifurcating graph of the D5 family contains the 5-orthoplex
In five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell 4-faces.
It has two constructed forms, the first being regular with ...
, as well as a 5-demicube
In five-dimensional geometry, a demipenteract or 5-demicube is a semiregular 5-polytope, constructed from a ''5-hypercube'' (penteract) with alternated vertices removed.
It was discovered by Thorold Gosset. Since it was the only semiregular 5- ...
which is an alternated 5-cube
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.
It is represented by Schläfli symbol or , constructed as 3 tesseracts, ...
.
Each reflective uniform 5-polytope can be constructed in one or more reflective point group in 5 dimensions by a Wythoff construction, represented by rings around permutations of nodes in a Coxeter diagram. Mirror hyperplane
In geometry, a hyperplane is a subspace whose dimension is one less than that of its ''ambient space''. For example, if a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyper ...
s can be grouped, as seen by colored nodes, separated by even-branches. Symmetry groups of the form ,b,b,a have an extended symmetry,  ;Fundamental families
;Uniform prisms
There are 5 finite categorical uniform prismatic families of polytopes based on the nonprismatic uniform 4-polytopes. There is one infinite family of 5-polytopes based on prisms of the uniform duoprisms ××.
;Uniform duoprisms
There are 3 categorical uniform duoprismatic families of polytopes based on
;Fundamental families
;Uniform prisms
There are 5 finite categorical uniform prismatic families of polytopes based on the nonprismatic uniform 4-polytopes. There is one infinite family of 5-polytopes based on prisms of the uniform duoprisms ××.
;Uniform duoprisms
There are 3 categorical uniform duoprismatic families of polytopes based on Cartesian product
In mathematics, specifically set theory, the Cartesian product of two sets ''A'' and ''B'', denoted ''A''×''B'', is the set of all ordered pairs where ''a'' is in ''A'' and ''b'' is in ''B''. In terms of set-builder notation, that is
: A\ti ...
s of the uniform polyhedra and regular polygons: ×.
Enumerating the convex uniform 5-polytopes
*Simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. ...
family: A5 4** 19 uniform 5-polytopes
* Hypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square () and a cube (). It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, ...
/ Orthoplex family: B5 ,33** 31 uniform 5-polytopes
* Demihypercube D5/E5 family: 2,1,1** 23 uniform 5-polytopes (8 unique)
* Polychoral prisms:
** 56 uniform 5-polytope (45 unique) constructions based on prismatic families: ,3,3� nbsp; ,3,3� nbsp; ,3,3� nbsp; 1,1,1� nbsp;
** One non-Wythoffian - The grand antiprism prism
Grand may refer to:
People with the name
* Grand (surname)
* Grand L. Bush (born 1955), American actor
* Grand Mixer DXT, American turntablist
* Grand Puba (born 1966), American rapper
Places
* Grand, Oklahoma
* Grand, Vosges, village and commun ...
is the only known non-Wythoffian convex uniform 5-polytope, constructed from two grand antiprisms connected by polyhedral prisms.
That brings the tally to: 19+31+8+45+1=104
In addition there are:
* Infinitely many uniform 5-polytope constructions based on duoprism prismatic families: 'p''� 'q''� nbsp;
* Infinitely many uniform 5-polytope constructions based on duoprismatic families: ,3� 'p'' ,3� 'p'' ,3� 'p''
The A5 family
There are 19 forms based on all permutations of the Coxeter diagrams with one or more rings. (16+4-1 cases) They are named by Norman Johnson from the Wythoff construction operations upon regular 5-simplex (hexateron). The A5 family has symmetry of order 720 (6factorial
In mathematics, the factorial of a non-negative denoted is the product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times (n-1) \times (n-2) \t ...
). 7 of the 19 figures, with symmetrically ringed Coxeter diagrams have doubled symmetry, order 1440.
The coordinates of uniform 5-polytopes with 5-simplex symmetry can be generated as permutations of simple integers in 6-space, all in hyperplanes with normal vector (1,1,1,1,1,1).
The B5 family
The B5 family has symmetry of order 3840 (5!×25). This family has 25−1=31 Wythoffian uniform polytopes generated by marking one or more nodes of the Coxeter diagram. Also added are 8 uniform polytopes generated as alternations with half the symmetry, which form a complete duplicate of the D5 family as ... = ..... (There are more alternations that are not listed because they produce only repetitions, as ... = .... and ... = .... These would give a complete duplication of the uniform 5-polytopes numbered 20 through 34 with symmetry broken in half.) For simplicity it is divided into two subgroups, each with 12 forms, and 7 "middle" forms which equally belong in both. The 5-cube family of 5-polytopes are given by the convex hulls of the base points listed in the following table, with all permutations of coordinates and sign taken. Each base point generates a distinct uniform 5-polytope. All coordinates correspond with uniform 5-polytopes of edge length 2. {, class="wikitable" !rowspan=2, # !rowspan=2, Base point !rowspan=2, NameCoxeter diagram !colspan=5, Element counts !rowspan=2, Vertex
figure !colspan=6 , Facet counts by location: ,3,3,3, - BGCOLOR="#e0e0f0" !4, , 3, , 2, , 1, , 0 !
,3,3BR>(10) !
,3,2BR>(40) !
,2,3BR>(80) !
,3,3BR>(80) !
,3,3BR>(32) ! Alt , - BGCOLOR="#f0e0e0" !20 , , (0,0,0,0,1)√2, ,
5-orthoplex
In five-dimensional geometry, a 5-orthoplex, or 5-cross polytope, is a five-dimensional polytope with 10 vertices, 40 edges, 80 triangle faces, 80 tetrahedron cells, 32 5-cell 4-faces.
It has two constructed forms, the first being regular with ...
triacontaditeron (tac)
, , 32, , 80, , 80, , 40, , 10 , ,

{3,3,4}, , - , , - , , - , , - , ,

{3,3,3}, , , - BGCOLOR="#f0e0e0" !21 , , (0,0,0,1,1)√2, , Rectified 5-orthoplex
rectified triacontaditeron (rat)
, , 42, , 240, , 400, , 240, , 40 , ,

{ }×{3,4}, ,

{3,3,4} , , - , , - , , - , ,

r{3,3,3} , , , - BGCOLOR="#f0e0e0" !22 , , (0,0,0,1,2)√2, , Truncated 5-orthoplex
truncated triacontaditeron (tot)
, , 42, , 240, , 400, , 280, , 80 , ,

(Octah.pyr), ,

{3,3,4} , , - , , - , , - , ,

t{3,3,3}, , , - BGCOLOR="#e0f0e0" !23 , , (0,0,1,1,1)√2, , Birectified 5-cube
penteractitriacontaditeron (nit)
(Birectified 5-orthoplex)
, , 42, , 280, , 640, , 480, , 80 , ,

{4}×{3}, ,

r{3,3,4} , , - , , - , , - , ,

r{3,3,3} , , , -BGCOLOR="#f0e0e0" !24 , , (0,0,1,1,2)√2, , Cantellated 5-orthoplex
small rhombated triacontaditeron (sart)
, , 82, , 640, , 1520, , 1200, , 240 , ,

Prism-wedge, ,

r{3,3,4}, ,

{ }×{3,4} , , - , , - , ,

rr{3,3,3} , , , - BGCOLOR="#f0e0e0" !25 , , (0,0,1,2,2)√2, , Bitruncated 5-orthoplex
bitruncated triacontaditeron (bittit)
, , 42, , 280, , 720, , 720, , 240 , ,
 , ,
, , 
t{3,3,4} , , - , , - , , - , ,

2t{3,3,3} , , , - BGCOLOR="#f0e0e0" !26 , , (0,0,1,2,3)√2, ,
Cantitruncated 5-orthoplex
In five-dimensional geometry, a cantellated 5-orthoplex is a convex uniform 5-polytope, being a cantellation of the regular 5-orthoplex.
There are 6 cantellation for the 5-orthoplex, including truncations. Some of them are more easily constructe ...
great rhombated triacontaditeron (gart)
, , 82, , 640, , 1520, , 1440, , 480 , ,
 , ,
, , 
t{3,3,4}, ,

{ }×{3,4} , , -, , - , ,

t0,1,3{3,3,3} , , , - BGCOLOR="#e0e0f0" !27 , , (0,1,1,1,1)√2, ,
Rectified 5-cube
In five-dimensional geometry, a rectified 5-cube is a convex uniform 5-polytope, being a rectification of the regular 5-cube.
There are 5 degrees of rectifications of a 5-polytope, the zeroth here being the 5-cube, and the 4th and last being the ...
rectified penteract (rin)
, , 42, , 200, , 400, , 320, , 80 , ,

{3,3}×{ }, ,

r{4,3,3}, , - , , - , , - , ,

{3,3,3} , , , -BGCOLOR="#f0e0e0" !28 , , (0,1,1,1,2)√2, , Runcinated 5-orthoplex
small prismated triacontaditeron (spat)
, , 162, , 1200, , 2160, , 1440, , 320 , ,
 , ,
, , 
r{4,3,3} , ,

{ }×r{3,4} , ,

{3}×{4}, , , ,

t0,3{3,3,3} , , , - BGCOLOR="#e0f0e0" !29 , , (0,1,1,2,2)√2, ,
Bicantellated 5-cube
In six-dimensional geometry, a cantellated 5-cube is a convex uniform 5-polytope, being a cantellation of the regular 5-cube.
There are 6 unique cantellation for the 5-cube, including truncations. Half of them are more easily constructed from th ...
small birhombated penteractitriacontaditeron (sibrant)
(Bicantellated 5-orthoplex)
, , 122, , 840, , 2160, , 1920, , 480 , ,
 , ,
, , 
rr{3,3,4}, , - , ,

{4}×{3}, , - , ,

rr{3,3,3} , , , - BGCOLOR="#f0e0e0" !30 , , (0,1,1,2,3)√2, ,
Runcitruncated 5-orthoplex
In five-dimensional geometry, a runcinated 5-orthoplex is a convex uniform 5-polytope with 3rd order truncation ( runcination) of the regular 5-orthoplex.
There are 8 runcinations of the 5-orthoplex with permutations of truncations, and cantella ...
prismatotruncated triacontaditeron (pattit)
, , 162, , 1440, , 3680, , 3360, , 960 , ,
 , ,
, , 
rr{3,3,4} , ,

{ }×r{3,4} , ,

{6}×{4}, , - , ,

t0,1,3{3,3,3} , , , - BGCOLOR="#e0e0f0" !31 , , (0,1,2,2,2)√2, , Bitruncated 5-cube
bitruncated penteract (bittin)
, , 42, , 280, , 720, , 800, , 320 , ,
 , ,
, , 
2t{4,3,3}, , - , , - , , - , ,

t{3,3,3} , , , - BGCOLOR="#f0e0e0" !32 , , (0,1,2,2,3)√2, , Runcicantellated 5-orthoplex
prismatorhombated triacontaditeron (pirt)
, , 162, , 1200, , 2960, , 2880, , 960 , ,
 , ,
, , 
2t{4,3,3}, ,

{ }×t{3,4}, ,

{3}×{4} , , - , ,

t0,1,3{3,3,3} , , , - BGCOLOR="#e0f0e0" !33 , , (0,1,2,3,3)√2, , Bicantitruncated 5-cube
great birhombated triacontaditeron (gibrant)
(Bicantitruncated 5-orthoplex)
, , 122, , 840, , 2160, , 2400, , 960 , ,
 , ,
, , 
tr{3,3,4}, , - , ,

{4}×{3}, , - , ,

rr{3,3,3} , , , - BGCOLOR="#f0e0e0" !34 , , (0,1,2,3,4)√2, ,
Runcicantitruncated 5-orthoplex
In five-dimensional geometry, a runcinated 5-orthoplex is a convex uniform 5-polytope with 3rd order truncation (runcination) of the regular 5-orthoplex.
There are 8 runcinations of the 5-orthoplex with permutations of truncations, and cantellatio ...
great prismated triacontaditeron (gippit)
, , 162, , 1440, , 4160, , 4800, , 1920 , ,
 , ,
, , 
tr{3,3,4} , ,

{ }×t{3,4} , ,

{6}×{4}, , - , ,

t0,1,2,3{3,3,3} , , , - BGCOLOR="#e0e0f0" !35 , , (1,1,1,1,1), ,
5-cube
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.
It is represented by Schläfli symbol or , constructed as 3 tesseracts, ...
penteract (pent)
, , 10, , 40, , 80, , 80, , 32 , ,

{3,3,3}, ,

{4,3,3}, , - , , - , , - , , - , , , - BGCOLOR="#e0f0e0" !36 , , (1,1,1,1,1)
+ (0,0,0,0,1)√2, , Stericated 5-cube
small cellated penteractitriacontaditeron (scant)
(Stericated 5-orthoplex)
, , 242, , 800, , 1040, , 640, , 160 , ,

Tetr.antiprm, ,

{4,3,3}, ,

{4,3}×{ }, ,

{4}×{3}, ,

{ }×{3,3}, ,

{3,3,3} , , , - BGCOLOR="#e0e0f0" !37 , , (1,1,1,1,1)
+ (0,0,0,1,1)√2, , Runcinated 5-cube
small prismated penteract (span)
, , 202, , 1240, , 2160, , 1440, , 320 , ,
 , ,
, , 
t0,3{4,3,3}, , - , ,

{4}×{3}, ,

{ }×r{3,3}, ,

r{3,3,3} , , , - BGCOLOR="#f0e0e0" !38 , , (1,1,1,1,1)
+ (0,0,0,1,2)√2, , Steritruncated 5-orthoplex
celliprismated triacontaditeron (cappin)
, , 242, , 1520, , 2880, , 2240, , 640 , ,
 , ,
, , 
t0,3{4,3,3} , ,

{4,3}×{ } , ,

{6}×{4} , ,

{ }×t{3,3} , ,

t{3,3,3} , , , - BGCOLOR="#e0e0f0" !39 , , (1,1,1,1,1)
+ (0,0,1,1,1)√2, , Cantellated 5-cube
small rhombated penteract (sirn)
, , 122, , 680, , 1520, , 1280, , 320 , ,

Prism-wedge, ,

rr{4,3,3}, , - , , - , ,

{ }×{3,3}, ,

r{3,3,3} , , , - BGCOLOR="#e0f0e0" !40 , , (1,1,1,1,1)
+ (0,0,1,1,2)√2, ,
Stericantellated 5-cube
In five-dimensional geometry, a stericated 5-cube is a convex uniform 5-polytope with fourth-order truncations ( sterication) of the regular 5-cube.
There are eight degrees of sterication for the 5-cube, including permutations of runcination, can ...
cellirhombated penteractitriacontaditeron (carnit)
(Stericantellated 5-orthoplex)
, , 242, , 2080, , 4720, , 3840, , 960 , ,
 , ,
, , 
rr{4,3,3}, ,

rr{4,3}×{ }, ,

{4}×{3}, ,

{ }×rr{3,3}, ,

rr{3,3,3} , , , - BGCOLOR="#e0e0f0" !41 , , (1,1,1,1,1)
+ (0,0,1,2,2)√2, ,
Runcicantellated 5-cube
In five-dimensional geometry, a runcinated 5-cube is a convex uniform 5-polytope that is a runcination (a 3rd order truncation) of the regular 5-cube.
There are 8 unique degrees of runcinations of the 5-cube, along with permutations of truncations ...
prismatorhombated penteract (prin)
, , 202, , 1240, , 2960, , 2880, , 960 , ,
 , ,
, , 
t0,2,3{4,3,3}, , - , ,

{4}×{3}, ,

{ }×t{3,3}, ,

2t{3,3,3} , , , - BGCOLOR="#f0e0e0" !42 , , (1,1,1,1,1)
+ (0,0,1,2,3)√2, , Stericantitruncated 5-orthoplex
celligreatorhombated triacontaditeron (cogart)
, , 242, , 2320, , 5920, , 5760, , 1920 , ,
 , ,
, , 
t0,2,3{4,3,3}, ,

rr{4,3}×{ }, ,

{6}×{4}, ,

{ }×tr{3,3}, ,

tr{3,3,3} , , , - BGCOLOR="#e0e0f0" !43 , , (1,1,1,1,1)
+ (0,1,1,1,1)√2, ,
Truncated 5-cube
In five-dimensional geometry, a truncated 5-cube is a convex uniform 5-polytope, being a truncation of the regular 5-cube.
There are four unique truncations of the 5-cube. Vertices of the truncated 5-cube are located as pairs on the edge of the 5 ...
truncated penteract (tan)
, , 42, , 200, , 400, , 400, , 160 , ,

Tetrah.pyr, ,

t{4,3,3}, , - , , - , , - , ,

{3,3,3} , , , - BGCOLOR="#e0e0f0" !44 , , (1,1,1,1,1)
+ (0,1,1,1,2)√2, , Steritruncated 5-cube
celliprismated triacontaditeron (capt)
, , 242, , 1600, , 2960, , 2240, , 640 , ,
 , ,
, , 
t{4,3,3}, ,

t{4,3}×{ }, ,

{8}×{3}, ,

{ }×{3,3}, ,

t0,3{3,3,3} , , , - BGCOLOR="#e0e0f0" !45 , , (1,1,1,1,1)
+ (0,1,1,2,2)√2, ,
Runcitruncated 5-cube
In five-dimensional geometry, a runcinated 5-cube is a convex uniform 5-polytope that is a runcination (a 3rd order truncation) of the regular 5-cube.
There are 8 unique degrees of runcinations of the 5-cube, along with permutations of truncatio ...
prismatotruncated penteract (pattin)
, , 202, , 1560, , 3760, , 3360, , 960 , ,
 , ,
, , 
t0,1,3{4,3,3} , , - , ,

{8}×{3}, ,

{ }×r{3,3} , ,

rr{3,3,3} , , , - BGCOLOR="#e0f0e0" !46 , , (1,1,1,1,1)
+ (0,1,1,2,3)√2, , Steriruncitruncated 5-cube
celliprismatotruncated penteractitriacontaditeron (captint)
(Steriruncitruncated 5-orthoplex)
, , 242, , 2160, , 5760, , 5760, , 1920 , ,
 , ,
, , 
t0,1,3{4,3,3}, ,

t{4,3}×{ }, ,

{8}×{6}, ,

{ }×t{3,3}, ,

t0,1,3{3,3,3} , , , - BGCOLOR="#e0e0f0" !47 , , (1,1,1,1,1)
+ (0,1,2,2,2)√2, , Cantitruncated 5-cube
great rhombated penteract (girn)
, , 122, , 680, , 1520, , 1600, , 640 , ,
 , ,
, , 
tr{4,3,3}, , - , , - , ,

{ }×{3,3}, ,

t{3,3,3} , , , - BGCOLOR="#e0e0f0" !48 , , (1,1,1,1,1)
+ (0,1,2,2,3)√2, ,
Stericantitruncated 5-cube
In five-dimensional geometry, a stericated 5-cube is a convex uniform 5-polytope with fourth-order truncations (sterication) of the regular 5-cube.
There are eight degrees of sterication for the 5-cube, including permutations of runcination, cant ...
celligreatorhombated penteract (cogrin)
, , 242, , 2400, , 6000, , 5760, , 1920 , ,
 , ,
, , 
tr{4,3,3}, ,

tr{4,3}×{ }, ,

{8}×{3}, ,

{ }×rr{3,3}, ,

t0,1,3{3,3,3} , , , - BGCOLOR="#e0e0f0" !49 , , (1,1,1,1,1)
+ (0,1,2,3,3)√2, ,
Runcicantitruncated 5-cube
In five-dimensional geometry, a runcinated 5-cube is a convex uniform 5-polytope that is a runcination (a 3rd order truncation) of the regular 5-cube.
There are 8 unique degrees of runcinations of the 5-cube, along with permutations of truncatio ...
great prismated penteract (gippin)
, , 202, , 1560, , 4240, , 4800, , 1920 , ,
 , ,
, , 
t0,1,2,3{4,3,3}, , - , ,

{8}×{3}, ,

{ }×t{3,3}, ,

tr{3,3,3} , , , - BGCOLOR="#e0f0e0" !50 , , (1,1,1,1,1)
+ (0,1,2,3,4)√2, ,
Omnitruncated 5-cube
In five-dimensional geometry, a stericated 5-cube is a convex uniform 5-polytope with fourth-order truncations ( sterication) of the regular 5-cube.
There are eight degrees of sterication for the 5-cube, including permutations of runcination, ...
great cellated penteractitriacontaditeron (gacnet)
(omnitruncated 5-orthoplex)
, , 242, , 2640, , 8160, , 9600, , 3840 , ,

Irr. {3,3,3}, ,

tr{4,3}×{ }, ,

tr{4,3}×{ }, ,

{8}×{6}, ,

{ }×tr{3,3}, ,

t0,1,2,3{3,3,3} , , , - BGCOLOR="#d0f0f0" !51 , ,
5-demicube
In five-dimensional geometry, a demipenteract or 5-demicube is a semiregular 5-polytope, constructed from a ''5-hypercube'' (penteract) with alternated vertices removed.
It was discovered by Thorold Gosset. Since it was the only semiregular 5- ...
hemipenteract (hin)
= , 26 , 120 , 160 , 80 , 16 ,

r{3,3,3} ,

h{4,3,3} , - , - , - , - , (16)

{3,3,3} , - BGCOLOR="#d0f0f0" !52 , , Cantic 5-cube
Truncated hemipenteract (thin)
= , 42 , 280 , 640 , 560 , 160 ,
 ,
, 
h2{4,3,3} , - , - , - , (16)

r{3,3,3} , (16)

t{3,3,3} , - BGCOLOR="#d0f0f0" !53 , ,
Runcic 5-cube
In six-dimensional geometry, a runcic 5-cube or (runcic 5-demicube, runcihalf 5-cube) is a convex uniform 5-polytope. There are 2 runcic forms for the 5-cube. Runcic 5-cubes have half the vertices of runcinated 5-cubes.
Runcic 5-cube
Alterna ...
Small rhombated hemipenteract (sirhin)
= , 42 , 360 , 880 , 720 , 160 , ,

h3{4,3,3} , - , - , - , (16)

r{3,3,3} , (16)

rr{3,3,3} , - BGCOLOR="#d0f0f0" !54 , , Steric 5-cube
Small prismated hemipenteract (siphin)
= , 82 , 480 , 720 , 400 , 80 , ,

h{4,3,3} ,

h{4,3}×{} , - , - , (16)

{3,3,3} , (16)

t0,3{3,3,3} , - BGCOLOR="#d0f0f0" !55 , ,
Runcicantic 5-cube
In six-dimensional geometry, a runcic 5-cube or (runcic 5-demicube, runcihalf 5-cube) is a convex uniform 5-polytope. There are 2 runcic forms for the 5-cube. Runcic 5-cubes have half the vertices of runcinated 5-cubes.
Runcic 5-cube
Alterna ...
Great rhombated hemipenteract (girhin)
= , 42 , 360 , 1040 , 1200 , 480 , ,

h2,3{4,3,3} , - , - , - , (16)

2t{3,3,3} , (16)

tr{3,3,3} , - BGCOLOR="#d0f0f0" !56 , ,
Stericantic 5-cube
In five-dimensional geometry, a steric 5-cube or (steric 5-demicube or sterihalf 5-cube) is a convex uniform 5-polytope. There are unique 4 steric forms of the 5-cube. Steric 5-cubes have half the vertices of stericated 5-cubes.
Steric 5-cub ...
Prismatotruncated hemipenteract (pithin)
= , 82 , 720 , 1840 , 1680 , 480 , ,

h2{4,3,3} ,

h2{4,3}×{} , - , - , (16)

rr{3,3,3} , (16)

t0,1,3{3,3,3} , - BGCOLOR="#d0f0f0" !57 , ,
Steriruncic 5-cube
In five-dimensional geometry, a steric 5-cube or (steric 5-demicube or sterihalf 5-cube) is a convex uniform 5-polytope. There are unique 4 steric forms of the 5-cube. Steric 5-cubes have half the vertices of stericated 5-cubes.
Steric 5-cube ...
Prismatorhombated hemipenteract (pirhin)
= , 82 , 560 , 1280 , 1120 , 320 , ,

h3{4,3,3} ,

h{4,3}×{} , - , - , (16)

t{3,3,3} , (16)

t0,1,3{3,3,3} , - BGCOLOR="#d0f0f0" !58 , ,
Steriruncicantic 5-cube
In five-dimensional geometry, a steric 5-cube or (steric 5-demicube or sterihalf 5-cube) is a convex uniform 5-polytope. There are unique 4 steric forms of the 5-cube. Steric 5-cubes have half the vertices of stericated 5-cubes.
Steric 5-cube ...
Great prismated hemipenteract (giphin)
= , 82 , 720 , 2080 , 2400 , 960 , ,

h2,3{4,3,3} ,

h2{4,3}×{} , - , - , (16)

tr{3,3,3} , (16)

t0,1,2,3{3,3,3} , - BGCOLOR="#d0f0f0" !Nonuniform , , Alternated runcicantitruncated 5-orthoplex
Snub prismatotriacontaditeron (snippit)
Snub hemipenteract (snahin)
= , 1122 , 6240 , 10880 , 6720 , 960 , ,

sr{3,3,4} , sr{2,3,4} , sr{3,2,4} , - , ht0,1,2,3{3,3,3} , (960)

Irr. {3,3,3} , - BGCOLOR="#d0f0f0" !Nonuniform , , Edge-snub 5-orthoplex
Pyritosnub penteract (pysnan)
, 1202 , 7920 , 15360 , 10560 , 1920 , , sr3{3,3,4} , sr3{2,3,4} , sr3{3,2,4} ,

s{3,3}×{ } , ht0,1,2,3{3,3,3} , (960)

Irr. {3,3}×{ } , - BGCOLOR="#d0f0f0" !Nonuniform , , Snub 5-cube
Snub penteract (snan)
, 2162 , 12240 , 21600 , 13440 , 960 , , ht0,1,2,3{3,3,4} , ht0,1,2,3{2,3,4} , ht0,1,2,3{3,2,4} , ht0,1,2,3{3,3,2} , ht0,1,2,3{3,3,3} , (1920)

Irr. {3,3,3}
The D5 family
The D5 family has symmetry of order 1920 (5! x 24). This family has 23 Wythoffian uniform polytopes, from ''3×8-1'' permutations of the D5 Coxeter diagram with one or more rings. 15 (2×8-1) are repeated from the B5 family and 8 are unique to this family, though even those 8 duplicate the alternations from the B5 family. In the 15 repeats, both of the nodes terminating the length-1 branches are ringed, so the two kinds of element are identical and the symmetry doubles: the relations are ... = .... and ... = ..., creating a complete duplication of the uniform 5-polytopes 20 through 34 above. The 8 new forms have one such node ringed and one not, with the relation ... = ... duplicating uniform 5-polytopes 51 through 58 above. {, class="wikitable" !rowspan=2, # !rowspan=2, Coxeter diagramSchläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
symbolsJohnson and Bowers names !colspan=5, Element counts !rowspan=2, Vertex
figure !colspan=6 , Facets by location: 1,2,1 , - !4 !3 !2 !1 !0 !
,3,3BR>(16) !
1,1,1BR>(10) !
,3� nbsp;BR>(40) !
nbsp;� � nbsp;BR>(80) !
,3,3BR>(16) ! Alt , - ! 1, =
h{4,3,3,3},
5-demicube
In five-dimensional geometry, a demipenteract or 5-demicube is a semiregular 5-polytope, constructed from a ''5-hypercube'' (penteract) with alternated vertices removed.
It was discovered by Thorold Gosset. Since it was the only semiregular 5- ...
Hemipenteract (hin) , 26 , 120 , 160 , 80 , 16 ,
r{3,3,3} ,
{3,3,3} ,
h{4,3,3} , - , - , - , , - ! 2, =
h2{4,3,3,3}, cantic 5-cube
Truncated hemipenteract (thin) , 42 , 280 , 640 , 560 , 160 , ,
t{3,3,3} ,
h2{4,3,3} , - , - ,
r{3,3,3} , , - ! 3, =
h3{4,3,3,3},
runcic 5-cube
In six-dimensional geometry, a runcic 5-cube or (runcic 5-demicube, runcihalf 5-cube) is a convex uniform 5-polytope. There are 2 runcic forms for the 5-cube. Runcic 5-cubes have half the vertices of runcinated 5-cubes.
Runcic 5-cube
Alterna ...
Small rhombated hemipenteract (sirhin) , 42 , 360 , 880 , 720 , 160 , ,
rr{3,3,3} ,
h3{4,3,3} , - , - ,
r{3,3,3} , , - ! 4, =
h4{4,3,3,3}, steric 5-cube
Small prismated hemipenteract (siphin) , 82 , 480 , 720 , 400 , 80 , ,
t0,3{3,3,3} ,
h{4,3,3} ,
h{4,3}×{} , - ,
{3,3,3} , , - ! 5, =
h2,3{4,3,3,3},
runcicantic 5-cube
In six-dimensional geometry, a runcic 5-cube or (runcic 5-demicube, runcihalf 5-cube) is a convex uniform 5-polytope. There are 2 runcic forms for the 5-cube. Runcic 5-cubes have half the vertices of runcinated 5-cubes.
Runcic 5-cube
Alterna ...
Great rhombated hemipenteract (girhin) , 42 , 360 , 1040 , 1200 , 480 , ,
2t{3,3,3} ,
h2,3{4,3,3} , - , - ,
tr{3,3,3} , , - ! 6, =
h2,4{4,3,3,3},
stericantic 5-cube
In five-dimensional geometry, a steric 5-cube or (steric 5-demicube or sterihalf 5-cube) is a convex uniform 5-polytope. There are unique 4 steric forms of the 5-cube. Steric 5-cubes have half the vertices of stericated 5-cubes.
Steric 5-cub ...
Prismatotruncated hemipenteract (pithin) , 82 , 720 , 1840 , 1680 , 480 , ,
t0,1,3{3,3,3} ,
h2{4,3,3} ,
h2{4,3}×{} , - ,
rr{3,3,3} , , - ! 7, =
h3,4{4,3,3,3},
steriruncic 5-cube
In five-dimensional geometry, a steric 5-cube or (steric 5-demicube or sterihalf 5-cube) is a convex uniform 5-polytope. There are unique 4 steric forms of the 5-cube. Steric 5-cubes have half the vertices of stericated 5-cubes.
Steric 5-cube ...
Prismatorhombated hemipenteract (pirhin) , 82 , 560 , 1280 , 1120 , 320 , ,
t0,1,3{3,3,3} ,
h3{4,3,3} ,
h{4,3}×{} , - ,
t{3,3,3} , , - ! 8, =
h2,3,4{4,3,3,3},
steriruncicantic 5-cube
In five-dimensional geometry, a steric 5-cube or (steric 5-demicube or sterihalf 5-cube) is a convex uniform 5-polytope. There are unique 4 steric forms of the 5-cube. Steric 5-cubes have half the vertices of stericated 5-cubes.
Steric 5-cube ...
Great prismated hemipenteract (giphin) , 82 , 720 , 2080 , 2400 , 960 , ,
t0,1,2,3{3,3,3} ,
h2,3{4,3,3} ,
h2{4,3}×{} , - ,
tr{3,3,3} , , - bgcolor="#D0F0F0" ! Nonuniform , =
ht0,1,2,3{3,3,3,4}, alternated runcicantitruncated 5-orthoplex
Snub hemipenteract (snahin) , 1122 , 6240 , 10880 , 6720 , 960 , , ht0,1,2,3{3,3,3} ,
sr{3,3,4} , sr{2,3,4} , sr{3,2,4} , ht0,1,2,3{3,3,3} , (960)
Irr. {3,3,3}
Uniform prismatic forms
There are 5 finite categorical uniform prismatic families of polytopes based on the nonprismatic uniform4-polytope
In geometry, a 4-polytope (sometimes also called a polychoron, polycell, or polyhedroid) is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), an ...
s. For simplicity, most alternations are not shown.
A4 × A1
This prismatic family has 9 forms: The A1 x A4 family has symmetry of order 240 (2*5!). {, class="wikitable" !rowspan=2, # !rowspan=2, Coxeter diagramand Schläfli
symbols
Name !colspan=5 rowspan=1, Element counts , - ! Facets, , Cells, , Faces, , Edges, , Vertices , - , 59 , = {3,3,3}×{ }
5-cell prism
In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope Facet (geometry), facets.
The complete set of convex uniform 5-polytopes ...
(penp)
, 7, , 20, , 30, , 25, , 10
, -
, 60
, = r{3,3,3}×{ }Rectified 5-cell prism
Rectification has the following technical meanings:
Mathematics
* Rectification (geometry), truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points
* Rectifiable curve, in mathematics
* Recti ...
(rappip)
, 12, , 50, , 90, , 70, , 20
, -
, 61
, = t{3,3,3}×{ }Truncated 5-cell prism
Truncation is the term used for limiting the number of digits right of the decimal point by discarding the least significant ones.
Truncation may also refer to:
Mathematics
* Truncation (statistics) refers to measurements which have been cut o ...
(tippip)
, 12, , 50, , 100, , 100, , 40
, -
, 62
, = rr{3,3,3}×{ }Cantellated 5-cell prism (srippip) , 22, , 120, , 250, , 210, , 60 , - BGCOLOR="#e0f0e0" , 63 , = t0,3{3,3,3}×{ }
Runcinated 5-cell prism
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers.
It is a higher order truncatio ...
(spiddip)
, 32, , 130, , 200, , 140, , 40
, - BGCOLOR="#e0f0e0"
, 64
, = 2t{3,3,3}×{ }Bitruncated 5-cell prism
In geometry, a bitruncation is an operation on regular polytopes. It represents a truncation beyond rectification. The original edges are lost completely and the original faces remain as smaller copies of themselves.
Bitruncated regular poly ...
(decap)
, 12, , 60, , 140, , 150, , 60
, -
, 65
, = tr{3,3,3}×{ }Cantitruncated 5-cell prism (grippip) , 22, , 120, , 280, , 300, , 120 , - , 66 , = t0,1,3{3,3,3}×{ }
Runcitruncated 5-cell prism (prippip) , 32, , 180, , 390, , 360, , 120 , - BGCOLOR="#e0f0e0" , 67 , = t0,1,2,3{3,3,3}×{ }
Omnitruncated 5-cell prism (gippiddip) , 32, , 210, , 540, , 600, , 240
B4 × A1
This prismatic family has 16 forms. (Three are shared with ,4,3� nbsp;family) The A1×B4 family has symmetry of order 768 (254!). The last three snubs can be realised with equal-length edges, but turn out nonuniform anyway because some of their 4-faces are not uniform 4-polytopes. {, class="wikitable" !rowspan=2, # !rowspan=2, Coxeter diagramand Schläfli
symbols
Name !colspan=5 rowspan=1, Element counts , - ! Facets, , Cells, , Faces, , Edges, , Vertices , - BGCOLOR="#f0e0e0" , 6'', , = {4,3,3}×{ }
Tesseractic prism (pent)
(Same as
5-cube
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.
It is represented by Schläfli symbol or , constructed as 3 tesseracts, ...
)
, 10, , 40, , 80, , 80, , 32
, - BGCOLOR="#f0e0e0"
, 68, , = r{4,3,3}×{ }Rectified tesseractic prism
Rectification has the following technical meanings:
Mathematics
* Rectification (geometry), truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points
* Rectifiable curve, in mathematics
* Recti ...
(rittip)
, 26, , 136, , 272, , 224, , 64
, - BGCOLOR="#f0e0e0"
, 69, , = t{4,3,3}×{ }Truncated tesseractic prism
Truncation is the term used for limiting the number of digits right of the decimal point by discarding the least significant ones.
Truncation may also refer to:
Mathematics
* Truncation (statistics) refers to measurements which have been cut of ...
(tattip)
, 26, , 136, , 304, , 320, , 128
, - BGCOLOR="#f0e0e0"
, 70, , = rr{4,3,3}×{ }Cantellated tesseractic prism (srittip) , 58, , 360, , 784, , 672, , 192 , - BGCOLOR="#e0f0e0" , 71, , = t0,3{4,3,3}×{ }
Runcinated tesseractic prism (sidpithip) , 82, , 368, , 608, , 448, , 128 , - BGCOLOR="#e0f0e0" , 72, , = 2t{4,3,3}×{ }
Bitruncated tesseractic prism (tahp) , 26, , 168, , 432, , 480, , 192 , - BGCOLOR="#f0e0e0" , 73, , = tr{4,3,3}×{ }
Cantitruncated tesseractic prism (grittip) , 58, , 360, , 880, , 960, , 384 , - BGCOLOR="#f0e0e0" , 74, , = t0,1,3{4,3,3}×{ }
Runcitruncated tesseractic prism (prohp) , 82, , 528, , 1216, , 1152, , 384 , - BGCOLOR="#e0f0e0" , 75, , = t0,1,2,3{4,3,3}×{ }
Omnitruncated tesseractic prism
In geometry, an omnitruncation is an operation applied to a regular polytope (or honeycomb) in a Wythoff construction that creates a maximum number of facets. It is represented in a Coxeter–Dynkin diagram with all nodes ringed.
It is a ''sh ...
(gidpithip)
, 82, , 624, , 1696, , 1920, , 768
, - BGCOLOR="#e0e0f0"
, 76, , = {3,3,4}×{ }16-cell prism
In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope Facet (geometry), facets.
The complete set of convex uniform 5-polytopes ...
(hexip)
, 18, , 64, , 88, , 56, , 16
, - BGCOLOR="#e0e0f0"
, 77, , = r{3,3,4}×{ }Rectified 16-cell prism (icope)
(Same as 24-cell prism) , 26, , 144, , 288, , 216, , 48 , - BGCOLOR="#e0e0f0" , 78, , = t{3,3,4}×{ }
Truncated 16-cell prism
Truncation is the term used for limiting the number of digits right of the decimal point by discarding the least significant ones.
Truncation may also refer to:
Mathematics
* Truncation (statistics) refers to measurements which have been cut o ...
(thexip)
, 26, , 144, , 312, , 288, , 96
, - BGCOLOR="#e0e0f0"
, 79, , = rr{3,3,4}×{ }Cantellated 16-cell prism (ricope)
(Same as rectified 24-cell prism) , 50, , 336, , 768, , 672, , 192 , - BGCOLOR="#e0e0f0" , 80, , = tr{3,3,4}×{ }
Cantitruncated 16-cell prism (ticope)
(Same as truncated 24-cell prism) , 50, , 336, , 864, , 960, , 384 , - BGCOLOR="#e0e0f0" , 81, , = t0,1,3{3,3,4}×{ }
Runcitruncated 16-cell prism (prittip) , 82, , 528, , 1216, , 1152, , 384 , - BGCOLOR="#a0e0f0" , 82, , = sr{3,3,4}×{ }
snub 24-cell prism
A snub, cut or slight is a refusal to recognise an acquaintance by ignoring them, avoiding them or pretending not to know them. For example, a failure to greet someone may be considered a snub.
In Awards and Lists
For awards, the term "snub" ...
(sadip)
, 146, , 768, , 1392, , 960, , 192
, - BGCOLOR="#a0e0f0"
, Nonuniform, , rectified tesseractic alterprism (rita) , 50, , 288, , 464, , 288, , 64 , - BGCOLOR="#a0e0f0" , Nonuniform, ,
truncated 16-cell alterprism (thexa) , 26, , 168, , 384, , 336, , 96 , - BGCOLOR="#a0e0f0" , Nonuniform, ,
bitruncated tesseractic alterprism (taha) , 50, , 288, , 624, , 576, , 192
F4 × A1
This prismatic family has 10 forms. The A1 x F4 family has symmetry of order 2304 (2*1152). Three polytopes 85, 86 and 89 (green background) have double symmetry3,4,3
In geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, oct ...
2], order 4608. The last one, snub 24-cell prism, (blue background) has +,4,3,2symmetry, order 1152.
{, class="wikitable"
!rowspan=2, #
!rowspan=2, Coxeter diagramand Schläfli
symbols
Name !colspan=5 rowspan=1, Element counts , - ! Facets, , Cells, , Faces, , Edges, , Vertices , - , 7, = {3,4,3}×{ }
24-cell prism (icope) , 26, , 144, , 288, , 216, , 48 , - , 9, = r{3,4,3}×{ }
rectified 24-cell prism (ricope) , 50, , 336, , 768, , 672, , 192 , - , 0, = t{3,4,3}×{ }
truncated 24-cell prism
Truncation is the term used for limiting the number of digits right of the decimal point by discarding the least significant ones.
Truncation may also refer to:
Mathematics
* Truncation (statistics) refers to measurements which have been cut o ...
(ticope)
, 50, , 336, , 864, , 960, , 384
, -
, 83, , = rr{3,4,3}×{ }cantellated 24-cell prism (sricope) , 146, , 1008, , 2304, , 2016, , 576 , - BGCOLOR="#b0f0b0" , 84, , = t0,3{3,4,3}×{ }
runcinated 24-cell prism (spiccup) , 242, , 1152, , 1920, , 1296, , 288 , - BGCOLOR="#b0f0b0" , 85, , = 2t{3,4,3}×{ }
bitruncated 24-cell prism (contip) , 50, , 432, , 1248, , 1440, , 576 , - , 86, , = tr{3,4,3}×{ }
cantitruncated 24-cell prism (gricope) , 146, , 1008, , 2592, , 2880, , 1152 , - , 87, , = t0,1,3{3,4,3}×{ }
runcitruncated 24-cell prism (pricope) , 242, , 1584, , 3648, , 3456, , 1152 , - BGCOLOR="#b0f0b0" , 88, , = t0,1,2,3{3,4,3}×{ }
omnitruncated 24-cell prism (gippiccup) , 242, , 1872, , 5088, , 5760, , 2304 , - BGCOLOR="#b0e0f0" , 2, = s{3,4,3}×{ }
snub 24-cell prism
A snub, cut or slight is a refusal to recognise an acquaintance by ignoring them, avoiding them or pretending not to know them. For example, a failure to greet someone may be considered a snub.
In Awards and Lists
For awards, the term "snub" ...
(sadip)
, 146, , 768, , 1392, , 960, , 192
H4 × A1
This prismatic family has 15 forms: The A1 x H4 family has symmetry of order 28800 (2*14400). {, class="wikitable" !rowspan=2, # !rowspan=2, Coxeter diagramand Schläfli
symbols
Name !colspan=5 rowspan=1, Element counts , - ! Facets, , Cells, , Faces, , Edges, , Vertices , - BGCOLOR="#f0e0e0" , 89, , = {5,3,3}×{ }
120-cell prism (hipe) , 122, , 960, , 2640, , 3000, , 1200 , - BGCOLOR="#f0e0e0" , 90, , = r{5,3,3}×{ }
Rectified 120-cell prism (rahipe) , 722, , 4560, , 9840, , 8400, , 2400 , - BGCOLOR="#f0e0e0" , 91, , = t{5,3,3}×{ }
Truncated 120-cell prism (thipe) , 722, , 4560, , 11040, , 12000, , 4800 , - BGCOLOR="#f0e0e0" , 92, , = rr{5,3,3}×{ }
Cantellated 120-cell prism (srahip) , 1922, , 12960, , 29040, , 25200, , 7200 , - BGCOLOR="#e0f0e0" , 93, , = t0,3{5,3,3}×{ }
Runcinated 120-cell prism
In geometry, runcination is an operation that cuts a regular polytope (or honeycomb) simultaneously along the faces, edges, and vertices, creating new facets in place of the original face, edge, and vertex centers.
It is a higher order truncatio ...
(sidpixhip)
, 2642, , 12720, , 22080, , 16800, , 4800
, - BGCOLOR="#e0f0e0"
, 94, , = 2t{5,3,3}×{ }Bitruncated 120-cell prism (xhip) , 722, , 5760, , 15840, , 18000, , 7200 , - BGCOLOR="#f0e0e0" , 95, , = tr{5,3,3}×{ }
Cantitruncated 120-cell prism (grahip) , 1922, , 12960, , 32640, , 36000, , 14400 , - BGCOLOR="#f0e0e0" , 96, , = t0,1,3{5,3,3}×{ }
Runcitruncated 120-cell prism (prixip) , 2642, , 18720, , 44880, , 43200, , 14400 , - BGCOLOR="#e0f0e0" , 97, , = t0,1,2,3{5,3,3}×{ }
Omnitruncated 120-cell prism
In geometry, an omnitruncation is an operation applied to a regular polytope (or honeycomb) in a Wythoff construction that creates a maximum number of facets. It is represented in a Coxeter–Dynkin diagram with all nodes ringed.
It is a ''s ...
(gidpixhip)
, 2642, , 22320, , 62880, , 72000, , 28800
, - BGCOLOR="#e0e0f0"
, 98, , = {3,3,5}×{ }600-cell prism
6 (six) is the natural number following 5 and preceding 7. It is a composite number and the smallest perfect number.
In mathematics
Six is the smallest positive integer which is neither a square number nor a prime number; it is the second small ...
(exip)
, 602, , 2400, , 3120, , 1560, , 240
, - BGCOLOR="#e0e0f0"
, 99, , = r{3,3,5}×{ }Rectified 600-cell prism
Rectification has the following technical meanings:
Mathematics
* Rectification (geometry), truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points
* Rectifiable curve, in mathematics
* Recti ...
(roxip)
, 722, , 5040, , 10800, , 7920, , 1440
, - BGCOLOR="#e0e0f0"
, 100, , = t{3,3,5}×{ }Truncated 600-cell prism (texip) , 722, , 5040, , 11520, , 10080, , 2880 , - BGCOLOR="#e0e0f0" , 101, , = rr{3,3,5}×{ }
Cantellated 600-cell prism (srixip) , 1442, , 11520, , 28080, , 25200, , 7200 , - BGCOLOR="#e0e0f0" , 102, , = tr{3,3,5}×{ }
Cantitruncated 600-cell prism (grixip) , 1442, , 11520, , 31680, , 36000, , 14400 , - BGCOLOR="#e0e0f0" , 103, , = t0,1,3{3,3,5}×{ }
Runcitruncated 600-cell prism (prahip) , 2642, , 18720, , 44880, , 43200, , 14400
Duoprism prisms
Uniform duoprism prisms, {''p''}×{''q''}×{ }, form an infinite class for all integers ''p'',''q''>2. {4}×{4}×{ } makes a lower symmetry form of the5-cube
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.
It is represented by Schläfli symbol or , constructed as 3 tesseracts, ...
.
{, class="wikitable"
, -
!rowspan=2, Coxeter diagram
!rowspan=2, Names
!colspan=6, Element counts
, -
! 4-faces
! Cells
! Faces
! Edges
! Vertices
, - align=center
, , , {''p''}×{''q''}×{ }, , ''p''+''q''+2, , 3''pq''+3''p''+3''q'', , 4''pq''+2''p''+2''q'', , 5''pq'', , 2''pq''
, - align=center
, , , {''p''}2×{ }, , 2(''p''+1), , 3''p''(''p''+1), , 4''p''(''p''+1), , 5''p''2, , 2''p''2
, - align=center
, , , {3}2×{ }, , 8, , 36, , 48, , 45, , 18
, - align=center
, , , {4}2×{ } = 5-cube
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.
It is represented by Schläfli symbol or , constructed as 3 tesseracts, ...
, , 10, , 40, , 80, , 80, , 32
Grand antiprism prism
The grand antiprism prism is the only known convex non-Wythoffian uniform 5-polytope. It has 200 vertices, 1100 edges, 1940 faces (40 pentagons, 500 squares, 1400 triangles), 1360 cells (600 tetrahedra, 40 pentagonal antiprisms, 700 triangular prisms, 20 pentagonal prisms), and 322 hypercells (2 grand antiprisms , 20 pentagonal antiprism prisms , and 300 tetrahedral prisms ). {, class="wikitable" !rowspan=2, # !rowspan=2, Name !colspan=5, Element counts , - ! Facets, , Cells, , Faces, , Edges, , Vertices , - , 104, ,grand antiprism prism
Grand may refer to:
People with the name
* Grand (surname)
* Grand L. Bush (born 1955), American actor
* Grand Mixer DXT, American turntablist
* Grand Puba (born 1966), American rapper
Places
* Grand, Oklahoma
* Grand, Vosges, village and commun ...
(gappip), , 322, , 1360, , 1940, , 1100, , 200
Notes on the Wythoff construction for the uniform 5-polytopes
Construction of the reflective 5-dimensional uniform polytopes are done through a Wythoff construction process, and represented through a Coxeter diagram, where each node represents a mirror. Nodes are ringed to imply which mirrors are active. The full set of uniform polytopes generated are based on the unique permutations of ringed nodes. Uniform 5-polytopes are named in relation to the regular polytopes in each family. Some families have two regular constructors and thus may have two ways of naming them. Here are the primary operators available for constructing and naming the uniform 5-polytopes. The last operation, the snub, and more generally the alternation, are the operation that can create nonreflective forms. These are drawn with "hollow rings" at the nodes. The prismatic forms and bifurcating graphs can use the same truncation indexing notation, but require an explicit numbering system on the nodes for clarity. {, class="wikitable" !Operation !width=200 colspan=2, ExtendedSchläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
!width=80, Coxeter diagram
!Description
, - align=center
! Parent
, t0{p,q,r,s}
, {p,q,r,s}
,
, Any regular 5-polytope
, - align=center
! Rectified
, t1{p,q,r,s}, , r{p,q,r,s}
,
, align=left, The edges are fully truncated into single points. The 5-polytope now has the combined faces of the parent and dual.
, - align=center
! Birectified
, t2{p,q,r,s}, , 2r{p,q,r,s}
,
, align=left, Birectification reduces faces to points, cells
Cell most often refers to:
* Cell (biology), the functional basic unit of life
Cell may also refer to:
Locations
* Monastic cell, a small room, hut, or cave in which a religious recluse lives, alternatively the small precursor of a monastery w ...
to their duals.
, - align=center
! Trirectified
, t3{p,q,r,s}, , 3r{p,q,r,s}
,
, align=left, Trirectification reduces cells to points. (Dual rectification)
, - align=center
! Quadrirectified
, t4{p,q,r,s}, , 4r{p,q,r,s}
,
, align=left, Quadrirectification reduces 4-faces to points. (Dual)
, - align=center
! Truncated
, t0,1{p,q,r,s}, , t{p,q,r,s}
,
, align=left, Each original vertex is cut off, with a new face filling the gap. Truncation has a degree of freedom, which has one solution that creates a uniform truncated 5-polytope. The 5-polytope has its original faces doubled in sides, and contains the faces of the dual., - align=center ! Cantellated , t0,2{p,q,r,s}, , rr{p,q,r,s} , , align=left, In addition to vertex truncation, each original edge is ''beveled'' with new rectangular faces appearing in their place.
, - align=center ! Runcinated , colspan=2, t0,3{p,q,r,s} , , align=left, Runcination reduces cells and creates new cells at the vertices and edges. , - align=center ! Stericated , t0,4{p,q,r,s}, , 2r2r{p,q,r,s} , , align=left, Sterication reduces facets and creates new facets (hypercells) at the vertices and edges in the gaps. (Same as expansion operation for 5-polytopes.) , - align=center !
Omnitruncated
In geometry, an omnitruncation is an operation applied to a regular polytope (or honeycomb) in a Wythoff construction that creates a maximum number of facets. It is represented in a Coxeter–Dynkin diagram with all nodes ringed.
It is a ''shortc ...
, colspan=2, t0,1,2,3,4{p,q,r,s}
,
, align=left, All four operators, truncation, cantellation, runcination, and sterication are applied.
, - align=center
!Half
, colspan=2, h{2p,3,q,r}
,
, align=left, Alternation, same as
, - align=center
!Cantic
, colspan=2, h2{2p,3,q,r}
,
, align=left, Same as
, - align=center
!Runcic
, colspan=2, h3{2p,3,q,r}
,
, align=left, Same as
, - align=center
!Runcicantic
, colspan=2, h2,3{2p,3,q,r}
,
, align=left, Same as
, - align=center
!Steric
, colspan=2, h4{2p,3,q,r}
,
, align=left, Same as
, - align=center
!Steriruncic
, colspan=2, h3,4{2p,3,q,r}
,
, align=left, Same as
, - align=center
!Stericantic
, colspan=2, h2,4{2p,3,q,r}
,
, align=left, Same as
, - align=center
!Steriruncicantic
, colspan=2, h2,3,4{2p,3,q,r}
,
, align=left, Same as
, - align=center
!Snub
, colspan=2, s{p,2q,r,s}
,
, align=left, Alternated truncation
, - align=center
!Snub rectified
, colspan=2, sr{p,q,2r,s}
,
, align=left, Alternated truncated rectification
, - align=center
!
, colspan=2, ht0,1,2,3{p,q,r,s}
,
, align=left, Alternated runcicantitruncation
, - align=center
!Full snub
, colspan=2, ht0,1,2,3,4{p,q,r,s}
,
, align=left, Alternated omnitruncation
Regular and uniform honeycombs
There are five fundamental affine Coxeter groups, and 13 prismatic groups that generate regular and uniform tessellations in Euclidean 4-space. {, class=wikitable , + Fundamental groups , - !# !colspan=3, Coxeter group ! Coxeter diagram !Forms , - align=center , 1, , , , [5/sup>">.html" ;"title="[5">[5/sup>">[(3,3,3,3,3)">">, 7 , - align=center , 2, , , , , , , , 19 , - align=center , 3, , , , [4,3,3,4,1+, = , , 23 (8 new) , - align=center , 4, , , , = , , 9 (0 new) , - align=center , 5, , , , , , , , 31 (21 new) There are three regular honeycombs of Euclidean 4-space: * tesseractic honeycomb, with symbols {4,3,3,4}, = . There are 19 uniform honeycombs in this family. * 24-cell honeycomb, with symbols {3,4,3,3}, . There are 31 reflective uniform honeycombs in this family, and one alternated form. ** Truncated 24-cell honeycomb with symbols t{3,4,3,3}, ** Snub 24-cell honeycomb, with symbols s{3,4,3,3}, and constructed by four snub 24-cell, one 16-cell, and five 5-cells at each vertex. *16-cell honeycomb
In Four-dimensional space, four-dimensional Euclidean geometry, the 16-cell honeycomb is one of the three regular space-filling tessellations (or honeycomb (geometry), honeycombs), represented by Schläfli symbol , and constructed by a 4-dimensiona ...
, with symbols {3,3,4,3},
Other families that generate uniform honeycombs:
* There are 23 uniquely ringed forms, 8 new ones in the 16-cell honeycomb
In Four-dimensional space, four-dimensional Euclidean geometry, the 16-cell honeycomb is one of the three regular space-filling tessellations (or honeycomb (geometry), honeycombs), represented by Schläfli symbol , and constructed by a 4-dimensiona ...
family. With symbols h{4,32,4} it is geometrically identical to the 16-cell honeycomb
In Four-dimensional space, four-dimensional Euclidean geometry, the 16-cell honeycomb is one of the three regular space-filling tessellations (or honeycomb (geometry), honeycombs), represented by Schläfli symbol , and constructed by a 4-dimensiona ...
, =
* There are 7 uniquely ringed forms from the , family, all new, including:
** 4-simplex honeycomb
** Truncated 4-simplex honeycomb
In four-dimensional Euclidean geometry, the 4-simplex honeycomb, 5-cell honeycomb or pentachoric-dispentachoric honeycomb is a space-filling tessellation honeycomb. It is composed of 5-cells and rectified 5-cells facets in a ratio of 1:1. Str ...
** Omnitruncated 4-simplex honeycomb
In four-dimensional Euclidean geometry, the 4-simplex honeycomb, 5-cell honeycomb or pentachoric-dispentachoric honeycomb is a space-filling tessellation honeycomb (geometry), honeycomb. It is composed of 5-cells and rectified 5-cells facets in a ...
* There are 9 uniquely ringed forms in the : 1,1,1,1 family, two new ones, including the quarter tesseractic honeycomb, = , and the bitruncated tesseractic honeycomb, = .
Non-Wythoffian uniform tessellations in 4-space also exist by elongation (inserting layers), and gyration (rotating layers) from these reflective forms.
{, class=wikitable
, + Prismatic groups
, -
!#
!colspan=2, Coxeter group
! Coxeter diagram
, -
, 1, , ×, , ,3,4,2,∞,
, -
, 2, , ×, , ,31,1,2,∞,
, -
, 3, , ×, , [4/sup>,2,∞">.html" ;"title="[4">[4/sup>,2,∞">
, -
, 4, , ×x, , [4,4,2,∞,2,∞,
, -
, 5, , ×x, , [6,3,2,∞,2,∞], ,
, -
, 6, , ×x, , [3/sup>,2,∞,2,∞], ,
, -
, 7, , ×xx, , ��,2,∞,2,∞,2,∞,
, -
, 8, , x, , [3/sup>,2,3[3">.html" ;"title="[3">[3/sup>,2,3[3/sup>">"><sup>[3<_a>_sup>,2,3<sup>.html" ;"title=".html" ;"title="[3">[3/sup>,2,3[3">.html" ;"title="[3">[3/sup>,2,3[3/sup>">
, -
, 9, , ×, , [3/sup>,2,4,4">
, -
, 10, , ×, , [3/sup>,2,6,3">
">-
, 11, , ×, ,
, -
, 12, , ×, , [4,4,2,6,3,
, -
, 13, , ×, ,
Regular and uniform hyperbolic honeycombs
;Hyperbolic compact groups There are 5 Coxeter-Dynkin diagram#Compact, compact hyperbolic Coxeter groups of rank 5, each generating uniform honeycombs in hyperbolic 4-space as permutations of rings of the Coxeter diagrams. {, class="wikitable" , valign=top align= = [(3,3,3,3,4)]: , valign=top align= = [5,3,31,1]: , valign=top align= = [3,3,3,5]:= [4,3,3,5]:
= ,3,3,5 There are 5 regular compact convex hyperbolic honeycombs in H4 space:Coxeter, The Beauty of Geometry: Twelve Essays, Chapter 10: Regular honeycombs in hyperbolic space, Summary tables IV p213 {, class="wikitable" , + Compact regular convex hyperbolic honeycombs , - !Honeycomb name ! Schläfli
Symbol
{p,q,r,s} ! Coxeter diagram !Facet
type
{p,q,r} !Cell
type
{p,q} !Face
type
{p} !Face
figure
{s} !Edge
figure
{r,s} ! Vertex
figure
{q,r,s} !
Dual
Dual or Duals may refer to:
Paired/two things
* Dual (mathematics), a notion of paired concepts that mirror one another
** Dual (category theory), a formalization of mathematical duality
*** see more cases in :Duality theories
* Dual (grammatical ...
, - BGCOLOR="#ffe0e0" align=center
, Order-5 5-cell (pente), , {3,3,3,5}, , , , {3,3,3}, , {3,3}, , {3}, , {5}, , {3,5}, , {3,3,5}, , {5,3,3,3}
, - BGCOLOR="#e0e0ff" align=center
, Order-3 120-cell (hitte), , {5,3,3,3}, , , , {5,3,3}, , {5,3}, , {5}, , {3}, , {3,3}, , {3,3,3}, , {3,3,3,5}
, - BGCOLOR="#ffe0e0" align=center
, Order-5 tesseractic (pitest), , {4,3,3,5}, , , , {4,3,3}, , {4,3}, , {4}, , {5}, , {3,5}, , {3,3,5}, , {5,3,3,4}
, - BGCOLOR="#e0e0ff" align=center
, Order-4 120-cell (shitte), , {5,3,3,4}, , , , {5,3,3}, , {5,3}, , {5}, , {4}, , {3,4}, , {3,3,4}, , {4,3,3,5}
, - BGCOLOR="#e0ffe0" align=center
, Order-5 120-cell (phitte), , {5,3,3,5}, , , , {5,3,3}, , {5,3}, , {5}, , {5}, , {3,5}, , {3,3,5}, , Self-dual
There are also 4 regular compact hyperbolic star-honeycombs in H4 space:
{, class="wikitable"
, + Compact regular hyperbolic star-honeycombs
, -
!Honeycomb name
! SchläfliSymbol
{p,q,r,s} ! Coxeter diagram !Facet
type
{p,q,r} !Cell
type
{p,q} !Face
type
{p} !Face
figure
{s} !Edge
figure
{r,s} ! Vertex
figure
{q,r,s} !
Dual
Dual or Duals may refer to:
Paired/two things
* Dual (mathematics), a notion of paired concepts that mirror one another
** Dual (category theory), a formalization of mathematical duality
*** see more cases in :Duality theories
* Dual (grammatical ...
, - BGCOLOR="#ffe0e0" align=center
, Order-3 small stellated 120-cell, , {5/2,5,3,3}, , , , {5/2,5,3}, , {5/2,5}, , {5}, , {5}, , {3,3}, , {5,3,3}, , {3,3,5,5/2}
, - BGCOLOR="#e0e0ff" align=center
, Order-5/2 600-cell, , {3,3,5,5/2}, , , , {3,3,5}, , {3,3}, , {3}, , {5/2}, , {5,5/2}, , {3,5,5/2}, , {5/2,5,3,3}
, - BGCOLOR="#ffe0e0" align=center
, Order-5 icosahedral 120-cell, , {3,5,5/2,5}, , , , {3,5,5/2}, , {3,5}, , {3}, , {5}, , {5/2,5}, , {5,5/2,5}, , {5,5/2,5,3}
, - BGCOLOR="#e0e0ff" align=center
, Order-3 great 120-cell, , {5,5/2,5,3}, , , , {5,5/2,5}, , {5,5/2}, , {5}, , {3}, , {5,3}, , {5/2,5,3}, , {3,5,5/2,5}
;Hyperbolic paracompact groups
There are 9 paracompact hyperbolic Coxeter groups of rank 5, each generating uniform honeycombs in 4-space as permutations of rings of the Coxeter diagrams. Paracompact groups generate honeycombs with infinite facets or vertex figures.
{, class=wikitable
, align=
= ,3[4/sup>">.html" ;"title=",3[4">,3[4/sup>
= [4,3[4">">,3<sup>[4<_a>_sup>.html" ;"title=".html" ;"title=",3[4">,3[4/sup>">.html" ;"title=",3[4">,3[4/sup>
= [4,3[4/sup>]: = [(3,3,4,3,4)]:
= [3 �[]]: , align= = ,/3\,3,4
= ,4,31,1
= ,32,1
= ,31,1,1 , align= = ,4,3,4
Notes
References
* T. Gosset: ''On the Regular and Semi-Regular Figures in Space of n Dimensions'', Messenger of Mathematics, Macmillan, 1900 (3 regular and one semiregular 4-polytope) * A. Boole Stott: ''Geometrical deduction of semiregular from regular polytopes and space fillings'', Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910 *H.S.M. Coxeter
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century.
Biography
Coxeter was born in Kensington t ...
:
** H.S.M. Coxeter
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century.
Biography
Coxeter was born in Kensington t ...
, ''Regular Polytopes'', 3rd Edition, Dover New York, 1973 (p. 297 Fundamental regions for irreducible groups generated by reflections, Spherical and Euclidean)
** H.S.M. Coxeter
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century.
Biography
Coxeter was born in Kensington t ...
, ''The Beauty of Geometry: Twelve Essays'' (Chapter 10: Regular honeycombs in hyperbolic space, Summary tables IV p213)
* Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', ath. Zeit. 46 (1940) 380-407, MR 2,10** (Paper 23) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes II'', ath. Zeit. 188 (1985) 559-591(p. 287 5D Euclidean groups, p. 298 Four-dimensionsal honeycombs) ** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', ath. Zeit. 200 (1988) 3-45* N.W. Johnson: ''The Theory of Uniform Polytopes and Honeycombs'', Ph.D. Dissertation, University of Toronto, 1966 * James E. Humphreys, ''Reflection Groups and Coxeter Groups'', Cambridge studies in advanced mathematics, 29 (1990) (Page 141, 6.9 List of hyperbolic Coxeter groups, figure 2
External links
* – includes nonconvex forms as well as the duplicate constructions from the B5 and D5 families {{Honeycombs 5-polytopes eo:5-hiperpluredro