|
Octahedral Prism
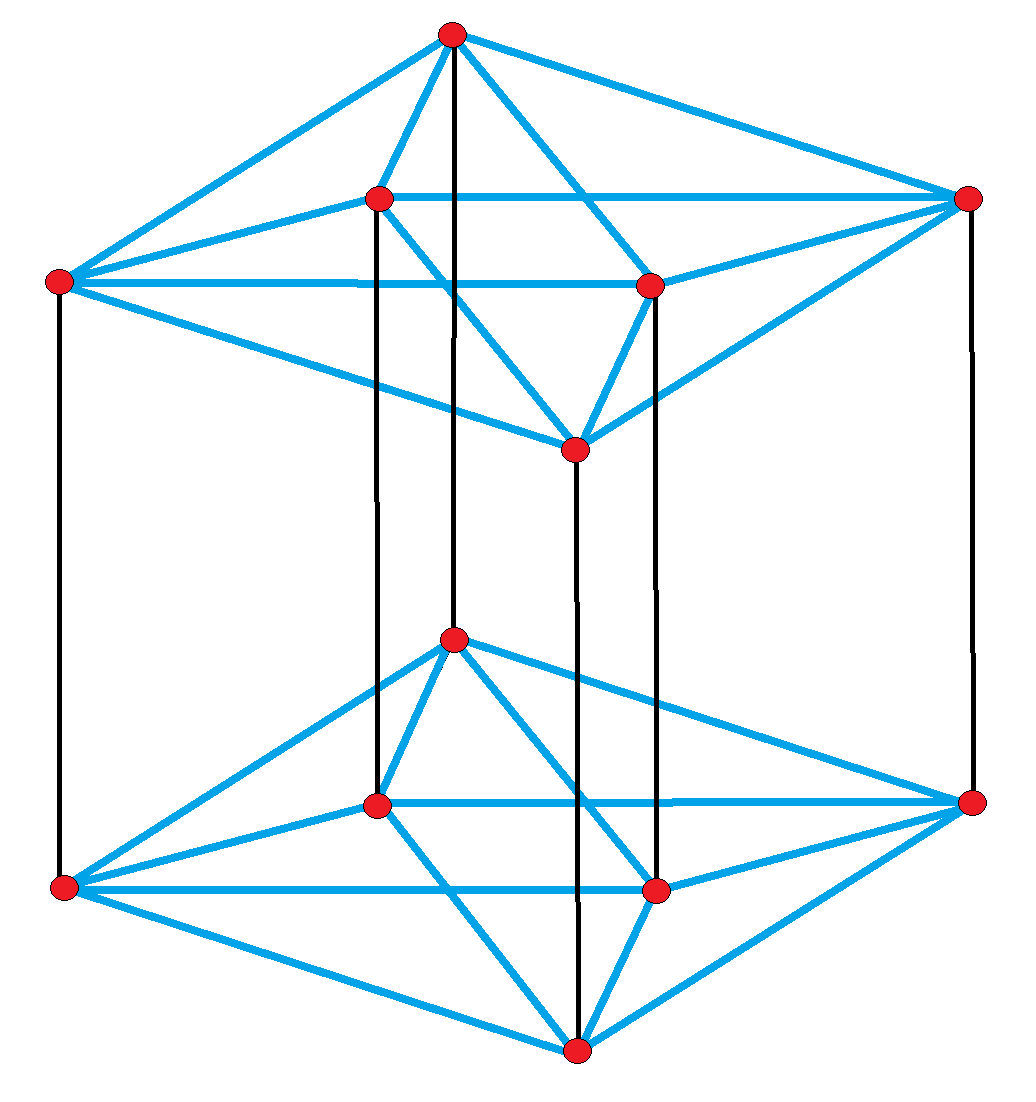
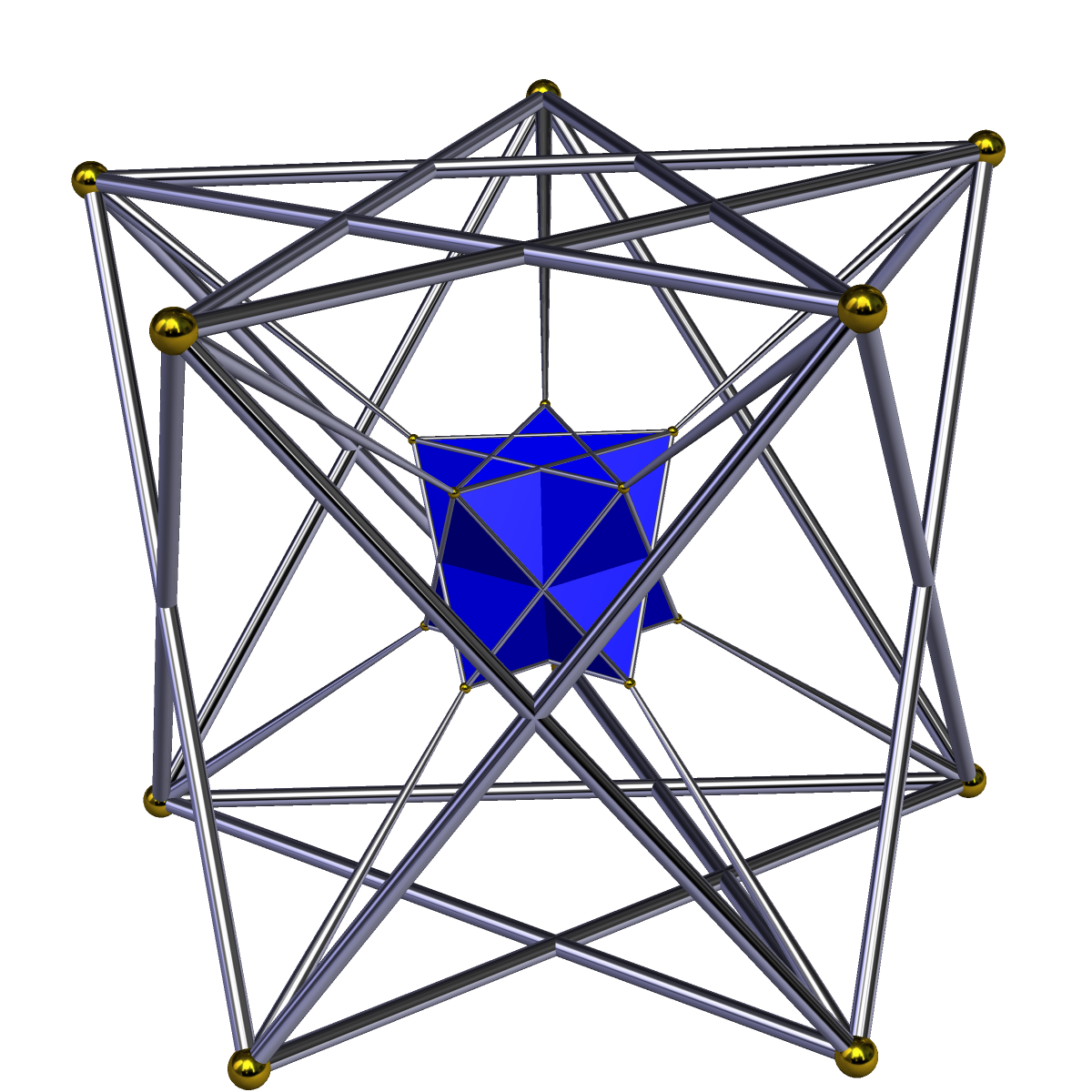
In geometry, an octahedral prism is a convex uniform 4-polytope. This 4-polytope has 10 polyhedral cells: 2 octahedra connected by 8 triangular prisms. Alternative names *Octahedral dyadic prism ( Norman W. Johnson) *Ope (Jonathan Bowers, for octahedral prism) *Triangular antiprismatic prism *Triangular antiprismatic hyperprism Coordinates It is a Hanner polytope with vertex coordinates, permuting first 3 coordinates: :( ±1,0,0 ±1) Structure The octahedral prism consists of two octahedra connected to each other via 8 triangular prisms. The triangular prisms are joined to each other via their square faces. Projections The octahedron-first orthographic projection of the octahedral prism into 3D space has an octahedral envelope. The two octahedral cells project onto the entire volume of this envelope, while the 8 triangular prismic cells project onto its 8 triangular faces. The triangular-prism-first orthographic projection of the octahedral prism into 3D space has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octahedral Prism
In geometry, an octahedral prism is a convex uniform 4-polytope. This 4-polytope has 10 polyhedral cells: 2 octahedra connected by 8 triangular prisms. Alternative names *Octahedral dyadic prism ( Norman W. Johnson) *Ope (Jonathan Bowers, for octahedral prism) *Triangular antiprismatic prism *Triangular antiprismatic hyperprism Coordinates It is a Hanner polytope with vertex coordinates, permuting first 3 coordinates: :( ±1,0,0 ±1) Structure The octahedral prism consists of two octahedra connected to each other via 8 triangular prisms. The triangular prisms are joined to each other via their square faces. Projections The octahedron-first orthographic projection of the octahedral prism into 3D space has an octahedral envelope. The two octahedral cells project onto the entire volume of this envelope, while the 8 triangular prismic cells project onto its 8 triangular faces. The triangular-prism-first orthographic projection of the octahedral prism into 3D space has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the n-dimensional Euclidean space \mathbb^n. Most texts. use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others''Mathematical Programming'', by Melvyn W. Jeter (1986) p. 68/ref> (including this article) allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary. Convex polytopes play an important role both in various branches of mathematics and in applied areas, most notably in linear programming. In the influential textbooks of GrĂĽnbaum and Ziegler on the subject, as well as in many other texts in discrete geometry, convex polytopes are often simply called "polytopes". GrĂĽnbaum points out that this is solely to avoi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Platonic Solid
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all edges congruent), and the same number of faces meet at each vertex. There are only five such polyhedra: Geometers have studied the Platonic solids for thousands of years. They are named for the ancient Greek philosopher Plato who hypothesized in one of his dialogues, the ''Timaeus'', that the classical elements were made of these regular solids. History The Platonic solids have been known since antiquity. It has been suggested that certain carved stone balls created by the late Neolithic people of Scotland represent these shapes; however, these balls have rounded knobs rather than being polyhedral, the numbers of knobs frequently differed from the numbers of vertices of the Platonic solids, there is no ball whose knobs match the 20 vertic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prism (geometry)
In geometry, a prism is a polyhedron comprising an polygon Base (geometry), base, a second base which is a Translation (geometry), translated copy (rigidly moved without rotation) of the first, and other Face (geometry), faces, necessarily all parallelograms, joining corresponding sides of the two bases. All Cross section (geometry), cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids. Like many basic geometric terms, the word ''prism'' () was first used in Euclid's Elements. Euclid defined the term in Book XI as “a solid figure contained by two opposite, equal and parallel planes, while the rest are parallelograms”. However, this definition has been criticized for not being specific enough in relation to the nature of the bases, which caused confusion among later geometry writers. Oblique prism An oblique prism is a pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Antiprismatic Prism
In 4-dimensional geometry, a uniform antiprismatic prism or antiduoprism is a uniform 4-polytope with two uniform antiprism cells in two parallel 3-space hyperplanes, connected by uniform prisms cells between pairs of faces. The symmetry of a ''p''-gonal antiprismatic prism is ''p'',2+,2 order 8''p''. A p-gonal antiprismatic prism or p-gonal antiduoprism has 2 ''p''-gonal antiprism, 2 ''p''-gonal prism, and ''2p'' triangular prism cells. It has 4''p'' equilateral triangle, 4''p'' square and 4 regular ''p''-gon faces. It has 10''p'' edges, and 4''p'' vertices. Convex uniform antiprismatic prisms There is an infinite series of convex uniform antiprismatic prisms, starting with the ''digonal antiprismatic prism'' is a tetrahedral prism, with two of the tetrahedral cells degenerated into squares. The ''triangular antiprismatic prism'' is the first nondegenerate form, which is also an octahedral prism. The remainder are unique uniform 4-polytopes. Star antiprismatic prisms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagonal Prism
In geometry, the hexagonal prism is a prism with hexagonal base. Prisms are polyhedrons; this polyhedron has 8 faces, 18 edges, and 12 vertices.. Since it has 8 faces, it is an octahedron. However, the term ''octahedron'' is primarily used to refer to the ''regular octahedron'', which has eight triangular faces. Because of the ambiguity of the term ''octahedron'' and tilarity of the various eight-sided figures, the term is rarely used without clarification. Before sharpening, many pencils take the shape of a long hexagonal prism. As a semiregular (or uniform) polyhedron If faces are all regular, the hexagonal prism is a semiregular polyhedron, more generally, a uniform polyhedron, and the fourth in an infinite set of prisms formed by square sides and two regular polygon caps. It can be seen as a truncated hexagonal hosohedron, represented by Schläfli symbol t. Alternately it can be seen as the Cartesian product of a regular hexagon and a line segment, and represented by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Envelope (mathematics)
In geometry, an envelope of a planar family of curves is a curve that is tangent to each member of the family at some point, and these points of tangency together form the whole envelope. Classically, a point on the envelope can be thought of as the intersection of two "infinitesimally adjacent" curves, meaning the limit of intersections of nearby curves. This idea can be generalized to an envelope of surfaces in space, and so on to higher dimensions. To have an envelope, it is necessary that the individual members of the family of curves are differentiable curves as the concept of tangency does not apply otherwise, and there has to be a smooth transition proceeding through the members. But these conditions are not sufficient – a given family may fail to have an envelope. A simple example of this is given by a family of concentric circles of expanding radius. Envelope of a family of curves Let each curve ''C''''t'' in the family be given as the solution of an equation ''f'''' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthographic Projection
Orthographic projection (also orthogonal projection and analemma) is a means of representing Three-dimensional space, three-dimensional objects in Two-dimensional space, two dimensions. Orthographic projection is a form of parallel projection in which all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface. The obverse of an orthographic projection is an oblique projection, which is a parallel projection in which the projection lines are ''not'' orthogonal to the projection plane. The term ''orthographic'' sometimes means a technique in multiview projection in which principal axes or the planes of the subject are also parallel with the projection plane to create the ''primary views''. If the principal planes or axes of an object in an orthographic projection are ''not'' parallel with the projection plane, the depiction is called ''axonometric'' or an ''auxiliary views''. (''A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octahedral Hyperprism Schlegel
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. A regular octahedron is the dual polyhedron of a cube. It is a rectified tetrahedron. It is a square bipyramid in any of three orthogonal orientations. It is also a triangular antiprism in any of four orientations. An octahedron is the three-dimensional case of the more general concept of a cross polytope. A regular octahedron is a 3-ball in the Manhattan () metric. Regular octahedron Dimensions If the edge length of a regular octahedron is ''a'', the radius of a circumscribed sphere (one that touches the octahedron at all vertices) is :r_u = \frac a \approx 0.707 \cdot a and the radius of an inscribed sphere (tangent to each of the octahedron's faces) is :r_i = \frac a \approx 0.408\cdot a while the midradius, which tou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Norman Johnson (mathematician)
Norman Woodason Johnson () was a mathematician at Wheaton College, Norton, Massachusetts. Early life and education Norman Johnson was born on in Chicago. His father had a bookstore and published a local newspaper. Johnson earned his undergraduate mathematics degree in 1953 at Carleton College in Northfield, Minnesota followed by a master's degree from the University of Pittsburgh. After graduating in 1953, Johnson did alternative civilian service as a conscientious objector. He earned his PhD from the University of Toronto in 1966 with a dissertation title of ''The Theory of Uniform Polytopes and Honeycombs'' under the supervision of H. S. M. Coxeter. From there, he accepted a position in the Mathematics Department of Wheaton College in Massachusetts and taught until his retirement in 1998. Career In 1966, he enumerated 92 convex non-uniform polyhedra with regular faces. Victor Zalgaller later proved (1969) that Johnson's list was complete, and the set is now known a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedron
In geometry, a polyhedron (plural polyhedra or polyhedrons; ) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices. A convex polyhedron is the convex hull of finitely many points, not all on the same plane. Cubes and pyramids are examples of convex polyhedra. A polyhedron is a 3-dimensional example of a polytope, a more general concept in any number of dimensions. Definition Convex polyhedra are well-defined, with several equivalent standard definitions. However, the formal mathematical definition of polyhedra that are not required to be convex has been problematic. Many definitions of "polyhedron" have been given within particular contexts,. some more rigorous than others, and there is not universal agreement over which of these to choose. Some of these definitions exclude shapes that have often been counted as polyhedra (such as the self-crossing polyhedra) or include shapes that are often not considered as valid polyhedr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform 4-polytope
In geometry, a uniform 4-polytope (or uniform polychoron) is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons. There are 47 non-prismatic convex uniform 4-polytopes. There are two infinite sets of convex prismatic forms, along with 17 cases arising as prisms of the convex uniform polyhedra. There are also an unknown number of non-convex star forms. History of discovery * Convex Regular polytopes: ** 1852: Ludwig Schläfli proved in his manuscript ''Theorie der vielfachen Kontinuität'' that there are exactly 6 regular polytopes in 4 dimensions and only 3 in 5 or more dimensions. * Regular star 4-polytopes (star polyhedron cells and/or vertex figures) ** 1852: Ludwig Schläfli also found 4 of the 10 regular star 4-polytopes, discounting 6 with cells or vertex figures and . ** 1883: Edmund Hess completed the list of 10 of the nonconvex regular 4-polytopes, in his book (in German) ''Einleitung in die Leh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |