|
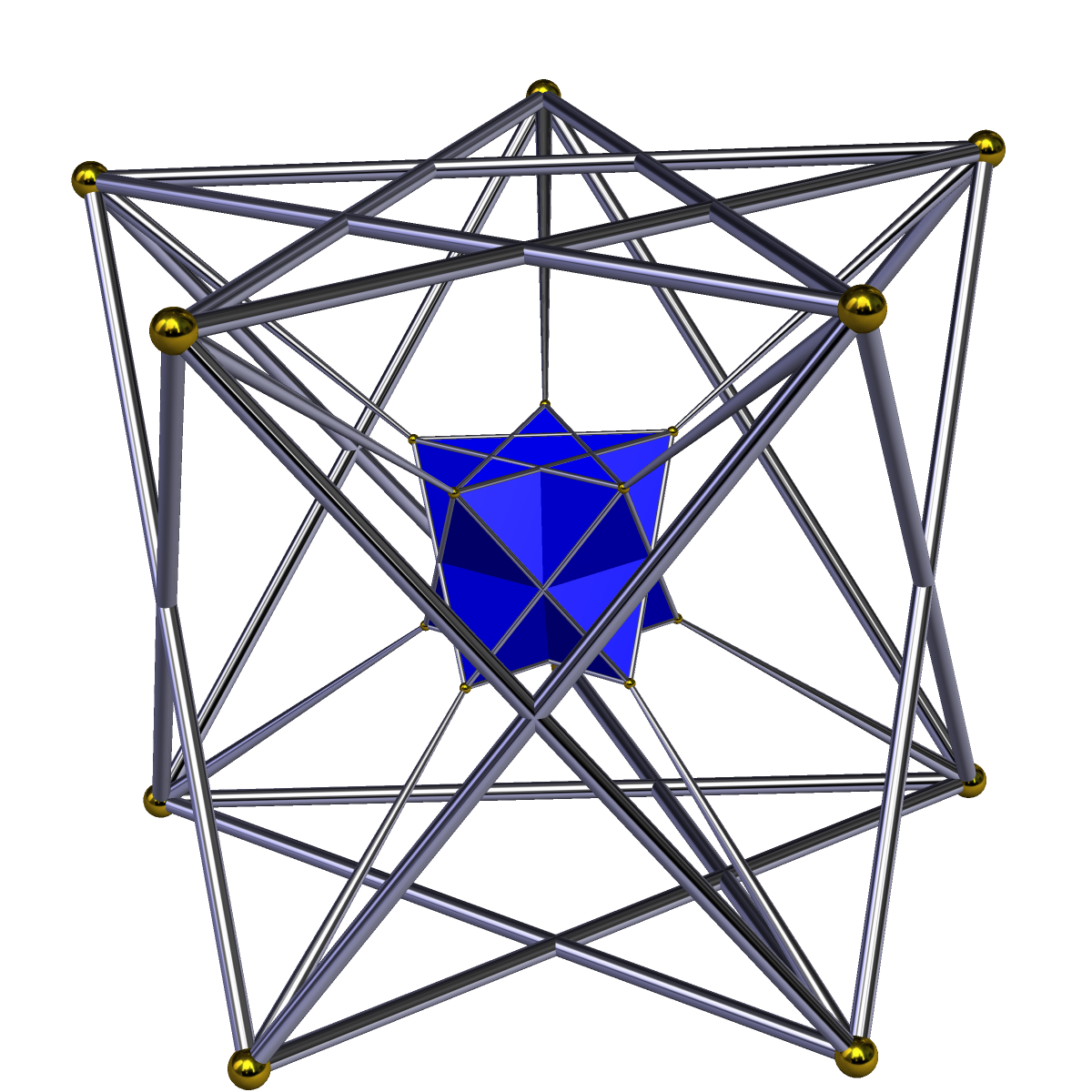
Tetrahedral Prism
In geometry, a tetrahedral prism is a convex uniform 4-polytope. This 4-polytope has 6 polyhedral cells: 2 tetrahedra connected by 4 triangular prisms. It has 14 faces: 8 triangular and 6 square. It has 16 edges and 8 vertices. It is one of 18 uniform polyhedral prisms created by using uniform prisms to connect pairs of parallel Platonic solids and Archimedean solids. Images Alternative names # Tetrahedral dyadic prism ( Norman W. Johnson) # Tepe (Jonathan Bowers: for tetrahedral prism) # Tetrahedral hyperprism # Digonal antiprismatic prism # Digonal antiprismatic hyperprism Structure The tetrahedral prism is bounded by two tetrahedra and four triangular prisms. The triangular prisms are joined to each other via their square faces, and are joined to the two tetrahedra via their triangular faces. Projections The tetrahedron-first orthographic projection of the tetrahedral prism into 3D space has a tetrahedral projection envelope. Both tetrahedral cells project onto thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedral Prism
In geometry, a tetrahedral prism is a convex uniform 4-polytope. This 4-polytope has 6 polyhedral cells: 2 tetrahedra connected by 4 triangular prisms. It has 14 faces: 8 triangular and 6 square. It has 16 edges and 8 vertices. It is one of 18 uniform polyhedral prisms created by using uniform prisms to connect pairs of parallel Platonic solids and Archimedean solids. Images Alternative names # Tetrahedral dyadic prism ( Norman W. Johnson) # Tepe (Jonathan Bowers: for tetrahedral prism) # Tetrahedral hyperprism # Digonal antiprismatic prism # Digonal antiprismatic hyperprism Structure The tetrahedral prism is bounded by two tetrahedra and four triangular prisms. The triangular prisms are joined to each other via their square faces, and are joined to the two tetrahedra via their triangular faces. Projections The tetrahedron-first orthographic projection of the tetrahedral prism into 3D space has a tetrahedral projection envelope. Both tetrahedral cells project onto thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedral Hyperprism
In geometry, a tetrahedral prism is a convex uniform 4-polytope. This 4-polytope has 6 polyhedral cells: 2 tetrahedra connected by 4 triangular prisms. It has 14 faces: 8 triangular and 6 square. It has 16 edges and 8 vertices. It is one of 18 uniform polyhedral prisms created by using uniform prisms to connect pairs of parallel Platonic solids and Archimedean solids. Images Alternative names # Tetrahedral dyadic prism (Norman W. Johnson) # Tepe (Jonathan Bowers: for tetrahedral prism) # Tetrahedral hyperprism # Digonal antiprismatic prism # Digonal antiprismatic hyperprism Structure The tetrahedral prism is bounded by two tetrahedra and four triangular prisms. The triangular prisms are joined to each other via their square faces, and are joined to the two tetrahedra via their triangular faces. Projections The tetrahedron-first orthographic projection of the tetrahedral prism into 3D space has a tetrahedral projection envelope. Both tetrahedral cells project onto this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedron
In geometry, a polyhedron (plural polyhedra or polyhedrons; ) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices. A convex polyhedron is the convex hull of finitely many points, not all on the same plane. Cubes and pyramids are examples of convex polyhedra. A polyhedron is a 3-dimensional example of a polytope, a more general concept in any number of dimensions. Definition Convex polyhedra are well-defined, with several equivalent standard definitions. However, the formal mathematical definition of polyhedra that are not required to be convex has been problematic. Many definitions of "polyhedron" have been given within particular contexts,. some more rigorous than others, and there is not universal agreement over which of these to choose. Some of these definitions exclude shapes that have often been counted as polyhedra (such as the self-crossing polyhedra) or include shapes that are often not considered as valid polyhedr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Polytope
In geometry, a uniform polytope of dimension three or higher is a vertex-transitive polytope bounded by uniform facets. The uniform polytopes in two dimensions are the regular polygons (the definition is different in 2 dimensions to exclude vertex-transitive even-sided polygons that alternate two different lengths of edges). This is a generalization of the older category of ''semiregular'' polytopes, but also includes the regular polytopes. Further, star regular faces and vertex figures ( star polygons) are allowed, which greatly expand the possible solutions. A strict definition requires uniform polytopes to be finite, while a more expansive definition allows uniform honeycombs (2-dimensional tilings and higher dimensional honeycombs) of Euclidean and hyperbolic space to be considered polytopes as well. Operations Nearly every uniform polytope can be generated by a Wythoff construction, and represented by a Coxeter diagram. Notable exceptions include the great dirhombic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3 31 Honeycomb
In 7-dimensional geometry, the 331 honeycomb is a uniform honeycomb, also given by Schläfli symbol and is composed of 321 and 7-simplex facets, with 56 and 576 of them respectively around each vertex. Construction It is created by a Wythoff construction upon a set of 8 hyperplane mirrors in 7-dimensional space. The facet information can be extracted from its Coxeter-Dynkin diagram. : Removing the node on the short branch leaves the 6-simplex facet: : Removing the node on the end of the 3-length branch leaves the 321 facet: : The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes 231 polytope. : The edge figure is determined by removing the ringed node and ringing the neighboring node. This makes 6-demicube (131). : The face figure is determined by removing the ringed node and ringing the neighboring node. This makes rectified 5-simplex (031). : The cell figure is determined by removing the ringed node of the face ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectified 5-simplex
In five-dimensional geometry, a rectified 5-simplex is a convex uniform 5-polytope, being a rectification of the regular 5-simplex. There are three unique degrees of rectifications, including the zeroth, the 5-simplex itself. Vertices of the ''rectified 5-simplex'' are located at the edge-centers of the ''5-simplex''. Vertices of the ''birectified 5-simplex'' are located in the triangular face centers of the ''5-simplex''. Rectified 5-simplex In five-dimensional geometry, a rectified 5-simplex is a uniform 5-polytope with 15 vertices, 60 edges, 80 triangular faces, 45 cells (30 tetrahedral, and 15 octahedral), and 12 4-faces (6 5-cell and 6 rectified 5-cells). It is also called 03,1 for its branching Coxeter-Dynkin diagram, shown as . E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as S. Alternate names * Rectified hexateron (Acronym: rix) (Jonathan Bowers) Coordinates The vertices of the rectified 5-simplex can be more simply positioned on a hyp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coxeter
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century. Biography Coxeter was born in Kensington to Harold Samuel Coxeter and Lucy (). His father had taken over the family business of Coxeter & Son, manufacturers of surgical instruments and compressed gases (including a mechanism for anaesthetising surgical patients with nitrous oxide), but was able to retire early and focus on sculpting and baritone singing; Lucy Coxeter was a portrait and landscape painter who had attended the Royal Academy of Arts. A maternal cousin was the architect Sir Giles Gilbert Scott. In his youth, Coxeter composed music and was an accomplished pianist at the age of 10. Roberts, Siobhan, ''King of Infinite Space: Donald Coxeter, The Man Who Saved Geometry'', Walker & Company, 2006, He felt that mathematics and music were intimately related, outlining his ide ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Antiprismatic Prism
In 4-dimensional geometry, a uniform antiprismatic prism or antiduoprism is a uniform 4-polytope with two uniform antiprism cells in two parallel 3-space hyperplanes, connected by uniform prisms cells between pairs of faces. The symmetry of a ''p''-gonal antiprismatic prism is ''p'',2+,2 order 8''p''. A p-gonal antiprismatic prism or p-gonal antiduoprism has 2 ''p''-gonal antiprism, 2 ''p''-gonal prism, and ''2p'' triangular prism cells. It has 4''p'' equilateral triangle, 4''p'' square and 4 regular ''p''-gon faces. It has 10''p'' edges, and 4''p'' vertices. Convex uniform antiprismatic prisms There is an infinite series of convex uniform antiprismatic prisms, starting with the ''digonal antiprismatic prism'' is a tetrahedral prism, with two of the tetrahedral cells degenerated into squares. The ''triangular antiprismatic prism'' is the first nondegenerate form, which is also an octahedral prism. The remainder are unique uniform 4-polytopes. Star antiprismatic prisms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Norman Johnson (mathematician)
Norman Woodason Johnson () was a mathematician at Wheaton College, Norton, Massachusetts. Early life and education Norman Johnson was born on in Chicago. His father had a bookstore and published a local newspaper. Johnson earned his undergraduate mathematics degree in 1953 at Carleton College in Northfield, Minnesota followed by a master's degree from the University of Pittsburgh. After graduating in 1953, Johnson did alternative civilian service as a conscientious objector. He earned his PhD from the University of Toronto in 1966 with a dissertation title of ''The Theory of Uniform Polytopes and Honeycombs'' under the supervision of H. S. M. Coxeter. From there, he accepted a position in the Mathematics Department of Wheaton College in Massachusetts and taught until his retirement in 1998. Career In 1966, he enumerated 92 convex non-uniform polyhedra with regular faces. Victor Zalgaller later proved (1969) that Johnson's list was complete, and the set is now known a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedral Prism YZ ZW
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has fewer than 5 faces. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets. For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another sphere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedral Hyperprism Schlegel
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has fewer than 5 faces. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets. For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another sphere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthographic Projection (geometry)
Orthographic projection (also orthogonal projection and analemma) is a means of representing three-dimensional objects in two dimensions. Orthographic projection is a form of parallel projection in which all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface. The obverse of an orthographic projection is an oblique projection, which is a parallel projection in which the projection lines are ''not'' orthogonal to the projection plane. The term ''orthographic'' sometimes means a technique in multiview projection in which principal axes or the planes of the subject are also parallel with the projection plane to create the ''primary views''. If the principal planes or axes of an object in an orthographic projection are ''not'' parallel with the projection plane, the depiction is called ''axonometric'' or an ''auxiliary views''. (''Axonometric projection'' is synonymous with ''par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |




.jpg)
