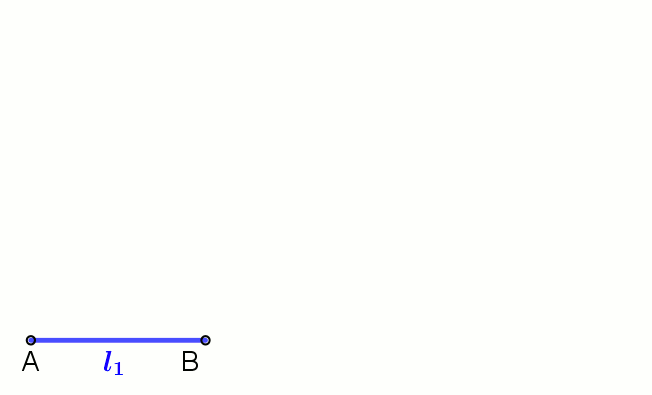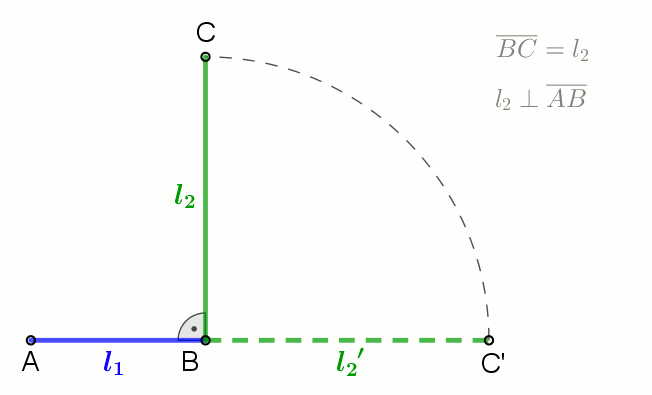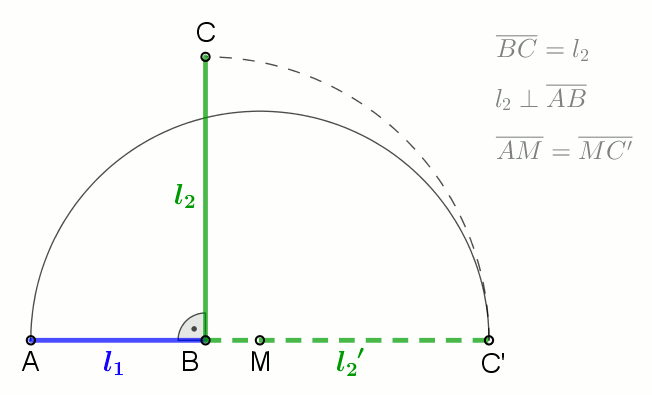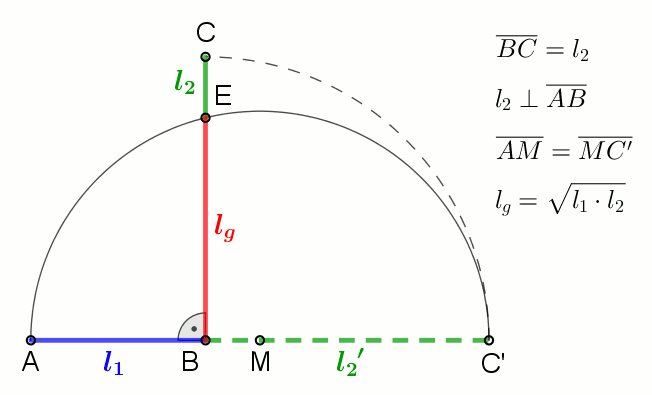|
Mean Streets Of Gadgetzan''
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value ( magnitude and sign) of a given data set. For a data set, the ''arithmetic mean'', also known as "arithmetic average", is a measure of central tendency of a finite set of numbers: specifically, the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is the '' sample mean'' (\bar) to distinguish it from the mean, or expected value, of the underlying distribution, the '' population mean'' (denoted \mu or \mu_x).Underhill, L.G.; Bradfield d. (1998) ''Introstat'', Juta and Company Ltd.p. 181/ref> Outside probability and statistics, a wide range of other notions of m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Mean
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a set of numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean is defined as the th root of the product of numbers, i.e., for a set of numbers , the geometric mean is defined as :\left(\prod_^n a_i\right)^\frac = \sqrt /math> or, equivalently, as the arithmetic mean in logscale: :\exp For instance, the geometric mean of two numbers, say 2 and 8, is just the square root of their product, that is, \sqrt = 4. As another example, the geometric mean of the three numbers 4, 1, and 1/32 is the cube root of their product (1/8), which is 1/2, that is, \sqrt = 1/2. The geometric mean applies only to positive numbers. The geometric mean is often used for a set of numbers whose values are meant to be multiplied together or are exponential in nature, such as a set of growth figures: values of the human population or inter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that the coin is fair). Examples of random phenomena include the weather conditions at some future date, the height of a randomly selected person, the fraction of male students in a school, the results of a survey to be conducted, etc. Introduction A probability distribution is a mathematical description of the probabilities of events, subsets of the sample space. The sample space, often denoted by \Omega, is the set of all possible outcomes of a random phe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson Distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and Statistical independence, independently of the time since the last event. It is named after France, French mathematician Siméon Denis Poisson (; ). The Poisson distribution can also be used for the number of events in other specified interval types such as distance, area, or volume. For instance, a call center receives an average of 180 calls per hour, 24 hours a day. The calls are independent; receiving one does not change the probability of when the next one will arrive. The number of calls received during any minute has a Poisson probability distribution with mean 3: the most likely numbers are 2 and 3 but 1 and 4 are also likely and there is a small probability of it being as low as zero and a very smal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Distribution
In probability theory and statistics, the exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts. The exponential distribution is not the same as the class of exponential families of distributions. This is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes many other distributions, like the normal, binomial, gamma, and Poisson distributions. Definitions Probability density function The probability density function (pdf) of an exponential distribution is : f(x;\lambda) = \begin \lambda ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined. For a unimodal distribution, negative skew commonly indicates that the ''tail'' is on the left side of the distribution, and positive skew indicates that the tail is on the right. In cases where one tail is long but the other tail is fat, skewness does not obey a simple rule. For example, a zero value means that the tails on both sides of the mean balance out overall; this is the case for a symmetric distribution, but can also be true for an asymmetric distribution where one tail is long and thin, and the other is short but fat. Introduction Consider the two distributions in the figure just below. Within each graph, the values on the right side of the distribution taper differently from the values on the left side. These tapering sides are called ''tail ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mid-range
In statistics, the mid-range or mid-extreme is a measure of central tendency of a sample defined as the arithmetic mean of the maximum and minimum values of the data set: :M=\frac. The mid-range is closely related to the range, a measure of statistical dispersion defined as the difference between maximum and minimum values. The two measures are complementary in sense that if one knows the mid-range and the range, one can find the sample maximum and minimum values. The mid-range is rarely used in practical statistical analysis, as it lacks efficiency as an estimator for most distributions of interest, because it ignores all intermediate points, and lacks robustness, as outliers change it significantly. Indeed, for many distributions it is one of the least efficient and least robust statistics. However, it finds some use in special cases: it is the maximally efficient estimator for the center of a uniform distribution, trimmed mid-ranges address robustness, and as an L-estima ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mode (statistics)
The mode is the value that appears most often in a set of data values. If is a discrete random variable, the mode is the value (i.e, ) at which the probability mass function takes its maximum value. In other words, it is the value that is most likely to be sampled. Like the statistical mean and median, the mode is a way of expressing, in a (usually) single number, important information about a random variable or a population. The numerical value of the mode is the same as that of the mean and median in a normal distribution, and it may be very different in highly skewed distributions. The mode is not necessarily unique to a given discrete distribution, since the probability mass function may take the same maximum value at several points , , etc. The most extreme case occurs in uniform distributions, where all values occur equally frequently. When the probability density function of a continuous distribution has multiple local maxima it is common to refer to all of the local ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Median
In statistics and probability theory, the median is the value separating the higher half from the lower half of a data sample, a population, or a probability distribution. For a data set, it may be thought of as "the middle" value. The basic feature of the median in describing data compared to the mean (often simply described as the "average") is that it is not skewed by a small proportion of extremely large or small values, and therefore provides a better representation of a "typical" value. Median income, for example, may be a better way to suggest what a "typical" income is, because income distribution can be very skewed. The median is of central importance in robust statistics, as it is the most resistant statistic, having a breakdown point of 50%: so long as no more than half the data are contaminated, the median is not an arbitrarily large or small result. Finite data set of numbers The median of a finite list of numbers is the "middle" number, when those numbers are list ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Descriptive Statistics
A descriptive statistic (in the count noun sense) is a summary statistic that quantitatively describes or summarizes features from a collection of information, while descriptive statistics (in the mass noun sense) is the process of using and analysing those statistics. Descriptive statistic is distinguished from inferential statistics (or inductive statistics) by its aim to summarize a sample, rather than use the data to learn about the population that the sample of data is thought to represent. This generally means that descriptive statistics, unlike inferential statistics, is not developed on the basis of probability theory, and are frequently nonparametric statistics. Even when a data analysis draws its main conclusions using inferential statistics, descriptive statistics are generally also presented. For example, in papers reporting on human subjects, typically a table is included giving the overall sample size, sample sizes in important subgroups (e.g., for each treatment or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Visualisation Mode Median Mean
Visualization or visualisation may refer to: *Visualization (graphics), the physical or imagining creation of images, diagrams, or animations to communicate a message * Data visualization, the graphic representation of data * Information visualization, the study of visual representations of abstract data * Music visualization, animated imagery based on a piece of music *Mental image, the experience of images without the relevant external stimuli * "Visualization", a song by Blank Banshee on the 2012 album ''Blank Banshee 0'' See also * Creative visualization (other) * Visualizer (other) * * * * Graphics * List of graphical methods, various forms of visualization * Guided imagery, a mind-body intervention by a trained practitioner * Illustration, a decoration, interpretation or visual explanation of a text, concept or process * Image, an artifact that depicts visual perception, such as a photograph or other picture * Infographics Infographics (a clipped co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Comparison Mean Median Mode
Comparison or comparing is the act of evaluating two or more things by determining the relevant, comparable characteristics of each thing, and then determining which characteristics of each are Similarity (psychology), similar to the other, which are Difference (philosophy), different, and to what degree. Where characteristics are different, the differences may then be evaluated to determine which thing is best suited for a particular purpose. The description of similarities and differences found between the two things is also called a comparison. Comparison can take many distinct forms, varying by field: To compare things, they must have characteristics that are similar enough in relevant ways to merit comparison. If two things are too different to compare in a useful way, an attempt to compare them is colloquially referred to in English as "comparing apples and oranges." Comparison is widely used in society, in science and in the arts. General usage Comparison is a natural ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |