Skewness on:
[Wikipedia]
[Google]
[Amazon]
 In
In
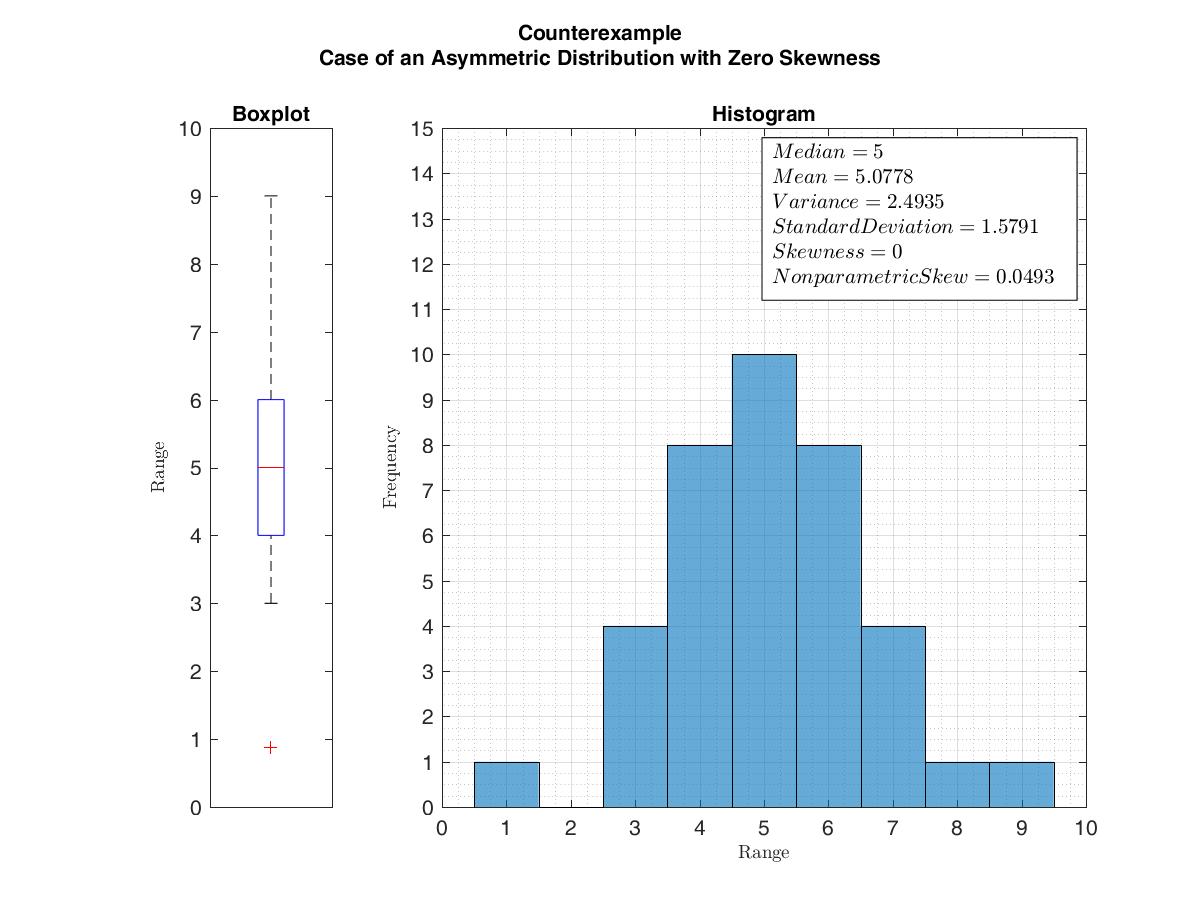
 In the older notion of nonparametric skew, defined as where is the
In the older notion of nonparametric skew, defined as where is the  For example, in the distribution of adult residents across US households, the skew is to the right. However, since the majority of cases is less than or equal to the mode, which is also the median, the mean sits in the heavier left tail. As a result, the rule of thumb that the mean is right of the median under right skew failed.
For example, in the distribution of adult residents across US households, the skew is to the right. However, since the majority of cases is less than or equal to the mode, which is also the median, the mean sits in the heavier left tail. As a result, the rule of thumb that the mean is right of the median under right skew failed.
FXSolver.com or simply the moment coefficient of skewness,
2008–2016 by Stan Brown, Oak Road Systems but should not be confused with Pearson's other skewness statistics (see below). The last equality expresses skewness in terms of the ratio of the third cumulant ''κ''3 to the 1.5th power of the second cumulant ''κ''2. This is analogous to the definition of kurtosis as the fourth cumulant normalized by the square of the second cumulant. The skewness is also sometimes denoted Skew 'X'' If ''σ'' is finite, ''μ'' is finite too and skewness can be expressed in terms of the non-central moment E 'X''3by expanding the previous formula, :
"Measuring skewness: a forgotten statistic."
Journal of Statistics Education 19.2 (2011): 1-18. (Page 7) : where is the unique symmetric unbiased estimator of the third cumulant and is the symmetric unbiased estimator of the second cumulant (i.e. the
Skewness Measures for the Weibull Distribution
{{refend
by Michel Petitjean
On More Robust Estimation of Skewness and Kurtosis
Comparison of skew estimators by Kim and White.
{{- {{Statistics, descriptive {{Theory_of_probability_distributions Moment (mathematics) Statistical deviation and dispersion
 In
In probability theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set o ...
and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined.
For a unimodal distribution, negative skew commonly indicates that the ''tail'' is on the left side of the distribution, and positive skew indicates that the tail is on the right. In cases where one tail is long but the other tail is fat, skewness does not obey a simple rule. For example, a zero value means that the tails on both sides of the mean balance out overall; this is the case for a symmetric distribution, but can also be true for an asymmetric distribution where one tail is long and thin, and the other is short but fat.
Introduction
Consider the two distributions in the figure just below. Within each graph, the values on the right side of the distribution taper differently from the values on the left side. These tapering sides are called ''tails'', and they provide a visual means to determine which of the two kinds of skewness a distribution has: # ': The left tail is longer; the mass of the distribution is concentrated on the right of the figure. The distribution is said to be ''left-skewed'', ''left-tailed'', or ''skewed to the left'', despite the fact that the curve itself appears to be skewed or leaning to the right; ''left'' instead refers to the left tail being drawn out and, often, the mean being skewed to the left of a typical center of the data. A left-skewed distribution usually appears as a ''right-leaning'' curve. # ': The right tail is longer; the mass of the distribution is concentrated on the left of the figure. The distribution is said to be ''right-skewed'', ''right-tailed'', or ''skewed to the right'', despite the fact that the curve itself appears to be skewed or leaning to the left; ''right'' instead refers to the right tail being drawn out and, often, the mean being skewed to the right of a typical center of the data. A right-skewed distribution usually appears as a ''left-leaning'' curve. Skewness in a data series may sometimes be observed not only graphically but by simple inspection of the values. For instance, consider the numeric sequence (49, 50, 51), whose values are evenly distributed around a central value of 50. We can transform this sequence into a negatively skewed distribution by adding a value far below the mean, which is probably a negative outlier, e.g. (40, 49, 50, 51). Therefore, the mean of the sequence becomes 47.5, and the median is 49.5. Based on the formula of nonparametric skew, defined as the skew is negative. Similarly, we can make the sequence positively skewed by adding a value far above the mean, which is probably a positive outlier, e.g. (49, 50, 51, 60), where the mean is 52.5, and the median is 50.5. As mentioned earlier, a unimodal distribution with zero value of skewness does not imply that this distribution is symmetric necessarily. However, a symmetric unimodal or multimodal distribution always has zero skewness.
Relationship of mean and median
The skewness is not directly related to the relationship between the mean and median: a distribution with negative skew can have its mean greater than or less than the median, and likewise for positive skew. In the older notion of nonparametric skew, defined as where is the
In the older notion of nonparametric skew, defined as where is the mean
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value ( magnitude and sign) of a given data set.
For a data set, the '' ari ...
, is the median, and is the standard deviation, the skewness is defined in terms of this relationship: positive/right nonparametric skew means the mean is greater than (to the right of) the median, while negative/left nonparametric skew means the mean is less than (to the left of) the median. However, the modern definition of skewness and the traditional nonparametric definition do not always have the same sign: while they agree for some families of distributions, they differ in some of the cases, and conflating them is misleading.
If the distribution is symmetric, then the mean is equal to the median, and the distribution has zero skewness. If the distribution is both symmetric and unimodal, then the mean
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value ( magnitude and sign) of a given data set.
For a data set, the '' ari ...
= median = mode. This is the case of a coin toss or the series 1,2,3,4,... Note, however, that the converse is not true in general, i.e. zero skewness (defined below) does not imply that the mean is equal to the median.
A 2005 journal article points out:Many textbooks teach a rule of thumb stating that the mean is right of the median under right skew, and left of the median under left skew. This rule fails with surprising frequency. It can fail in multimodal distributions, or in distributions where one tail is long but the other is heavy. Most commonly, though, the rule fails in discrete distributions where the areas to the left and right of the median are not equal. Such distributions not only contradict the textbook relationship between mean, median, and skew, they also contradict the textbook interpretation of the median.
 For example, in the distribution of adult residents across US households, the skew is to the right. However, since the majority of cases is less than or equal to the mode, which is also the median, the mean sits in the heavier left tail. As a result, the rule of thumb that the mean is right of the median under right skew failed.
For example, in the distribution of adult residents across US households, the skew is to the right. However, since the majority of cases is less than or equal to the mode, which is also the median, the mean sits in the heavier left tail. As a result, the rule of thumb that the mean is right of the median under right skew failed.
Definition
Fisher's moment coefficient of skewness
The skewness of a random variable ''X'' is the third standardized moment , defined as: : where ''μ'' is the mean, ''σ'' is the standard deviation, E is the expectation operator, ''μ''3 is the thirdcentral moment
In probability theory and statistics, a central moment is a moment of a probability distribution of a random variable about the random variable's mean; that is, it is the expected value of a specified integer power of the deviation of the random ...
, and ''κ''''t'' are the ''t''-th cumulants. It is sometimes referred to as Pearson's moment coefficient of skewness,Pearson's moment coefficient of skewnessFXSolver.com or simply the moment coefficient of skewness,
2008–2016 by Stan Brown, Oak Road Systems but should not be confused with Pearson's other skewness statistics (see below). The last equality expresses skewness in terms of the ratio of the third cumulant ''κ''3 to the 1.5th power of the second cumulant ''κ''2. This is analogous to the definition of kurtosis as the fourth cumulant normalized by the square of the second cumulant. The skewness is also sometimes denoted Skew 'X'' If ''σ'' is finite, ''μ'' is finite too and skewness can be expressed in terms of the non-central moment E 'X''3by expanding the previous formula, :
Examples
Skewness can be infinite, as when : where the third cumulants are infinite, or as when : where the third cumulant is undefined. Examples of distributions with finite skewness include the following. * Anormal distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
:
f(x) = \frac e^
The parameter \mu i ...
and any other symmetric distribution with finite third moment has a skewness of 0
* A half-normal distribution has a skewness just below 1
* An exponential distribution has a skewness of 2
* A lognormal distribution can have a skewness of any positive value, depending on its parameters
Sample skewness
For a sample of ''n'' values, two natural estimators of the population skewness are : and : where is the sample mean, ''s'' is the sample standard deviation, ''m''2 is the (biased) sample second centralmoment
Moment or Moments may refer to:
* Present time
Music
* The Moments, American R&B vocal group Albums
* ''Moment'' (Dark Tranquillity album), 2020
* ''Moment'' (Speed album), 1998
* ''Moments'' (Darude album)
* ''Moments'' (Christine Guldbrand ...
, and ''m''3 is the sample third central moment. is a method of moments estimator.
Another common definition of the ''sample skewness'' isDoane, David P., and Lori E. Seward"Measuring skewness: a forgotten statistic."
Journal of Statistics Education 19.2 (2011): 1-18. (Page 7) : where is the unique symmetric unbiased estimator of the third cumulant and is the symmetric unbiased estimator of the second cumulant (i.e. the
sample variance
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its population mean or sample mean. Variance is a measure of dispersion, meaning it is a measure of how far a set of number ...
). This adjusted Fisher–Pearson standardized moment coefficient is the version found in Excel
ExCeL London (an abbreviation for Exhibition Centre London) is an exhibition centre, international convention centre and former hospital in the Custom House area of Newham, East London. It is situated on a site on the northern quay of the ...
and several statistical packages including Minitab, SAS
SAS or Sas may refer to:
Arts, entertainment, and media
* ''SAS'' (novel series), a French book series by Gérard de Villiers
* ''Shimmer and Shine'', an American animated children's television series
* Southern All Stars, a Japanese rock ba ...
and SPSS.
Under the assumption that the underlying random variable is normally distributed, it can be shown that all three ratios , and are unbiased and consistent estimators of the population skewness , with , i.e., their distributions converge to a normal distribution with mean 0 and variance 6 ( Fisher, 1930). The variance of the sample skewness is thus approximately for sufficiently large samples. More precisely, in a random sample of size ''n'' from a normal distribution,Duncan Cramer (1997) Fundamental Statistics for Social Research. Routledge. (p 85)
:
In normal samples, has the smaller variance of the three estimators, with
:
For non-normal distributions, , and are generally biased estimators of the population skewness ; their expected values can even have the opposite sign from the true skewness. For instance, a mixed distribution consisting of very thin Gaussians centred at −99, 0.5, and 2 with weights 0.01, 0.66, and 0.33 has a skewness of about −9.77, but in a sample of 3 has an expected value of about 0.32, since usually all three samples are in the positive-valued part of the distribution, which is skewed the other way.
Applications
Skewness is a descriptive statistic that can be used in conjunction with the histogram and the normalquantile plot
In statistics and probability, quantiles are cut points dividing the range of a probability distribution into continuous intervals with equal probabilities, or dividing the observations in a sample in the same way. There is one fewer quantile t ...
to characterize the data or distribution.
Skewness indicates the direction and relative magnitude of a distribution's deviation from the normal distribution.
With pronounced skewness, standard statistical inference procedures such as a confidence interval for a mean will be not only incorrect, in the sense that the true coverage level will differ from the nominal (e.g., 95%) level, but they will also result in unequal error probabilities on each side.
Skewness can be used to obtain approximate probabilities and quantiles of distributions (such as value at risk in finance) via the Cornish-Fisher expansion.
Many models assume normal distribution; i.e., data are symmetric about the mean. The normal distribution has a skewness of zero. But in reality, data points may not be perfectly symmetric. So, an understanding of the skewness of the dataset indicates whether deviations from the mean are going to be positive or negative.
D'Agostino's K-squared test is a goodness-of-fit normality test based on sample skewness and sample kurtosis.
Other measures of skewness
Other measures of skewness have been used, including simpler calculations suggested by Karl Pearson (not to be confused with Pearson's moment coefficient of skewness, see above). These other measures are:Pearson's first skewness coefficient (mode skewness)
The Pearson mode skewness, or first skewness coefficient, is defined as : .Pearson's second skewness coefficient (median skewness)
The Pearson median skewness, or second skewness coefficient, is defined as : . Which is a simple multiple of the nonparametric skew. Worth noticing that, since skewness is not related to an order relationship between mode, mean and median, the sign of these coefficients does not give information about the type of skewness (left/right).Quantile-based measures
Bowley's measure of skewness (from 1901),Kenney JF and Keeping ES (1962) ''Mathematics of Statistics, Pt. 1, 3rd ed.'', Van Nostrand, (page 102). also called Yule's coefficient (from 1912) is defined as: : where ''Q'' is the quantile function (i.e., the inverse of thecumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ev ...
). The numerator is difference between the average of the upper and lower quartiles (a measure of location) and the median (another measure of location), while the denominator is the semi-interquartile range
In descriptive statistics, the interquartile range (IQR) is a measure of statistical dispersion, which is the spread of the data. The IQR may also be called the midspread, middle 50%, fourth spread, or H‑spread. It is defined as the difference ...
, which for symmetric distributions is the MAD measure of dispersion.
Other names for this measure are Galton's measure of skewness,{{harvp, Johnson, NL, Kotz, S, Balakrishnan, N, 1994 p. 3 and p. 40 the Yule–Kendall indexWilks DS (1995) ''Statistical Methods in the Atmospheric Sciences'', p 27. Academic Press. {{isbn, 0-12-751965-3 and the quartile skewness,
Similarly, Kelly's measure of skewness is defined as
:
A more general formulation of a skewness function was described by Groeneveld, R. A. and Meeden, G. (1984):{{Cite journal , doi = 10.2307/2987742 , last1 = Groeneveld , first1 = R.A. , last2 = Meeden , first2 = G. , year = 1984 , title = Measuring Skewness and Kurtosis , jstor = 2987742, journal = The Statistician , volume = 33 , issue = 4, pages = 391–399
MacGillivray (1992)Hinkley DV (1975) "On power transformations to symmetry", '' Biometrika, 62, 101–111
:
The function ''γ''(''u'') satisfies −1 ≤ ''γ''(''u'') ≤ 1 and is well defined without requiring the existence of any moments of the distribution. Bowley's measure of skewness is γ(''u'') evaluated at ''u'' = 3/4 while Kelly's measure of skewness is γ(''u'') evaluated at ''u'' = 9/10. This definition leads to a corresponding overall measure of skewnessMacGillivray (1992) defined as the supremum of this over the range 1/2 ≤ ''u'' < 1. Another measure can be obtained by integrating the numerator and denominator of this expression.
Quantile-based skewness measures are at first glance easy to interpret, but they often show significantly larger sample variations than moment-based methods. This means that often samples from a symmetric distribution (like the uniform distribution) have a large quantile-based skewness, just by chance.
Groeneveld and Meeden's coefficient
Groeneveld and Meeden have suggested, as an alternative measure of skewness, : where ''μ'' is the mean, ''ν'' is the median, , ..., is the absolute value, and ''E''() is the expectation operator. This is closely related in form to Pearson's second skewness coefficient.L-moments
Use of L-moments in place of moments provides a measure of skewness known as the L-skewness.{{cite journal , last=Hosking , first= J.R.M. , year=1992 , title=Moments or L moments? An example comparing two measures of distributional shape , journal=The American Statistician , volume=46 , number=3 , pages=186–189 , jstor=2685210 , doi=10.2307/2685210Distance skewness
A value of skewness equal to zero does not imply that the probability distribution is symmetric. Thus there is a need for another measure of asymmetry that has this property: such a measure was introduced in 2000. It is called distance skewness and denoted by dSkew. If ''X'' is a random variable taking values in the ''d''-dimensional Euclidean space, ''X'' has finite expectation, ''X''{{' is an independent identically distributed copy of ''X'', and denotes the norm in the Euclidean space, then a simple ''measure of asymmetry'' with respect to location parameter θ is : and dSkew(''X'') := 0 for ''X'' = θ (with probability 1). Distance skewness is always between 0 and 1, equals 0 if and only if ''X'' is diagonally symmetric with respect to θ (''X'' and 2θ−''X'' have the same probability distribution) and equals 1 if and only if X is a constant ''c'' () with probability one.Szekely, G. J. and Mori, T. F. (2001) "A characteristic measure of asymmetry and its application for testing diagonal symmetry", ''Communications in Statistics – Theory and Methods'' 30/8&9, 1633–1639. Thus there is a simple consistent statistical test of diagonal symmetry based on the sample distance skewness: :Medcouple
The medcouple is a scale-invariant robust measure of skewness, with a breakdown point of 25%.{{cite journal , author=G. Brys , author2=M. Hubert, author2-link=Mia Hubert , author3=A. Struyf , date=November 2004 , title=A Robust Measure of Skewness , journal=Journal of Computational and Graphical Statistics , volume=13 , issue=4 , pages=996–1017 , doi=10.1198/106186004X12632, s2cid=120919149 It is the median of the values of the kernel function : taken over all couples such that , where is the median of the sample . It can be seen as the median of all possible quantile skewness measures.See also
{{Portal, Mathematics * Bragg peak * Coskewness * Kurtosis * Shape parameters * Skew normal distribution * Skewness riskReferences
Citations
{{ReflistSources
{{refbegin * {{cite book, author1=Johnson, NL, author2=Kotz, S, author3=Balakrishnan, N, year=1994, title=Continuous Univariate Distributions, volume=1, edition=2, publisher=Wiley, isbn=0-471-58495-9 * {{cite journal , last1 = MacGillivray , first1 = HL , year = 1992 , title = Shape properties of the g- and h- and Johnson families , journal = Communications in Statistics - Theory and Methods , volume = 21 , issue = 5, pages = 1244–1250 , doi = 10.1080/03610929208830842 * Premaratne, G., Bera, A. K. (2001). Adjusting the Tests for Skewness and Kurtosis for Distributional Misspecifications. Working Paper Number 01-0116, University of Illinois. Forthcoming in Comm in Statistics, Simulation and Computation. 2016 1-15 * Premaratne, G., Bera, A. K. (2000). Modeling Asymmetry and Excess Kurtosis in Stock Return Data. Office of Research Working Paper Number 00-0123, University of Illinois.Skewness Measures for the Weibull Distribution
{{refend
External links
{{Wikiversity {{Commons category, Skewness (statistics) *{{springer, title=Asymmetry coefficient, id=p/a013590by Michel Petitjean
On More Robust Estimation of Skewness and Kurtosis
Comparison of skew estimators by Kim and White.
{{- {{Statistics, descriptive {{Theory_of_probability_distributions Moment (mathematics) Statistical deviation and dispersion