|
Zeta Constant
In mathematics, the Riemann zeta function is a function in complex analysis, which is also important in number theory. It is often denoted and is named after the mathematician Bernhard Riemann. When the argument is a real number greater than one, the zeta function satisfies the equation \zeta(s) = \sum_^\infty\frac \, . It can therefore provide the sum of various convergent Series (mathematics), infinite series, such as \zeta(2) = \frac + \frac + \frac + \ldots \, . Explicit or numerically efficient formulae exist for at integer arguments, all of which have real values, including this example. This article lists these formulae, together with tables of values. It also includes derivatives and some series composed of the zeta function at integer arguments. The same equation in above also holds when is a complex number whose real part is greater than one, ensuring that the infinite sum still converges. The zeta function can then be extended to the whole of the complex plane by an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pole (complex Analysis)
In complex analysis (a branch of mathematics), a pole is a certain type of singularity of a complex-valued function of a complex variable. In some sense, it is the simplest type of singularity. Technically, a point is a pole of a function if it is a zero of the function and is holomorphic in some neighbourhood of (that is, complex differentiable in a neighbourhood of ). A function is meromorphic in an open set if for every point of there is a neighborhood of in which either or is holomorphic. If is meromorphic in , then a zero of is a pole of , and a pole of is a zero of . This induces a duality between ''zeros'' and ''poles'', that is fundamental for the study of meromorphic functions. For example, if a function is meromorphic on the whole complex plane plus the point at infinity, then the sum of the multiplicities of its poles equals the sum of the multiplicities of its zeros. Definitions A function of a complex variable is holomorphic in an open domai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
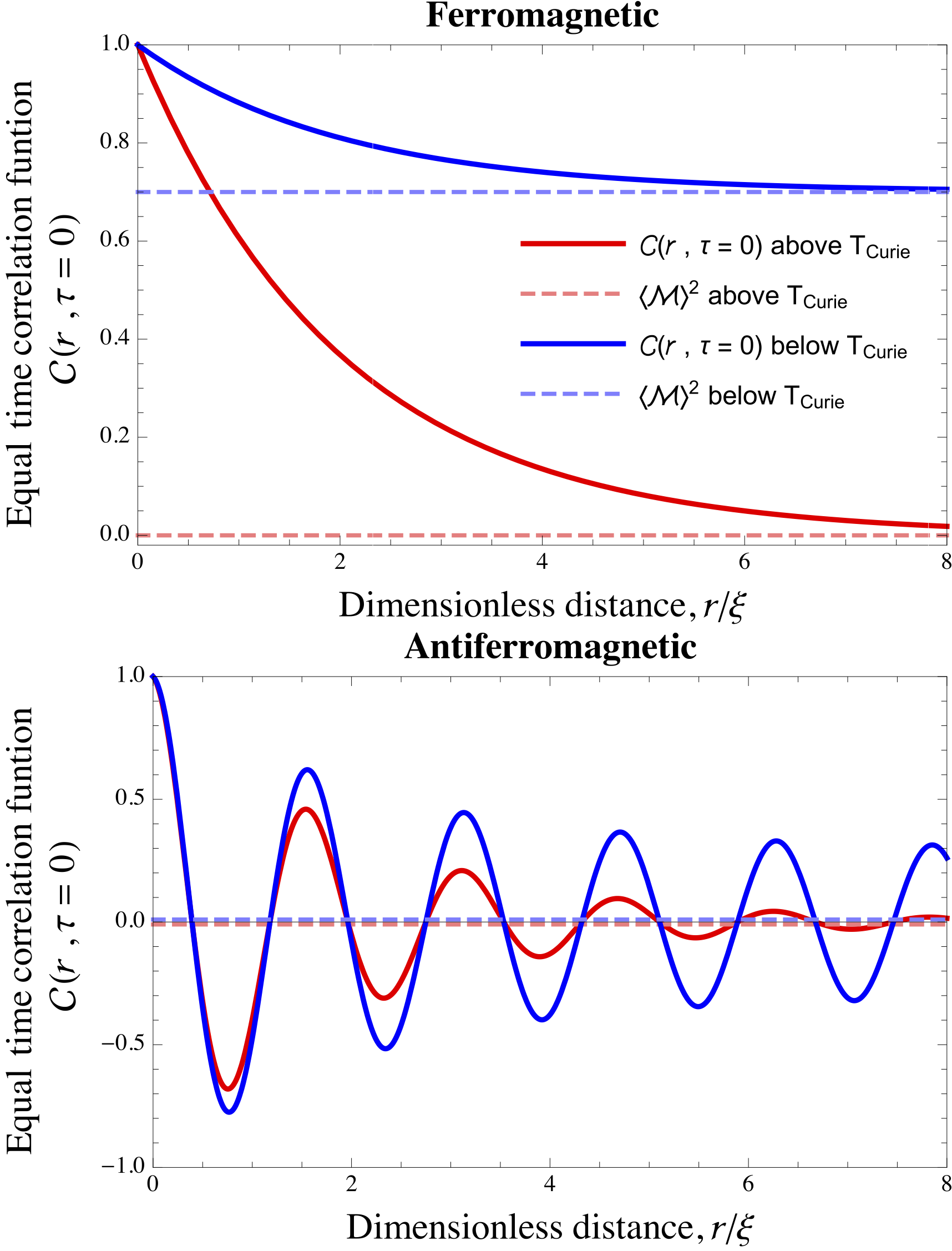
Correlation Function (statistical Mechanics)
In statistical mechanics, the correlation function is a measure of the order in a system, as characterized by a mathematical correlation function. Correlation functions describe how microscopic variables, such as spin and density, at different positions are related. More specifically, correlation functions quantify how microscopic variables co-vary with one another on average across space and time. A classic example of such spatial correlations is in ferro- and antiferromagnetic materials, where the spins prefer to align parallel and antiparallel with their nearest neighbors, respectively. The spatial correlation between spins in such materials is shown in the figure to the right. Definitions The most common definition of a correlation function is the canonical ensemble (thermal) average of the scalar product of two random variables, s_1 and s_2, at positions R and R+r and times t and t+\tau: C (r,\tau) = \langle \mathbf(R,t) \cdot \mathbf(R+r,t+\tau)\rangle\ - \langle \mathbf( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apéry's Theorem
In mathematics, Apéry's theorem is a result in number theory that states the Apéry's constant ζ(3) is irrational. That is, the number :\zeta(3) = \sum_^\infty \frac = \frac + \frac + \frac + \cdots = 1.2020569\ldots cannot be written as a fraction p/q where ''p'' and ''q'' are integers. The theorem is named after Roger Apéry. The special values of the Riemann zeta function at even integers 2n (n > 0) can be shown in terms of Bernoulli numbers to be irrational, while it remains open whether the function's values are in general rational or not at the odd integers 2n+1 (n > 1) (though they are conjectured to be irrational). History Leonhard Euler proved that if ''n'' is a positive integer then :\frac + \frac + \frac + \frac + \cdots = \frac\pi^ for some rational number p/q. Specifically, writing the infinite series on the left as \zeta(2n), he showed :\zeta(2n) = (-1)^\frac where the B_n are the rational Bernoulli numbers. Once it was proved that \pi^n is always irratio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Planck's Law
In physics, Planck's law describes the spectral density of electromagnetic radiation emitted by a black body in thermal equilibrium at a given temperature , when there is no net flow of matter or energy between the body and its environment. At the end of the 19th century, physicists were unable to explain why the observed spectrum of black-body radiation, which by then had been accurately measured, diverged significantly at higher frequencies from that predicted by existing theories. In 1900, German physicist Max Planck heuristically derived a formula for the observed spectrum by assuming that a hypothetical electrically charged oscillator in a cavity that contained black-body radiation could only change its energy in a minimal increment, , that was proportional to the frequency of its associated electromagnetic wave. This resolved the problem of the ultraviolet catastrophe predicted by classical physics. This discovery was a pioneering insight of modern physics and is of fundam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apéry's Constant
In mathematics, Apéry's constant is the sum of the reciprocals of the positive cubes. That is, it is defined as the number : \begin \zeta(3) &= \sum_^\infty \frac \\ &= \lim_ \left(\frac + \frac + \cdots + \frac\right), \end where is the Riemann zeta function. It has an approximate value of : . The constant is named after Roger Apéry. It arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio using quantum electrodynamics. It also arises in the analysis of random minimum spanning trees and in conjunction with the gamma function when solving certain integrals involving exponential functions in a quotient, which appear occasionally in physics, for instance, when evaluating the two-dimensional case of the Debye model and the Stefan–Boltzmann law. Irrational number was named ''Apéry's constant'' after the French mathematician Roger Apéry, who proved in 1978 that it is an ir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Series (mathematics)
In mathematics, the harmonic series is the infinite series formed by summing all positive unit fractions: \sum_^\infty\frac = 1 + \frac + \frac + \frac + \frac + \cdots. The first n terms of the series sum to approximately \ln n + \gamma, where \ln is the natural logarithm and \gamma\approx0.577 is the Euler–Mascheroni constant. Because the logarithm has arbitrarily large values, the harmonic series does not have a finite limit: it is a divergent series. Its divergence was proven in the 14th century by Nicole Oresme using a precursor to the Cauchy condensation test for the convergence of infinite series. It can also be proven to diverge by comparing the sum to an integral, according to the integral test for convergence. Applications of the harmonic series and its partial sums include Euler's proof that there are infinitely many prime numbers, the analysis of the coupon collector's problem on how many random trials are needed to provide a complete range of responses, the co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generating Function
In mathematics, a generating function is a way of encoding an infinite sequence of numbers () by treating them as the coefficients of a formal power series. This series is called the generating function of the sequence. Unlike an ordinary series, the ''formal'' power series is not required to converge: in fact, the generating function is not actually regarded as a function, and the "variable" remains an indeterminate. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general linear recurrence problem. One can generalize to formal power series in more than one indeterminate, to encode information about infinite multi-dimensional arrays of numbers. There are various types of generating functions, including ordinary generating functions, exponential generating functions, Lambert series, Bell series, and Dirichlet series; definitions and examples are given below. Every sequence in principle has a generating function of each type (except ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernoulli Number
In mathematics, the Bernoulli numbers are a sequence of rational numbers which occur frequently in analysis. The Bernoulli numbers appear in (and can be defined by) the Taylor series expansions of the tangent and hyperbolic tangent functions, in Faulhaber's formula for the sum of ''m''-th powers of the first ''n'' positive integers, in the Euler–Maclaurin formula, and in expressions for certain values of the Riemann zeta function. The values of the first 20 Bernoulli numbers are given in the adjacent table. Two conventions are used in the literature, denoted here by B^_n and B^_n; they differ only for , where B^_1=-1/2 and B^_1=+1/2. For every odd , . For every even , is negative if is divisible by 4 and positive otherwise. The Bernoulli numbers are special values of the Bernoulli polynomials B_n(x), with B^_n=B_n(0) and B^+_n=B_n(1). The Bernoulli numbers were discovered around the same time by the Swiss mathematician Jacob Bernoulli, after whom they are named, and indepe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
OEIS
The On-Line Encyclopedia of Integer Sequences (OEIS) is an online database of integer sequences. It was created and maintained by Neil Sloane while researching at AT&T Labs. He transferred the intellectual property and hosting of the OEIS to the OEIS Foundation in 2009. Sloane is chairman of the OEIS Foundation. OEIS records information on integer sequences of interest to both professional and amateur mathematicians, and is widely cited. , it contains over 350,000 sequences, making it the largest database of its kind. Each entry contains the leading terms of the sequence, keywords, mathematical motivations, literature links, and more, including the option to generate a graph or play a musical representation of the sequence. The database is searchable by keyword, by subsequence, or by any of 16 fields. History Neil Sloane started collecting integer sequences as a graduate student in 1965 to support his work in combinatorics. The database was at first stored on punched cards. H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wien Approximation
Wien's approximation (also sometimes called Wien's law or the Wien distribution law) is a law of physics used to describe the spectrum of thermal radiation (frequently called the blackbody function). This law was first derived by Wilhelm Wien in 1896. The equation does accurately describe the short wavelength (high frequency) spectrum of thermal emission from objects, but it fails to accurately fit the experimental data for long wavelengths (low frequency) emission. Details Wien derived his law from thermodynamic arguments, several years before Planck introduced the quantization of radiation. Wien's original paper did not contain the Planck constant. In this paper, Wien took the wavelength of black body radiation and combined it with the Maxwell–Boltzmann distribution for atoms. The exponential curve was created by the use of Euler's number e raised to the power of the temperature multiplied by a constant. Fundamental constants were later introduced by Max Planck ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stefan–Boltzmann Law
The Stefan–Boltzmann law describes the power radiated from a black body in terms of its temperature. Specifically, the Stefan–Boltzmann law states that the total energy radiated per unit surface area of a black body across all wavelengths per unit time j^ (also known as the black-body ''radiant emittance'') is directly proportional to the fourth power of the black body's thermodynamic temperature ''T'': : j^ = \sigma T^. The constant of proportionality ''σ'', called the Stefan–Boltzmann constant, is derived from other known physical constants. Since 2019, the value of the constant is : \sigma=\frac = 5.670374419\times 10^\, \mathrm, where ''k'' is the Boltzmann constant, ''h'' is Planck's constant, and ''c'' is the speed of light in a vacuum. The radiance from a specified angle of view (watts per square metre per steradian) is given by : L = \frac\pi = \frac\sigma\pi T^. A body that does not absorb all incident radiation (sometimes known as a grey body) emits ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |