Correlation function (statistical mechanics)

In statistical mechanics, the correlation function is a measure of the order in a system, as characterized by a mathematical correlation function. Correlation functions describe how microscopic variables, such as spin and density, at different positions or times are related. More specifically, correlation functions measure quantitatively the extent to which microscopic variables fluctuate together, on average, across space and/or time. Keep in mind that correlation doesn’t automatically equate to causation. So, even if there’s a non-zero correlation between two points in space or time, it doesn’t mean there is a direct causal link between them. Sometimes, a correlation can exist without any causal relationship. This could be purely coincidental or due to other underlying factors, known as confounding variables, which cause both points to covary (statistically).

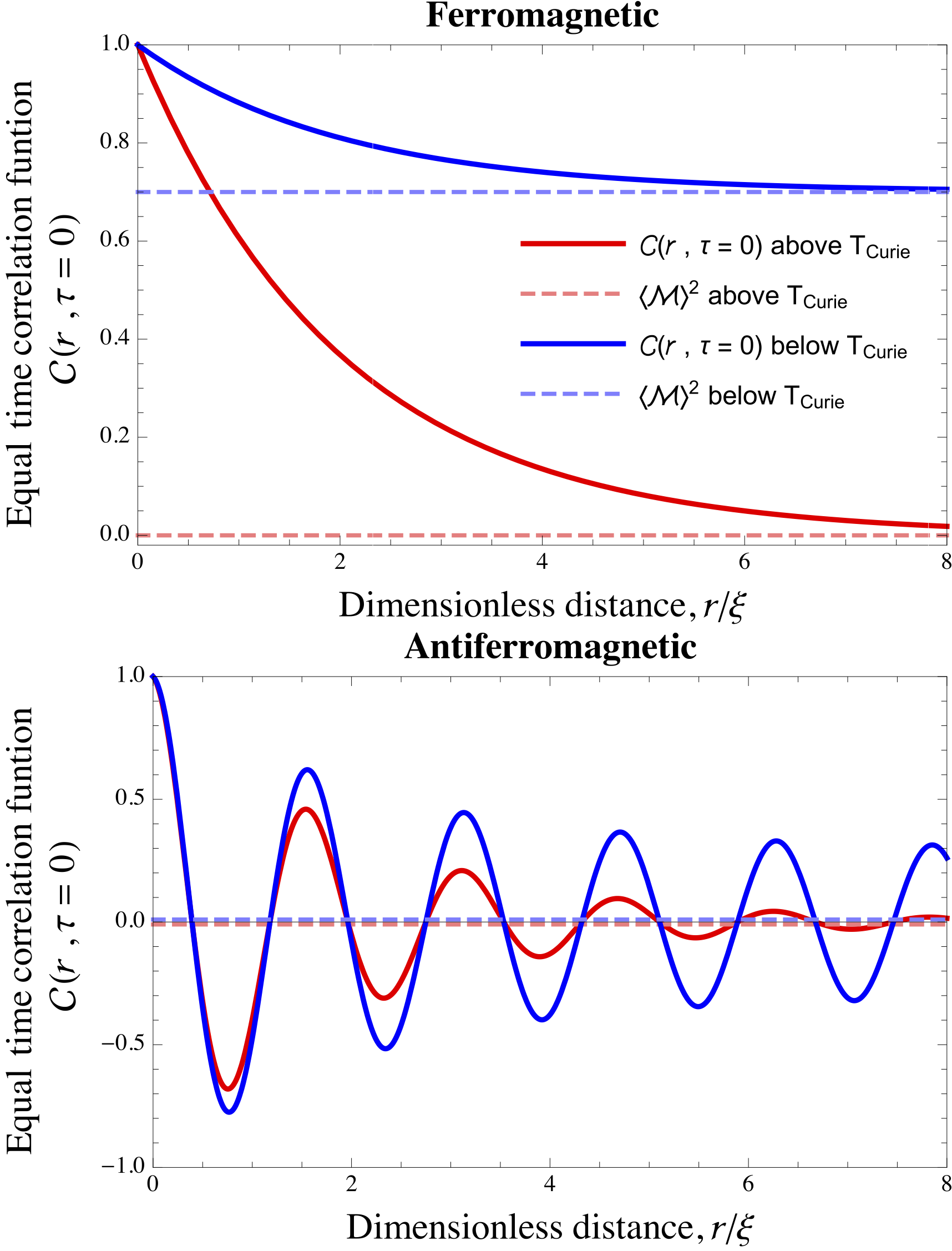
A classic example of spatial correlation can be seen in ferromagnetic and antiferromagnetic materials. In these materials, atomic spins tend to align in parallel and antiparallel configurations with their adjacent counterparts, respectively. The figure on the right visually represents this spatial correlation between spins in such materials.

Definitions

The most common definition of a correlation function is the canonical ensemble (thermal) average of the scalar product of two random variables, $s_1$ and $s_2$, at positions $R$ and $R+r$ and times $t$ and $t+\tau$:
$C (r,\tau) = \langle \mathbf(R,t) \cdot \mathbf(R+r,t+\tau)\rangle\ - \langle \mathbf(R,t) \rangle\langle \mathbf(R+r,t+\tau) \rangle\,.$

Here the brackets, $\langle \cdot \rangle$, indicate the above-mentioned thermal average. It is important to note here, however, that while the brackets are called an average, they are calculated as an expected value, not an average value. It is a matter of convention whether one subtracts the uncorrelated average product of $s_1$ and $s_2$, $\langle \mathbf(R,t) \rangle\langle \mathbf(R+r,t+\tau) \rangle$ from the correlated product, $\langle \mathbf(R,t) \cdot \mathbf(R+r,t+\tau)\rangle$, with the convention differing among fields. The most common uses of correlation functions are when $s_1$ and $s_2$ describe the same variable, such as a spin-spin correlation function, or a particle position-position correlation function in an elemental liquid or a solid (often called a Radial distribution function or a pair correlation function). Correlation functions between the same random variable are autocorrelation functions. However, in statistical mechanics, not all correlation functions are autocorrelation functions. For example, in multicomponent condensed phases, the pair correlation function between different elements is often of interest. Such mixed-element pair correlation functions are an example of cross-correlation functions, as the random variables $s_1$ and $s_2$ represent the average variations in density as a function position for two distinct elements.

Equilibrium equal-time (spatial) correlation functions

Often, one is interested in solely the ''spatial'' influence of a given random variable, say the direction of a spin, on its local environment, without considering later times, $\tau$. In this case, we neglect the time evolution of the system, so the above definition is re-written with $\tau = 0$. This defines the equal-time correlation function, $C(r,0)$. It is written as:
$C (r,0) = \langle \mathbf(R,t) \cdot \mathbf(R+r,t)\rangle\ - \langle \mathbf(R,t) \rangle\langle \mathbf(R+r,t) \rangle\,.$

Often, one omits the reference time, $t$, and reference radius, $R$, by assuming equilibrium (and thus time invariance of the ensemble) and averaging over all sample positions, yielding:
$C (r) = \langle \mathbf(0) \cdot \mathbf(r)\rangle\ - \langle \mathbf(0) \rangle\langle \mathbf(r) \rangle$
where, again, the choice of whether to subtract the uncorrelated variables differs among fields. The Radial distribution function is an example of an equal-time correlation function where the uncorrelated reference is generally not subtracted. Other equal-time spin-spin correlation functions are shown on this page for a variety of materials and conditions.

Equilibrium equal-position (temporal) correlation functions

One might also be interested in the ''temporal'' evolution of microscopic variables. In other words, how the value of a microscopic variable at a given position and time, $R$ and $t$, influences the value of the same microscopic variable at a later time, $t+\tau$ (and usually at the same position). Such temporal correlations are quantified via equal-position correlation functions, $C (0,\tau)$. They are defined analogously to above equal-time correlation functions, but we now neglect spatial dependencies by setting $r=0$, yielding:
$C (0,\tau) = \langle \mathbf(R,t) \cdot \mathbf(R,t+\tau)\rangle\ - \langle \mathbf(R,t) \rangle\langle \mathbf(R,t+\tau) \rangle\,.$

Assuming equilibrium (and thus time invariance of the ensemble) and averaging over all sites in the sample gives a simpler expression for the equal-position correlation function as for the equal-time correlation function:
$C (\tau) = \langle \mathbf(0) \cdot \mathbf(\tau)\rangle\ - \langle \mathbf(0) \rangle\langle \mathbf(\tau) \rangle\,.$

The above assumption may seem non-intuitive at first: how can an ensemble which is time-invariant have a non-uniform temporal correlation function? Temporal correlations remain relevant to talk about in equilibrium systems because a time-invariant, ''macroscopic'' ensemble can still have non-trivial temporal dynamics ''microscopically''. One example is in diffusion. A single-phase system at equilibrium has a homogeneous composition macroscopically. However, if one watches the microscopic movement of each atom, fluctuations in composition are constantly occurring due to the quasi-random walks taken by the individual atoms. Statistical mechanics allows one to make insightful statements about the temporal behavior of such fluctuations of equilibrium systems. This is discussed below in the section on the temporal evolution of correlation functions and Onsager's regression hypothesis.

Time correlation function

Time correlation function plays a significant role in nonequilibrium statistical mechanics as partition function does in equilibrium statistical mechanics. For instance, transport coefficients are closely related to time correlation functions through the Fourier transform; and the Green-Kubo relations, used to calculate relaxation and dissipation processes in a system, are expressed in terms of equilibrium time correlation functions. The time correlation function of two observable $A$ and $B$ is defined as,
$C_ (t_1, t_2) = \langle A(t_1) B(t_2) \rangle$
and this definition applies for both classical and quantum version. For stationary (equilibrium) system, the time origin is irrelevant, and $C_(\tau)=C_ (t_1, t_2)$, with $\tau = t_2 - t_1$ as the time difference.

The explicit expression of classical time correlation function is,
$C_(t) = \int d^N \mathbf d^N \mathbf f(\mathbf_0, \mathbf_0) A(\mathbf_0, \mathbf_0) B(\mathbf_t, \mathbf_t)$
where $A(\mathbf_0, \mathbf_0)$ is the value of $A$ at time $t=0$, $B(\mathbf_t, \mathbf_t)$ is the value of $B$ at time $t$ given the initial state $(\mathbf_0, \mathbf_0)$, and $f(\mathbf_0, \mathbf_0)$ is the phase space distribution function for the initial state. If the ergodicity is assumed, then the ensemble average is the same as time average in a long time; mathematically,
$C_(\tau) = \langle A(\tau) B(0) \rangle = \lim_ \frac \int_0^ dt \, A(t+\tau) B(t)$
scanning different time window $\tau$ gives the time correlation function. As $t \to 0$, the correlation function $C_(0) = \langle A B \rangle$, while as $t \to \infty$, we may assume the correlation vanishes and $\lim_ C_(t) = \langle A \rangle \langle B \rangle$.

Correspondingly, the quantum time correlation function is, in the canonical ensemble,
C_(t) = \frac \text\left ^ \hat e^ \hat e^\right/math>
where $\hat$ and $\hat$ are the quantum operator, and $\hat(t) = e^ \hat(0) e^$ in the Heisenberg picture. If evaluating the (non-symmetrized) quantum time correlation function by expanding the trace to the eigenstates,
$C_(t)=\frac \sum_ e^ e^ A_ B_$
Evaluating quantum time correlation function quantum mechanically is very expensive, and this cannot be applied to a large system with many degrees of freedom. Nevertheless, semiclassical initial value representation (SC-IVR) is a family to evaluate the quantum time correlation function from the definition.

Additionally, there are two alternative quantum time correlations, and they both related to the definition of quantum time correlation function in the Fourier space. The first symmetrized correlation function $G_(t)$ is defined by,
G_(t) = \frac \text \left hat e^ \hat e^\right/math>
with $\tau_c \equiv t - i\beta \hbar / 2$ as a complex time variable. $G_(t)$ is related with the definition of quantum time correlation function by,
$\tilde_(\omega) = e^ \tilde_(\omega)$
The second symmetrized (Kubo transformed) correlation function is,
K_(t) = \frac \int_0^ d\lambda \operatorname \left ^ \hat e^ e^ \hat e^\right/math>
and $K_(t)$ reduces to its classical counterpart both in the high temperature and harmonic limit. $K_(t)$ is related with the definition of quantum time correlation function by,
\tilde_(\omega) = \left frac\right\tilde_(\omega)
The symmetrized quantum time correlation function are easier to evaluate, and the Fourier transformed relation makes them applicable in calculating spectrum, transport coefficients, etc. Quantum time correlation function can be approximated using the path integral molecular dynamics.

Generalization beyond equilibrium correlation functions

All of the above correlation functions have been defined in the context of equilibrium statistical mechanics. However, it is possible to define correlation functions for systems away from equilibrium. Examining the general definition of $C(r,\tau)$, it is clear that one can define the random variables used in these correlation functions, such as atomic positions and spins, away from equilibrium. As such, their scalar product is well-defined away from equilibrium. The operation which is no longer well-defined away from equilibrium is the average over the equilibrium ensemble. This averaging process for non-equilibrium system is typically replaced by averaging the scalar product across the entire sample. This is typical in scattering experiments and computer simulations, and is often used to measure the radial distribution functions of glasses.

One can also define averages over states for systems perturbed slightly from equilibrium. See, for example, http://xbeams.chem.yale.edu/~batista/vaa/node56.html

Measuring correlation functions

Correlation functions are typically measured with scattering experiments. For example, x-ray scattering experiments directly measure electron-electron equal-time correlations. From knowledge of elemental structure factors, one can also measure elemental pair correlation functions. See Radial distribution function for further information. Equal-time spin–spin correlation functions are measured with neutron scattering as opposed to x-ray scattering. Neutron scattering can also yield information on pair correlations as well. For systems composed of particles larger than about one micrometer, optical microscopy can be used to measure both equal-time and equal-position correlation functions. Optical microscopy is thus common for colloidal suspensions, especially in two dimensions.

Time evolution of correlation functions

In 1931, Lars Onsager proposed that the regression of microscopic thermal fluctuations at equilibrium follows the macroscopic law of relaxation of small non-equilibrium disturbances. This is known as the '' Onsager regression hypothesis''. As the values of microscopic variables separated by large timescales, $\tau$, should be uncorrelated beyond what we would expect from thermodynamic equilibrium, the evolution in time of a correlation function can be viewed from a physical standpoint as the system gradually 'forgetting' the initial conditions placed upon it via the specification of some microscopic variable. There is actually an intuitive connection between the time evolution of correlation functions and the time evolution of macroscopic systems: on average, the correlation function evolves in time in the same manner as if a system was prepared in the conditions specified by the correlation function's initial value and allowed to evolve.

Equilibrium fluctuations of the system can be related to its response to external perturbations via the Fluctuation-dissipation theorem.

The connection between phase transitions and correlation functions

Continuous phase transitions, such as order-disorder transitions in metallic alloys and ferromagnetic-paramagnetic transitions, involve a transition from an ordered to a disordered state. In terms of correlation functions, the equal-time correlation function is non-zero for all lattice points below the critical temperature, and is non-negligible for only a fairly small radius above the critical temperature. As the phase transition is continuous, the length over which the microscopic variables are correlated, $\xi$, must transition continuously from being infinite to finite when the material is heated through its critical temperature. This gives rise to a power-law dependence of the correlation function as a function of distance at the critical point. This is shown in the figure in the left for the case of a ferromagnetic material, with the quantitative details listed in the section on magnetism.

Applications

Magnetism

In a spin system, the equal-time correlation function is especially well-studied. It describes the canonical ensemble (thermal) average of the scalar product of the spins at two lattice points over all possible orderings:
$C (r) = \langle \mathbf(R) \cdot \mathbf(R+r)\rangle\ - \langle \mathbf(R) \rangle\langle \mathbf(R+r) \rangle\,.$
Here the brackets mean the above-mentioned thermal average. Schematic plots of this function are shown for a ferromagnetic material below, at, and above its Curie temperature on the left.

Even in a magnetically disordered phase, spins at different positions are correlated, i.e., if the distance r is very small (compared to some length scale $\xi$), the interaction between the spins will cause them to be correlated.
The alignment that would naturally arise as a result of the interaction between spins is destroyed by thermal effects. At high temperatures exponentially-decaying correlations are observed with increasing distance, with the correlation function being given asymptotically by
:$C (r) \approx \frac\exp\,,$
where r is the distance between spins, and d is the dimension of the system, and $\vartheta$ is an exponent, whose value depends on whether the system is in the disordered phase (i.e. above the critical point), or in the ordered phase (i.e. below the critical point). At high temperatures, the correlation decays to zero exponentially with the distance between the spins. The same exponential decay as a function of radial distance is also observed below $T_c$, but with the limit at large distances being the mean magnetization $\langle M^2 \rangle$. Precisely at the critical point, an algebraic behavior is seen
:$C (r) \approx \frac\,,$
where $\eta$ is a critical exponent, which does not have any simple relation with the non-critical exponent $\vartheta$ introduced above.
For example, the exact solution of the two-dimensional Ising model (with short-ranged ferromagnetic interactions) gives precisely at criticality $\eta = \frac$, but above criticality $\vartheta = \frac$ and below criticality $\vartheta = 2$.

As the temperature is lowered, thermal disordering is lowered, and in a continuous phase transition the correlation length diverges, as the correlation length must transition continuously from a finite value above the phase transition, to infinite below the phase transition:

:$\xi\propto , T-T_c, ^\,,$

with another critical exponent $\nu$.

This power law correlation is responsible for the scaling, seen in these transitions. All exponents mentioned are independent of temperature.
They are in fact universal, i.e. found to be the same in a wide variety of systems.

Radial distribution functions

One common correlation function is the radial distribution function which is seen often in statistical mechanics and fluid mechanics. The correlation function can be calculated in exactly solvable models (one-dimensional Bose gas, spin chains, Hubbard model) by means of Quantum inverse scattering method and Bethe ansatz. In an isotropic XY model, time and temperature correlations were evaluated by Its, Korepin, Izergin & Slavnov.

Higher order correlation functions

Higher-order correlation functions involve multiple reference points, and are defined through a generalization of the above correlation function by taking the expected value of the product of more than two random variables:

:$C_(s_1,s_2,\cdots,s_n) = \langle X_(s_1) X_(s_2) \cdots X_(s_n)\rangle.$

However, such higher order correlation functions are relatively difficult to interpret and measure. For example, in order to measure the higher-order analogues of pair distribution functions, coherent x-ray sources are needed. Both the theory of such analysis and the experimental measurement of the needed X-ray cross-correlation functions are areas of active research.

See also

* Ornstein–Zernike equation

References

Further reading

*
*Radial distribution function
*
* {{cite journal , author-link=Michael E. Fisher , first=M. E. , last=Fisher , title=Renormalization Group in Theory of Critical Behavior , journal=Reviews of Modern Physics , volume=46 , issue=4 , pages=597–616 , year=1974 , doi=10.1103/RevModPhys.46.597 , bibcode = 1974RvMP...46..597F
* C. Domb, M.S. Green, J.L. Lebowitz editors, '' Phase Transitions and Critical Phenomena'', vol. 1-20 (1972–2001), Academic Press.

Covariance and correlation
Statistical mechanics
Conceptual models