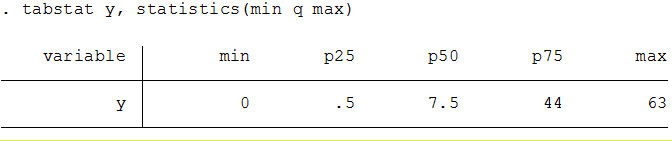|
Triangular Distribution
In probability theory and statistics, the triangular distribution is a continuous probability distribution with lower limit ''a'', upper limit ''b'' and mode ''c'', where ''a'' < ''b'' and ''a'' ≤ ''c'' ≤ ''b''. Special cases Mode at a bound The distribution simplifies when ''c'' = ''a'' or ''c'' = ''b''. For example, if ''a'' = 0, ''b'' = 1 and ''c'' = 1, then the and CDF become: : : |
Triangular Distribution PMF
A triangle is a polygon with three Edge (geometry), edges and three Vertex (geometry), vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC. In Euclidean geometry, any three points, when non-Collinearity, collinear, determine a unique triangle and simultaneously, a unique Plane (mathematics), plane (i.e. a two-dimensional Euclidean space). In other words, there is only one plane that contains that triangle, and every triangle is contained in some plane. If the entire geometry is only the Euclidean plane, there is only one plane and all triangles are contained in it; however, in higher-dimensional Euclidean spaces, this is no longer true. This article is about triangles in Euclidean geometry, and in particular, the Euclidean plane, except where otherwise noted. Types of triangle The terminology for categorizing triangles is more than two thousand years old, having been defined on the very first page of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
PERT Distribution
In probability and statistics, the PERT distribution is a family of continuous probability distributions defined by the minimum (a), most likely (b) and maximum (c) values that a variable can take. It is a transformation of the four-parameter beta distribution with an additional assumption that its expected value is : \mu = \frac 6. The mean of the distribution is therefore defined as the weighted average of the minimum, most likely and maximum values that the variable may take, with four times the weight applied to the most likely value. This assumption about the mean was first proposed in Clark, 1962 for estimating the effect of uncertainty of task durations on the outcome of a project schedule being evaluated using the program evaluation and review technique, hence its name. The mathematics of the distribution resulted from the authors' desire to make the standard deviation equal to about 1/6 of the range. The PERT distribution is widely used in risk analysis to represent the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Central Limit Theorem
In probability theory, the central limit theorem (CLT) establishes that, in many situations, when independent random variables are summed up, their properly normalized sum tends toward a normal distribution even if the original variables themselves are not normally distributed. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions. This theorem has seen many changes during the formal development of probability theory. Previous versions of the theorem date back to 1811, but in its modern general form, this fundamental result in probability theory was precisely stated as late as 1920, thereby serving as a bridge between classical and modern probability theory. If X_1, X_2, \dots, X_n, \dots are random samples drawn from a population with overall mean \mu and finite variance and if \bar_n is the sample mean of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Function
A triangular function (also known as a triangle function, hat function, or tent function) is a function whose graph takes the shape of a triangle. Often this is an isosceles triangle of height 1 and base 2 in which case it is referred to as ''the'' triangular function. Triangular functions are useful in signal processing and ''communication systems engineering'' as representations of idealized signals, and the triangular function specifically as an integral transform kernel function from which more realistic signals can be derived, for example in kernel density estimation. It also has applications in pulse-code modulation as a pulse shape for transmitting digital signals and as a matched filter for receiving the signals. It is also used to define the triangular window sometimes called the Bartlett window. Definitions The most common definition is as a piecewise function: : \begin \operatorname(x) = \Lambda(x) \ &\overset \ \max\big(1 - , x, , 0\big) \\ &= \begin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seven-number Summary
In descriptive statistics, the seven-number summary is a collection of seven summary statistics, and is an extension of the five-number summary. There are three similar, common forms. As with the five-number summary, it can be represented by a modified box plot, adding hatch-marks on the "whiskers" for two of the additional numbers. Seven-number summary The following percentiles are (approximately) evenly spaced under a normally distributed variable: # the 2nd percentile (better: 2.15%) # the 9th percentile (better: 8.87%) # the 25th percentile or lower quartile or ''first quartile'' # the 50th percentile or median (middle value, or ''second quartile'') # the 75th percentile or upper quartile or ''third quartile'' # the 91st percentile (better: 91.13%) # the 98th percentile (better: 97.85%) The middle three values – the lower quartile, median, and upper quartile – are the usual statistics from the five-number summary and are the standard values for the box in a box ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Five-number Summary
The five-number summary is a set of descriptive statistics that provides information about a dataset. It consists of the five most important sample percentiles: # the sample minimum ''(smallest observation)'' # the lower quartile or ''first quartile'' # the median (the middle value) # the upper quartile or ''third quartile'' # the sample maximum (largest observation) In addition to the median of a single set of data there are two related statistics called the upper and lower quartiles. If data are placed in order, then the lower quartile is central to the lower half of the data and the upper quartile is central to the upper half of the data. These quartiles are used to calculate the interquartile range, which helps to describe the spread of the data, and determine whether or not any data points are outliers. In order for these statistics to exist the observations must be from a univariate variable that can be measured on an ordinal, interval or ratio scale. Use and representa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-point Estimation
The three-point estimation technique is used in management and information systems applications for the construction of an approximate probability distribution representing the outcome of future events, based on very limited information. While the distribution used for the approximation might be a normal distribution, this is not always so. For example, a triangular distribution might be used, depending on the application. In three-point estimation, three figures are produced initially for every distribution that is required, based on prior experience or best-guesses: * ''a'' = the best-case estimate * ''m'' = the most likely estimate * ''b'' = the worst-case estimate These are then combined to yield either a full probability distribution, for later combination with distributions obtained similarly for other variables, or summary descriptors of the distribution, such as the mean, standard deviation or percentage points of the distribution. The accuracy attributed to the results deriv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thomas Simpson
Thomas Simpson Fellow of the Royal Society, FRS (20 August 1710 – 14 May 1761) was a British mathematician and inventor known for the :wikt:eponym, eponymous Simpson's rule to approximate definite integrals. The attribution, as often in mathematics, can be debated: this rule had been found 100 years earlier by Johannes Kepler, and in German it is called :de:Keplersche Fassregel, Keplersche Fassregel. Biography Simpson was born in Sutton Cheney, Leicestershire. The son of a weaver, Simpson taught himself mathematics. At the age of nineteen, he married a fifty-year old widow with two children. As a youth, he became interested in astrology after seeing a solar eclipse. He also dabbled in divination and caused fits in a girl after 'raising a devil' from her. After this incident, he and his wife had to flee to Derby. He moved with his wife and children to London at age twenty-five, where he supported his family by weaving during the day and teaching mathematics at night. From 17 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
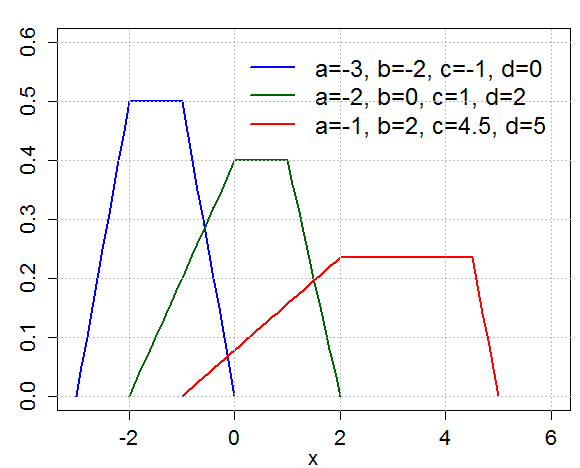
Trapezoidal Distribution
In probability theory and statistics, the trapezoidal distribution is a continuous probability distribution whose probability density function graph resembles a trapezoid. Likewise, trapezoidal distributions also roughly resemble mesas or plateaus. Each trapezoidal distribution has a lower bound and an upper bound , where , beyond which no values or events on the distribution can occur (i.e. beyond which the probability is always zero). In addition, there are two sharp bending points (non-differentiable discontinuities) within the probability distribution, which we will call and , which occur between and , such that . The image to the right shows a perfectly linear trapezoidal distribution. However, not all trapezoidal distributions are so precisely shaped. In the standard case, where the middle part of the trapezoid is completely flat, and the side ramps are perfectly linear, all of the values between and will occur with equal frequency, and therefore all such points will ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dither
Dither is an intentionally applied form of image noise, noise used to randomize quantization error, preventing large-scale patterns such as color banding in images. Dither is routinely used in processing of both digital audio and digital video, video data, and is often one of the last stages of Audio mastering, mastering audio to a compact disc, CD. A common use of dither is converting a grayscale image to Binary image, black and white, such that the density of black dots in the new image approximates the average gray level in the original. Etymology The term ''dither'' was published in books on analog computation and hydraulically controlled guns shortly after World War II. Though he did not use the term ''dither'', the concept of dithering to reduce quantization patterns was first applied by Lawrence G. Roberts in his 1961 MIT master's thesis and 1962 article. By 1964 dither was being used in the modern sense described in this article. The technique was in use at least ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
PERT
Pert or PERT may refer to: Ships * - see List of United States Navy ships: P * , a World War II corvette, originally HMS ''Nepeta'' * ''Pert'' (sidewheeler), a 19th-century steamboat that operated in British Columbia, Canada Statistics * PERT distribution People * Pert (surname) * Pert Kelton (1907–1968), American actress PERT * Program evaluation and review technique, or PERT Chart, a planning method * Postsecondary Education Readiness Test, a placement test used by Florida high schools and colleges Other uses * Pert Plus, a brand of shampoo marketed in Australia and New Zealand as Pert * P e ^ , an expression to calculate the expected return from a continuously compounded investment given the principal, rate, and time See also * Peart Peart is the surname of: *Alan Peart (1922–2018), New Zealand Second World War flying ace * Bob Peart (1926–1966), English football player *Charles Peart (1759–1798), British sculptor * Darrell Peart (born 1950), American furnitu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
