|
Subpaving
In mathematics, a subpaving is a set of nonoverlapping boxes of R⁺. A subset ''X'' of Rⁿ can be approximated by two subpavings ''X⁻'' and ''X⁺'' such that ''X⁻'' ⊂ ''X'' ⊂ ''X⁺''. In R¹ the boxes are line segments, in R² rectangles and in Rⁿ hyperrectangles. A R² subpaving can be also a " non-regular tiling by rectangles", when it has no holes. Boxes present the advantage of being very easily manipulated by computers, as they form the heart of interval analysis. Many interval algorithms naturally provide solutions that are regular subpavings. In computation, a well-known application of subpaving in R² is the Quadtree data structure. In image tracing context and other applications is important to see ''X⁻'' as topological interior, as illustrated. Example The three figures on the right below show an approximation of the set ''X'' = with different accuracies. The set ''X⁻'' corresponds to red boxes and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Image Tracing
In computer graphics, image tracing, raster-to-vector conversion or raster vectorization is the conversion of raster graphics into vector graphics. Background An image does not have any structure: it is just a collection of marks on paper, grains in film, or pixels in a bitmap. While such an image is useful, it has some limits. If the image is magnified enough, its artifacts appear. The halftone dots, film grains, and pixels become apparent. Images of sharp edges become fuzzy or jagged. See, for example, pixelation. Ideally, a vector image does not have the same problem. Edges and filled areas are represented as mathematical curves or gradients, and they can be magnified arbitrarily (though of course the final image must also be rasterized in to be rendered, and its quality depends on the quality of the rasterization algorithm for the given inputs). The task in vectorization is to convert a two-dimensional image into a two-dimensional vector representation of the image. It is not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadtree
A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are the two-dimensional analog of octrees and are most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The data associated with a leaf cell varies by application, but the leaf cell represents a "unit of interesting spatial information". The subdivided regions may be square or rectangular, or may have arbitrary shapes. This data structure was named a quadtree by Raphael Finkel and J.L. Bentley in 1974. A similar partitioning is also known as a ''Q-tree''. All forms of quadtrees share some common features: * They decompose space into adaptable cells * Each cell (or bucket) has a maximum capacity. When maximum capacity is reached, the bucket splits * The tree directory follows the spatial decomposition of the quadtree. A tree-pyramid (T-pyramid) is a "complete" tree; every node of the T-pyramid has four child nodes excep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
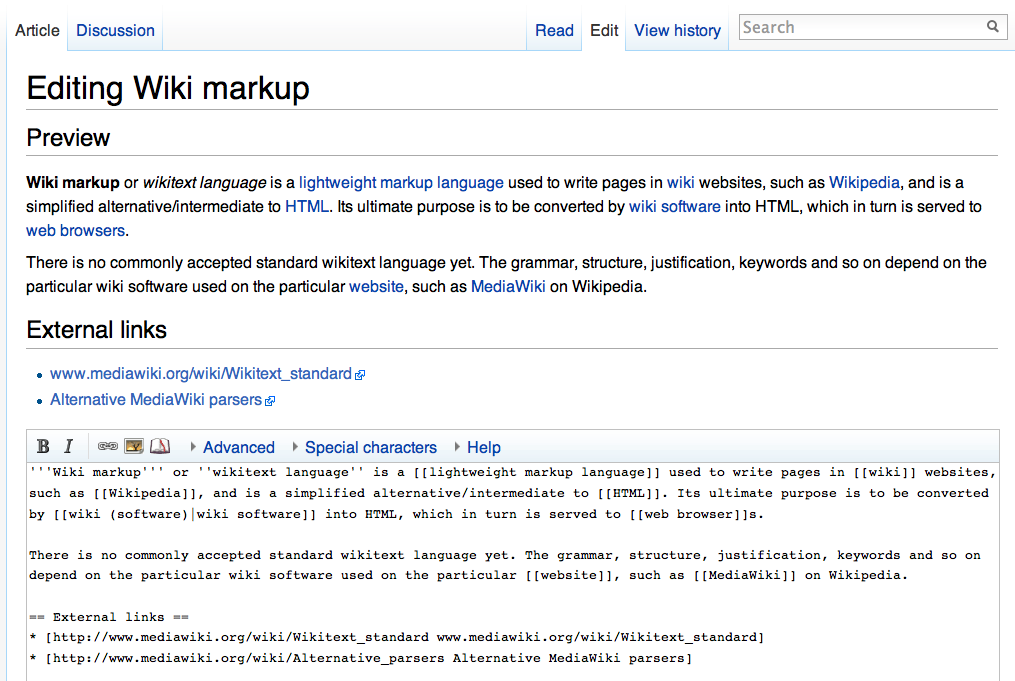
Wiki Subpaving2
A wiki ( ) is an online hypertext publication collaboratively edited and managed by its own audience, using a web browser. A typical wiki contains multiple pages for the subjects or scope of the project, and could be either open to the public or limited to use within an organization for maintaining its internal knowledge base. Wikis are enabled by wiki software, otherwise known as wiki engines. A wiki engine, being a form of a content management system, differs from other web-based systems such as blog software, in that the content is created without any defined owner or leader, and wikis have little inherent structure, allowing structure to emerge according to the needs of the users. Wiki engines usually allow content to be written using a simplified markup language and sometimes edited with the help of a rich-text editor. There are dozens of different wiki engines in use, both standalone and part of other software, such as bug tracking systems. Some wiki engines are ope ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Motion Planning
Motion planning, also path planning (also known as the navigation problem or the piano mover's problem) is a computational problem to find a sequence of valid configurations that moves the object from the source to destination. The term is used in computational geometry, computer animation, robotics and computer games. For example, consider navigating a mobile robot inside a building to a distant waypoint. It should execute this task while avoiding walls and not falling down stairs. A motion planning algorithm would take a description of these tasks as input, and produce the speed and turning commands sent to the robot's wheels. Motion planning algorithms might address robots with a larger number of joints (e.g., industrial manipulators), more complex tasks (e.g. manipulation of objects), different constraints (e.g., a car that can only drive forward), and uncertainty (e.g. imperfect models of the environment or robot). Motion planning has several robotics applications, such ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topology
In mathematics, topology (from the Greek language, Greek words , and ) is concerned with the properties of a mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformations, such as Stretch factor, stretching, Twist (mathematics), twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a set (mathematics), set endowed with a structure, called a ''Topology (structure), topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of continuity (mathematics), continuity. Euclidean spaces, and, more generally, metric spaces are examples of a topological space, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and homotopy, homotopies. A property that is invariant under such deformations is a topological property. Basic exampl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Path Connected
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint non-empty open subsets. Connectedness is one of the principal topological properties that are used to distinguish topological spaces. A subset of a topological space X is a if it is a connected space when viewed as a subspace of X. Some related but stronger conditions are path connected, simply connected, and n-connected. Another related notion is ''locally connected'', which neither implies nor follows from connectedness. Formal definition A topological space X is said to be if it is the union of two disjoint non-empty open sets. Otherwise, X is said to be connected. A subset of a topological space is said to be connected if it is connected under its subspace topology. Some authors exclude the empty set (with its unique topology) as a connected space, but this article does not follow that practice. For a topologic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inequality (mathematics)
In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions. It is used most often to compare two numbers on the number line by their size. There are several different notations used to represent different kinds of inequalities: * The notation ''a'' ''b'' means that ''a'' is greater than ''b''. In either case, ''a'' is not equal to ''b''. These relations are known as strict inequalities, meaning that ''a'' is strictly less than or strictly greater than ''b''. Equivalence is excluded. In contrast to strict inequalities, there are two types of inequality relations that are not strict: * The notation ''a'' ≤ ''b'' or ''a'' ⩽ ''b'' means that ''a'' is less than or equal to ''b'' (or, equivalently, at most ''b'', or not greater than ''b''). * The notation ''a'' ≥ ''b'' or ''a'' ⩾ ''b'' means that ''a'' is greater than or equal to ''b'' (or, equivalently, at least ''b'', or not less than ''b''). The re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set Inversion
In mathematics, set inversion is the problem of characterizing the preimage ''X'' of a set ''Y'' by a function ''f'', i.e., ''X'' = ''f'' −1(''Y'' ) = . It can also be viewed as the problem of describing the solution set of the quantified constraint "''Y''(''f'' (''x''))", where ''Y''( ''y'') is a constraint, e.g. an inequality, describing the set ''Y''. In most applications, ''f'' is a function from R''n'' to R''p'' and the set ''Y'' is a box of R''p'' (i.e. a Cartesian product of ''p'' intervals of R). When ''f'' is nonlinear the set inversion problem can be solved using interval analysis combined with a branch-and-bound algorithm. The main idea consists in building a paving of R''p'' made with non-overlapping boxes. For each box 'x'' we perform the following tests: # if ''f'' ( 'x'' ⊂ ''Y'' we conclude that 'x''⊂ ''X''; # if ''f'' ( 'x'' ∩ ''Y'' = ∅ we conclude that 'x''∩ ''X'' = ∅; # Otherwise, the box 'x''t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wiki Subpaving3
A wiki ( ) is an online hypertext publication Collaborative editing, collaboratively edited and managed by its own audience, using a web browser. A typical wiki contains multiple pages for the subjects or scope of the project, and could be either open to the public or limited to use within an organization for maintaining its internal knowledge base. Wikis are enabled by wiki software, otherwise known as wiki engines. A wiki engine, being a form of a content management system, differs from other web application, web-based systems such as blog software, in that the content is created without any defined owner or leader, and wikis have little inherent structure, allowing structure to emerge according to the needs of the users. Wiki engines usually allow content to be written using a simplified markup language and sometimes edited with the help of a Online rich-text editor, rich-text editor. There are dozens of different wiki engines in use, both standalone and part of other sof ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interior (topology)
In mathematics, specifically in general topology, topology, the interior of a subset of a topological space is the Union (set theory), union of all subsets of that are Open set, open in . A point that is in the interior of is an interior point of . The interior of is the Absolute complement, complement of the closure (topology), closure of the complement of . In this sense interior and closure are Duality_(mathematics)#Duality_in_logic_and_set_theory, dual notions. The exterior of a set is the complement of the closure of ; it consists of the points that are in neither the set nor its boundary (topology), boundary. The interior, boundary, and exterior of a subset together partition of a set, partition the whole space into three blocks (or fewer when one or more of these is empty set, empty). Definitions Interior point If is a subset of a Euclidean space, then is an interior point of if there exists an open ball centered at which is completely contained in . (This is i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wiki Subpaving1
A wiki ( ) is an online hypertext publication collaboratively edited and managed by its own audience, using a web browser. A typical wiki contains multiple pages for the subjects or scope of the project, and could be either open to the public or limited to use within an organization for maintaining its internal knowledge base. Wikis are enabled by wiki software, otherwise known as wiki engines. A wiki engine, being a form of a content management system, differs from other web-based systems such as blog software, in that the content is created without any defined owner or leader, and wikis have little inherent structure, allowing structure to emerge according to the needs of the users. Wiki engines usually allow content to be written using a simplified markup language and sometimes edited with the help of a rich-text editor. There are dozens of different wiki engines in use, both standalone and part of other software, such as bug tracking systems. Some wiki engines are ope ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
