|
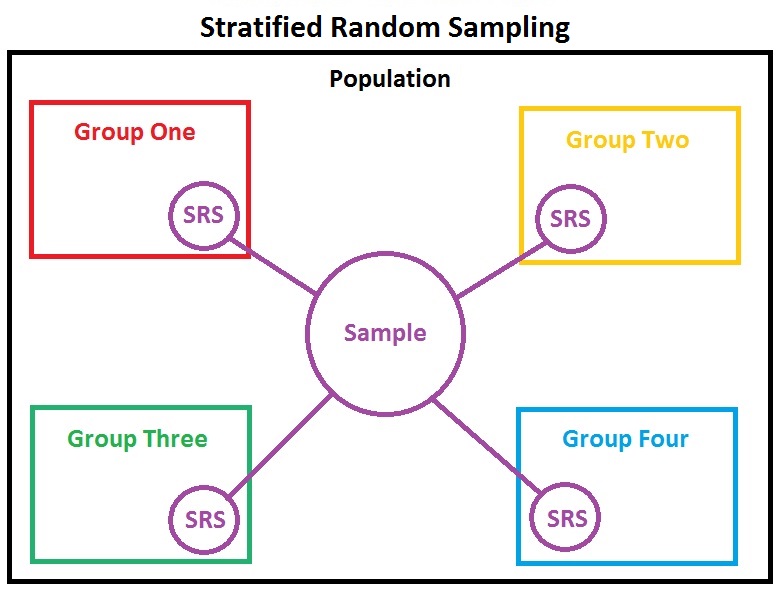
Stratified Randomization
In statistics, stratified randomization is a method of Sampling (statistics), sampling which first stratifies the whole study Statistical population, population into Statistical population, subgroups with same Variable and attribute (research), attributes or characteristics, known as strata, then followed by Simple random sample, simple random sampling from the stratified groups, where each element within the same subgroup are selected Bias (statistics), unbiasedly during any stage of the sampling process, randomly and entirely by chance. Stratified randomization is considered a subdivision of stratified sampling, and should be adopted when shared attributes exist partially and vary widely between subgroups of the investigated population, so that they require special considerations or clear distinctions during sampling. This sampling method should be distinguished from cluster sampling, where a simple random sample of several entire clusters is selected to represent the whole popula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coverage Probability
In statistical estimation theory, the coverage probability, or coverage for short, is the probability that a confidence interval or confidence region will include the true value (parameter) of interest. It can be defined as the proportion of instances where the interval surrounds the true value as assessed by long-run frequency. In statistical prediction, the coverage probability is the probability that a prediction interval will include an out-of-sample value of the random variable. The coverage probability can be defined as the proportion of instances where the interval surrounds an out-of-sample value as assessed by long-run frequency. Concept The fixed degree of certainty pre-specified by the analyst, referred to as the ''confidence level'' or ''confidence coefficient'' of the constructed interval, is effectively the nominal coverage probability of the procedure for constructing confidence intervals. Hence, referring to a "nominal confidence level" or "nominal confi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Confounding
In causal inference, a confounder is a variable that influences both the dependent variable and independent variable, causing a spurious association. Confounding is a causal concept, and as such, cannot be described in terms of correlations or associations.Pearl, J., (2009). Simpson's Paradox, Confounding, and Collapsibility In ''Causality: Models, Reasoning and Inference'' (2nd ed.). New York : Cambridge University Press. The existence of confounders is an important quantitative explanation why correlation does not imply causation. Some notations are explicitly designed to identify the existence, possible existence, or non-existence of confounders in causal relationships between elements of a system. Confounders are threats to internal validity. Example Let's assume that a trucking company owns a fleet of trucks made by two different manufacturers. Trucks made by one manufacturer are called "A Trucks" and trucks made by the other manufacturer are called "B Trucks." ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Association (statistics)
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weighting
The process of frequency weighting involves emphasizing the contribution of particular aspects of a phenomenon (or of a set of data) over others to an outcome or result; thereby highlighting those aspects in comparison to others in the analysis. That is, rather than each variable in the data set contributing equally to the final result, some of the data is adjusted to make a greater contribution than others. This is analogous to the practice of adding (extra) weight to one side of a pair of scales in order to favour either the buyer or seller. While weighting may be applied to a set of data, such as epidemiological data, it is more commonly applied to measurements of light, heat, sound, gamma radiation, and in fact any stimulus that is spread over a spectrum A spectrum (: spectra or spectrums) is a set of related ideas, objects, or properties whose features overlap such that they blend to form a continuum. The word ''spectrum'' was first used scientifically in optics t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clinical Trial
Clinical trials are prospective biomedical or behavioral research studies on human subject research, human participants designed to answer specific questions about biomedical or behavioral interventions, including new treatments (such as novel vaccines, pharmaceutical drug, drugs, medical nutrition therapy, dietary choices, dietary supplements, and medical devices) and known interventions that warrant further study and comparison. Clinical trials generate data on dosage, safety and efficacy. They are conducted only after they have received institutional review board, health authority/ethics committee approval in the country where approval of the therapy is sought. These authorities are responsible for vetting the risk/benefit ratio of the trial—their approval does not mean the therapy is 'safe' or effective, only that the trial may be conducted. Depending on product type and development stage, investigators initially enroll volunteers or patients into small Pilot experiment, pi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Randomized Block Design
In the statistical theory of the design of experiments, blocking is the arranging of experimental units that are similar to one another in groups (blocks) based on one or more variables. These variables are chosen carefully to minimize the effect of their variability on the observed outcomes. There are different ways that blocking can be implemented, resulting in different confounding effects. However, the different methods share the same purpose: to control variability introduced by specific factors that could influence the outcome of an experiment. The roots of blocking originated from the statistician, Ronald Fisher, following his development of ANOVA. History The use of blocking in experimental design has an evolving history that spans multiple disciplines. The foundational concepts of blocking date back to the early 20th century with statisticians like Ronald A. Fisher. His work in developing analysis of variance (ANOVA) set the groundwork for grouping experimental units ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimisation (clinical Trials)
Minimisation is a method of adaptive stratified sampling that is used in clinical trials Clinical trials are prospective biomedical or behavioral research studies on human subject research, human participants designed to answer specific questions about biomedical or behavioral interventions, including new treatments (such as novel v ..., as described by Pocock and Simon. The aim of minimisation is to minimise the imbalance between the number of patients in each treatment group over a number of factors. Normally patients would be allocated to a treatment group randomly and while this maintains a good overall balance, it can lead to imbalances within sub-groups. For example, if a majority of the patients who were receiving the active drug happened to be male, or smokers, the statistical usefulness of the study would be reduced. The traditional method to avoid this problem, known as blocked randomisation, is to stratify patients according to a number of factors (e.g. male an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Blocking (statistics)
In the statistical theory of the design of experiments, blocking is the arranging of experimental units that are similar to one another in groups (blocks) based on one or more variables. These variables are chosen carefully to minimize the effect of their variability on the observed outcomes. There are different ways that blocking can be implemented, resulting in different confounding effects. However, the different methods share the same purpose: to control variability introduced by specific factors that could influence the outcome of an experiment. The roots of blocking originated from the statistician, Ronald Fisher, following his development of Analysis of variance, ANOVA. History The use of blocking in experimental design has an evolving history that spans multiple disciplines. The foundational concepts of blocking date back to the early 20th century with statisticians like Ronald A. Fisher. His work in developing analysis of variance (ANOVA) set the groundwork for grouping ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Margin Of Error
The margin of error is a statistic expressing the amount of random sampling error in the results of a Statistical survey, survey. The larger the margin of error, the less confidence one should have that a poll result would reflect the result of a simultaneous census of the entire Statistical population, population. The margin of error will be positive whenever a population is incompletely sampled and the outcome measure has positive variance, which is to say, whenever the measure ''varies''. The term ''margin of error'' is often used in non-survey contexts to indicate observational error in reporting measured quantities. Concept Consider a simple ''yes/no'' poll P as a sample of n respondents drawn from a population N \text(n \ll N) reporting the percentage p of ''yes'' responses. We would like to know how close p is to the true result of a survey of the entire population N, without having to conduct one. If, hypothetically, we were to conduct a poll P over subsequent sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |