Stratified Randomization

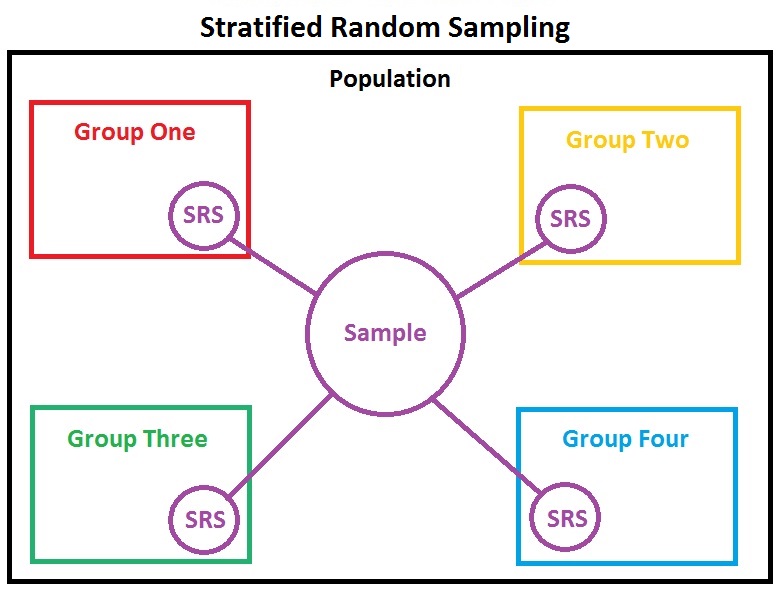
In statistics, stratified randomization is a method of sampling which first stratifies the whole study population into subgroups with same attributes or characteristics, known as strata, then followed by simple random sampling from the stratified groups, where each element within the same subgroup are selected unbiasedly during any stage of the sampling process, randomly and entirely by chance. Stratified randomization is considered a subdivision of stratified sampling, and should be adopted when shared attributes exist partially and vary widely between subgroups of the investigated population, so that they require special considerations or clear distinctions during sampling. This sampling method should be distinguished from cluster sampling, where a simple random sample of several entire clusters is selected to represent the whole population, or stratified systematic sampling, where a systematic sampling is carried out after the stratification process. Stratified random sampling is sometimes also known as "quota random sampling".

Steps for stratified random sampling

Stratified randomization is extremely useful when the target population is heterogeneous and effectively displays how the trends or characteristics under study differ between strata. When performing a stratified randomization, the following 8 steps should be taken:

# Define a target population.
# Define stratification variables and decide the number of strata to be created. The criteria for defining variables for stratification include age, socioeconomic status, nationality, race, education level and others and should be in line with the research objective. Ideally, 4-6 strata should be employed, as any increase in stratification variables will raise the probability for some of them to cancel out the impact of other variables.
# Use a sampling frame to evaluate all the elements in the target population. Make changes afterwards based on coverage and grouping.
# List all the elements and consider the sampling result. Each stratum should be mutually exclusive and add up to cover all members of the population, whilst each member of the population should fall into unique stratum, along with other members with minimum differences.
# Make decisions over the random sampling selection criteria. This can be done manually or with a designed computer program.
# Assign a random and unique number to all the elements followed by sorting these elements according to their number assigned.
# Review the size of each stratum and numerical distribution of all elements in every strata. Determine the type of sampling, either proportional or disproportional stratified sampling.
# Carry out the selected random sampling as defined in step 5. At minimum, one element must be chosen from each stratum so that the final sample includes representatives from every stratum. If two or more elements from each stratum are selected, error margins of the collected data can be calculated.

Stratified random assignment

Stratified randomization may also refer to the random assignment of treatments to subjects, in addition to referring to random sampling of subjects from a population, as described above.

In this context, stratified randomization uses one or multiple prognostic factors to make subgroups, on average, that have similar entry characteristics. The patient factor can be accurately decided by examining the outcome in previous studies.

The number of subgroups can be calculated by multiplying the number of strata for each factor.  Factors are measured before or at the time of randomization and experimental subjects are divided into several subgroups or strata according to the results of measurements.

Within each stratum, several randomization strategies can be applied, which involves simple randomization, blocked randomization, and minimization.

Simple randomization within strata

Simple randomization is considered as the easiest method for allocating subjects in each stratum. Subjects are assigned to each group purely randomly for every assignment. Even though it is easy to conduct, simple randomization is commonly applied in strata that contain more than 100 samples since a small sampling size would make assignment unequal.

Block randomization within strata

Block randomization, sometimes called permuted block randomization, applies blocks to allocate subjects from the same strata equally to each group in the study. In block randomization, allocation ratio (ratio of the number of one specific group over other groups) and group sizes are specified. The block size must be the multiples of the number of treatments so that samples in each stratum can be assigned to treatment groups with the intended ratio. For instance, there should be 4 or 8 strata in a clinical trial concerning breast cancer where age and nodal statuses are two prognostic factors and each factor is split into two-level. The different blocks can be assigned to samples in multiple ways including random list and computer programming.

Block randomization is commonly used in the experiment with a relatively big sampling size to avoid the imbalance allocation of samples with important characteristics. In certain fields with strict requests of randomization such as clinical trials, the allocation would be predictable when there is no blinding process for conductors and the block size is limited. The blocks permuted randomization in strata could possibly cause an imbalance of samples among strata as the number of strata increases and the sample size is limited, For instance, there is a possibility that no sample is found meeting the characteristic of certain strata.

Minimization method

In order to guarantee the similarity of each treatment group, the "minimization" method attempts are made, which is more direct than random permuted block within strats. In the minimization method, samples in each stratum are assigned to treatment groups based on the sum of samples in each treatment group, which makes the number of subjects keep balance among the group. If the sums for multiple treatment groups are the same, simple randomization would be conducted to assign the treatment. In practice, the minimization method needs to follow a daily record of treatment assignments by prognostic factors, which can be done effectively by using a set of index cards to record.  The minimization method effectively avoids imbalance among groups but involves less random process than block randomization because the random process is only conducted when the treatment sums are the same. A feasible solution is to apply an additional random list which makes the treatment groups with a smaller sum of marginal totals possess a higher chance (e.g.¾) while other treatments have a lower chance(e.g.¼ ).

Application

Stratified random sampling is useful and productive in situations requiring different weightings on specific strata. In this way, the researchers can manipulate the selection mechanisms from each strata to amplify or minimize the desired characteristics in the survey result.

Stratified randomization is helpful when researchers intend to seek for associations between two or more strata, as simple random sampling causes a larger chance of unequal representation of target groups. It is also useful when the researchers wish to eliminate confounders in observational studies as stratified random sampling allows the adjustments of covariances and the ''p''-values for more accurate results.

There is also a higher level of statistical accuracy for stratified random sampling compared with simple random sampling, due to the high relevance of elements chosen to represent the population. The differences within the strata is much less compared to the one between strata. Hence, as the between-sample differences are minimized, the standard deviation will be consequently tightened, resulting in higher degree of accuracy and small error in the final results. This effectively reduces the sample size needed and increases cost-effectiveness of sampling when research funding is tight.

In real life, stratified random sampling can be applied to results of election polling, investigations into income disparities among social groups, or measurements of education opportunities across nations.

Stratified randomization in clinical trials

In clinical trials, patients are stratified according to their social and individual backgrounds, or any factor that are relevant to the study, to match each of these groups within the entire patient population. The aim of such is to create a balance of clinical/prognostic factor as the trials would not produce valid results if the study design is not balanced. The step of stratified randomization is extremely important as an attempt to ensure that no bias, delibrate or accidental, affects the representative nature of the patient sample under study. It increases the study power, especially in small clinical trials(n<400), as these known clinical traits stratified are thought to effect the outcomes of the interventions. It helps prevent the occurrence of type I error, which is valued highly in clinical studies. It also has an important effect on sample size for active control equivalence trials and in theory, facilitates subgroup analysis and interim analysis.

Advantage

The advantages of stratified randomization include:

# Stratified randomization can accurately reflect the outcomes of the general population since influential factors are applied to stratify the entire samples and balance the samples' vital characteristics among treatment groups. For instance, applying stratified randomization to make a sample of 100 from the population can guarantee the balance of males and females in each treatment group, while using simple randomization might result in only 20 males in one group and 80 males in another group.
# Stratified randomization makes a smaller error than other sampling methods such as cluster sampling, simple random sampling, and systematic sampling o
non-probability methods
since measurements within strata could be made to have a lower standard deviation. Randomizing divided strata are more manageable and cheaper in some cases than simply randomizing general samples.
# It is easier for a team to be trained to stratify a sample because of the exactness of the nature of stratified randomization.
# Researchers can get highly useful results by analyzing smaller sample sizes because of statistical accuracy of this method.
# This sampling technique covers a wide range of population since complete charge over the strata division has been made.
# Sometimes stratified randomization is desirable to have estimates of population parameters for groups within the population.

Disadvantage

The limits of stratified randomization include:

# Stratified randomization firstly divides samples into several strata with reference to prognostic factors but there is possible that the samples are unable to be divided. In application, the significance of prognostic factors lacks strict approval in some cases, which could further result in bias. This is why the factors' potential for making effects to result should be checked before the factors are included in stratification. In some cases that the impact of factors on the outcome cannot be approved, unstratified randomization is suggested.
# The subgroup size is taken to be of the same importance if the data available cannot represent overall subgroup population. In some applications, subgroup size is decided with reference to the amount of data available instead of scaling sample sizes to subgroup size, which would introduce bias in the effects of factors.  In some cases that data needs to be stratified by variances, subgroup variances differ significantly, making each subgroup sampling size proportional to the overall subgroup population cannot be guaranteed.
# Stratified sampling can not be applied if the population cannot be completely assigned into strata, which would result in sample sizes proportional to sample available instead of overall subgroup population.
# The process of assigning samples into subgroups could involve overlapping if subjects meet the inclusion standard of multiple strata, which could result in a misrepresentation of the population.

See also

* Sampling
* Simple random sampling
* Stratified sampling
* Stratification(clinical trials)
* Quota sampling
* Sample size determination
* Sampling error

References

{{Statistics

Sampling (statistics)
Sampling techniques