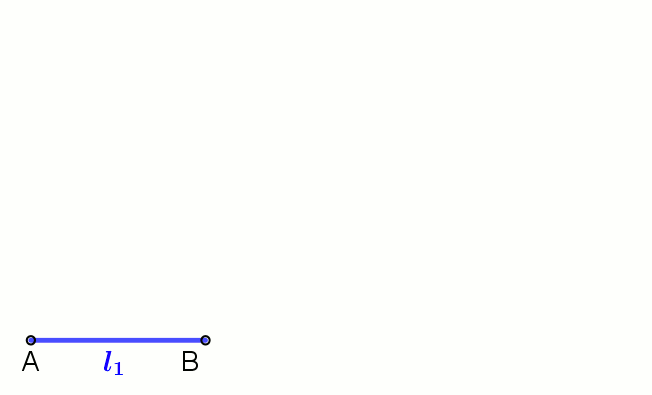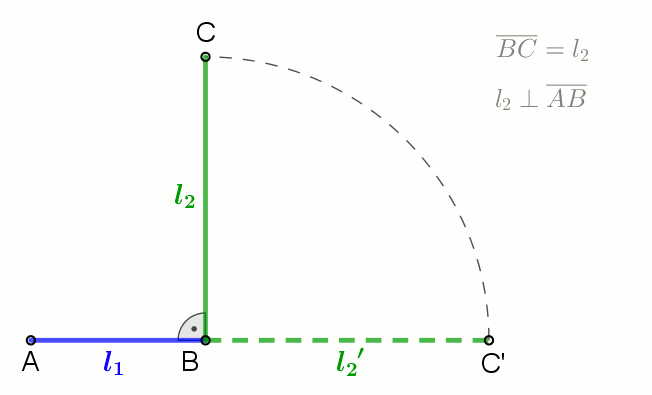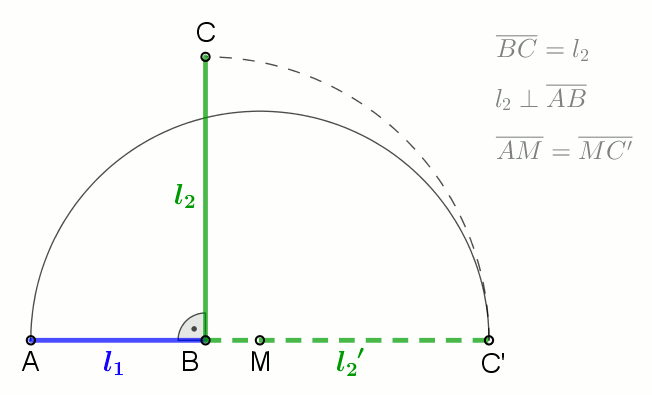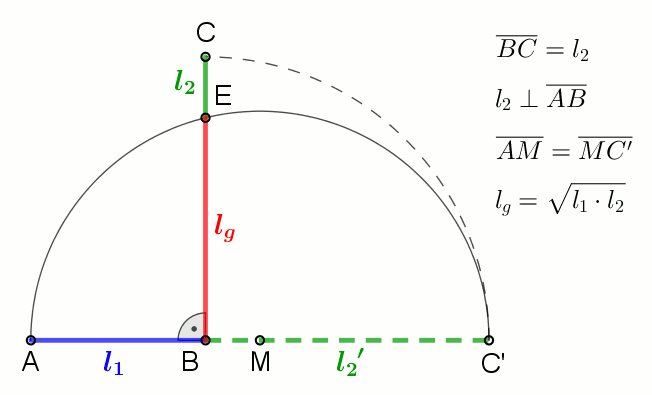|
Stolarsky Mean
In mathematics, the Stolarsky mean is a generalization of the logarithmic mean. It was introduced by Kenneth B. Stolarsky in 1975. Definition For two positive real numbers ''x'', ''y'' the Stolarsky Mean is defined as: : \begin S_p(x,y) & = \lim_ \left(\right)^ \\0pt& = \begin x & \textx=y \\ \left(\right)^ & \text \end \end Derivation It is derived from the mean value theorem, which states that a secant line, cutting the graph of a differentiable function f at ( x, f(x) ) and ( y, f(y) ), has the same slope as a line tangent to the graph at some point \xi in the interval ,y/math>. : \exists \xi\in ,y f'(\xi) = \frac The Stolarsky mean is obtained by : \xi = f'^\left(\frac\right) when choosing f(x) = x^p. Special cases *\lim_ S_p(x,y) is the minimum. *S_(x,y) is the geometric mean. *\lim_ S_p(x,y) is the logarithmic mean. It can be obtained from the mean value theorem by choosing f(x) = \ln x. *S_(x,y) is the power mean with exponent \frac. *\lim_ S_p(x,y) is the i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimum
In mathematical analysis, the maxima and minima (the respective plurals of maximum and minimum) of a function, known collectively as extrema (the plural of extremum), are the largest and smallest value of the function, either within a given range (the ''local'' or ''relative'' extrema), or on the entire domain (the ''global'' or ''absolute'' extrema). Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions. As defined in set theory, the maximum and minimum of a set are the greatest and least elements in the set, respectively. Unbounded infinite sets, such as the set of real numbers, have no minimum or maximum. Definition A real-valued function ''f'' defined on a domain ''X'' has a global (or absolute) maximum point at ''x''∗, if for all ''x'' in ''X''. Similarly, the function has a global (or absolute) minimum point at ''x''∗, if for all ''x'' in ''X''. The value of the function at a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable. Derivatives can be generalized to functions of several real variables. In this generalization, the derivativ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Value Theorem For Divided Differences
In mathematical analysis, the mean value theorem for divided differences generalizes the mean value theorem to higher derivatives. Statement of the theorem For any ''n'' + 1 pairwise distinct points ''x''0, ..., ''x''''n'' in the domain of an ''n''-times differentiable function ''f'' there exists an interior point : \xi \in (\min\,\max\) \, where the ''n''th derivative of ''f'' equals ''n'' ! times the ''n''th divided difference at these points: : f _0,\dots,x_n= \frac. For ''n'' = 1, that is two function points, one obtains the simple mean value theorem. Proof Let P be the Lagrange interpolation polynomial for ''f'' at ''x''0, ..., ''x''''n''. Then it follows from the Newton form of P that the highest term of P is f _0,\dots,x_nx-x_)\dots(x-x_1)(x-x_0). Let g be the remainder of the interpolation, defined by g = f - P. Then g has n+1 zeros: ''x''0, ..., ''x''''n''. By applying Rolle's theorem first to g, then to g', a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum
In mathematical analysis, the maxima and minima (the respective plurals of maximum and minimum) of a function, known collectively as extrema (the plural of extremum), are the largest and smallest value of the function, either within a given range (the ''local'' or ''relative'' extrema), or on the entire domain (the ''global'' or ''absolute'' extrema). Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions. As defined in set theory, the maximum and minimum of a set are the greatest and least elements in the set, respectively. Unbounded infinite sets, such as the set of real numbers, have no minimum or maximum. Definition A real-valued function ''f'' defined on a domain ''X'' has a global (or absolute) maximum point at ''x''∗, if for all ''x'' in ''X''. Similarly, the function has a global (or absolute) minimum point at ''x''∗, if for all ''x'' in ''X''. The value of the function at a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Mean
In mathematics and its applications, the root mean square of a set of numbers x_i (abbreviated as RMS, or rms and denoted in formulas as either x_\mathrm or \mathrm_x) is defined as the square root of the mean square (the arithmetic mean of the squares) of the set. The RMS is also known as the quadratic mean (denoted M_2) and is a particular case of the generalized mean. The RMS of a continuously varying function (denoted f_\mathrm) can be defined in terms of an integral of the squares of the instantaneous values during a cycle. For alternating electric current, RMS is equal to the value of the constant direct current that would produce the same power dissipation in a resistive load. In estimation theory, the root-mean-square deviation of an estimator is a measure of the imperfection of the fit of the estimator to the data. Definition The RMS value of a set of values (or a continuous-time waveform) is the square root of the arithmetic mean of the squares of the values, or t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic Mean
In mathematics and statistics, the arithmetic mean ( ) or arithmetic average, or just the ''mean'' or the ''average'' (when the context is clear), is the sum of a collection of numbers divided by the count of numbers in the collection. The collection is often a set of results of an experiment or an observational study, or frequently a set of results from a survey. The term "arithmetic mean" is preferred in some contexts in mathematics and statistics, because it helps distinguish it from other means, such as the geometric mean and the harmonic mean. In addition to mathematics and statistics, the arithmetic mean is used frequently in many diverse fields such as economics, anthropology and history, and it is used in almost every academic field to some extent. For example, per capita income is the arithmetic average income of a nation's population. While the arithmetic mean is often used to report central tendencies, it is not a robust statistic, meaning that it is greatly influe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identric Mean
The identric mean of two positive real numbers ''x'', ''y'' is defined as: : \begin I(x,y) &= \frac\cdot \lim_ \sqrt xi-\eta\\ pt&= \lim_ \exp\left(\frac-1\right) \\ pt&= \begin x & \textx=y \\ pt\frac \sqrt -y& \text \end \end It can be derived from the mean value theorem by considering the secant of the graph of the function x \mapsto x\cdot \ln x. It can be generalized to more variables according by the mean value theorem for divided differences. The identric mean is a special case of the Stolarsky mean. See also * Mean * Logarithmic mean In mathematics, the logarithmic mean is a function of two non-negative numbers which is equal to their difference divided by the logarithm of their quotient. This calculation is applicable in engineering problems involving heat and mass trans ... References {{DEFAULTSORT:Identric Mean Means ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Mean
Power most often refers to: * Power (physics), meaning "rate of doing work" ** Engine power, the power put out by an engine ** Electric power * Power (social and political), the ability to influence people or events ** Abusive power Power may also refer to: Mathematics, science and technology Computing * IBM POWER (software), an IBM operating system enhancement package * IBM POWER architecture, a RISC instruction set architecture * Power ISA, a RISC instruction set architecture derived from PowerPC * IBM Power microprocessors, made by IBM, which implement those RISC architectures * Power.org, a predecessor to the OpenPOWER Foundation * SGI POWER Challenge, a line of SGI supercomputers Mathematics * Exponentiation, "''x'' to the power of ''y''" * Power function * Power of a point * Statistical power Physics * Magnification, the factor by which an optical system enlarges an image * Optical power, the degree to which a lens converges or diverges light Social sciences and politi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Mean
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a set of numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean is defined as the th root of the product of numbers, i.e., for a set of numbers , the geometric mean is defined as :\left(\prod_^n a_i\right)^\frac = \sqrt /math> or, equivalently, as the arithmetic mean in logscale: :\exp For instance, the geometric mean of two numbers, say 2 and 8, is just the square root of their product, that is, \sqrt = 4. As another example, the geometric mean of the three numbers 4, 1, and 1/32 is the cube root of their product (1/8), which is 1/2, that is, \sqrt = 1/2. The geometric mean applies only to positive numbers. The geometric mean is often used for a set of numbers whose values are meant to be multiplied together or are exponential in nature, such as a set of growth figures: values of the human population or inter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interval (mathematics)
In mathematics, a (real) interval is a set of real numbers that contains all real numbers lying between any two numbers of the set. For example, the set of numbers satisfying is an interval which contains , , and all numbers in between. Other examples of intervals are the set of numbers such that , the set of all real numbers \R, the set of nonnegative real numbers, the set of positive real numbers, the empty set, and any singleton (set of one element). Real intervals play an important role in the theory of integration, because they are the simplest sets whose "length" (or "measure" or "size") is easy to define. The concept of measure can then be extended to more complicated sets of real numbers, leading to the Borel measure and eventually to the Lebesgue measure. Intervals are central to interval arithmetic, a general numerical computing technique that automatically provides guaranteed enclosures for arbitrary formulas, even in the presence of uncertainties, mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithmic Mean
In mathematics, the logarithmic mean is a function of two non-negative numbers which is equal to their difference divided by the logarithm of their quotient. This calculation is applicable in engineering problems involving heat and mass transfer. Definition The logarithmic mean is defined as: :\begin M_\text(x, y) &= \lim_ \frac \\ pt &= \begin x & \textx = y ,\\ \frac & \text \end \end for the positive numbers x, y. Inequalities The logarithmic mean of two numbers is smaller than the arithmetic mean and the generalized mean with exponent one-third but larger than the geometric mean, unless the numbers are the same, in which case all three means are equal to the numbers. : \sqrt \leq \frac\leq \left(\frac2\right)^3 \leq \frac \qquad \text x > 0 \text y > 0. Toyesh Prakash Sharma generalizes the arithmetic logarithmic geometric mean inequality for any n belongs to the whole number as : \sqrt (\ln(\sqrt))^ (\ln(\sqrt)+n)\leq \frac\leq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |