|
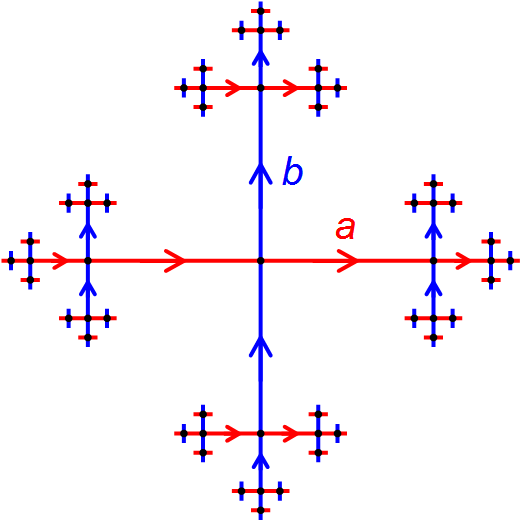
Quasi-isometry
In mathematics, a quasi-isometry is a function between two metric spaces that respects large-scale geometry of these spaces and ignores their small-scale details. Two metric spaces are quasi-isometric if there exists a quasi-isometry between them. The property of being quasi-isometric behaves like an equivalence relation on the class of metric spaces. The concept of quasi-isometry is especially important in geometric group theory, following the work of Gromov. Definition Suppose that f is a (not necessarily continuous) function from one metric space (M_1,d_1) to a second metric space (M_2,d_2). Then f is called a ''quasi-isometry'' from (M_1,d_1) to (M_2,d_2) if there exist constants A\ge 1, B\ge 0, and C\ge 0 such that the following two properties both hold:P. de la Harpe, ''Topics in geometric group theory''. Chicago Lectures in Mathematics. University of Chicago Press, Chicago, IL, 2000. #For every two points x and y in M_1, the distance between their images is up to the addit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Group Theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such group (mathematics), groups and topology, topological and geometry, geometric properties of spaces on which these groups Group action (mathematics), act (that is, when the groups in question are realized as geometric symmetries or continuous transformations of some spaces). Another important idea in geometric group theory is to consider finitely generated groups themselves as geometric objects. This is usually done by studying the Cayley graphs of groups, which, in addition to the graph (discrete mathematics), graph structure, are endowed with the structure of a metric space, given by the so-called word metric. Geometric group theory, as a distinct area, is relatively new, and became a clearly identifiable branch of mathematics in the late 1980s and early 1990s. Geometric group theory closely interacts with low-dimens ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric Space
In mathematics, a metric space is a set together with a notion of ''distance'' between its elements, usually called points. The distance is measured by a function called a metric or distance function. Metric spaces are the most general setting for studying many of the concepts of mathematical analysis and geometry. The most familiar example of a metric space is 3-dimensional Euclidean space with its usual notion of distance. Other well-known examples are a sphere equipped with the angular distance and the hyperbolic plane. A metric may correspond to a metaphorical, rather than physical, notion of distance: for example, the set of 100-character Unicode strings can be equipped with the Hamming distance, which measures the number of characters that need to be changed to get from one string to another. Since they are very general, metric spaces are a tool used in many different branches of mathematics. Many types of mathematical objects have a natural notion of distance and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
δ-hyperbolic Space
In mathematics, a hyperbolic metric space is a metric space satisfying certain metric relations (depending quantitatively on a nonnegative real number δ) between points. The definition, introduced by Mikhael Gromov, generalizes the metric properties of classical hyperbolic geometry and of trees. Hyperbolicity is a large-scale property, and is very useful to the study of certain infinite groups called Gromov-hyperbolic groups. Definitions In this paragraph we give various definitions of a \delta-hyperbolic space. A metric space is said to be (Gromov-) hyperbolic if it is \delta-hyperbolic for some \delta > 0. Definition using the Gromov product Let (X,d) be a metric space. The Gromov product of two points y, z \in X with respect to a third one x \in X is defined by the formula: :(y,z)_x = \frac 1 2 \left( d(x, y) + d(x, z) - d(y, z) \right). Gromov's definition of a hyperbolic metric space is then as follows: X is \delta-hyperbolic if and only if all x,y,z,w \in X satisfy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Švarc–Milnor Lemma
In the mathematical subject of geometric group theory, the Švarc–Milnor lemma (sometimes also called Milnor–Švarc lemma, with both variants also sometimes spelling Švarc as Schwarz) is a statement which says that a group G, equipped with a "nice" discrete action, discrete isometric Group action (mathematics), action on a metric space X, is Quasi-isometry, quasi-isometric to X. This result goes back, in different form, before the notion of quasi-isometry was formally introduced, to the work of Albert Schwarz, Albert S. Schwarz (1955) and John Milnor (1968). Pierre de la Harpe called the Švarc–Milnor lemma ``the ''fundamental observation in geometric group theory''"Pierre de la Harpe, ''Topics in geometric group theory'. Chicago Lectures in Mathematics. University of Chicago Press, Chicago, IL, 2000. ; p. 87 because of its importance for the subject. Occasionally the name "fundamental observation in geometric group theory" is now used for this statement, instead of ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gromov's Theorem On Groups Of Polynomial Growth
In geometric group theory, Gromov's theorem on groups of polynomial growth, first proved by Mikhail Gromov (mathematician), Mikhail Gromov, characterizes finitely generated Group (mathematics), groups of ''polynomial'' growth, as those groups which have nilpotent group, nilpotent subgroups of finite index of a subgroup, index. Statement The Growth rate (group theory), growth rate of a group is a well-defined notion from asymptotic analysis. To say that a finitely generated group has polynomial growth means the number of elements of length (relative to a symmetric generating set) at most ''n'' is bounded above by a polynomial function ''p''(''n''). The ''order of growth'' is then the least degree of any such polynomial function ''p''. A nilpotent group ''G'' is a group with a lower central series terminating in the identity subgroup. Gromov's theorem states that a finitely generated group has polynomial growth if and only if it has a nilpotent subgroup that is of finite index. Gro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Invariant (mathematics)
In mathematics, an invariant is a property of a mathematical object (or a class of mathematical objects) which remains unchanged after operations or transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used. For example, the area of a triangle is an invariant with respect to isometries of the Euclidean plane. The phrases "invariant under" and "invariant to" a transformation are both used. More generally, an invariant with respect to an equivalence relation is a property that is constant on each equivalence class. Invariants are used in diverse areas of mathematics such as geometry, topology, algebra and discrete mathematics. Some important classes of transformations are defined by an invariant they leave unchanged. For example, conformal maps are defined as transformations of the plane that preserve angles. The discovery of invariants is an important ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Virtually Nilpotent
In mathematics, especially in the area of abstract algebra that studies infinite groups, the adverb virtually is used to modify a property so that it need only hold for a subgroup of finite index. Given a property P, the group ''G'' is said to be ''virtually P'' if there is a finite index subgroup H \le G such that ''H'' has property P. Common uses for this would be when P is abelian, nilpotent, solvable or free. For example, virtually solvable groups are one of the two alternatives in the Tits alternative, while Gromov's theorem states that the finitely generated groups with polynomial growth are precisely the finitely generated virtually nilpotent groups. This terminology is also used when P is just another group. That is, if ''G'' and ''H'' are groups then ''G'' is ''virtually'' ''H'' if ''G'' has a subgroup ''K'' of finite index in ''G'' such that ''K'' is isomorphic to ''H''. In particular, a group is virtually trivial if and only if it is finite. Two groups are v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Automatic Group
In mathematics, an automatic group is a finitely generated group equipped with several finite-state automata. These automata represent the Cayley graph of the group. That is, they can tell if a given word representation of a group element is in a "canonical form" and can tell if two elements given in canonical words differ by a generator. More precisely, let ''G'' be a group and ''A'' be a finite set of generators. Then an ''automatic structure'' of ''G'' with respect to ''A'' is a set of finite-state automata: * the ''word-acceptor'', which accepts for every element of ''G'' at least one word in A^\ast representing it; *''multipliers'', one for each a \in A \cup \, which accept a pair (''w''1, ''w''2), for words ''w''''i'' accepted by the word-acceptor, precisely when w_1 a = w_2 in ''G''. The property of being automatic does not depend on the set of generators. Properties Automatic groups have word problem solvable in quadratic time. More strongly, a given word can actual ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biautomatic Group
In mathematics, an automatic group is a finitely generated group equipped with several finite-state automata. These automata represent the Cayley graph of the group. That is, they can tell if a given word representation of a group element is in a "canonical form" and can tell if two elements given in canonical words differ by a generator. More precisely, let ''G'' be a group and ''A'' be a finite set of generators. Then an ''automatic structure'' of ''G'' with respect to ''A'' is a set of finite-state automata: * the ''word-acceptor'', which accepts for every element of ''G'' at least one word in A^\ast representing it; *''multipliers'', one for each a \in A \cup \, which accept a pair (''w''1, ''w''2), for words ''w''''i'' accepted by the word-acceptor, precisely when w_1 a = w_2 in ''G''. The property of being automatic does not depend on the set of generators. Properties Automatic groups have word problem solvable in quadratic time. More strongly, a given word can actua ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Word Problem For Groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group ''G'' is the algorithmic problem of deciding whether two words in the generators represent the same element. More precisely, if ''A'' is a finite set of generators for ''G'' then the word problem is the membership problem for the formal language of all words in ''A'' and a formal set of inverses that map to the identity under the natural map from the free monoid with involution on ''A'' to the group ''G''. If ''B'' is another finite generating set for ''G'', then the word problem over the generating set ''B'' is equivalent to the word problem over the generating set ''A''. Thus one can speak unambiguously of the decidability of the word problem for the finitely generated group ''G''. The related but different uniform word problem for a class ''K'' of recursively presented groups is the algorithmic problem of deciding, given as input a pres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mostow Rigidity Theorem
Mostow may refer to: People * George Mostow (1923–2017), American mathematician ** Mostow rigidity theorem * Jonathan Mostow Jonathan Mostow (born November 28, 1961) is an American film director, screenwriter, and producer. He has directed films such as ''Breakdown (1997 film), Breakdown'', ''U-571 (film), U-571'', ''Terminator 3: Rise of the Machines'', and ''Surroga ... (born 1961), American movie and television director Places * Mostów, a village in Poland {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |