|
≈Ývarc‚ÄìMilnor Lemma
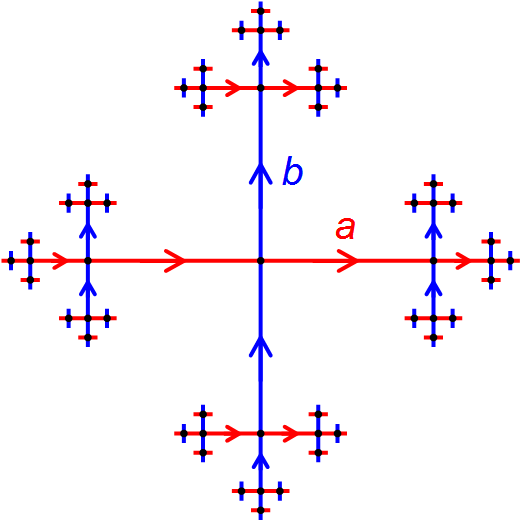
In the mathematical subject of geometric group theory, the ≈Ývarc‚ÄìMilnor lemma (sometimes also called Milnor‚Äì≈Ývarc lemma, with both variants also sometimes spelling ≈Ývarc as Schwarz) is a statement which says that a group G, equipped with a "nice" discrete isometric action on a metric space X, is quasi-isometric to X. This result goes back, in different form, before the notion of quasi-isometry was formally introduced, to the work of Albert S. Schwarz (1955) and John Milnor (1968). Pierre de la Harpe called the ≈Ývarc‚ÄìMilnor lemma "the ''fundamental observation in geometric group theory''"Pierre de la Harpe, Topics in geometric group theory'. Chicago Lectures in Mathematics. University of Chicago Press, Chicago, IL, 2000. ; p. 87 because of its importance for the subject. Occasionally the name "fundamental observation in geometric group theory" is now used for this statement, instead of calling it the ≈Ývarc‚ÄìMilnor lemma; see, for example, Theorem 8.2 in the book ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Geometric Group Theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups can act non-trivially (that is, when the groups in question are realized as geometric symmetries or continuous transformations of some spaces). Another important idea in geometric group theory is to consider finitely generated groups themselves as geometric objects. This is usually done by studying the Cayley graphs of groups, which, in addition to the graph structure, are endowed with the structure of a metric space, given by the so-called word metric. Geometric group theory, as a distinct area, is relatively new, and became a clearly identifiable branch of mathematics in the late 1980s and early 1990s. Geometric group theory closely interacts with low-dimensional topology, hyperbolic geometry, algebraic topology, computational group ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cocompact Group Action
In mathematics, an action of a group ''G'' on a topological space ''X'' is cocompact if the quotient space ''X''/''G'' is a compact space. If ''X'' is locally compact In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space. More precisely, it is a topological space in which e ..., then an equivalent condition is that there is a compact subset ''K'' of ''X'' such that the image of ''K'' under the action of ''G'' covers ''X''. It is sometimes referred to as ''mpact'', a tongue-in-cheek reference to dual notions where prefixing with "co-" twice would "cancel out". References * Group actions {{topology-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Horoball
In hyperbolic geometry, a horosphere (or parasphere) is a specific hypersurface in hyperbolic ''n''-space. It is the boundary of a horoball, the limit of a sequence of increasing balls sharing (on one side) a tangent hyperplane and its point of tangency. For ''n'' = 2 a horosphere is called a horocycle. A horosphere can also be described as the limit of the hyperspheres that share a tangent hyperplane at a given point, as their radii go towards infinity. In Euclidean geometry, such a "hypersphere of infinite radius" would be a hyperplane, but in hyperbolic geometry it is a horosphere (a curved surface). History The concept has its roots in a notion expressed by F. L. Wachter in 1816 in a letter to his teacher Gauss. Noting that in Euclidean geometry the limit of a sphere as its radius tends to infinity is a plane, Wachter affirmed that even if the fifth postulate were false, there would nevertheless be a geometry on the surface identical with that of the ordinary plane. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lattice (discrete Subgroup)
In Lie theory and related areas of mathematics, a lattice in a locally compact group is a discrete subgroup with the property that the quotient space has finite invariant measure. In the special case of subgroups of R''n'', this amounts to the usual geometric notion of a lattice as a periodic subset of points, and both the algebraic structure of lattices and the geometry of the space of all lattices are relatively well understood. The theory is particularly rich for lattices in semisimple Lie groups or more generally in semisimple algebraic groups over local fields. In particular there is a wealth of rigidity results in this setting, and a celebrated theorem of Grigory Margulis states that in most cases all lattices are obtained as arithmetic groups. Lattices are also well-studied in some other classes of groups, in particular groups associated to Kac–Moody algebras and automorphisms groups of regular trees (the latter are known as ''tree lattices''). Lattices a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lie Group
In mathematics, a Lie group (pronounced ) is a group (mathematics), group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the additional properties it must have to be thought of as a "transformation" in the abstract sense, for instance multiplication and the taking of inverses (to allow division), or equivalently, the concept of addition and subtraction. Combining these two ideas, one obtains a continuous group where multiplying points and their inverses is continuous. If the multiplication and taking of inverses are smoothness, smooth (differentiable) as well, one obtains a Lie group. Lie groups provide a natural model for the concept of continuous symmetry, a celebrated example of which is the circle group. Rotating a circle is an example of a continuous symmetry. For an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |