|
Markov Chain Monte Carlo
In statistics, Markov chain Monte Carlo (MCMC) methods comprise a class of algorithms for sampling from a probability distribution. By constructing a Markov chain that has the desired distribution as its equilibrium distribution, one can obtain a sample of the desired distribution by recording states from the chain. The more steps that are included, the more closely the distribution of the sample matches the actual desired distribution. Various algorithms exist for constructing chains, including the Metropolis–Hastings algorithm. Application domains MCMC methods are primarily used for calculating numerical approximations of multi-dimensional integrals, for example in Bayesian statistics, computational physics, computational biology and computational linguistics. In Bayesian statistics, the recent development of MCMC methods has made it possible to compute large hierarchical models that require integrations over hundreds to thousands of unknown parameters. In rare even ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its population mean or sample mean. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. Variance has a central role in statistics, where some ideas that use it include descriptive statistics, statistical inference, hypothesis testing, goodness of fit, and Monte Carlo sampling. Variance is an important tool in the sciences, where statistical analysis of data is common. The variance is the square of the standard deviation, the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviation; for e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
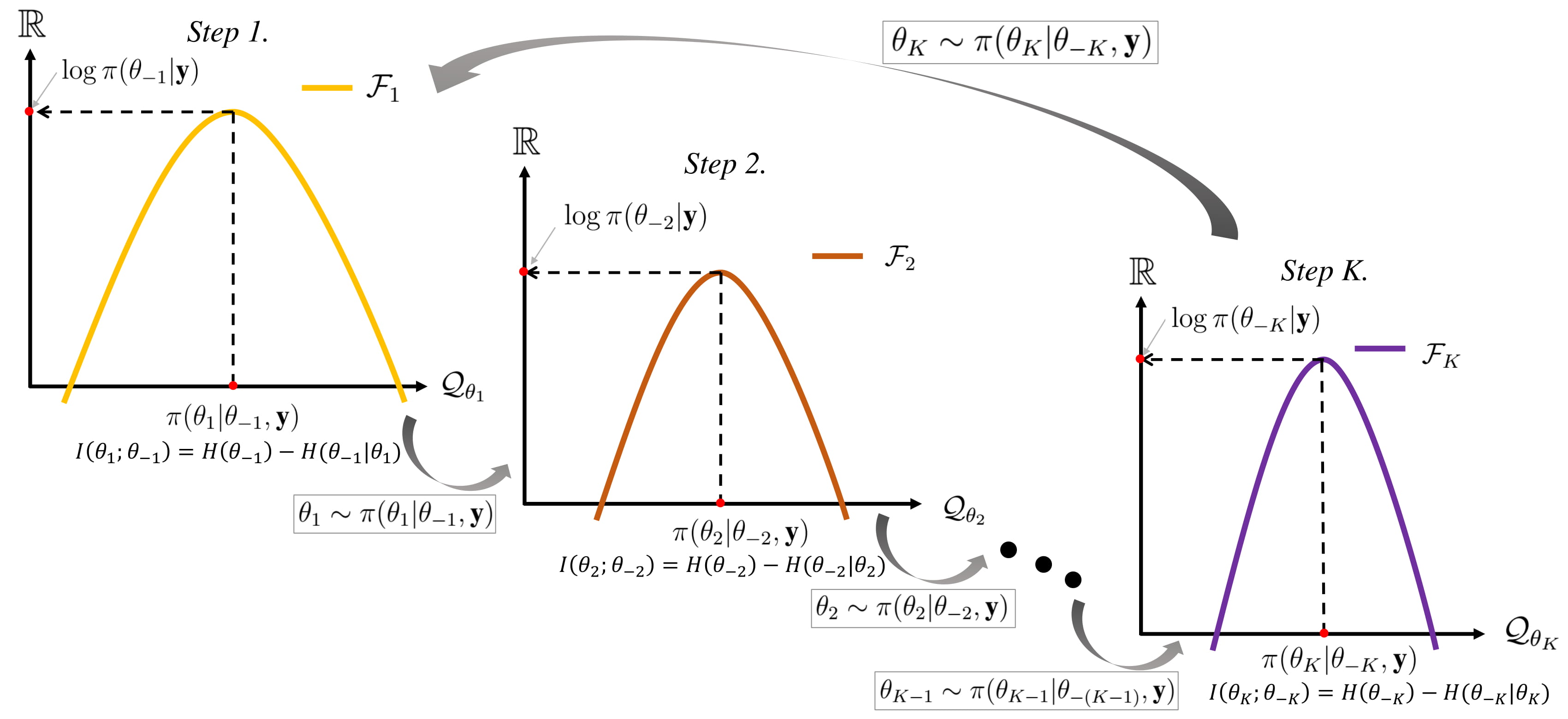
Gibbs Sampling
In statistics, Gibbs sampling or a Gibbs sampler is a Markov chain Monte Carlo (MCMC) algorithm for obtaining a sequence of observations which are approximated from a specified multivariate probability distribution, when direct sampling is difficult. This sequence can be used to approximate the joint distribution (e.g., to generate a histogram of the distribution); to approximate the marginal distribution of one of the variables, or some subset of the variables (for example, the unknown parameters or latent variables); or to compute an integral (such as the expected value of one of the variables). Typically, some of the variables correspond to observations whose values are known, and hence do not need to be sampled. Gibbs sampling is commonly used as a means of statistical inference, especially Bayesian inference. It is a randomized algorithm (i.e. an algorithm that makes use of random numbers), and is an alternative to deterministic algorithms for statistical inferenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wang And Landau Algorithm
The Wang and Landau algorithm, proposed by Fugao Wang and David P. Landau, is a Monte Carlo method designed to estimate the density of states of a system. The method performs a non-Markovian random walk to build the density of states by quickly visiting all the available energy spectrum. The Wang and Landau algorithm is an important method to obtain the density of states required to perform a multicanonical simulation. The Wang–Landau algorithm can be applied to any system which is characterized by a cost (or energy) function. For instance, it has been applied to the solution of numerical integrals and the folding of proteins. The Wang–Landau sampling is related to the metadynamics algorithm.Christoph Junghans, Danny Perez, and Thomas Vogel. "Molecular Dynamics in the Multicanonical Ensemble: Equivalence of Wang–Landau Sampling, Statistical Temperature Molecular Dynamics, and Metadynamics." Journal of Chemical Theory and Computation 10.5 (2014): 1843-1847. doibr>10.1021/ct5 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian Monte Carlo
The Hamiltonian Monte Carlo algorithm (originally known as hybrid Monte Carlo) is a Markov chain Monte Carlo method for obtaining a sequence of random samples which converge to being distributed according to a target probability distribution for which direct sampling is difficult. This sequence can be used to estimate integrals with respect to the target distribution (expected values). Hamiltonian Monte Carlo corresponds to an instance of the Metropolis–Hastings algorithm, with a Hamiltonian dynamics evolution simulated using a time-reversible and volume-preserving numerical integrator (typically the leapfrog integrator) to propose a move to a new point in the state space. Compared to using a Gaussian random walk proposal distribution in the Metropolis–Hastings algorithm, Hamiltonian Monte Carlo reduces the correlation between successive sampled states by proposing moves to distant states which maintain a high probability of acceptance due to the approximate energy conserving ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curse Of Dimensionality
The curse of dimensionality refers to various phenomena that arise when analyzing and organizing data in high-dimensional spaces that do not occur in low-dimensional settings such as the three-dimensional physical space of everyday experience. The expression was coined by Richard E. Bellman when considering problems in dynamic programming. Dimensionally cursed phenomena occur in domains such as numerical analysis, sampling, combinatorics, machine learning, data mining and databases. The common theme of these problems is that when the dimensionality increases, the volume of the space increases so fast that the available data become sparse. In order to obtain a reliable result, the amount of data needed often grows exponentially with the dimensionality. Also, organizing and searching data often relies on detecting areas where objects form groups with similar properties; in high dimensional data, however, all objects appear to be sparse and dissimilar in many ways, which prevents co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Chains
A Markov chain or Markov process is a stochastic process, stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, this may be thought of as, "What happens next depends only on the state of affairs ''now''." A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). A continuous-time process is called a continuous-time Markov chain (CTMC). It is named after the Russian mathematician Andrey Markov. Markov chains have many applications as statistical models of real-world processes, such as studying cruise control, cruise control systems in motor vehicles, queues or lines of customers arriving at an airport, currency exchange rates and animal population dynamics. Markov processes are the basis for general stochastic simulation methods known as Markov chain Monte Carlo, which are used for simulating sampl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Chain Central Limit Theorem
In the mathematical theory of random processes, the Markov chain central limit theorem has a conclusion somewhat similar in form to that of the classic central limit theorem (CLT) of probability theory, but the quantity in the role taken by the variance in the classic CLT has a more complicated definition. See also the general form of Bienaymé's identity. Statement Suppose that: * the sequence X_1,X_2,X_3,\ldots of random elements of some set is a Markov chain that has a stationary probability distribution; and * the initial distribution of the process, i.e. the distribution of X_1, is the stationary distribution, so that X_1,X_2,X_3,\ldots are identically distributed. In the classic central limit theorem these random variables would be assumed to be independent, but here we have only the weaker assumption that the process has the Markov property; and * g is some (measurable) real-valued function for which \operatorname(g(X_1)) <+\infty. Now let : |
Autocorrelation
Autocorrelation, sometimes known as serial correlation in the discrete time case, is the correlation of a signal with a delayed copy of itself as a function of delay. Informally, it is the similarity between observations of a random variable as a function of the time lag between them. The analysis of autocorrelation is a mathematical tool for finding repeating patterns, such as the presence of a periodic signal obscured by noise, or identifying the missing fundamental frequency in a signal implied by its harmonic frequencies. It is often used in signal processing for analyzing functions or series of values, such as time domain signals. Different fields of study define autocorrelation differently, and not all of these definitions are equivalent. In some fields, the term is used interchangeably with autocovariance. Unit root processes, trend-stationary processes, autoregressive processes, and moving average processes are specific forms of processes with autocorrelation. A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistically Independent
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two events are independent, statistically independent, or stochastically independent if, informally speaking, the occurrence of one does not affect the probability of occurrence of the other or, equivalently, does not affect the odds. Similarly, two random variables are independent if the realization of one does not affect the probability distribution of the other. When dealing with collections of more than two events, two notions of independence need to be distinguished. The events are called pairwise independent if any two events in the collection are independent of each other, while mutual independence (or collective independence) of events means, informally speaking, that each event is independent of any combination of other events in the collection. A similar notion exists for collections of random variables. Mutual independence implies pairwise independence, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monte Carlo Integration
In mathematics, Monte Carlo integration is a technique for numerical integration using random numbers. It is a particular Monte Carlo method that numerically computes a definite integral. While other algorithms usually evaluate the integrand at a regular grid, Monte Carlo randomly chooses points at which the integrand is evaluated. This method is particularly useful for higher-dimensional integrals. There are different methods to perform a Monte Carlo integration, such as uniform sampling, stratified sampling, importance sampling, sequential Monte Carlo (also known as a particle filter), and mean-field particle methods. Overview In numerical integration, methods such as the trapezoidal rule use a deterministic approach. Monte Carlo integration, on the other hand, employs a non-deterministic approach: each realization provides a different outcome. In Monte Carlo, the final outcome is an approximation of the correct value with respective error bars, and the correct value is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monte Carlo Method
Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to use other approaches. Monte Carlo methods are mainly used in three problem classes: optimization, numerical integration, and generating draws from a probability distribution. In physics-related problems, Monte Carlo methods are useful for simulating systems with many coupled degrees of freedom, such as fluids, disordered materials, strongly coupled solids, and cellular structures (see cellular Potts model, interacting particle systems, McKean–Vlasov processes, kinetic models of gases). Other examples include modeling phenomena with significant uncertainty in inputs such as the calculation of ris ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |